第二章 相交线与平行线(单元复习课件) 共17张PPT
文档属性
| 名称 | 第二章 相交线与平行线(单元复习课件) 共17张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 492.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第二章 相交线与平行线
章末复习
七
下
数
学
2020
回顾 & 思考
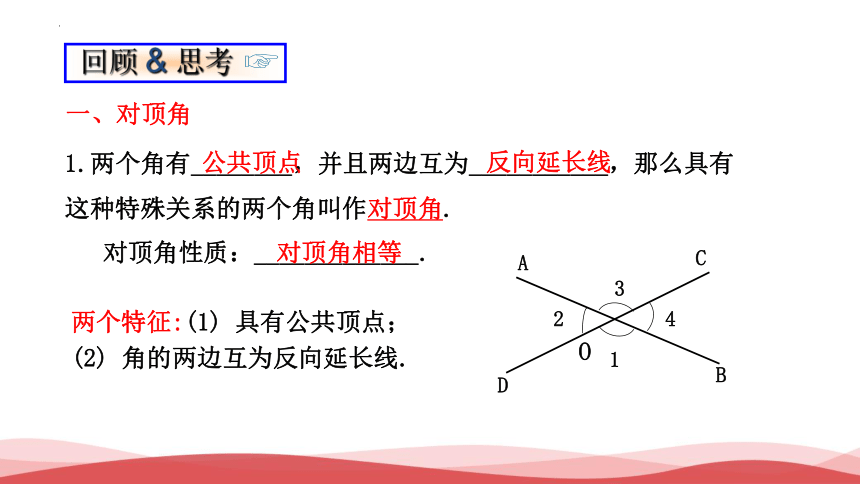
一、对顶角
1.两个角有________,并且两边互为___________,那么具有这种特殊关系的两个角叫作对顶角.
对顶角性质:_____________.
A
O
C
B
D
1
3
2
4
公共顶点
反向延长线
对顶角相等
两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线.
2.补角:如果两个角的和是180°,那么称这两个角互为补角.
3.余角:如果两个角的和是90°,那么称这两个角互为余角.
二、垂线
当两条直线相交所成的四个角中,有一个角是_____时,这两条直线互相垂直,其中一条直线叫另一条直线的______,它们的交点叫______.
1.垂线的定义
2.经过直线上或直线外一点,_____________一条直线与已知直线垂直.
4.直线外一点到这条直线的垂线段的______,叫作点到
直线的距离.
3.直线外一点与直线上各点的所有连线中,_______最短.
有且只有
垂线段
距离
直角
垂线
垂足
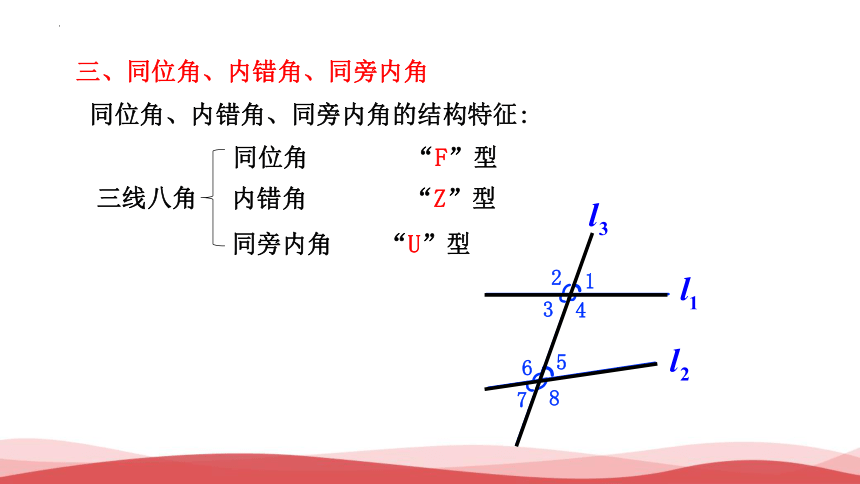
同位角、内错角、同旁内角的结构特征:
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
三、同位角、内错角、同旁内角
三线八角
四、平行线
1.在同一平面内,_______的两条直线叫作平行线.
3.平行于同一条直线的两条直线_______.
2.经过直线外一点,________一条直线与已知直线平行.
4.平行线的判定与性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
不相交
有且只有
平行
探索&交流
例1.下列说法正确的是( )
A.不相交的两条直线是平行线
B.在同一平面内,不相交的两条射线是平行线
C.在同一平面内,两条直线不相交就重合
D.在同一平面内,没有公共点的两条直线是平行线
D
典例精析
探索&交流
典例精析
例2.同一平面内,下列说法:①过两点有且只有一条直线;②两直线不平行,则一定相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且仅有一条直线与已知直线平行,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
D
探索&交流
典例精析
例3.如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
因为AB⊥CD,所以∠AOC=90°.
因为∠AOE=65°,
所以∠COE=25°.
又因为∠COE=∠DOF(对顶角相等),
所以∠DOF=25°.
探索&交流
典例精析
例4.如图,∠1=∠2,AC平分∠DAB,DC∥AB吗?为什么?
解:DC∥AB.理由:
因为由AC平分∠DAB,故∠1=∠CAB,又∠1=∠2,所以∠2=∠CAB.因而AB∥CD(内错角相等,两直线平行).
典例精析
例5.如图所示, 交于点O, ∠1=∠2,∠3:∠1=8:1, 求∠4的度数.
4
1
2
3
解:设∠1的度数为x°,则∠2的度数为x°,
则∠3的度数为8x°,根据题意可得
x°+x°+8x°=180°,解得x=18.
即∠1=∠2=18°,
而∠4=∠1+∠2(对顶角相等).
故∠4=36°.
探索&交流
典例精析
例6.如图,AB∥CD,∠BAE=30°,∠ECD=60°,那么∠AEC度数为多少?
解:如图,过E作EF∥AB,
则∠1=∠A=30°;因为AB∥CD,
所以EF∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),
所以∠2=∠C=60°,
那么∠AEC=∠1+∠2=30°+60°=90°.
随堂练习
练习&巩固
1.如图,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D= ( )
A.75° B.45° C.30° D.15°
D
练习&巩固
2.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点A到BC的距离是______,点B到AC的距离是______ ,A、B两点的距离是______ ,点C到AB的距离是______.
6cm
8cm
10cm
4.8cm
练习&巩固
3.如图,直线L1∥L2,则∠α为( )
A.150° B.140° C.130° D.120°
D
4.如图所示,修一条路将B村庄与A村庄及公路MN连
起来,怎样修才能使所修的公路最短?画出线路图,并说明理由.
解:连接AB,作BC⊥MN,C是垂足,线段AB和BC就是符合题意的线路图.因为从A到B,线段AB最短,
从B到MN,垂线段BC最短,所以AB+BC最短.
练习&巩固
5.如图,已知△ABC,AD⊥BC于D,E为AB上一点,EF⊥BC于F,DG//BA交CA于G.∠1与∠2相等吗?为什么?
解:∠1=∠2.理由:
因为AD⊥BC,FE⊥BC,
所以∠EFB=∠ADB=90°,所以EF//AD,
所以∠2=∠3,
因为DG//BA,所以∠3=∠1,所以∠1=∠2.
练习&巩固
第二章 相交线与平行线
章末复习
七
下
数
学
2020
回顾 & 思考
一、对顶角
1.两个角有________,并且两边互为___________,那么具有这种特殊关系的两个角叫作对顶角.
对顶角性质:_____________.
A
O
C
B
D
1
3
2
4
公共顶点
反向延长线
对顶角相等
两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线.
2.补角:如果两个角的和是180°,那么称这两个角互为补角.
3.余角:如果两个角的和是90°,那么称这两个角互为余角.
二、垂线
当两条直线相交所成的四个角中,有一个角是_____时,这两条直线互相垂直,其中一条直线叫另一条直线的______,它们的交点叫______.
1.垂线的定义
2.经过直线上或直线外一点,_____________一条直线与已知直线垂直.
4.直线外一点到这条直线的垂线段的______,叫作点到
直线的距离.
3.直线外一点与直线上各点的所有连线中,_______最短.
有且只有
垂线段
距离
直角
垂线
垂足
同位角、内错角、同旁内角的结构特征:
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
三、同位角、内错角、同旁内角
三线八角
四、平行线
1.在同一平面内,_______的两条直线叫作平行线.
3.平行于同一条直线的两条直线_______.
2.经过直线外一点,________一条直线与已知直线平行.
4.平行线的判定与性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
不相交
有且只有
平行
探索&交流
例1.下列说法正确的是( )
A.不相交的两条直线是平行线
B.在同一平面内,不相交的两条射线是平行线
C.在同一平面内,两条直线不相交就重合
D.在同一平面内,没有公共点的两条直线是平行线
D
典例精析
探索&交流
典例精析
例2.同一平面内,下列说法:①过两点有且只有一条直线;②两直线不平行,则一定相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且仅有一条直线与已知直线平行,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
D
探索&交流
典例精析
例3.如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
因为AB⊥CD,所以∠AOC=90°.
因为∠AOE=65°,
所以∠COE=25°.
又因为∠COE=∠DOF(对顶角相等),
所以∠DOF=25°.
探索&交流
典例精析
例4.如图,∠1=∠2,AC平分∠DAB,DC∥AB吗?为什么?
解:DC∥AB.理由:
因为由AC平分∠DAB,故∠1=∠CAB,又∠1=∠2,所以∠2=∠CAB.因而AB∥CD(内错角相等,两直线平行).
典例精析
例5.如图所示, 交于点O, ∠1=∠2,∠3:∠1=8:1, 求∠4的度数.
4
1
2
3
解:设∠1的度数为x°,则∠2的度数为x°,
则∠3的度数为8x°,根据题意可得
x°+x°+8x°=180°,解得x=18.
即∠1=∠2=18°,
而∠4=∠1+∠2(对顶角相等).
故∠4=36°.
探索&交流
典例精析
例6.如图,AB∥CD,∠BAE=30°,∠ECD=60°,那么∠AEC度数为多少?
解:如图,过E作EF∥AB,
则∠1=∠A=30°;因为AB∥CD,
所以EF∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),
所以∠2=∠C=60°,
那么∠AEC=∠1+∠2=30°+60°=90°.
随堂练习
练习&巩固
1.如图,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D= ( )
A.75° B.45° C.30° D.15°
D
练习&巩固
2.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点A到BC的距离是______,点B到AC的距离是______ ,A、B两点的距离是______ ,点C到AB的距离是______.
6cm
8cm
10cm
4.8cm
练习&巩固
3.如图,直线L1∥L2,则∠α为( )
A.150° B.140° C.130° D.120°
D
4.如图所示,修一条路将B村庄与A村庄及公路MN连
起来,怎样修才能使所修的公路最短?画出线路图,并说明理由.
解:连接AB,作BC⊥MN,C是垂足,线段AB和BC就是符合题意的线路图.因为从A到B,线段AB最短,
从B到MN,垂线段BC最短,所以AB+BC最短.
练习&巩固
5.如图,已知△ABC,AD⊥BC于D,E为AB上一点,EF⊥BC于F,DG//BA交CA于G.∠1与∠2相等吗?为什么?
解:∠1=∠2.理由:
因为AD⊥BC,FE⊥BC,
所以∠EFB=∠ADB=90°,所以EF//AD,
所以∠2=∠3,
因为DG//BA,所以∠3=∠1,所以∠1=∠2.
练习&巩固
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
