人教A版2024年高考数学难点专题必修二难点 立体几何初步1(含解析)
文档属性
| 名称 | 人教A版2024年高考数学难点专题必修二难点 立体几何初步1(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 15:08:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
必修二难点 立体几何初步1
一、单选题
1.一平面截球O得到半径为cm的圆面,球心到这个平面的距离是2cm,则球O的体积是
A.12π cm3 B.36π cm3 C.cm3 D.cm3
2.已知A,B是半径为的球面上的两点,过AB作互相垂直的两个平面,若球心到截该球所得两个截面距离平方之和为8,则线段AB的长度是
A. B.2 C. D.4
3.下列命题正确的是( )
A.有两个面互相平行,其余四个面都是等腰梯形的六面体为棱台
B.用一个平面去截棱锥,棱锥底面和截面之间的部分为棱台
C.棱锥是由一个底面为多边形,其余各面为具有公共顶点的三角形围成的几何体
D.一个正方形按不同方向平移所得几何体都是正方体
4.已知异面直线A.与b成80的角,p为空间一定点,则过点p与A.,b所成的角都是50的直线有且仅有( ).
A.1条 B.2条 C.3条 D.4条
5.已知为两两垂直的三条异面直线,过作平面α与直线垂直,则直线与平面的关系是( )
A.∥ B.∥或
C.或与不平行 D.
6.在正方体中,分别为的中点,则异面直线与所成角的大小为( )
A. B. C. D.
7.球缺是指一个球被平面截下的部分,截面为球缺的底面,垂直于截面的直径被截面截得的线段长为球缺的高,球缺曲面部分的面积(球冠面积)(为球的半径,为球缺的高).已知正三棱柱的顶点都在球的表面上,球的表面积为,该正三棱柱的体积为,若的边长为整数,则球被该正三棱柱上、下底面所在平面截掉两个球缺后剩余部分的表面积为( )
A. B. C. D.
8.如图,在三棱柱中,底面分别是棱的中点,点F在棱上,,则下列说法正确的是( )
A.设平面与平面的交线为l,则直线与l相交
B.在棱上存在点N,使得三棱锥的体积为
C.在棱上存在点P,使得
D.设点M在上,当时,平面平面
9.在四面体中,,,,,则该四面体的外接球的表面积为( )
A. B. C. D.
10.如图所示,直三棱柱的高为4,底面边长分别是5,12,13,当球与上底面三条棱都相切时球心到下底面距离为8,则球的体积为
A. B. C. D.
11.在矩形ABCD中,,,沿矩形对角线BD将折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当时,;②四面体ABCD的体积的最大值为;③在四面体ABCD中,BC与平面ABD所成角可能为;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为
A.①④ B.①② C.①②④ D.②③④
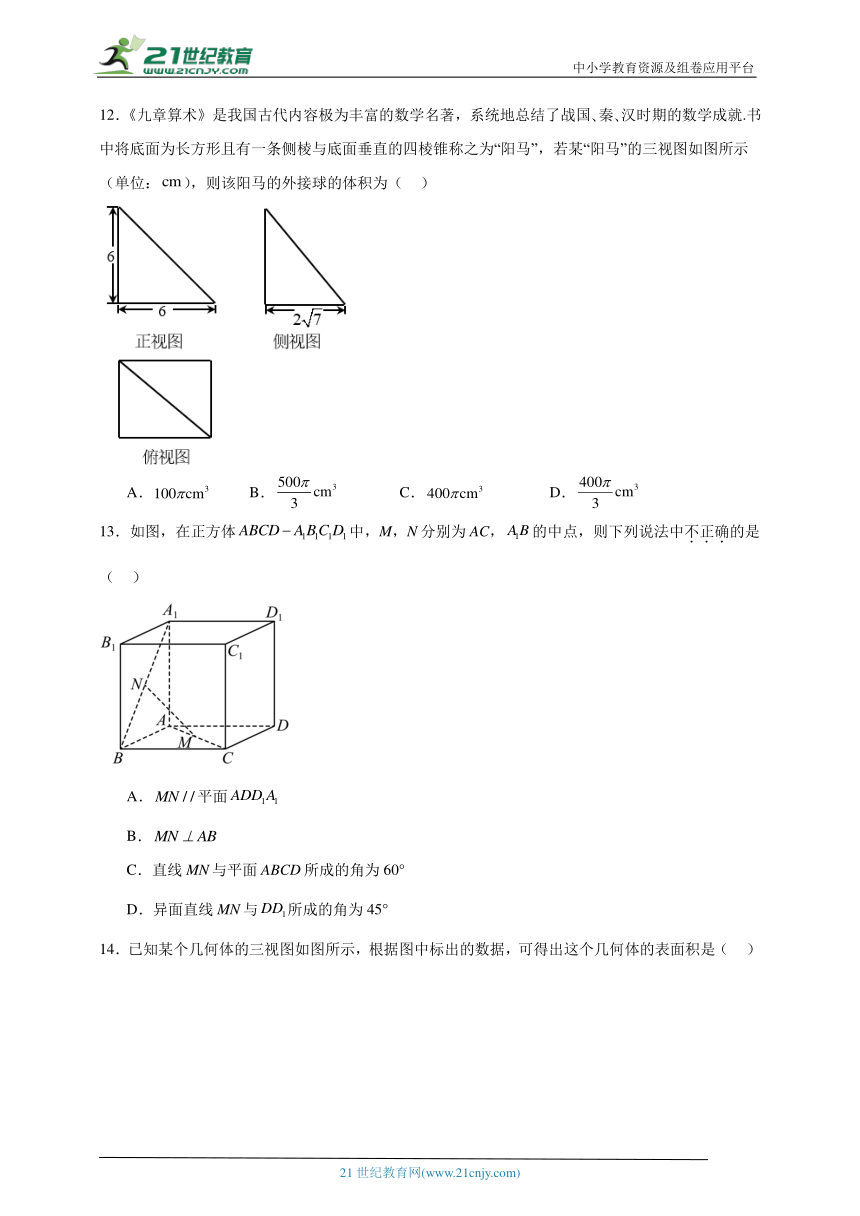
12.《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国 秦 汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:),则该阳马的外接球的体积为( )
A. B. C. D.
13.如图,在正方体中,M,N分别为AC,的中点,则下列说法中不正确的是( )
A.平面
B.
C.直线MN与平面ABCD所成的角为60°
D.异面直线MN与所成的角为45°
14.已知某个几何体的三视图如图所示,根据图中标出的数据,可得出这个几何体的表面积是( )
A.6 B. C. D.
15.三棱锥的所有顶点都在球O的表面上,且,,,则球O的表面积为( )
A.16π B.32π C. D.
16.已知三棱锥的底面ABC是等边三角形,平面SAC⊥平面ABC,,M为SB上一点,且.设三棱锥外接球球心为O,则( )
A.直线OM⊥平面SAC,OA⊥SB B.直线平面SAC,OA⊥SB
C.直线OM⊥平面SAC,平面OAM⊥平面SBC D.直线平面SAC,平面OAM⊥平面SBC
17.在矩形ABCD中,,,点E在CD上,现将沿AE折起,使面面ABC,当E从D运动到C,求点D在面ABC上的射影K的轨迹长度为( )
A. B. C. D.
18.正方体的棱长为1,点在正方体内部及表面上运动,下列结论错误的是( )
A.若点在线段上运动,则
B.若点在线段上运动,则平面
C.若点在内部及边界上运动,则的最大值为3
D.若点满足,则点轨迹的面积为
19.蹴鞠(如图所示),又名蹴球,蹴圆,筑球,踢圆等,蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动,类似于今日的足球.2006年5月20日,蹴鞠作为非物质文化遗产经国务院批准已列入第一批国家非物质文化遗产名录.已知某鞠(球)的表面上有四个点,,,,且球心在上,,,,则该鞠(球)的表面积为( )
A. B. C. D.
20.已知正四棱锥的底面边长为,高为3.以点为球心,为半径的球与过点的球相交,相交圆的面积为,则球的半径为( )
A.或 B.或
C.或 D.或
二、多选题
21.已知空间中两个角α,β,且角α与角β的两边分别平行,若α=30°,则β=( )
A.30° B.60° C.120° D.150°
22.(多选题)我国古代数学名著《九章算术》中记载的“刍甍”(chumeng)是底面为矩形,顶部只有一条棱的五面体.如下图五面体是一个刍甍,其中四边形为矩形,其中,,与都是等边三角形,且二面角与相等,则长度可能为( )
A.1 B.5 C.9 D.13
23.对于两条不同直线,和两个不同平面,,则下列说法中正确的是( ).
A.若,,则
B.若,,,,则
C.若,,则
D.若,,,则
24.如图,四棱锥的底面是正方形,平面ABCD,,是线段的中点,是线段上的动点,则以下结论正确的是( )
A.平面平面
B.直线与平面所成角正切值的最大值为
C.二面角余弦值的最小值为
D.线段上不存在点,使得平面
25.如图,ABCD是边长为5的正方形,半圆面APD⊥平面ABCD.点P为半圆弧上一动点(点P与点A,D不重合).下列说法正确的是( )
A.三棱锥P-ABD的四个面都是直角三角形
B.三棱锥P一ABD体积的最大值为
C.异面直线PA与BC的距离为定值
D.当直线PB与平面ABCD所成角最大时,平面PAB截四棱锥P-ABCD外接球的截面面积为
三、填空题
26.如图,在正方体中,E是的中点.给出下列三个结论:
①;
②;
③线段的长度大于线段的长度.
其中所有正确结论的序号是 .
27.已知的顶点都在半径为的球的球面上,球心到平面的距离为,则球的表面积为 .
28.无穷符号在数学中是一个重要的符号,该符号的引入为微积分和集合论的研究带来了便利,某校在一次数学活动中以无穷符号为创意来源,设计了如图所示的活动标志,该标志由两个半径分别为15和20的实心小球相交而成,球心距,则该标志的体积为 .
附:一个半径为的球被平面截下的一部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的高(记为),球缺的体积公式为.
29.如图,已知矩形ABCD,,,AF⊥平面ABC,且.E为线段DC上一点,沿直线AE将△ADE翻折成,M为的中点,则三棱锥体积的最小值是 .
30.底边和腰长之比为的等腰三角形被称为“黄金三角形”,四个面都为“黄金三角形”的四面体被称为“黄金四面体”.“黄金四面体”的外接球与内切球表面积之比为 .
四、解答题
31.判断如图所示的多面体是不是棱台?
32.如图,在四棱锥中,底面是直角梯形,,,平面,,.
(1)证明:平面PAC;
(2)求点到平面的距离.
33.若E,F是三棱柱 ABC一A1B1C1 侧棱 BB1和 CC1 上的点,且 B1E =CF,三棱柱的体积为m,求四棱锥 A一BEFC 的体积.
34.如图,点是正方形两对角线的交点,平面,平面,,是线段上一点,且.
(1)证明:三棱锥是正三棱锥;
(2)试问在线段(不含端点)上是否存在一点,使得平面.若存在,请指出点的位置;若不存在,请说明理由.
35.已知是内一点,.
(1)若是的外心,求的余弦值;
(2)若是的垂心,是平面外一点,且平面,当四面体外接球体积最小时,求的值.
参考答案:
1.B
【详解】试题分析:设球的半径为,则有,.
故选B.
考点:球心到截面的距离;球的半径之间的关系.
2.D
【解析】设过作互相垂直的两个平面、截该球所得的两个截面圆分别为圆,,半径分别为,,球半径为,由已知求得,再由勾股定理求得线段的长度.
【详解】如图所示:设过作互相垂直的两个平面、截该球所得的两个截面圆分别为圆,,
半径分别为,,球半径为,
球心到,截该球所得两个截面距离平方之和为8,
,则,
.
故选:.
【点睛】本题考查了球的性质,把空间问题转化为平面问题是解题的关键,属于基础题.
3.C
【分析】根据空间几何体的定义,对选项中的命题判断正误即可.
【详解】对于A,有两个面互相平行,其余四个面都是等腰梯形的六面体不一定为棱台,
因为不能保证各侧棱的延长线交与一点,∴A错误;
对于B,用一个平面去截棱锥,棱锥底面和截面之间的部分不一定为棱台,
因为不能保证截面与底面平行,∴B错误;
对于C,由棱锥的定义知由一个底面为多边形,
其余各面为具有公共顶点的三角形围成的几何体是棱锥,∴C正确;
对于D,一个正方形按不同方向平移所得几何体,可能是正方体,也可能是长方体,D错误.
故选:C.
【点睛】本题主要考查了空间几何体的结构特征应用问题,属于基础题.
4.C
【详解】解:把异面直线a,b平移到相交,使交点为P,此时∠APB=80°,过P点作直线c平分∠APB,这时c与a,b所成角为40°,那么外交平分线上有一条,过P点作直线d垂直a和b,这时d与a,b所成角为90°,直线从c向两边转到d时与a,b所成角单调递增,必有经过50°,因为两边,所以有3条.故选C.
5.A
【分析】根据直线与平面的位置关系,结合题意,即可判断和选择.
【详解】因为,且与异面,故,又,,故∥.
故选:A.
6.B
【分析】
由题意可得∥,则异面直线与所成角(或其补角),进而可得出为等边三角形,从而得出所求角的大小为60°.
【详解】
如下图所示,连接,
因为分别为的中点,则∥,
又因为∥,且,
则为平行四边形,可得∥,
所以∥,
可知异面直线与所成角为(或其补角),
又因为,即为等边三角形
所以,即异面直线与所成角的大小为.
故选:B.
7.D
【分析】根据已知条件分别求出球的半径、三棱柱的底面边长和高,从而求出球冠的面积,再根据正弦定理求出外接圆的半径,即可得解.
【详解】设球的半径为,则,得.设正三棱柱的高为,底面边长为,则,(提示:根据正三棱柱和球的结构特征建立方程组)
得,则球被截掉的两个球缺的高均为1,每个球冠的面积为,又外接圆的半径为,(提示:正弦定理的应用)
故所求表面积为.
故选:D
8.D
【分析】在中,连接交于点,推导出;在中,若存在点N在棱上,则三棱锥的体积最小为;在中,过作,交于点,推导出;在中,当时,平面平面.
【详解】在中,连接交于点,则为的重心,连接,由已知得,则,故错;
在中,若存在点N在棱上,则,当与重合时,取最小值,点到平面距离为,,所以此时,故错;
在中,过作,交于点,在棱上存在点P,使得,则,又因为,所以平面,所以,故错;
在中,当时,由题意得,则,所以,又因为平面,所以,又,所以 平面,因为平面,所以平面平面,故正确.
故选:
【点睛】本题主要考查命题的真假,涉及立体几何中线线、线面之间位置关系的判断,以及几何体体积的求解,属于中档题.
9.D
【分析】由线面垂直的判定定理可得平面,设底面的外心为,外接球的球心为,为的中点,可得四边形为平行四边形,所以,在中,由余弦定理及正弦定理可求,故可求外接球的半径,根据球的表面积公式即可求解.
【详解】因为,,平面,
所以平面.
设底面的外心为,外接球的球心为,则平面,所以.
设为的中点,
因为,所以.
因为平面,平面,
所以,所以.
因此四边形为平行四边形,所以.
因为,,
所以,
由正弦定理,得.
所以该外接球的半径满足,
故该外接球的表面积为.
故选:D.
10.A
【分析】设球心为,三棱柱的上底面的内切圆的圆心为,该圆与边切于点,根据球的几何性质可得为直角三角形,然后根据题中数据求出圆半径,进而求得球的半径,最后可求出球的体积.
【详解】如图,设三棱柱为,且,高.
所以底面为斜边是的直角三角形,设该三角形的内切圆为圆,圆与边切于点,
则圆的半径为.
设球心为,则由球的几何知识得为直角三角形,且,
所以,
即球的半径为,
所以球的体积为.
故选A.
【点睛】本题考查与球有关的组合体的问题,解答本题的关键有两个:
(1)构造以球半径、球心到小圆圆心的距离和小圆半径为三边的直角三角形,并在此三角形内求出球的半径,这是解决与球有关的问题时常用的方法.
(2)若直角三角形的两直角边为,斜边为,则该直角三角形内切圆的半径,合理利用中间结论可提高解题的效率.
11.C
【分析】对四个结论逐一分析判断,
对于①,利用翻折前后这个条件不变,易得平面,从而;
对于②,当平面平面时,四面体ABCD的体积最大,易得出体积;
对于③,当平面平面时,BC与平面ABD所成的角最大,即,计算其正弦值可得出结果;
对于④,在翻折的过程中,BD的中点到四面体四个顶点的距离均相等,所以外接球的直径恒为BD,体积恒为定值.
【详解】如图,当时,∵,∴平面,
∵平面,∴,即①正确;
当平面平面时,四面体ABCD的体积最大,最大值为,即②正确;
当平面平面时,BC与平面ABD所成的角最大,为,而,
∴BC与平面ABD所成角一定小于,即③错误;
在翻折的过程中,和始终是直角三角形,斜边都是BD,其外接球的球心永远是BD的中点,外接球的直径为BD,
∴四面体ABCD的外接球的体积不变,即④正确.
故正确的有①②④.
故选:C.
【点睛】本题考查图形翻折的应用,解题关键是应抓住翻折前后的“不变量”和“变量”,进而分析计算,侧重考查直观想象和数学运算的核心素养,属于常考题.
12.B
【分析】由三视图可得几何体为四棱锥,且其中一条侧棱与底面垂直,再由几何体的性质求外接球的半径,进而求其体积.
【详解】由三视图知:几何体是四棱锥,且其中一条侧棱与底面垂直,如下图,平面,
∴,,,
∴该几何体放在长方体中,可得其的外接球的半径为,该阳马的外接球的体积为,
故选:B.
13.C
【分析】取棱中点,利用线面平行的判定推理判断A;利用线面垂直的性质推理判断B;求出线面角、线线角判断CD作答.
【详解】在正方体中,取棱中点,连接,
因为M,N分别为AC,的中点,则,
因此四边形为平行四边形,则平面,
平面,所以平面,A正确;
因为平面,则,所以,B正确;
显然平面,则是与平面所成的角,又,
有,由于,所以直线MN与平面ABCD所成的角为,C错误;
因为,,则是异面直线MN与所成的角,显然,D正确.
故选:C
14.C
【分析】由已知中几何体的三视图,我们可以判断出该几何体是底面是一个底和高均为2的等腰三角形,侧面由一个底和高均为2的等腰三角形和两个腰长为底面长为的等腰三角形,分别求出各面面积,累加可得结果.
【详解】由三视图得几何体原图如图所示,该几何体是一个在俯视图为底面的三棱锥,底面是一个底和高均为2的等腰三角形,高为2,一个侧面由一个底和高均为2的等腰三角形,
另外两个侧面是腰长为,底边长为的等腰三角形,其高为,
故其表面积为.
故选:C.
【点睛】本题考查的知识点是由三视图求面积,其中判断出几何体各面的形状是解答本题的关键.
15.C
【分析】首先证明平面,再利用正弦定理和勾股定理即可求出外接球半径,再利用球的表面积公式即可得到答案.
【详解】,,
,平面,平面,
作出的外接圆圆心,设其外接圆半径为,,
则,
则根据正弦定理有,则,
在图中作出外接球球心,设外接球半径为,
则,平面,因为,则为中点,则,
平面,平面,则,
同理,则四边形为矩形,则,
在中,由勾股定理得,即,
则球O的表面积为.
故选:C.
【点睛】关键点睛:本题的关键是求出的外接圆半径,再作出图形,利用勾股定理即可求出外接球半径的平方,再利用球的表面积公式即可得到答案.
16.D
【分析】画出几何图形,根据题意先找出和的外心,通过两个外心与平面的位置关系确定出球心位置,再根据线面垂直判断OA与SB的位置关系,继而可判断平面OAM与平面SBC的位置关系,最后根据线线平行判断出直线OM与平面SAC的位置关系.
【详解】第1步:判断OA与SB的位置关系,
如图,取AC的中点E,BC的中点F,
连接AF,BE,设AF与BE的交点为O,连接OM,
则O为外心,E为外心,
因为平面SAC⊥平面ABC,
所以O为三棱锥S-ABC外接球球心,
因为SE⊥AC,BE⊥AC,,
所以AC⊥平面SBE,
又平面SBE,所以AC⊥SB,
假设OA⊥SB,因为,所以SB⊥平面ABC,
如图显然SB不垂直于平面ABC,所以OA不垂直于SB,故A、B错误;
第2步:判断平面OAM与平面SBC的位置关系,
因为AM⊥BC,AF⊥BC,,
所以BC⊥平面AMF,
又平面SBC,
所以平面OAM⊥平面SBC;
第3步:判断直线OM与平面SAC的位置关系,
因为AC⊥平面SBE,所以AC⊥OM,
因为BC⊥平面AMF,所以BC⊥OM,
又,所以OM⊥平面ABC,
又SE⊥平面ABC,所以,
所以直线平面SAC,故C错误, D正确.
故选:D.
【点睛】方法点睛:
解几何体外接球(表面积/体积)的一般方法和步骤为:
1、寻找一个或两个面的外接圆圆心
2、分别过两个面的外心作该面的垂线,两条垂线的交点即为外接圆圆心;
3、构造直角三角形求解球半径,进而求出外接球表面积或体积.
17.D
【分析】在原平面矩形中,连接,由面面ABC知,故点的轨迹是以为直径的圆上一段弧,根据的位置求出此弧的长度.
【详解】
由题意,将沿折起,使平面平面,在平面内过点作垂足为在平面上的射影,连接,由翻折的特征知,
则,故点的轨迹是以为直径的圆上一段弧,根据长方形知圆半径是,
如图当与重合时,,所以,
取为的中点,得到是正三角形.
故,
其所对的弧长为;
故选:D.
18.C
【分析】利用线面垂直的性质定理及判定定理可证得A;利用线面平行的判定定理,面面平行的判定定理及性质定理即可证得B;当点与点重合时,最大,可判断C;点的轨迹为半径为1的球的的表面,结合球的表面积公式即可求解D.
【详解】对于A,在正方体中,平面,平面,,又,,平面,平面,又平面,,故A正确;
对于B,在正方体中,,又平面,平面,平面,同理可知平面,又,,平面,所以平面平面,又平面,平面,故B正确;
对于C,在正方体中,当点与点重合时,最大,此时,故C错误;
对于D,点的轨迹为半径为1的球的的表面,所以点的轨迹的面积为半径为1的球的表面积的,所以,故D正确.
故选:C
19.C
【分析】画出图形,作出辅助线,求出,进而得到,利用勾股定理求出球的半径,求出球的表面积.
【详解】如图,取AB的中点M,连接MP,由AC=BC=4,AC⊥BC得:,
由,得:,
连接CM并延长,交球O于点H,连接PH,因为PC球O的直径,
设球的半径为R,则PH⊥CH,,
则,
所以,
解得:,球的表面积为.
故选:C
【点睛】立体几何中外接球问题,要画出具体图形,找到球心的位置,结合解三角形等知识进行求出半径,再求解球的表面积或体积.
20.B
【分析】分公共圆面在四棱锥内部与外部讨论,设相交圆的圆心为,点为相交圆上的一点,球的半径为,可求得相交圆半径为1,由勾股定理得,,组成方程组求解.
【详解】当公共圆面在四棱锥内部时,如下图所示,
设相交圆的圆心为,点为相交圆上的一点,也是两球的公共点,
设球的半径为,
因为相交圆的面积为,所以相交圆的半径为1,即
底面正方形边长为,所以,
由勾股定理有,所以,
设,则①,②,
联立①②解得.
当公共圆面在四棱锥外部时,如下图所示,
同上可求,,,
则③,④,
联立③④解得.
故选:B.
【点睛】方法点睛:在球与截面的计算中方法:球心与圆心之间的距离为,球半径为,截面半径为,可以根据勾股定理建立关系式.
21.AD
【分析】直接由相等或互补求解即可.
【详解】由题意知:或,则或.
故选:AD.
22.BC
【分析】本题分二面角和趋向于、二面角和趋向于两种情况讨论得到的取值范围,再根据范围选择答案即可.
【详解】由于与都是等边三角形,且边长为,故高为.当和趋向于时,,如下图所示.
当和趋向于时,,如下图所示.
所以的取值范围是.
故选:BC.
【点睛】本题考查二面角的定义,是基础题.
23.AD
【解析】根据空间中直线、平面的平行垂直的定义、性质逐项进行判断.
【详解】A.若,,因为垂直于同一平面的两条直线互相平行,所以,故正确;
B.当相交时,;当平行时,不一定成立,故错误;
C.记,当时,,当不垂直于时,此时不成立,故错误;
D.因为,,所以或,又因为,所以,故正确,
故选:AD.
【点睛】易错点睛:本题考查空间中直线、平面的位置关系的判断,属于中档题.判断空间中的线、面平行垂直关系应注意:
(1)判断线面平行时,注意说明线是否在面内;
(2)判断面面平行时,注意说明是相交直线;
(3)判断线面垂直时,注意说明平面外一条直线垂直平面内两条相交直线.
24.ABC
【分析】对于A,利用线面垂直与面面垂直的判定定理证明即可;对于BC,利用线面角与面面角的定义,结合的取值范围求解即可;对于D,找特殊点与重合时,证得平面,由此得解.
【详解】对于A,因为底面,平面,所以.
因为为正方形,所以,
又,平面,平面,所以平面.
因为平面,所以.
因为,为线段的中点,所以,
又因为,平面,平面,所以平面.
又因为平面,所以平面平面,故A正确;
对于B,由选项A可知平面,
所以为直线与平面所成角,则,
不妨设,则在中,,
在中,,
因为是线段上的动点,故,则,
所以直线与平面所成角正切值的最大值为,故B正确;
对于C,由选项A可知平面,平面,
所以,则为二面角的平面角,
因为,
所以二面角余弦值的最小值为,故C正确;
对于D,当与重合时,连接,连接,如图,
因为底面是正方形,所以是的中点,
又为线段的中点,所以,
又平面,平面,所以平面,
即线段上存在点,使得平面,故D错误.
故选:ABC.
【点睛】关键点睛:本题解决的关键是利用线面垂直的判定定理证得平面与平面,从而得到直线与平面所成角与二面角的平面角,由此得解.
25.AC
【分析】利用面面垂直和线面垂直的性质可得,由平面几何知识可证明,,,由此可判断选项A;
当点是半圆弧的中点时,三棱锥的底面积取得最大值,求解即可判断选项B;
证明为异面直线与的距离,即可判断选项C;
过点作于点,连接,确定为直线与平面所成的角,利用平面几何知识,表示出,利用基本不等式求解最值,即可得到答案.由题意可得正方形的中心即为四棱锥的外接球的球心,可得外接球的半径,代入球的表面积公式得答案.
【详解】对于A选项,因为底面为边长是4的正方形,则,
又半圆平面,半圆平面,平面,
则半圆,
又平面,
故,
则为直角三角形,
所以,
因为是圆的直径,
则,
故为直角三角形,
所以,
因为,
则是直角三角形,
所以,
在中,,
则,
所以为直角三角形,
故三棱锥的每个侧面三角形都是直角三角形,
故选项A正确;
对于B选项,在三棱锥中,半圆面,
则是三棱锥的高,
当点是半圆弧的中点时,三棱锥的底面积取得最大值,
三棱锥的体积取得最大值为,
故选项B错误;
因为半圆面平面,,半圆面平面,
所以半圆面,又半圆面,所以,又,
所以为异面直线与的距离,所以异面直线与的距离为定值;故C正确;
对于D选项,取的中点,由选项A中的解析可得,,
所以点为四棱锥外接球的球心,
过点作于点,连接,如图所示,
因为半圆面平面,半圆面平面,
故平面,
所以为在平面内的射影,
则为直线与平面所成的角,
设,则,,
在中,,
,
所以,
故,
令,则,且,
所以,
当且仅当,即时取等号,
所以,
则,
所以直线与平面所成最大角的正弦值为,
则,
所以球心到面的距离满足,
设截面半径为,则有,所以截面面积为,故D错误;
故选:AC.
【点睛】本题以命题的真假判断为载体,考查了空间直线与直线、直线与平面、平面与平面的位置关系,空间几何体外接球的理解与应用,空间角、空间几何体的体积的计算等知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想等,属于难题.
26.①②③
【分析】连接,可判断①;连接、可判断②,通过计算可判断③.
【详解】连接、 、,并设正方体的棱长为.
对于①,由于,可知平面,①正确;
对于②,由于,又是的中点,易知,②正确;
对于③,、、是正方体的面对角线,可知,
因此是等边三角形,而是等边三角形边上的高线,因此,③正确.
故答案为:①②③
27.
【分析】首先利用正余弦定理求出底面外接圆的半径,结合条件和球的截面的性质和,求得,再由球的体积公式计算即可得到所求值.
【详解】解:在底面中,由余弦定理得:
又,则,由正弦定理得:,
所在外接圆的半径,如图,即
球心到平面的距离为,
且,
可得,
则球的表面积是.
故答案为:.
28.
【分析】作出大圆截图,利用弦心距、直角三角形得到两个球缺的高,再利用球的体积公式、球缺的体积公式进行求解.
【详解】记两球面的交线为圆,其大圆截面如图所示,
则,且,
解得,,且圆的半径为12,
两球体的公共部分可看作两个球缺,
小球中的球缺高为,,
大球中的球缺高为,,
故
.
故答案为:.
29.
【分析】首先分析出,即求棱锥体积的最小值即求点到平面的距离的最小值,转化为求点到平面距离的最小值,由条件确定点的运动轨迹为以为球心,半径为1的球面的一部分,然后根据图象分析点到平面距离的最小值.
【详解】因为平面,所以,
又因为,,
所以平面,
所以
,
所以,
所以求棱锥体积的最小值即求点到平面的距离的最小值,
因为点是的中点,
所以点到平面的距离是点到平面距离的一半,
因为,随着点在线段上移动,
点的运动轨迹为以为球心,半径为1的球面的一部分,
因为平面,所以平面平面,并且交于,
所以如图,过点作,即平面,
当为与球面的交点时,到平面的距离最小,
此时点在线段上,
根据,
可得,此时,
即到平面的距离的最小值是,那么点到平面距离的最小值是,
所以三棱锥体积的最小值是.
故答案为:
【点睛】本题考查三棱锥体积的最小值,考查空间点的轨迹问题,意在考查空间想象能力,和数形结合分析问题的能力,属于中档题型.
30.
【分析】画出符合题意的四面体,由其特征将其补形为长方体,分别计算外接球与内切球表面积可得答案.
【详解】如图,设四面体为“黄金四面体”,
且,
得,
又因四个面都为“黄金三角形”,则.
注意到四面体对棱相等,则将其补形为如图所示长方体,则该长方体外接球与该四面体外接球重合.
设,
则长方体外接球半径为长方体体对角线长度的一半,有,又注意到:,
得,又,得.
注意到,
,
则.
又在中,,取中点为E,
则,故,
又由前面分析可知四面体的四个面全等,
则四面体的表面积.
设四面体的内切球半径为,则,
得.
注意到,则,
又,得,又,
则.
则“黄金四面体”的外接球与内切球表面积之比为:
,
代入,得比值为:.
故答案为:
【点睛】关键点点睛:本题涉及求几何体的外接球半径及内切球半径,难度较大.题目关键为由题目条件得到“黄金四面体”的对棱相等,从而将其补形为长方体,而适当的代换也可减小计算的复杂度.
31.图(1)不是棱台;图(2)不是棱台;图(3)不是棱台.
【解析】根据棱台的定义判断.
【详解】判断棱台的标准:一是共点,即各侧棱延长线要交于一点;二是平行,即上、下两个底面要平行.据此可知,图(1)中多面体的侧被延长线不相交于一点,故不是棱台;图(2)中多面体不是由棱锥截得的,侧棱延长线不相交于一点,故不是棱台;图(3)中多面体截面与底面不平行,故不是棱台.
【点睛】本题考查棱台的概念,掌握棱台定义是解题关键.
32.(1)证明见解析;
(2).
【分析】(1)证明,即可由线线垂直证明线面垂直;
(2)利用等体积法,结合棱锥体积的计算公式,即可求得结果.
【详解】(1)底面为直角梯形,,,故可得,
又,则,易知,
故,则;
又面面,故;
又面,故面.
(2)由(1)知面,又面,故,
又面面,故,则,
又,则;
因为面,故点到面的距离为,也即点到面的距离为;
又,
设点到面的距离为,则由可得:
,则,解得,
故点到面的距离为.
33.
【分析】根据以及棱锥体积和棱柱体积之间的关系即可得解.
【详解】如图所示,
连接 AB1,AC1.因为 B1E =CF,
所以 梯形 BEFC 的面积等于梯形 B1EFC1的面积.
又四棱锥 A -BEFC 的高与四棱锥 A- B1EFC1的高相等,
所以=,设棱柱ABC一A1B1C1的高为h
又,所以,
所以
即四棱锥 A BEFC 的体积是.
34.(1)证明见解析;(2)不存在,理由见解析.
【分析】(1)根据正三棱锥的定义即可证明;
(2)利用反证法,由平面,假设存在这样的点,使得平面,推出平面平面,与平面和平面是相交平面矛盾,即可求解.
【详解】解:(1)证明:设,
则
∴是正三角形,
如图所示:连接,,
,
∴,,,
在中,由知:.
又平面,
,
∵,,
∴平面,
∴.
又平面,,
∴平面,
在线段上取点,使得,
则点是的重心,也就是的中心,
连接,则,
∴平面,
∴三棱锥是正三棱锥;
(2)∵平面与平面有公共点,
故平面与平面是相交平面,
∵,平面,平面,
∴平面,
假设存在这样的点,使得平面,
∵点与点不重合,
∴与是相交直线,
又平面,平面,且平面,平面,
∴平面平面,
这与平面和平面是相交平面矛盾,
∴不存在一点,使得平面.
35.(1)
(2)
【分析】(1)取中点,中点,分别连接,再根据,由向量垂直的数量积解出三边长度关系即可.
(2)取中点,在上取,在上取,分别连接,延长交于点,先根据解出三边长度关系,再证明出四边形是长方形得到的长度,最后在四面体中找到外接球球心的位置,且当外接球球心刚好与的外心重合时,外接球半径最小,体积也最小.
【详解】(1)取中点,中点,
分别连接,如图:
是的外心,是三条边上垂直平分线的交点,
,
则,
,
设,,,
则,
由余弦定理可得,
即,
令,解得,,
则.
故的余弦值为.
(2)取各边中点,连接成,如图:
则,且相似比为.
设是的外心,则,
由中位线平行底边可得,,
即是的垂心,由相似可得,即.
在上取,在上取,
分别连接,延长交于点,如图:
是的垂心,
,
又,
四边形是平行四边形.
则,
,
设,,,
则,
由余弦定理可得,
即,
令,解得,,
则,,
由正弦定理可得的外接圆半径,
.
,
又
,即,
所以,四边形是平行四边形,且为长方形,
在中,,
则.
在四面体中,设平面,且,
分别连接,如图:
由平面,可得,
设,
则,
,
当时,是四面体的外接球球心,是四面体的外接球半径,
解可得,
当四面体的外接球体积最小时,半径也最小,
而半径取最小值时,,
此时,解得,
则.
故当四面体外接球体积最小时,的值为.
【点睛】方法点睛:对于存在外接球的棱锥,求外接球球心位置的通用方法,即先找底面外接圆圆心,再过圆心作底面的垂线,则外接球球心一定在这条垂线上,再通过外接球球心到顶点的距离等于到底边图形顶点的距离,即可确定外接球球心的位置.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
必修二难点 立体几何初步1
一、单选题
1.一平面截球O得到半径为cm的圆面,球心到这个平面的距离是2cm,则球O的体积是
A.12π cm3 B.36π cm3 C.cm3 D.cm3
2.已知A,B是半径为的球面上的两点,过AB作互相垂直的两个平面,若球心到截该球所得两个截面距离平方之和为8,则线段AB的长度是
A. B.2 C. D.4
3.下列命题正确的是( )
A.有两个面互相平行,其余四个面都是等腰梯形的六面体为棱台
B.用一个平面去截棱锥,棱锥底面和截面之间的部分为棱台
C.棱锥是由一个底面为多边形,其余各面为具有公共顶点的三角形围成的几何体
D.一个正方形按不同方向平移所得几何体都是正方体
4.已知异面直线A.与b成80的角,p为空间一定点,则过点p与A.,b所成的角都是50的直线有且仅有( ).
A.1条 B.2条 C.3条 D.4条
5.已知为两两垂直的三条异面直线,过作平面α与直线垂直,则直线与平面的关系是( )
A.∥ B.∥或
C.或与不平行 D.
6.在正方体中,分别为的中点,则异面直线与所成角的大小为( )
A. B. C. D.
7.球缺是指一个球被平面截下的部分,截面为球缺的底面,垂直于截面的直径被截面截得的线段长为球缺的高,球缺曲面部分的面积(球冠面积)(为球的半径,为球缺的高).已知正三棱柱的顶点都在球的表面上,球的表面积为,该正三棱柱的体积为,若的边长为整数,则球被该正三棱柱上、下底面所在平面截掉两个球缺后剩余部分的表面积为( )
A. B. C. D.
8.如图,在三棱柱中,底面分别是棱的中点,点F在棱上,,则下列说法正确的是( )
A.设平面与平面的交线为l,则直线与l相交
B.在棱上存在点N,使得三棱锥的体积为
C.在棱上存在点P,使得
D.设点M在上,当时,平面平面
9.在四面体中,,,,,则该四面体的外接球的表面积为( )
A. B. C. D.
10.如图所示,直三棱柱的高为4,底面边长分别是5,12,13,当球与上底面三条棱都相切时球心到下底面距离为8,则球的体积为
A. B. C. D.
11.在矩形ABCD中,,,沿矩形对角线BD将折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当时,;②四面体ABCD的体积的最大值为;③在四面体ABCD中,BC与平面ABD所成角可能为;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为
A.①④ B.①② C.①②④ D.②③④
12.《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国 秦 汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:),则该阳马的外接球的体积为( )
A. B. C. D.
13.如图,在正方体中,M,N分别为AC,的中点,则下列说法中不正确的是( )
A.平面
B.
C.直线MN与平面ABCD所成的角为60°
D.异面直线MN与所成的角为45°
14.已知某个几何体的三视图如图所示,根据图中标出的数据,可得出这个几何体的表面积是( )
A.6 B. C. D.
15.三棱锥的所有顶点都在球O的表面上,且,,,则球O的表面积为( )
A.16π B.32π C. D.
16.已知三棱锥的底面ABC是等边三角形,平面SAC⊥平面ABC,,M为SB上一点,且.设三棱锥外接球球心为O,则( )
A.直线OM⊥平面SAC,OA⊥SB B.直线平面SAC,OA⊥SB
C.直线OM⊥平面SAC,平面OAM⊥平面SBC D.直线平面SAC,平面OAM⊥平面SBC
17.在矩形ABCD中,,,点E在CD上,现将沿AE折起,使面面ABC,当E从D运动到C,求点D在面ABC上的射影K的轨迹长度为( )
A. B. C. D.
18.正方体的棱长为1,点在正方体内部及表面上运动,下列结论错误的是( )
A.若点在线段上运动,则
B.若点在线段上运动,则平面
C.若点在内部及边界上运动,则的最大值为3
D.若点满足,则点轨迹的面积为
19.蹴鞠(如图所示),又名蹴球,蹴圆,筑球,踢圆等,蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动,类似于今日的足球.2006年5月20日,蹴鞠作为非物质文化遗产经国务院批准已列入第一批国家非物质文化遗产名录.已知某鞠(球)的表面上有四个点,,,,且球心在上,,,,则该鞠(球)的表面积为( )
A. B. C. D.
20.已知正四棱锥的底面边长为,高为3.以点为球心,为半径的球与过点的球相交,相交圆的面积为,则球的半径为( )
A.或 B.或
C.或 D.或
二、多选题
21.已知空间中两个角α,β,且角α与角β的两边分别平行,若α=30°,则β=( )
A.30° B.60° C.120° D.150°
22.(多选题)我国古代数学名著《九章算术》中记载的“刍甍”(chumeng)是底面为矩形,顶部只有一条棱的五面体.如下图五面体是一个刍甍,其中四边形为矩形,其中,,与都是等边三角形,且二面角与相等,则长度可能为( )
A.1 B.5 C.9 D.13
23.对于两条不同直线,和两个不同平面,,则下列说法中正确的是( ).
A.若,,则
B.若,,,,则
C.若,,则
D.若,,,则
24.如图,四棱锥的底面是正方形,平面ABCD,,是线段的中点,是线段上的动点,则以下结论正确的是( )
A.平面平面
B.直线与平面所成角正切值的最大值为
C.二面角余弦值的最小值为
D.线段上不存在点,使得平面
25.如图,ABCD是边长为5的正方形,半圆面APD⊥平面ABCD.点P为半圆弧上一动点(点P与点A,D不重合).下列说法正确的是( )
A.三棱锥P-ABD的四个面都是直角三角形
B.三棱锥P一ABD体积的最大值为
C.异面直线PA与BC的距离为定值
D.当直线PB与平面ABCD所成角最大时,平面PAB截四棱锥P-ABCD外接球的截面面积为
三、填空题
26.如图,在正方体中,E是的中点.给出下列三个结论:
①;
②;
③线段的长度大于线段的长度.
其中所有正确结论的序号是 .
27.已知的顶点都在半径为的球的球面上,球心到平面的距离为,则球的表面积为 .
28.无穷符号在数学中是一个重要的符号,该符号的引入为微积分和集合论的研究带来了便利,某校在一次数学活动中以无穷符号为创意来源,设计了如图所示的活动标志,该标志由两个半径分别为15和20的实心小球相交而成,球心距,则该标志的体积为 .
附:一个半径为的球被平面截下的一部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的高(记为),球缺的体积公式为.
29.如图,已知矩形ABCD,,,AF⊥平面ABC,且.E为线段DC上一点,沿直线AE将△ADE翻折成,M为的中点,则三棱锥体积的最小值是 .
30.底边和腰长之比为的等腰三角形被称为“黄金三角形”,四个面都为“黄金三角形”的四面体被称为“黄金四面体”.“黄金四面体”的外接球与内切球表面积之比为 .
四、解答题
31.判断如图所示的多面体是不是棱台?
32.如图,在四棱锥中,底面是直角梯形,,,平面,,.
(1)证明:平面PAC;
(2)求点到平面的距离.
33.若E,F是三棱柱 ABC一A1B1C1 侧棱 BB1和 CC1 上的点,且 B1E =CF,三棱柱的体积为m,求四棱锥 A一BEFC 的体积.
34.如图,点是正方形两对角线的交点,平面,平面,,是线段上一点,且.
(1)证明:三棱锥是正三棱锥;
(2)试问在线段(不含端点)上是否存在一点,使得平面.若存在,请指出点的位置;若不存在,请说明理由.
35.已知是内一点,.
(1)若是的外心,求的余弦值;
(2)若是的垂心,是平面外一点,且平面,当四面体外接球体积最小时,求的值.
参考答案:
1.B
【详解】试题分析:设球的半径为,则有,.
故选B.
考点:球心到截面的距离;球的半径之间的关系.
2.D
【解析】设过作互相垂直的两个平面、截该球所得的两个截面圆分别为圆,,半径分别为,,球半径为,由已知求得,再由勾股定理求得线段的长度.
【详解】如图所示:设过作互相垂直的两个平面、截该球所得的两个截面圆分别为圆,,
半径分别为,,球半径为,
球心到,截该球所得两个截面距离平方之和为8,
,则,
.
故选:.
【点睛】本题考查了球的性质,把空间问题转化为平面问题是解题的关键,属于基础题.
3.C
【分析】根据空间几何体的定义,对选项中的命题判断正误即可.
【详解】对于A,有两个面互相平行,其余四个面都是等腰梯形的六面体不一定为棱台,
因为不能保证各侧棱的延长线交与一点,∴A错误;
对于B,用一个平面去截棱锥,棱锥底面和截面之间的部分不一定为棱台,
因为不能保证截面与底面平行,∴B错误;
对于C,由棱锥的定义知由一个底面为多边形,
其余各面为具有公共顶点的三角形围成的几何体是棱锥,∴C正确;
对于D,一个正方形按不同方向平移所得几何体,可能是正方体,也可能是长方体,D错误.
故选:C.
【点睛】本题主要考查了空间几何体的结构特征应用问题,属于基础题.
4.C
【详解】解:把异面直线a,b平移到相交,使交点为P,此时∠APB=80°,过P点作直线c平分∠APB,这时c与a,b所成角为40°,那么外交平分线上有一条,过P点作直线d垂直a和b,这时d与a,b所成角为90°,直线从c向两边转到d时与a,b所成角单调递增,必有经过50°,因为两边,所以有3条.故选C.
5.A
【分析】根据直线与平面的位置关系,结合题意,即可判断和选择.
【详解】因为,且与异面,故,又,,故∥.
故选:A.
6.B
【分析】
由题意可得∥,则异面直线与所成角(或其补角),进而可得出为等边三角形,从而得出所求角的大小为60°.
【详解】
如下图所示,连接,
因为分别为的中点,则∥,
又因为∥,且,
则为平行四边形,可得∥,
所以∥,
可知异面直线与所成角为(或其补角),
又因为,即为等边三角形
所以,即异面直线与所成角的大小为.
故选:B.
7.D
【分析】根据已知条件分别求出球的半径、三棱柱的底面边长和高,从而求出球冠的面积,再根据正弦定理求出外接圆的半径,即可得解.
【详解】设球的半径为,则,得.设正三棱柱的高为,底面边长为,则,(提示:根据正三棱柱和球的结构特征建立方程组)
得,则球被截掉的两个球缺的高均为1,每个球冠的面积为,又外接圆的半径为,(提示:正弦定理的应用)
故所求表面积为.
故选:D
8.D
【分析】在中,连接交于点,推导出;在中,若存在点N在棱上,则三棱锥的体积最小为;在中,过作,交于点,推导出;在中,当时,平面平面.
【详解】在中,连接交于点,则为的重心,连接,由已知得,则,故错;
在中,若存在点N在棱上,则,当与重合时,取最小值,点到平面距离为,,所以此时,故错;
在中,过作,交于点,在棱上存在点P,使得,则,又因为,所以平面,所以,故错;
在中,当时,由题意得,则,所以,又因为平面,所以,又,所以 平面,因为平面,所以平面平面,故正确.
故选:
【点睛】本题主要考查命题的真假,涉及立体几何中线线、线面之间位置关系的判断,以及几何体体积的求解,属于中档题.
9.D
【分析】由线面垂直的判定定理可得平面,设底面的外心为,外接球的球心为,为的中点,可得四边形为平行四边形,所以,在中,由余弦定理及正弦定理可求,故可求外接球的半径,根据球的表面积公式即可求解.
【详解】因为,,平面,
所以平面.
设底面的外心为,外接球的球心为,则平面,所以.
设为的中点,
因为,所以.
因为平面,平面,
所以,所以.
因此四边形为平行四边形,所以.
因为,,
所以,
由正弦定理,得.
所以该外接球的半径满足,
故该外接球的表面积为.
故选:D.
10.A
【分析】设球心为,三棱柱的上底面的内切圆的圆心为,该圆与边切于点,根据球的几何性质可得为直角三角形,然后根据题中数据求出圆半径,进而求得球的半径,最后可求出球的体积.
【详解】如图,设三棱柱为,且,高.
所以底面为斜边是的直角三角形,设该三角形的内切圆为圆,圆与边切于点,
则圆的半径为.
设球心为,则由球的几何知识得为直角三角形,且,
所以,
即球的半径为,
所以球的体积为.
故选A.
【点睛】本题考查与球有关的组合体的问题,解答本题的关键有两个:
(1)构造以球半径、球心到小圆圆心的距离和小圆半径为三边的直角三角形,并在此三角形内求出球的半径,这是解决与球有关的问题时常用的方法.
(2)若直角三角形的两直角边为,斜边为,则该直角三角形内切圆的半径,合理利用中间结论可提高解题的效率.
11.C
【分析】对四个结论逐一分析判断,
对于①,利用翻折前后这个条件不变,易得平面,从而;
对于②,当平面平面时,四面体ABCD的体积最大,易得出体积;
对于③,当平面平面时,BC与平面ABD所成的角最大,即,计算其正弦值可得出结果;
对于④,在翻折的过程中,BD的中点到四面体四个顶点的距离均相等,所以外接球的直径恒为BD,体积恒为定值.
【详解】如图,当时,∵,∴平面,
∵平面,∴,即①正确;
当平面平面时,四面体ABCD的体积最大,最大值为,即②正确;
当平面平面时,BC与平面ABD所成的角最大,为,而,
∴BC与平面ABD所成角一定小于,即③错误;
在翻折的过程中,和始终是直角三角形,斜边都是BD,其外接球的球心永远是BD的中点,外接球的直径为BD,
∴四面体ABCD的外接球的体积不变,即④正确.
故正确的有①②④.
故选:C.
【点睛】本题考查图形翻折的应用,解题关键是应抓住翻折前后的“不变量”和“变量”,进而分析计算,侧重考查直观想象和数学运算的核心素养,属于常考题.
12.B
【分析】由三视图可得几何体为四棱锥,且其中一条侧棱与底面垂直,再由几何体的性质求外接球的半径,进而求其体积.
【详解】由三视图知:几何体是四棱锥,且其中一条侧棱与底面垂直,如下图,平面,
∴,,,
∴该几何体放在长方体中,可得其的外接球的半径为,该阳马的外接球的体积为,
故选:B.
13.C
【分析】取棱中点,利用线面平行的判定推理判断A;利用线面垂直的性质推理判断B;求出线面角、线线角判断CD作答.
【详解】在正方体中,取棱中点,连接,
因为M,N分别为AC,的中点,则,
因此四边形为平行四边形,则平面,
平面,所以平面,A正确;
因为平面,则,所以,B正确;
显然平面,则是与平面所成的角,又,
有,由于,所以直线MN与平面ABCD所成的角为,C错误;
因为,,则是异面直线MN与所成的角,显然,D正确.
故选:C
14.C
【分析】由已知中几何体的三视图,我们可以判断出该几何体是底面是一个底和高均为2的等腰三角形,侧面由一个底和高均为2的等腰三角形和两个腰长为底面长为的等腰三角形,分别求出各面面积,累加可得结果.
【详解】由三视图得几何体原图如图所示,该几何体是一个在俯视图为底面的三棱锥,底面是一个底和高均为2的等腰三角形,高为2,一个侧面由一个底和高均为2的等腰三角形,
另外两个侧面是腰长为,底边长为的等腰三角形,其高为,
故其表面积为.
故选:C.
【点睛】本题考查的知识点是由三视图求面积,其中判断出几何体各面的形状是解答本题的关键.
15.C
【分析】首先证明平面,再利用正弦定理和勾股定理即可求出外接球半径,再利用球的表面积公式即可得到答案.
【详解】,,
,平面,平面,
作出的外接圆圆心,设其外接圆半径为,,
则,
则根据正弦定理有,则,
在图中作出外接球球心,设外接球半径为,
则,平面,因为,则为中点,则,
平面,平面,则,
同理,则四边形为矩形,则,
在中,由勾股定理得,即,
则球O的表面积为.
故选:C.
【点睛】关键点睛:本题的关键是求出的外接圆半径,再作出图形,利用勾股定理即可求出外接球半径的平方,再利用球的表面积公式即可得到答案.
16.D
【分析】画出几何图形,根据题意先找出和的外心,通过两个外心与平面的位置关系确定出球心位置,再根据线面垂直判断OA与SB的位置关系,继而可判断平面OAM与平面SBC的位置关系,最后根据线线平行判断出直线OM与平面SAC的位置关系.
【详解】第1步:判断OA与SB的位置关系,
如图,取AC的中点E,BC的中点F,
连接AF,BE,设AF与BE的交点为O,连接OM,
则O为外心,E为外心,
因为平面SAC⊥平面ABC,
所以O为三棱锥S-ABC外接球球心,
因为SE⊥AC,BE⊥AC,,
所以AC⊥平面SBE,
又平面SBE,所以AC⊥SB,
假设OA⊥SB,因为,所以SB⊥平面ABC,
如图显然SB不垂直于平面ABC,所以OA不垂直于SB,故A、B错误;
第2步:判断平面OAM与平面SBC的位置关系,
因为AM⊥BC,AF⊥BC,,
所以BC⊥平面AMF,
又平面SBC,
所以平面OAM⊥平面SBC;
第3步:判断直线OM与平面SAC的位置关系,
因为AC⊥平面SBE,所以AC⊥OM,
因为BC⊥平面AMF,所以BC⊥OM,
又,所以OM⊥平面ABC,
又SE⊥平面ABC,所以,
所以直线平面SAC,故C错误, D正确.
故选:D.
【点睛】方法点睛:
解几何体外接球(表面积/体积)的一般方法和步骤为:
1、寻找一个或两个面的外接圆圆心
2、分别过两个面的外心作该面的垂线,两条垂线的交点即为外接圆圆心;
3、构造直角三角形求解球半径,进而求出外接球表面积或体积.
17.D
【分析】在原平面矩形中,连接,由面面ABC知,故点的轨迹是以为直径的圆上一段弧,根据的位置求出此弧的长度.
【详解】
由题意,将沿折起,使平面平面,在平面内过点作垂足为在平面上的射影,连接,由翻折的特征知,
则,故点的轨迹是以为直径的圆上一段弧,根据长方形知圆半径是,
如图当与重合时,,所以,
取为的中点,得到是正三角形.
故,
其所对的弧长为;
故选:D.
18.C
【分析】利用线面垂直的性质定理及判定定理可证得A;利用线面平行的判定定理,面面平行的判定定理及性质定理即可证得B;当点与点重合时,最大,可判断C;点的轨迹为半径为1的球的的表面,结合球的表面积公式即可求解D.
【详解】对于A,在正方体中,平面,平面,,又,,平面,平面,又平面,,故A正确;
对于B,在正方体中,,又平面,平面,平面,同理可知平面,又,,平面,所以平面平面,又平面,平面,故B正确;
对于C,在正方体中,当点与点重合时,最大,此时,故C错误;
对于D,点的轨迹为半径为1的球的的表面,所以点的轨迹的面积为半径为1的球的表面积的,所以,故D正确.
故选:C
19.C
【分析】画出图形,作出辅助线,求出,进而得到,利用勾股定理求出球的半径,求出球的表面积.
【详解】如图,取AB的中点M,连接MP,由AC=BC=4,AC⊥BC得:,
由,得:,
连接CM并延长,交球O于点H,连接PH,因为PC球O的直径,
设球的半径为R,则PH⊥CH,,
则,
所以,
解得:,球的表面积为.
故选:C
【点睛】立体几何中外接球问题,要画出具体图形,找到球心的位置,结合解三角形等知识进行求出半径,再求解球的表面积或体积.
20.B
【分析】分公共圆面在四棱锥内部与外部讨论,设相交圆的圆心为,点为相交圆上的一点,球的半径为,可求得相交圆半径为1,由勾股定理得,,组成方程组求解.
【详解】当公共圆面在四棱锥内部时,如下图所示,
设相交圆的圆心为,点为相交圆上的一点,也是两球的公共点,
设球的半径为,
因为相交圆的面积为,所以相交圆的半径为1,即
底面正方形边长为,所以,
由勾股定理有,所以,
设,则①,②,
联立①②解得.
当公共圆面在四棱锥外部时,如下图所示,
同上可求,,,
则③,④,
联立③④解得.
故选:B.
【点睛】方法点睛:在球与截面的计算中方法:球心与圆心之间的距离为,球半径为,截面半径为,可以根据勾股定理建立关系式.
21.AD
【分析】直接由相等或互补求解即可.
【详解】由题意知:或,则或.
故选:AD.
22.BC
【分析】本题分二面角和趋向于、二面角和趋向于两种情况讨论得到的取值范围,再根据范围选择答案即可.
【详解】由于与都是等边三角形,且边长为,故高为.当和趋向于时,,如下图所示.
当和趋向于时,,如下图所示.
所以的取值范围是.
故选:BC.
【点睛】本题考查二面角的定义,是基础题.
23.AD
【解析】根据空间中直线、平面的平行垂直的定义、性质逐项进行判断.
【详解】A.若,,因为垂直于同一平面的两条直线互相平行,所以,故正确;
B.当相交时,;当平行时,不一定成立,故错误;
C.记,当时,,当不垂直于时,此时不成立,故错误;
D.因为,,所以或,又因为,所以,故正确,
故选:AD.
【点睛】易错点睛:本题考查空间中直线、平面的位置关系的判断,属于中档题.判断空间中的线、面平行垂直关系应注意:
(1)判断线面平行时,注意说明线是否在面内;
(2)判断面面平行时,注意说明是相交直线;
(3)判断线面垂直时,注意说明平面外一条直线垂直平面内两条相交直线.
24.ABC
【分析】对于A,利用线面垂直与面面垂直的判定定理证明即可;对于BC,利用线面角与面面角的定义,结合的取值范围求解即可;对于D,找特殊点与重合时,证得平面,由此得解.
【详解】对于A,因为底面,平面,所以.
因为为正方形,所以,
又,平面,平面,所以平面.
因为平面,所以.
因为,为线段的中点,所以,
又因为,平面,平面,所以平面.
又因为平面,所以平面平面,故A正确;
对于B,由选项A可知平面,
所以为直线与平面所成角,则,
不妨设,则在中,,
在中,,
因为是线段上的动点,故,则,
所以直线与平面所成角正切值的最大值为,故B正确;
对于C,由选项A可知平面,平面,
所以,则为二面角的平面角,
因为,
所以二面角余弦值的最小值为,故C正确;
对于D,当与重合时,连接,连接,如图,
因为底面是正方形,所以是的中点,
又为线段的中点,所以,
又平面,平面,所以平面,
即线段上存在点,使得平面,故D错误.
故选:ABC.
【点睛】关键点睛:本题解决的关键是利用线面垂直的判定定理证得平面与平面,从而得到直线与平面所成角与二面角的平面角,由此得解.
25.AC
【分析】利用面面垂直和线面垂直的性质可得,由平面几何知识可证明,,,由此可判断选项A;
当点是半圆弧的中点时,三棱锥的底面积取得最大值,求解即可判断选项B;
证明为异面直线与的距离,即可判断选项C;
过点作于点,连接,确定为直线与平面所成的角,利用平面几何知识,表示出,利用基本不等式求解最值,即可得到答案.由题意可得正方形的中心即为四棱锥的外接球的球心,可得外接球的半径,代入球的表面积公式得答案.
【详解】对于A选项,因为底面为边长是4的正方形,则,
又半圆平面,半圆平面,平面,
则半圆,
又平面,
故,
则为直角三角形,
所以,
因为是圆的直径,
则,
故为直角三角形,
所以,
因为,
则是直角三角形,
所以,
在中,,
则,
所以为直角三角形,
故三棱锥的每个侧面三角形都是直角三角形,
故选项A正确;
对于B选项,在三棱锥中,半圆面,
则是三棱锥的高,
当点是半圆弧的中点时,三棱锥的底面积取得最大值,
三棱锥的体积取得最大值为,
故选项B错误;
因为半圆面平面,,半圆面平面,
所以半圆面,又半圆面,所以,又,
所以为异面直线与的距离,所以异面直线与的距离为定值;故C正确;
对于D选项,取的中点,由选项A中的解析可得,,
所以点为四棱锥外接球的球心,
过点作于点,连接,如图所示,
因为半圆面平面,半圆面平面,
故平面,
所以为在平面内的射影,
则为直线与平面所成的角,
设,则,,
在中,,
,
所以,
故,
令,则,且,
所以,
当且仅当,即时取等号,
所以,
则,
所以直线与平面所成最大角的正弦值为,
则,
所以球心到面的距离满足,
设截面半径为,则有,所以截面面积为,故D错误;
故选:AC.
【点睛】本题以命题的真假判断为载体,考查了空间直线与直线、直线与平面、平面与平面的位置关系,空间几何体外接球的理解与应用,空间角、空间几何体的体积的计算等知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想等,属于难题.
26.①②③
【分析】连接,可判断①;连接、可判断②,通过计算可判断③.
【详解】连接、 、,并设正方体的棱长为.
对于①,由于,可知平面,①正确;
对于②,由于,又是的中点,易知,②正确;
对于③,、、是正方体的面对角线,可知,
因此是等边三角形,而是等边三角形边上的高线,因此,③正确.
故答案为:①②③
27.
【分析】首先利用正余弦定理求出底面外接圆的半径,结合条件和球的截面的性质和,求得,再由球的体积公式计算即可得到所求值.
【详解】解:在底面中,由余弦定理得:
又,则,由正弦定理得:,
所在外接圆的半径,如图,即
球心到平面的距离为,
且,
可得,
则球的表面积是.
故答案为:.
28.
【分析】作出大圆截图,利用弦心距、直角三角形得到两个球缺的高,再利用球的体积公式、球缺的体积公式进行求解.
【详解】记两球面的交线为圆,其大圆截面如图所示,
则,且,
解得,,且圆的半径为12,
两球体的公共部分可看作两个球缺,
小球中的球缺高为,,
大球中的球缺高为,,
故
.
故答案为:.
29.
【分析】首先分析出,即求棱锥体积的最小值即求点到平面的距离的最小值,转化为求点到平面距离的最小值,由条件确定点的运动轨迹为以为球心,半径为1的球面的一部分,然后根据图象分析点到平面距离的最小值.
【详解】因为平面,所以,
又因为,,
所以平面,
所以
,
所以,
所以求棱锥体积的最小值即求点到平面的距离的最小值,
因为点是的中点,
所以点到平面的距离是点到平面距离的一半,
因为,随着点在线段上移动,
点的运动轨迹为以为球心,半径为1的球面的一部分,
因为平面,所以平面平面,并且交于,
所以如图,过点作,即平面,
当为与球面的交点时,到平面的距离最小,
此时点在线段上,
根据,
可得,此时,
即到平面的距离的最小值是,那么点到平面距离的最小值是,
所以三棱锥体积的最小值是.
故答案为:
【点睛】本题考查三棱锥体积的最小值,考查空间点的轨迹问题,意在考查空间想象能力,和数形结合分析问题的能力,属于中档题型.
30.
【分析】画出符合题意的四面体,由其特征将其补形为长方体,分别计算外接球与内切球表面积可得答案.
【详解】如图,设四面体为“黄金四面体”,
且,
得,
又因四个面都为“黄金三角形”,则.
注意到四面体对棱相等,则将其补形为如图所示长方体,则该长方体外接球与该四面体外接球重合.
设,
则长方体外接球半径为长方体体对角线长度的一半,有,又注意到:,
得,又,得.
注意到,
,
则.
又在中,,取中点为E,
则,故,
又由前面分析可知四面体的四个面全等,
则四面体的表面积.
设四面体的内切球半径为,则,
得.
注意到,则,
又,得,又,
则.
则“黄金四面体”的外接球与内切球表面积之比为:
,
代入,得比值为:.
故答案为:
【点睛】关键点点睛:本题涉及求几何体的外接球半径及内切球半径,难度较大.题目关键为由题目条件得到“黄金四面体”的对棱相等,从而将其补形为长方体,而适当的代换也可减小计算的复杂度.
31.图(1)不是棱台;图(2)不是棱台;图(3)不是棱台.
【解析】根据棱台的定义判断.
【详解】判断棱台的标准:一是共点,即各侧棱延长线要交于一点;二是平行,即上、下两个底面要平行.据此可知,图(1)中多面体的侧被延长线不相交于一点,故不是棱台;图(2)中多面体不是由棱锥截得的,侧棱延长线不相交于一点,故不是棱台;图(3)中多面体截面与底面不平行,故不是棱台.
【点睛】本题考查棱台的概念,掌握棱台定义是解题关键.
32.(1)证明见解析;
(2).
【分析】(1)证明,即可由线线垂直证明线面垂直;
(2)利用等体积法,结合棱锥体积的计算公式,即可求得结果.
【详解】(1)底面为直角梯形,,,故可得,
又,则,易知,
故,则;
又面面,故;
又面,故面.
(2)由(1)知面,又面,故,
又面面,故,则,
又,则;
因为面,故点到面的距离为,也即点到面的距离为;
又,
设点到面的距离为,则由可得:
,则,解得,
故点到面的距离为.
33.
【分析】根据以及棱锥体积和棱柱体积之间的关系即可得解.
【详解】如图所示,
连接 AB1,AC1.因为 B1E =CF,
所以 梯形 BEFC 的面积等于梯形 B1EFC1的面积.
又四棱锥 A -BEFC 的高与四棱锥 A- B1EFC1的高相等,
所以=,设棱柱ABC一A1B1C1的高为h
又,所以,
所以
即四棱锥 A BEFC 的体积是.
34.(1)证明见解析;(2)不存在,理由见解析.
【分析】(1)根据正三棱锥的定义即可证明;
(2)利用反证法,由平面,假设存在这样的点,使得平面,推出平面平面,与平面和平面是相交平面矛盾,即可求解.
【详解】解:(1)证明:设,
则
∴是正三角形,
如图所示:连接,,
,
∴,,,
在中,由知:.
又平面,
,
∵,,
∴平面,
∴.
又平面,,
∴平面,
在线段上取点,使得,
则点是的重心,也就是的中心,
连接,则,
∴平面,
∴三棱锥是正三棱锥;
(2)∵平面与平面有公共点,
故平面与平面是相交平面,
∵,平面,平面,
∴平面,
假设存在这样的点,使得平面,
∵点与点不重合,
∴与是相交直线,
又平面,平面,且平面,平面,
∴平面平面,
这与平面和平面是相交平面矛盾,
∴不存在一点,使得平面.
35.(1)
(2)
【分析】(1)取中点,中点,分别连接,再根据,由向量垂直的数量积解出三边长度关系即可.
(2)取中点,在上取,在上取,分别连接,延长交于点,先根据解出三边长度关系,再证明出四边形是长方形得到的长度,最后在四面体中找到外接球球心的位置,且当外接球球心刚好与的外心重合时,外接球半径最小,体积也最小.
【详解】(1)取中点,中点,
分别连接,如图:
是的外心,是三条边上垂直平分线的交点,
,
则,
,
设,,,
则,
由余弦定理可得,
即,
令,解得,,
则.
故的余弦值为.
(2)取各边中点,连接成,如图:
则,且相似比为.
设是的外心,则,
由中位线平行底边可得,,
即是的垂心,由相似可得,即.
在上取,在上取,
分别连接,延长交于点,如图:
是的垂心,
,
又,
四边形是平行四边形.
则,
,
设,,,
则,
由余弦定理可得,
即,
令,解得,,
则,,
由正弦定理可得的外接圆半径,
.
,
又
,即,
所以,四边形是平行四边形,且为长方形,
在中,,
则.
在四面体中,设平面,且,
分别连接,如图:
由平面,可得,
设,
则,
,
当时,是四面体的外接球球心,是四面体的外接球半径,
解可得,
当四面体的外接球体积最小时,半径也最小,
而半径取最小值时,,
此时,解得,
则.
故当四面体外接球体积最小时,的值为.
【点睛】方法点睛:对于存在外接球的棱锥,求外接球球心位置的通用方法,即先找底面外接圆圆心,再过圆心作底面的垂线,则外接球球心一定在这条垂线上,再通过外接球球心到顶点的距离等于到底边图形顶点的距离,即可确定外接球球心的位置.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
