专题01 相交线与平行线(考点串讲)-七年级数学下学期期末考点大串讲(人教版)
文档属性
| 名称 | 专题01 相交线与平行线(考点串讲)-七年级数学下学期期末考点大串讲(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 10:41:07 | ||
图片预览





文档简介
(共64张PPT)
七年级人教版数学下册期末考点大串讲
串讲01 相交线与平行线
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
五大常考点:知识梳理+考点分类训练
五大重难点题型典例剖析+强化训练+四类期末重难点突破
四大易错易混经典例题+针对训练
5道期末真题对应考点练
考点透视
知识梳理
B
A
考点分类训练
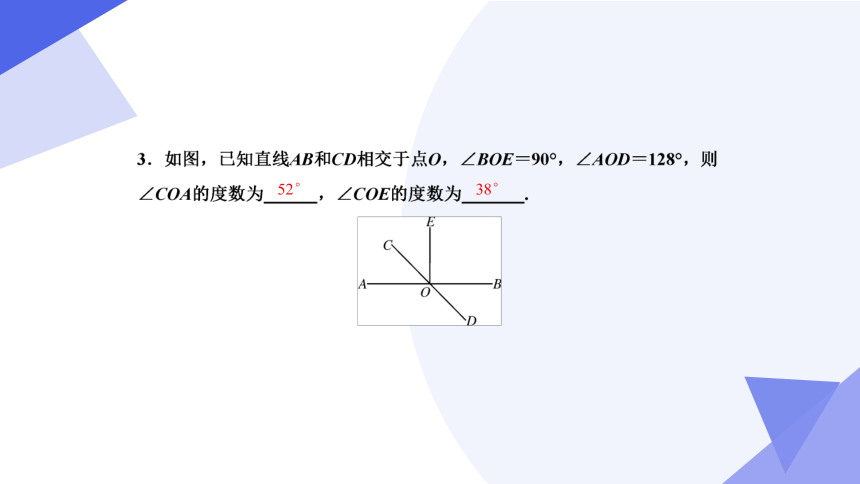
52°
38°
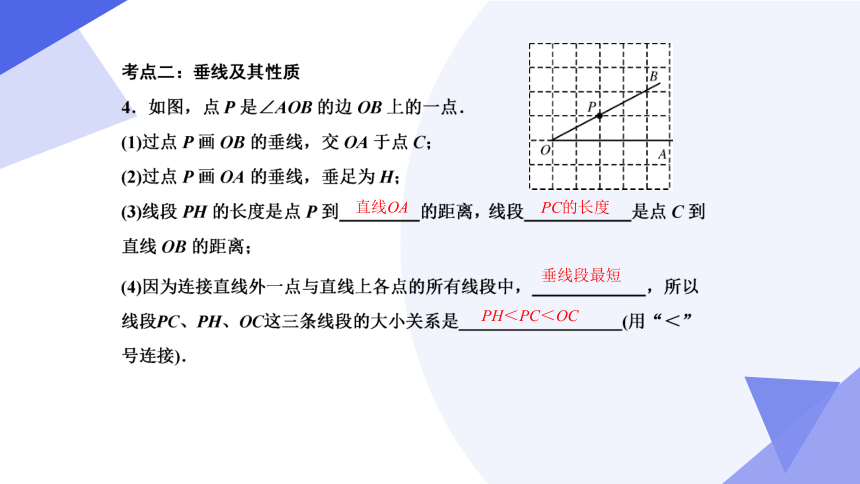
直线OA
PC的长度
垂线段最短
PH<PC<OC
C
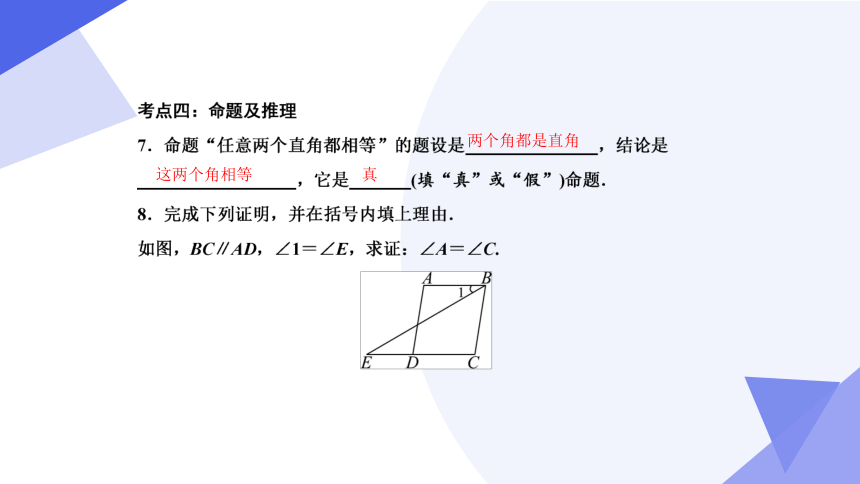
两个角都是直角
这两个角相等
真
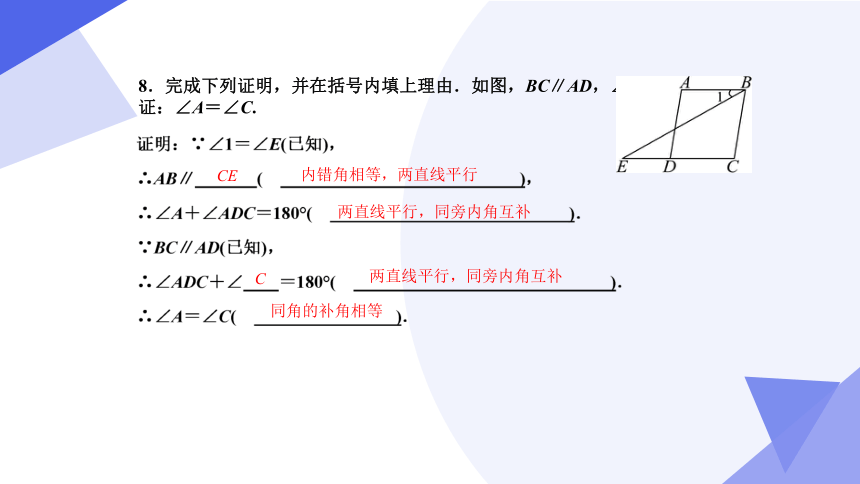
CE
内错角相等,两直线平行
两直线平行,同旁内角互补
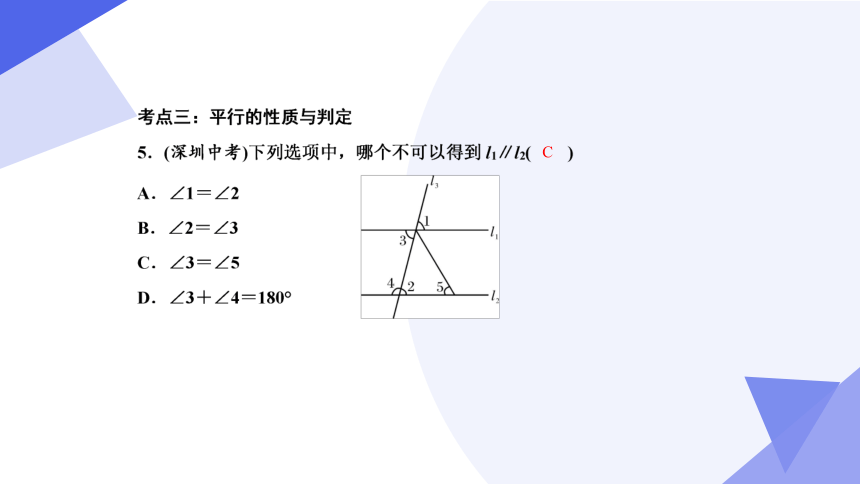
C
两直线平行,同旁内角互补
同角的补角相等
8.完成下列证明,并在括号内填上理由.如图,BC∥AD,∠1=∠E,求证:∠A=∠C.
D
D
重难点题型典例剖析
D
D
D
C
强化训练
A
B
80°
40
①②③⑤
D
期末重难点突破:平行线中的计算与说理
B
114°
200°
C
B
∠APC=∠PAB+∠PCD
∠APC+∠PAB+∠PCD
=360°
易错易混
易错点 2:理解不清对顶角、邻补角的概念而致错
例2.[2021湖南益阳资阳区校级月考]下列说法正确的是( )
A.相等的角是对顶角
B.邻补角一定互补
C.互补的两个角一定是邻补角
D.两个角不是对顶角,则这两个角不相等
【解析】A选项,相等的角不一定是对顶角,原说法错误,不符合题意;
B选项,邻补角一定互补,原说法正确,符合题意;
C选项,互补的两个角不一定是邻补角,原说法错误,不符合题意;
D选项,若两个角不是对顶角,则这两个角不一定相等,原说法错误,不符合题意.故选 B.
B
A
易错点4: 若同位角数量关系不清楚,则不能判断两条直线是否平行
例4.两直线被第三条直线所截,ㄥ1与∠2是同位角,则这两条直线( )
A.平行 B.相交 C.垂直 D.无法确定
【解析】因为同位角的数量关系不明确所以无法判断两条直线的位置关系.故选 D
D
1.如图,下列判定错误的是( ____ )
A.因为∠1=∠2,所以c∥d B.因为∠3=∠4,所以c∥d
C.因为∠1=∠3,所以a∥b D.因为∠1=∠4,所以a∥b
【解析】解:A. 因为∠1=∠2,所以c∥d(内错角相等,两直线平行),故本选
项正确;
B. 因为∠3=∠4,所以c∥d (同位角相等,两直线平行),故本选项正确;
C. 由∠1=∠3,不能得到a∥b,故本选项错误;
C
针对训练
D. 因为∠1=∠4,所以a∥b(内错角相等,两直线平行),故本选项正确;
故选:C.
2.下列图形中,由∠1=∠2能得到AB∥CD的是( ____ )
A.____ B.______
C._____ D._____
A
【解析】解:A、由∠1=∠2能得到AB∥CD,故A符合题意;
B、由∠1=∠2,不能得到AB∥CD,故B不符合题意;
C、由∠1=∠2能得到AD∥BC,故C不符合题意;
D、如图:____
∵∠2≠∠3,∠1=∠2,
∴∠1≠∠3,
∴不能得到AB∥CD,
故D不符合题意;故选:A.
3.如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( ____ )
A.∠1=∠2 B.∠D+∠DAB=180°
C.∠B=∠DCE D.∠3=∠4
【解析】解:A、根据内错角相等,两直线平行可判定AB∥CD,故此选项
不合题意;
B、根据同旁内角互补,两直线平行可判定AB∥CD,故此选项不合题意;
D
C、根据同位角相等,两直线平行可判定AB∥CD,故此选项不合题意;
D、根据内错角相等,两直线平行可判定AD∥CB,故此选项符合题意.
故选:D.
4.如图,四边形ABCD中,BD与AC相交于点O,AE∥CF,E、F在BD上,下列条件中能判断AB∥CD的是( ____ )
A.∠1=∠2 B.∠3=∠4
C.∠DAE=∠BCF D.∠BAD=∠DCB
【解析】解:A、∵AE∥CF,∴∠3=∠4,
∵∠1=∠2,∴∠1+∠3=∠4+∠2,∴∠BAO=∠DCO,∴AB∥CD,
故A符合题意;
B、∵∠3=∠4,∴AE∥CF,故B不符合题意;
C、∵AE∥CF,∴∠3=∠4,∵∠DAE=∠BCF,∴∠DAE-∠3=∠BCF-∠4,
∴∠DAC=∠ACB,∴AD∥CB,故C不符合题意;
D、∵AE∥CF,∴∠3=∠4,∵∠BAD=∠DCB,∴∠BAD-∠3=∠BCD-∠4,
∴∠1+∠CAD=∠2+∠ACB,∵∠1和∠2不一定相等,
∴∠BAC和∠ACD不一定相等,∴AB和CD不一定平行,故选D不符合题意;
故选:A.
A
5.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( ____ )
A.5个 B.4个 C.3个 D.2个
【解析】解:①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
C
④∵∠1=∠3,∴l1∥l2,故本条件符合题意;
⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:C.
6.如图,∠1和∠2是直线 ____ 与直线 ____ 被直线 ____ 所截得到的 _____ 角.∠1的内错角有 ____ 个,∠3 的同位角有 ____ 个.
【解析】解:如图:设直线a与直线d相交于点A,直线b与直线c相交于点B,直线a与直线b相交于点C,∠1和∠2是直线a与直线c被直线d所截得到的内错角.∠1的内错角是∠4和∠2,共有2个,∠3的同位角是∠5,∠6,∠7,∠ABC,共有4个,
故答案为:a;c;d;内错;2;4.
___
a
c
d
内错
2
4
7.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),当∠BAD= _____________ 时,CD∥AB.
【解析】解:如图所示:当CD∥AB时,
∠BAD=∠D=30°;
如图所示,当AB∥CD时,∠C=∠BAC=60°,
∴∠BAD=60°+90°=150°;
故答案为:150°或30°.
30°或150°
8.如图,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;⑤∠B=∠D.其中,一定能判定AB∥CD的条件有 _____ (填写所有正确的序号).
【解析】解:①∵∠B+∠BCD=180°,∴AB∥CD;
②∵∠1=∠2,∴AD∥CB;
③∵∠3=∠4,∴AB∥CD;
①③④
④∵∠B=∠5,∴AB∥CD,
⑤由∠B=∠D,不能判定AB∥CD;
故答案为:①③④.
9.如图所示,已知直线AB,CD相交于点O,且OE平分∠BOC
(1)∠AOC与 _______________ 互为邻补角;
(2)与∠EOA互为补角的是哪些角?试说明理由;
(3)若∠AOC=42°,求∠BOE的度数.
【解析】解:(1)由图形可知,∠AOC+∠BOC=∠AOC+∠AOD=180°;
∴∠AOC与∠BOC和∠AOD互为邻补角,故答案为:∠BOC和∠AOD.
(2)∠BOE和∠COE,理由如下:由图形可知,∠EOA+∠BOE=180°,
∵OE平分∠BOC,∴∠BOE=∠COE,
∴∠EOA+∠COE=180°,∴∠EOA的补角有∠BOE和∠COE.
(3)∵∠AOC=42°,∴∠BOC=180°-∠AOC=138°,
∵OE平分∠BOC,∴∠BOE= ∠BOC=69°.
∠BOC和∠AOD
10.如图,直线AB,CD相交于点O,∠1:∠2=2:3,求∠2和∠3的度数.
【解析】解:由图可知,∠1+∠2=180°,
∵∠1:∠2=2:3,
∴∠1=180°× =72°,∠2=180°× =108°,
∴∠3=∠1=72°.
11.观察下图,并解答下列问题:
_______
(1)图①中,有 ____ 条直线, ____ 对对顶角;
(2)图②中,有 ____ 条直线, ____ 对对顶角;
(3)图③中,有 ____ 条直线, ____ 对对顶角;
(4)猜想:当n条直线相交于一点时,可形成 _________ 对对顶角;(用含n的式子表示)
(5)若有100条直线相交于一点,则可形成 ______ 对对顶角.
2
2
3
6
4
12
n(n-1)
9900
【解析】解:(1)如图①,两条直线相交于一点,共有1×2=2对对顶角
故答案为:2;2;
(2)如图②,三条直线相交于一点,共有2×3=6对对顶角;
故答案为:3;6;
(3)如图③,四条直线相交于一点,共有3×4=12对对顶角;
故答案为:4;12;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,
若有n条直线相交于一点,则可形成n(n-1)对对顶角;
故答案为:n(n-1);
(5)若有100条直线相交于一点,则可形成(100-1)×100=9900对对顶角
故答案为:9900.
12.如图,已知∠A=∠D,∠C=∠F,那么CE与BF平行吗?为什么?
【解析】解:平行.理由如下:
∵∠A=∠D,
∴AC∥DF,
∴∠DEC=∠C,
又∵∠C=∠F
∴∠DEC=∠F,
∴BF∥CE.
1.(2023春·会同县期末)如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则( ____ )
A.乙比甲先到 B.甲比乙先到
C.甲和乙同时到 D.无法确定
【解析】解:∵甲、乙两只蚂蚁的行程相同,且两只蚂蚁的速度相同,
∴两只蚂蚁同时到达.
故选:C.
C
押题预测
2.(2023秋·思明区校级期末)如图所示,∠B与∠3是一对( ____ )
A.同位角 B.内错角
C.同旁内角 D.对顶角
【解析】解:∠B与∠3是直线DE和直线BC被直线AB所截得到的同旁内角,
故选:C.
C
3.(2023秋·沭阳县期末)如图,△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,P为直线AB上一动点,连接PC,则线段PC的最小值是( ____ )
A.3 B.2.5 C.2.4 D.2
【解析】解:在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,
∵当PC⊥AB时,PC的值最小,
此时:△ABC的面积= AB PC= AC BC,
∴5PC=3×4,
C
∴PC=2.4,
故选:C.
4.(2023春 清江浦区期末)探究问题:已知∠ABC,画一个角∠DEF,使DE∥AB,EF∥BC,且DE交BC于点P.∠ABC与∠DEF有怎样的数量关系?
______
(1)我们发现∠ABC与∠DEF有两种位置关系:如图1与图2所示.
①图1中∠ABC与∠DEF数量关系为 _____________________ ;图2中∠ABC与∠DEF数量关系为 ______________ ;
∠ABC+∠DEF=180°
∠ABC=∠DEF
请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述): ___________________________________________________________ .
(2)应用②中的真命题,解决以下问题:
若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
【解析】解:(1)①如图1中,∠ABC+∠DEF=180°.如图2中,∠ABC=∠DEF,
故答案为:∠ABC+∠DEF=180°,∠ABC=∠DEF.
理由:如图1中,
如果两个角的两边互相平行,那么这两个角相等或互补
∵BC∥EF,∴∠DPB=∠DEF,
∵AB∥DE,∴∠ABC+∠DPB=180°,
∴∠ABC+∠DEF=180°.
如图2中,∵BC∥EF,∴∠DPC=∠DEF,
∵AB∥DE,∴∠ABC=∠DPC,∴∠ABC=∠DEF.
②结论:如果两个角的两边互相平行,那么这两个角相等或互补.
故答案为:如果两个角的两边互相平行,那么这两个角相等或互补.
(2)设两个角分别为x和2x-30°,
由题意x=2x-30°或x+2x-30°=180°,
解得x=30°或x=70°,
∴这两个角的度数为30°,30°或70°和110°.
5.(2023春 岳池县校级期末)如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
【解析】(1)证明:∵∠CED=∠GHD,
∴CE∥GF;
(2)解:∵CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠DHG=∠EHF=100°,∠D=30°,
∴∠CGF=100°+30°=130°,
∵CE∥GF,
∴∠C=180°-130°=50°,
∵AB∥CD,
∴∠AEC=50°,
∴∠AEM=180°-50°=130°.
七年级人教版数学下册期末考点大串讲
串讲01 相交线与平行线
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
五大常考点:知识梳理+考点分类训练
五大重难点题型典例剖析+强化训练+四类期末重难点突破
四大易错易混经典例题+针对训练
5道期末真题对应考点练
考点透视
知识梳理
B
A
考点分类训练
52°
38°
直线OA
PC的长度
垂线段最短
PH<PC<OC
C
两个角都是直角
这两个角相等
真
CE
内错角相等,两直线平行
两直线平行,同旁内角互补
C
两直线平行,同旁内角互补
同角的补角相等
8.完成下列证明,并在括号内填上理由.如图,BC∥AD,∠1=∠E,求证:∠A=∠C.
D
D
重难点题型典例剖析
D
D
D
C
强化训练
A
B
80°
40
①②③⑤
D
期末重难点突破:平行线中的计算与说理
B
114°
200°
C
B
∠APC=∠PAB+∠PCD
∠APC+∠PAB+∠PCD
=360°
易错易混
易错点 2:理解不清对顶角、邻补角的概念而致错
例2.[2021湖南益阳资阳区校级月考]下列说法正确的是( )
A.相等的角是对顶角
B.邻补角一定互补
C.互补的两个角一定是邻补角
D.两个角不是对顶角,则这两个角不相等
【解析】A选项,相等的角不一定是对顶角,原说法错误,不符合题意;
B选项,邻补角一定互补,原说法正确,符合题意;
C选项,互补的两个角不一定是邻补角,原说法错误,不符合题意;
D选项,若两个角不是对顶角,则这两个角不一定相等,原说法错误,不符合题意.故选 B.
B
A
易错点4: 若同位角数量关系不清楚,则不能判断两条直线是否平行
例4.两直线被第三条直线所截,ㄥ1与∠2是同位角,则这两条直线( )
A.平行 B.相交 C.垂直 D.无法确定
【解析】因为同位角的数量关系不明确所以无法判断两条直线的位置关系.故选 D
D
1.如图,下列判定错误的是( ____ )
A.因为∠1=∠2,所以c∥d B.因为∠3=∠4,所以c∥d
C.因为∠1=∠3,所以a∥b D.因为∠1=∠4,所以a∥b
【解析】解:A. 因为∠1=∠2,所以c∥d(内错角相等,两直线平行),故本选
项正确;
B. 因为∠3=∠4,所以c∥d (同位角相等,两直线平行),故本选项正确;
C. 由∠1=∠3,不能得到a∥b,故本选项错误;
C
针对训练
D. 因为∠1=∠4,所以a∥b(内错角相等,两直线平行),故本选项正确;
故选:C.
2.下列图形中,由∠1=∠2能得到AB∥CD的是( ____ )
A.____ B.______
C._____ D._____
A
【解析】解:A、由∠1=∠2能得到AB∥CD,故A符合题意;
B、由∠1=∠2,不能得到AB∥CD,故B不符合题意;
C、由∠1=∠2能得到AD∥BC,故C不符合题意;
D、如图:____
∵∠2≠∠3,∠1=∠2,
∴∠1≠∠3,
∴不能得到AB∥CD,
故D不符合题意;故选:A.
3.如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( ____ )
A.∠1=∠2 B.∠D+∠DAB=180°
C.∠B=∠DCE D.∠3=∠4
【解析】解:A、根据内错角相等,两直线平行可判定AB∥CD,故此选项
不合题意;
B、根据同旁内角互补,两直线平行可判定AB∥CD,故此选项不合题意;
D
C、根据同位角相等,两直线平行可判定AB∥CD,故此选项不合题意;
D、根据内错角相等,两直线平行可判定AD∥CB,故此选项符合题意.
故选:D.
4.如图,四边形ABCD中,BD与AC相交于点O,AE∥CF,E、F在BD上,下列条件中能判断AB∥CD的是( ____ )
A.∠1=∠2 B.∠3=∠4
C.∠DAE=∠BCF D.∠BAD=∠DCB
【解析】解:A、∵AE∥CF,∴∠3=∠4,
∵∠1=∠2,∴∠1+∠3=∠4+∠2,∴∠BAO=∠DCO,∴AB∥CD,
故A符合题意;
B、∵∠3=∠4,∴AE∥CF,故B不符合题意;
C、∵AE∥CF,∴∠3=∠4,∵∠DAE=∠BCF,∴∠DAE-∠3=∠BCF-∠4,
∴∠DAC=∠ACB,∴AD∥CB,故C不符合题意;
D、∵AE∥CF,∴∠3=∠4,∵∠BAD=∠DCB,∴∠BAD-∠3=∠BCD-∠4,
∴∠1+∠CAD=∠2+∠ACB,∵∠1和∠2不一定相等,
∴∠BAC和∠ACD不一定相等,∴AB和CD不一定平行,故选D不符合题意;
故选:A.
A
5.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( ____ )
A.5个 B.4个 C.3个 D.2个
【解析】解:①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
C
④∵∠1=∠3,∴l1∥l2,故本条件符合题意;
⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:C.
6.如图,∠1和∠2是直线 ____ 与直线 ____ 被直线 ____ 所截得到的 _____ 角.∠1的内错角有 ____ 个,∠3 的同位角有 ____ 个.
【解析】解:如图:设直线a与直线d相交于点A,直线b与直线c相交于点B,直线a与直线b相交于点C,∠1和∠2是直线a与直线c被直线d所截得到的内错角.∠1的内错角是∠4和∠2,共有2个,∠3的同位角是∠5,∠6,∠7,∠ABC,共有4个,
故答案为:a;c;d;内错;2;4.
___
a
c
d
内错
2
4
7.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),当∠BAD= _____________ 时,CD∥AB.
【解析】解:如图所示:当CD∥AB时,
∠BAD=∠D=30°;
如图所示,当AB∥CD时,∠C=∠BAC=60°,
∴∠BAD=60°+90°=150°;
故答案为:150°或30°.
30°或150°
8.如图,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;⑤∠B=∠D.其中,一定能判定AB∥CD的条件有 _____ (填写所有正确的序号).
【解析】解:①∵∠B+∠BCD=180°,∴AB∥CD;
②∵∠1=∠2,∴AD∥CB;
③∵∠3=∠4,∴AB∥CD;
①③④
④∵∠B=∠5,∴AB∥CD,
⑤由∠B=∠D,不能判定AB∥CD;
故答案为:①③④.
9.如图所示,已知直线AB,CD相交于点O,且OE平分∠BOC
(1)∠AOC与 _______________ 互为邻补角;
(2)与∠EOA互为补角的是哪些角?试说明理由;
(3)若∠AOC=42°,求∠BOE的度数.
【解析】解:(1)由图形可知,∠AOC+∠BOC=∠AOC+∠AOD=180°;
∴∠AOC与∠BOC和∠AOD互为邻补角,故答案为:∠BOC和∠AOD.
(2)∠BOE和∠COE,理由如下:由图形可知,∠EOA+∠BOE=180°,
∵OE平分∠BOC,∴∠BOE=∠COE,
∴∠EOA+∠COE=180°,∴∠EOA的补角有∠BOE和∠COE.
(3)∵∠AOC=42°,∴∠BOC=180°-∠AOC=138°,
∵OE平分∠BOC,∴∠BOE= ∠BOC=69°.
∠BOC和∠AOD
10.如图,直线AB,CD相交于点O,∠1:∠2=2:3,求∠2和∠3的度数.
【解析】解:由图可知,∠1+∠2=180°,
∵∠1:∠2=2:3,
∴∠1=180°× =72°,∠2=180°× =108°,
∴∠3=∠1=72°.
11.观察下图,并解答下列问题:
_______
(1)图①中,有 ____ 条直线, ____ 对对顶角;
(2)图②中,有 ____ 条直线, ____ 对对顶角;
(3)图③中,有 ____ 条直线, ____ 对对顶角;
(4)猜想:当n条直线相交于一点时,可形成 _________ 对对顶角;(用含n的式子表示)
(5)若有100条直线相交于一点,则可形成 ______ 对对顶角.
2
2
3
6
4
12
n(n-1)
9900
【解析】解:(1)如图①,两条直线相交于一点,共有1×2=2对对顶角
故答案为:2;2;
(2)如图②,三条直线相交于一点,共有2×3=6对对顶角;
故答案为:3;6;
(3)如图③,四条直线相交于一点,共有3×4=12对对顶角;
故答案为:4;12;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,
若有n条直线相交于一点,则可形成n(n-1)对对顶角;
故答案为:n(n-1);
(5)若有100条直线相交于一点,则可形成(100-1)×100=9900对对顶角
故答案为:9900.
12.如图,已知∠A=∠D,∠C=∠F,那么CE与BF平行吗?为什么?
【解析】解:平行.理由如下:
∵∠A=∠D,
∴AC∥DF,
∴∠DEC=∠C,
又∵∠C=∠F
∴∠DEC=∠F,
∴BF∥CE.
1.(2023春·会同县期末)如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则( ____ )
A.乙比甲先到 B.甲比乙先到
C.甲和乙同时到 D.无法确定
【解析】解:∵甲、乙两只蚂蚁的行程相同,且两只蚂蚁的速度相同,
∴两只蚂蚁同时到达.
故选:C.
C
押题预测
2.(2023秋·思明区校级期末)如图所示,∠B与∠3是一对( ____ )
A.同位角 B.内错角
C.同旁内角 D.对顶角
【解析】解:∠B与∠3是直线DE和直线BC被直线AB所截得到的同旁内角,
故选:C.
C
3.(2023秋·沭阳县期末)如图,△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,P为直线AB上一动点,连接PC,则线段PC的最小值是( ____ )
A.3 B.2.5 C.2.4 D.2
【解析】解:在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,
∵当PC⊥AB时,PC的值最小,
此时:△ABC的面积= AB PC= AC BC,
∴5PC=3×4,
C
∴PC=2.4,
故选:C.
4.(2023春 清江浦区期末)探究问题:已知∠ABC,画一个角∠DEF,使DE∥AB,EF∥BC,且DE交BC于点P.∠ABC与∠DEF有怎样的数量关系?
______
(1)我们发现∠ABC与∠DEF有两种位置关系:如图1与图2所示.
①图1中∠ABC与∠DEF数量关系为 _____________________ ;图2中∠ABC与∠DEF数量关系为 ______________ ;
∠ABC+∠DEF=180°
∠ABC=∠DEF
请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述): ___________________________________________________________ .
(2)应用②中的真命题,解决以下问题:
若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
【解析】解:(1)①如图1中,∠ABC+∠DEF=180°.如图2中,∠ABC=∠DEF,
故答案为:∠ABC+∠DEF=180°,∠ABC=∠DEF.
理由:如图1中,
如果两个角的两边互相平行,那么这两个角相等或互补
∵BC∥EF,∴∠DPB=∠DEF,
∵AB∥DE,∴∠ABC+∠DPB=180°,
∴∠ABC+∠DEF=180°.
如图2中,∵BC∥EF,∴∠DPC=∠DEF,
∵AB∥DE,∴∠ABC=∠DPC,∴∠ABC=∠DEF.
②结论:如果两个角的两边互相平行,那么这两个角相等或互补.
故答案为:如果两个角的两边互相平行,那么这两个角相等或互补.
(2)设两个角分别为x和2x-30°,
由题意x=2x-30°或x+2x-30°=180°,
解得x=30°或x=70°,
∴这两个角的度数为30°,30°或70°和110°.
5.(2023春 岳池县校级期末)如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
【解析】(1)证明:∵∠CED=∠GHD,
∴CE∥GF;
(2)解:∵CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠DHG=∠EHF=100°,∠D=30°,
∴∠CGF=100°+30°=130°,
∵CE∥GF,
∴∠C=180°-130°=50°,
∵AB∥CD,
∴∠AEC=50°,
∴∠AEM=180°-50°=130°.
同课章节目录
