专题03 平行四边形(考点串讲)-八年级数学下学期期末考点大串讲(人教版)
文档属性
| 名称 | 专题03 平行四边形(考点串讲)-八年级数学下学期期末考点大串讲(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 09:01:04 | ||
图片预览







文档简介
(共54张PPT)
八年级人教版数学下册期末考点大串讲
串讲03 平行四边形
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
六大易错易混经典例题+针对训练
5道期末真题对应考点练
两大重难点题型典例剖析+强化训练+两类期末重难点突破
三大常考点:知识梳理+考点分类训练
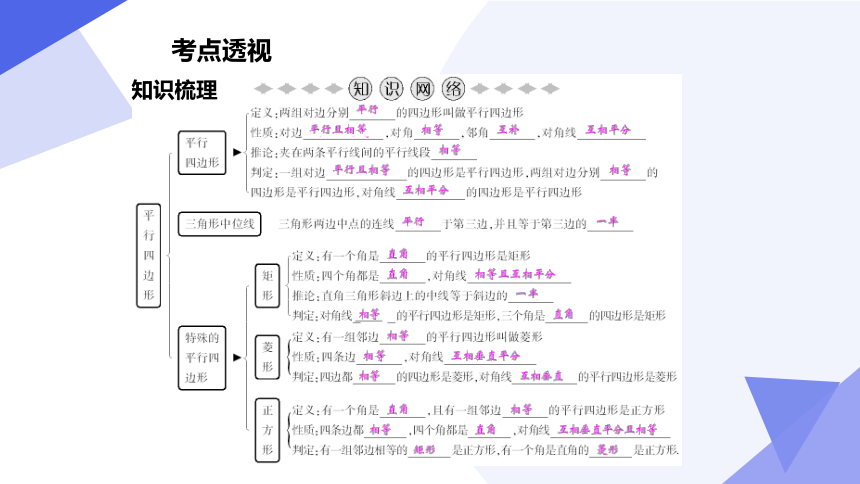
考点透视
知识梳理
A
C
考点分类训练
不唯一,如DE=EC
32cm或34cm
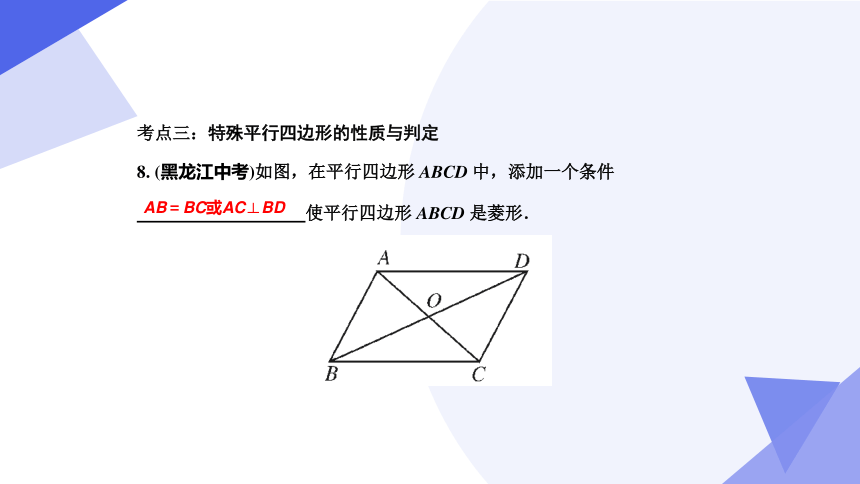
C
AB=BC或AC⊥BD
A
重难点题型典例剖析
B
C
强化训练
B
5
12
期末重难点突破:平行四边形
B
易错易混
B
C
(3,2)或(-3,2)或(5,-2)
针对训练
易错点一 解决无图的计算问题时,未分类讨论
例1在中,∠BAD的平分线AE把边BC的长分成5和6两部分,求的周长.
①当BE=5,EC=6时,
的周长为2(AB+BC)=2×(5+5+6)= 32;
②当BE=6,EC=5时,
的周长为2(AB+BC)=2×(6+6+5)= 34.
故的周长为 32 或 34.
易错点二 图形误导,错用条件
例2.如图,在ABCD中,对角线AC,BD相交于点O,OE⊥AD,OF⊥BC,垂足分别是E,F.求证OE=OF.
∵OE⊥AD, OF⊥BC,
∴∠DEO = ∠BFO = 90°.
∴ ΔDOE≌ΔBOF(AAS).
∴OE=OF.
易错点三 混用矩形的判定方法
例3.下列说法中正确的是( )
A.一个角是直角,两条对角线相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.一个角是直角且对角线互相平分的四边形是矩形
正解:
一个角是直角,两条对角线相等的四边形,有可能是一般的四边形,故A错误;一组对边平行且有一个角是直角的四边形,有可能是一般的四边形,故B错误;对角线互相垂直的平行四边形是菱形,故C错误;对角线互相平分的四边形是平行四边形,有一个角是直角的平行四边形是矩形,故D正确.故选D.
D
易错点四 菱形判定的误区
例4.如图,下列条件:①AC⊥BD,OC=OA;②∠1=∠2=∠3=∠4;③OA=OC,OB=OD,AC⊥BD;④AB=BC=CD,AC⊥BD.其中,一定能判定四边形ABCD为菱形的有( )
A.1 个 B.2 个 C.3 个 D.4 个
正解:
①当 AC⊥BD,OC=OA时,不能确定 BO 是否等于DO,故不能判定四边形ABCD为菱形;②可利用有一组邻边相等的平行四边形是菱形进行判定;③可利用对角线互相垂直的平行四边形是菱形进行判定;④可利用四条边相等的四边形是菱形进行判定.故选 C.
易错点五 正方形判定的误区
例5.下列命题:①对角线相等的菱形是正方形;②对角线相等且互相垂直的四边形是正方形;③一组邻边相等且对角线相等的四边形是正方形;④四边都相等,四角都相等的四边形是正方形.其中正确的有( )
正解:对角线相等的菱形是正方形,故①正确;对角线相等且互相垂直平分的四边形是正方形,故②错误;一组邻边相等且对角线相等的平行四边形是正方形,故③错误;四边都相等,可判定是菱形,四角都相等,可判定是矩形,故④正确.故选 C.
A.4 个 B.3个 C.2个 D.1个
C
易错点六 对图形的考虑不全面
例6.[邵阳邵东市期末]如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),D是OA的中点,点P在BC上运动,当△ODP是以OD为腰的等腰三角形时,点P的坐标为 .
正解:∵四边形OABC为矩形,A(10,0),C(0,4),
∵BC=0A=10,AB=OC=4.∵D是OA的中点,∴OD=AD=5.
①当O是顶角顶点时,OP=OD=5.
在Rt△OPC中,CP=,点P的坐标是(3,4).
(3,4)
易错点六 对图形的考虑不全面
例6.[邵阳邵东市期末]如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),D是OA的中点,点P在BC上运动,当△ODP是以OD为腰的等腰三角形时,点P的坐标为 .
(3,4)或(2,4)或(8,4)
②当D是顶角顶点时,PD=OD=5.
如图,过点D作DM⊥BC于点 M.
在 Rt△PDM 中,.
当点P在点M的左侧时,CP=5-3=2,∴点P的坐标是(2,4);
当点P'在点M的右侧时,CP'=5+3=8,∴点P'的坐标是(8,4).
综上所述,点P的坐标为(3,4)或(2,4)或(8,4).
故答案为(3,4)或(2,4)或(8,4).
1.(2023春·武汉期末下列条件中,不能判定四边形ABCD是平行
四边形的是( ____ )
A.AB=CD,BC=AD B.∠A=∠C,∠B=∠D
C.AB∥CD,BC=AD D.AB∥CD,AB=CD
【解析】解:A、∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,故选项A不符合题意;
B、∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,故选项B不符合题意;
C、AB∥CD,BC=AD,不能判定四边形ABCD是平行四边形,
故选项C符合题意;
D、∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,故选项D不符合题意;故选:C.
C
押题预测
2.(2023春·辛集市期末 )如图, ABCD中,AB=22cm,BC=8 cm,∠A=45°,动点E从A出发,以2cm/s的速度沿AB向点B运动,动点F从点C出发,以1cm/s的速度沿着CD向D运动,当点E到达点B时,两个点同时停止.则EF的长为10cm时点E的运动时间是( ____ )
A.6s B.6s或10s
C.8s D.8s或12s
【解析】解:在 ABCD中,CD=AB=22cm,AD=BC=8 cm,
如图,过点D作DG⊥AB于点G,
∵∠A=45°,∴△ADG是等腰直角三角形,∴AG=DG= AD=8,
过点F作FH⊥AB于点H,得矩形DGHF,∴DG=FH=8cm,DF=GH,
∵EF=10cm,∴EH= =6cm,
由题意可知:AE=2t cm,CF=t cm,∴GE=AE=AG=(2t-8)cm,DF=CD-CF=(22-t)cm,
∴GH=GE+EH=(2t-8)+6=(2t-2)cm,∴2t-2=22-t,解得t=8,
C
当F点在E点左侧时,由题意可知:AE=2t cm,CF=t cm,
∴GE=AE-AG=(2t-8)cm,DF=CD-CF=(22-t)cm,
∴GH=GE-EH=(2t-8)-6=(2t-14)cm,
∴2t-14=22-t,
解得t=12,
∵点E到达点B时,两点同时停止运动,
∴2t≤22,解得t≤11.
∴t=12不符合题意,舍去,
∴EF的长为10cm时点E的运动时间是8s,
故选:C.
3.(2023春·益阳期末 )如图,在Rt△BAC和Rt△BDC中,∠BAC=∠BDC=90°,O是BC的中点,连接AO、DO.若AO=3,则DO的长为 ____ .
【解析】解:在Rt△BAC和Rt△BDC中,∵∠BAC=∠BDC=90°,O是BC的中点,
∴AO= BC,DO= BC,∴DO=AO,
∵AO=3,∴DO=3,故答案为3.
3
4.(2023春·梁园区期末)已知在△ABC中,AC=6cm,点D、E分别是AC、BC的中点,连接DE,在DE上有一点F,EF=1cm,连接AF,CF,若AF⊥CF,则AB= _____ .
【解析】解:在Rt△AFC中,点D是AC的中点,AC=6cm,
∴DF= AC= ×6=3(cm),
∵EF=1cm,∴DE=DF+EF=3+1=4(cm),
∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,∴AB=2DE=2×4=8(cm),
故答案为:8cm.
8cm
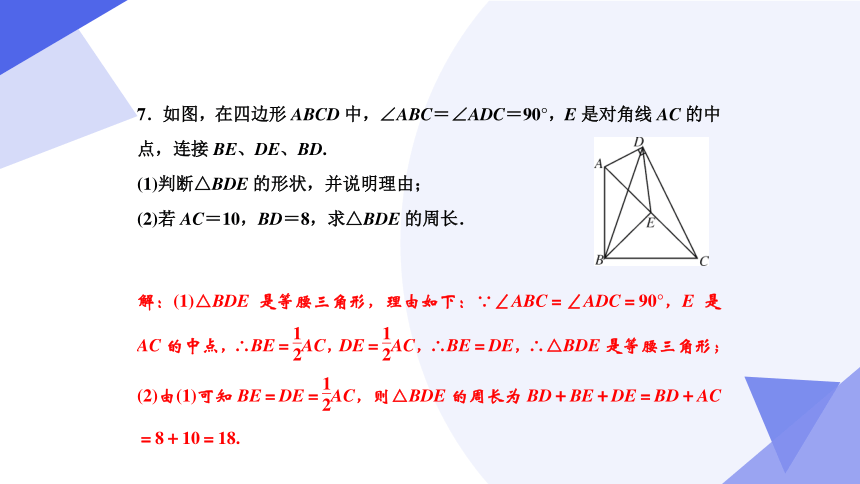
5.(2023春·西乡塘区校级期末)【问题原型】如图1,在四边形ABCD中,∠ADC=90°,AB=AC.点E、F分别为AC、BC的中点,连接EF,DE.试说明:DE=EF.
【探究】如图2,在问题原型的条件下,当AC平分∠BAD,∠DEF=90°时,求∠BAD的大小.
【应用】如图3,在问题原型的条件下,当AB=2,且四边形CDEF是菱形时,直接写出四边形ABCD的面积._______
【解析】解:【问题原型】证明:
在△ABC中,点E,F分别为AC,BC的中点
∴EF∥AB,且EF= AB
在Rt△ACD中,点E为AC的中点∴DE= AC∵AB=AC,∴DE=EF
【探究】解:∵AC平分∠BAD,EF∥AB,
DE= AC=AE=EC
∴∠BAC=∠DAC,∠CEF=∠BAC
∠DEC=2∠DAC=∠BAD
∵∠DEF=90°∴∠CEF+∠DEC=∠BAC+2∠DAC=90°
∴∠BAC=∠DAC=30°,
∴∠BAD=60°
【应用】四边形ABCD的面积为:
∵四边形CDEF是菱形,EC=DE,
∴△CDE与△CEF都是等边三角形,
∵AB=2,∴EF=DE=CD=CF=1
∴S△DCE=S△DEA=S△CEF= ,
∵EF∥AB,∴ ,∴S△ABC=4S△CEF=
∴S四边形ABCD=S△DCE+S△DEA+S△ABC
=2× + = .
八年级人教版数学下册期末考点大串讲
串讲03 平行四边形
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
六大易错易混经典例题+针对训练
5道期末真题对应考点练
两大重难点题型典例剖析+强化训练+两类期末重难点突破
三大常考点:知识梳理+考点分类训练
考点透视
知识梳理
A
C
考点分类训练
不唯一,如DE=EC
32cm或34cm
C
AB=BC或AC⊥BD
A
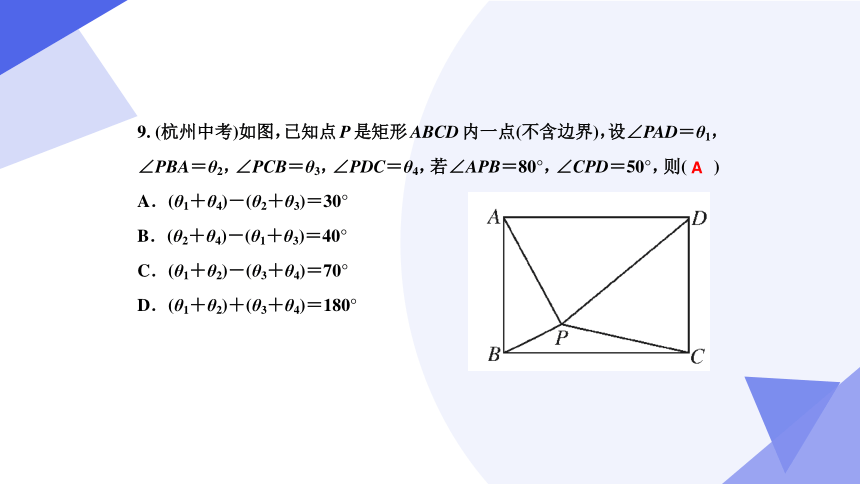
重难点题型典例剖析
B
C
强化训练
B
5
12
期末重难点突破:平行四边形
B
易错易混
B
C
(3,2)或(-3,2)或(5,-2)
针对训练
易错点一 解决无图的计算问题时,未分类讨论
例1在中,∠BAD的平分线AE把边BC的长分成5和6两部分,求的周长.
①当BE=5,EC=6时,
的周长为2(AB+BC)=2×(5+5+6)= 32;
②当BE=6,EC=5时,
的周长为2(AB+BC)=2×(6+6+5)= 34.
故的周长为 32 或 34.
易错点二 图形误导,错用条件
例2.如图,在ABCD中,对角线AC,BD相交于点O,OE⊥AD,OF⊥BC,垂足分别是E,F.求证OE=OF.
∵OE⊥AD, OF⊥BC,
∴∠DEO = ∠BFO = 90°.
∴ ΔDOE≌ΔBOF(AAS).
∴OE=OF.
易错点三 混用矩形的判定方法
例3.下列说法中正确的是( )
A.一个角是直角,两条对角线相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.一个角是直角且对角线互相平分的四边形是矩形
正解:
一个角是直角,两条对角线相等的四边形,有可能是一般的四边形,故A错误;一组对边平行且有一个角是直角的四边形,有可能是一般的四边形,故B错误;对角线互相垂直的平行四边形是菱形,故C错误;对角线互相平分的四边形是平行四边形,有一个角是直角的平行四边形是矩形,故D正确.故选D.
D
易错点四 菱形判定的误区
例4.如图,下列条件:①AC⊥BD,OC=OA;②∠1=∠2=∠3=∠4;③OA=OC,OB=OD,AC⊥BD;④AB=BC=CD,AC⊥BD.其中,一定能判定四边形ABCD为菱形的有( )
A.1 个 B.2 个 C.3 个 D.4 个
正解:
①当 AC⊥BD,OC=OA时,不能确定 BO 是否等于DO,故不能判定四边形ABCD为菱形;②可利用有一组邻边相等的平行四边形是菱形进行判定;③可利用对角线互相垂直的平行四边形是菱形进行判定;④可利用四条边相等的四边形是菱形进行判定.故选 C.
易错点五 正方形判定的误区
例5.下列命题:①对角线相等的菱形是正方形;②对角线相等且互相垂直的四边形是正方形;③一组邻边相等且对角线相等的四边形是正方形;④四边都相等,四角都相等的四边形是正方形.其中正确的有( )
正解:对角线相等的菱形是正方形,故①正确;对角线相等且互相垂直平分的四边形是正方形,故②错误;一组邻边相等且对角线相等的平行四边形是正方形,故③错误;四边都相等,可判定是菱形,四角都相等,可判定是矩形,故④正确.故选 C.
A.4 个 B.3个 C.2个 D.1个
C
易错点六 对图形的考虑不全面
例6.[邵阳邵东市期末]如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),D是OA的中点,点P在BC上运动,当△ODP是以OD为腰的等腰三角形时,点P的坐标为 .
正解:∵四边形OABC为矩形,A(10,0),C(0,4),
∵BC=0A=10,AB=OC=4.∵D是OA的中点,∴OD=AD=5.
①当O是顶角顶点时,OP=OD=5.
在Rt△OPC中,CP=,点P的坐标是(3,4).
(3,4)
易错点六 对图形的考虑不全面
例6.[邵阳邵东市期末]如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),D是OA的中点,点P在BC上运动,当△ODP是以OD为腰的等腰三角形时,点P的坐标为 .
(3,4)或(2,4)或(8,4)
②当D是顶角顶点时,PD=OD=5.
如图,过点D作DM⊥BC于点 M.
在 Rt△PDM 中,.
当点P在点M的左侧时,CP=5-3=2,∴点P的坐标是(2,4);
当点P'在点M的右侧时,CP'=5+3=8,∴点P'的坐标是(8,4).
综上所述,点P的坐标为(3,4)或(2,4)或(8,4).
故答案为(3,4)或(2,4)或(8,4).
1.(2023春·武汉期末下列条件中,不能判定四边形ABCD是平行
四边形的是( ____ )
A.AB=CD,BC=AD B.∠A=∠C,∠B=∠D
C.AB∥CD,BC=AD D.AB∥CD,AB=CD
【解析】解:A、∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,故选项A不符合题意;
B、∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,故选项B不符合题意;
C、AB∥CD,BC=AD,不能判定四边形ABCD是平行四边形,
故选项C符合题意;
D、∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,故选项D不符合题意;故选:C.
C
押题预测
2.(2023春·辛集市期末 )如图, ABCD中,AB=22cm,BC=8 cm,∠A=45°,动点E从A出发,以2cm/s的速度沿AB向点B运动,动点F从点C出发,以1cm/s的速度沿着CD向D运动,当点E到达点B时,两个点同时停止.则EF的长为10cm时点E的运动时间是( ____ )
A.6s B.6s或10s
C.8s D.8s或12s
【解析】解:在 ABCD中,CD=AB=22cm,AD=BC=8 cm,
如图,过点D作DG⊥AB于点G,
∵∠A=45°,∴△ADG是等腰直角三角形,∴AG=DG= AD=8,
过点F作FH⊥AB于点H,得矩形DGHF,∴DG=FH=8cm,DF=GH,
∵EF=10cm,∴EH= =6cm,
由题意可知:AE=2t cm,CF=t cm,∴GE=AE=AG=(2t-8)cm,DF=CD-CF=(22-t)cm,
∴GH=GE+EH=(2t-8)+6=(2t-2)cm,∴2t-2=22-t,解得t=8,
C
当F点在E点左侧时,由题意可知:AE=2t cm,CF=t cm,
∴GE=AE-AG=(2t-8)cm,DF=CD-CF=(22-t)cm,
∴GH=GE-EH=(2t-8)-6=(2t-14)cm,
∴2t-14=22-t,
解得t=12,
∵点E到达点B时,两点同时停止运动,
∴2t≤22,解得t≤11.
∴t=12不符合题意,舍去,
∴EF的长为10cm时点E的运动时间是8s,
故选:C.
3.(2023春·益阳期末 )如图,在Rt△BAC和Rt△BDC中,∠BAC=∠BDC=90°,O是BC的中点,连接AO、DO.若AO=3,则DO的长为 ____ .
【解析】解:在Rt△BAC和Rt△BDC中,∵∠BAC=∠BDC=90°,O是BC的中点,
∴AO= BC,DO= BC,∴DO=AO,
∵AO=3,∴DO=3,故答案为3.
3
4.(2023春·梁园区期末)已知在△ABC中,AC=6cm,点D、E分别是AC、BC的中点,连接DE,在DE上有一点F,EF=1cm,连接AF,CF,若AF⊥CF,则AB= _____ .
【解析】解:在Rt△AFC中,点D是AC的中点,AC=6cm,
∴DF= AC= ×6=3(cm),
∵EF=1cm,∴DE=DF+EF=3+1=4(cm),
∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,∴AB=2DE=2×4=8(cm),
故答案为:8cm.
8cm
5.(2023春·西乡塘区校级期末)【问题原型】如图1,在四边形ABCD中,∠ADC=90°,AB=AC.点E、F分别为AC、BC的中点,连接EF,DE.试说明:DE=EF.
【探究】如图2,在问题原型的条件下,当AC平分∠BAD,∠DEF=90°时,求∠BAD的大小.
【应用】如图3,在问题原型的条件下,当AB=2,且四边形CDEF是菱形时,直接写出四边形ABCD的面积._______
【解析】解:【问题原型】证明:
在△ABC中,点E,F分别为AC,BC的中点
∴EF∥AB,且EF= AB
在Rt△ACD中,点E为AC的中点∴DE= AC∵AB=AC,∴DE=EF
【探究】解:∵AC平分∠BAD,EF∥AB,
DE= AC=AE=EC
∴∠BAC=∠DAC,∠CEF=∠BAC
∠DEC=2∠DAC=∠BAD
∵∠DEF=90°∴∠CEF+∠DEC=∠BAC+2∠DAC=90°
∴∠BAC=∠DAC=30°,
∴∠BAD=60°
【应用】四边形ABCD的面积为:
∵四边形CDEF是菱形,EC=DE,
∴△CDE与△CEF都是等边三角形,
∵AB=2,∴EF=DE=CD=CF=1
∴S△DCE=S△DEA=S△CEF= ,
∵EF∥AB,∴ ,∴S△ABC=4S△CEF=
∴S四边形ABCD=S△DCE+S△DEA+S△ABC
=2× + = .
同课章节目录
