专题04 一次函数(考点串讲)-八年级数学下学期期末考点大串讲(人教版)
文档属性
| 名称 | 专题04 一次函数(考点串讲)-八年级数学下学期期末考点大串讲(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 09:01:14 | ||
图片预览









文档简介
(共59张PPT)
八年级人教版数学下册期末考点大串讲
串讲04 一次函数
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
五大易错易混经典例题+针对训练
5道期末真题对应考点练
四大重难点题型典例剖析+强化训练+三类期末重难点突破
四大常考点:知识梳理+考点分类训练
考点透视
知识梳理
C
考点分类训练
A
C
B
D
D
重难点题型典例剖析
B
D
A
C
强化训练
B
B
三、四
-4≤m≤4
200
B
期末重难点突破:一次函数
x>3
D
D
A
a≤3
易错易混
-1<x<2
针对训练
易错点一 不能正确理解函数的概念而出错
例1.[萍乡期末]下列关系式中,y不是x的函数的是( )
正解:在|y|=x中,x取一个非零的值,有两个y值与其对应,所以y不是x的函数.故选D.
D
易错点二 画函数图象时,忽略自变量的取值范围而出错
例2.拖拉机刚开始工作时,油箱中有40L油,且工作时每小时耗油5L.
(1)写出拖拉机油箱中的余油量Q(单位:L)关于工作时间t(单位:h)的函数解析式;
(2)求出自变量t的取值范围;
(3)画出这个函数的图象.
解:
(1)由题意可知Q=40-5t.
(2)因为油箱中有40L油,且工作时每小时耗油5L,
所以,
则自变量t的取值范围是.
正解:(3)当t=0 时,Q=40;
当t=8 时,Q=0.在平面直角坐标系中找到两点,
作线段即可,如图所示.
易错点二 画函数图象时,忽略自变量的取值范围而出错
例2.拖拉机刚开始工作时,油箱中有40L油,且工作时每小时耗油5L.
(1)写出拖拉机油箱中的余油量Q(单位:L)关于工作时间t(单位:h)的函数解析式;
(2)求出自变量t的取值范围;
(3)画出这个函数的图象.
易错点三 忽略一次函数 y=kx+b 中k≠0 的条件而出错
例3 当m 为何值时,函数是一次函数?
正解:由题意得m -3=1且m-2≠0,
解得m=±2且m≠2,所以m=-2.
易错点四 忽略正比例函数是特殊的一次函数而出错
例4.已知一次函数y=2x+m的图象不经过第二象限,求m的取值范围.
正解:当图象经过原点及第一、第三象限时,
m=0;当图象经过第一、三、四象限时,
m<0.综上可知m≤0.
易错点五 求直线与坐标轴围成的面积时漏解
例5.已知直线:y=kx+b(k≠0)过点(3,0),且与两坐标轴围成的三角形面积为3,求b的值.
1.(2023秋·邗江区期末)一次函数y1=ax+b与正比例函数y2=-bx在同一坐标系中的图象大致是( ____ )
A.___ B.___
C.___
C
D.___
押题预测
【解析】解:A、若a>0,b>0,则y=ax+b经过一、二、三象限,y=-bx经过二、四象限,
B、a>0,b<0,则y=ax+b经过一、三、四象限,y=-bx经过一、三象限,
C、若a>0,b>0,则y=ax+b经过一、二、三象限,y=-bx经过二、四象限,
D、若a<0,b<0,则y=ax+b经过二、三、四象限,y=-bx经过一、三象限,
故选:C.
2.(2023春·临汾期末)硫酸钠(Na2SO4)是一种主要的日用化工原料,主要用于制造洗涤剂和牛皮纸制浆工艺.硫酸钠的溶解度y(g)与温度t(℃)之间的对应关系如图所示,则下列说法正确的是( ____ )
A.当温度为60℃时,硫酸钠的溶解度为50g
B.硫酸钠的溶解度随着温度的升高而增大
C.当温度为40℃时,硫酸钠的溶解度最大
D.要使硫酸钠的溶解度大于43.7g,温度只能控制在40℃~80℃
C
【解析】解:由图象可知:
当温度为60℃时,碳酸钠的溶解度小于48.8g,故选项A说法错误,不符合题意;
0℃至40℃时,碳酸钠的溶解度随着温度的升高而增大,40℃至80℃时,碳酸钠的溶解度随着温度的升高而减小,故选项B说法错误,不符合题意;
当温度为40℃时,碳酸钠的溶解度最大,说法正确,故选项C符合题意;
要使碳酸钠的溶解度大于43.7g,温度可控制在接近40℃至80℃,故选项D说法错误,不符合题意.
故选:C.
3.(2023春·石景山区期末)已知点A(-2,y1),B(3,y2)在一次函数y=2x-3的图象上,则y1 ____ y2(填“>”,“<”或“=”).
【解析】解:∵k=2>0,
∴y随x的增大而增大.
又∵点A(-2,y1),B(3,y2)在一次函数y=2x-3的图象上,且-2<3,
∴y1<y2.
故答案为:<.
<
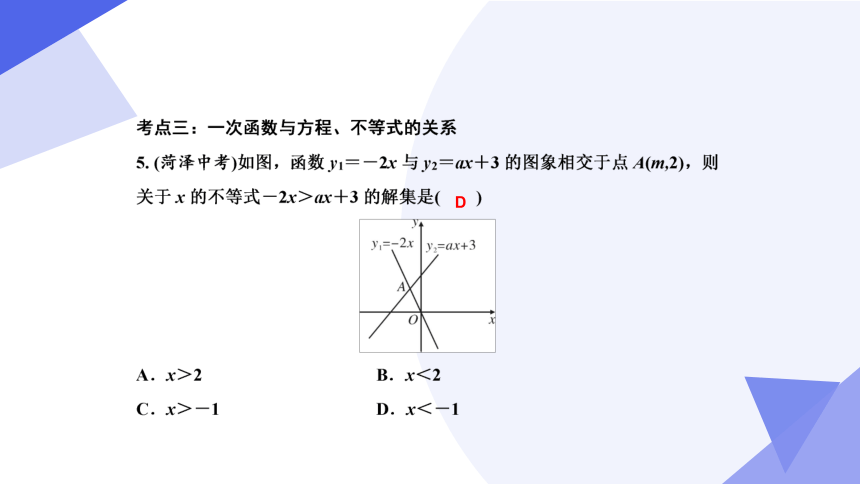
4.(2023春·微山县期末)根据图象,可得关于x的不等式kx>-x+3的解集是 _____ .
【解析】解:根据图象可知:两函数图象的交点为(1,2),
所以关于x的一元一次不等式kx>-x+3的解集为x>1,
故答案为:x>1.
x>1
5.(2023春·栾城区校级期末)如图,在平面直角坐标系中,直线l1,y=-x+5与x轴、y轴分别交于点A、B,直线l2,y=mx-m+4(m≠-1)与x轴、y轴分别交于点C、D,点P(2,n)在直线l2上.
_______
【解析】解:(1)∵y=mx-m+4=m(x-1)+4(m≠0),
∴当x=1时,y=4,
∴直线y=mx-m+4过定点M(1,4),
故答案为:过;
(2)在y=-x+5中,令x=0,则y=5,∴B(0,5),
∵点B、O关于点D对称,∴ ,
将点D的坐标代入y=mx-m+4,得 ,解得 ,
∴直线l2的解析式: ;
(2)若点B、O关于点D对称,求此时直线l2的解析式;
(1)直线y=mx-m+4过定点M(1,4)吗? ____ (填“过”或“不过”).
过
(3)在y=-x+5中,令y=0,则x=5,∴A(5,0),OA=5,
∵B(0,5),∴OB=5,∴ ,
∵直线y=mx-m+4过定点M(1,4),直线y=-x+5过点M(1,4),
∴两直线的交点为M(1,4),点M到y轴的距离为1,到x轴的距离为4,
①当 时, ,解得BD=5.
∵OB=5,∴D(0,0),∴-m+4=0,解得m=4;
②当 时, ,解得 ,
∵ ,∴ ,∴ ,∴ ,
解得 ,综上,m的值为4或 ;
(3)若直线l2将△AOB的面积分为1:4两部分,请求出m的值;
(4)当m=1时,直线l2的解析式为y=x+3,
∵将点P(2,5)向右平移2.5个单位得到点N,∴PN=2.5,
△AOB内部(不包括边界)的整点有:(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),
在y=x+3中,当y=1时,x=-2,
∵1+2=3>2.5,2+2=4>2.5,3+2=5>2.5,
∴当线段PN沿直线y=x+3向下平移时,线段PN不扫过△AOB内部(不包括边界)的整点:
(1,1),(2,1),(3,1);
在y=x+3中,当y=2时,x=-1,∵1+1=2<2.5,2+1=3>2.5,
∴当线段PN沿直线y=x+3向下平移时,线段PN扫过△AOB内部(不包括边界)的整点(1,2),不扫过(2,2),
在y=x+3中,当y=3时,x=0,∵1+0=1<2.5,
∴当线段PN沿直线y=x+3向下平移时,线段PN扫过△AOB内部(不包括边界)的整点(1,3),
综上,当线段PN沿直线y=x+3向下平移时,线段PN扫过△AOB内部(不包括边界)的整点有(1,2),(1,3).
(4)当m=1时,将点P(2,n)向右平移2.5个单位得到点N,当线段PN沿直线y=mx-m+4向下平移时,请直接写出线段PN扫过△AOB内部(不包括边界)的整点(横纵坐标都是整数的点)的坐标.
八年级人教版数学下册期末考点大串讲
串讲04 一次函数
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
五大易错易混经典例题+针对训练
5道期末真题对应考点练
四大重难点题型典例剖析+强化训练+三类期末重难点突破
四大常考点:知识梳理+考点分类训练
考点透视
知识梳理
C
考点分类训练
A
C
B
D
D
重难点题型典例剖析
B
D
A
C
强化训练
B
B
三、四
-4≤m≤4
200
B
期末重难点突破:一次函数
x>3
D
D
A
a≤3
易错易混
-1<x<2
针对训练
易错点一 不能正确理解函数的概念而出错
例1.[萍乡期末]下列关系式中,y不是x的函数的是( )
正解:在|y|=x中,x取一个非零的值,有两个y值与其对应,所以y不是x的函数.故选D.
D
易错点二 画函数图象时,忽略自变量的取值范围而出错
例2.拖拉机刚开始工作时,油箱中有40L油,且工作时每小时耗油5L.
(1)写出拖拉机油箱中的余油量Q(单位:L)关于工作时间t(单位:h)的函数解析式;
(2)求出自变量t的取值范围;
(3)画出这个函数的图象.
解:
(1)由题意可知Q=40-5t.
(2)因为油箱中有40L油,且工作时每小时耗油5L,
所以,
则自变量t的取值范围是.
正解:(3)当t=0 时,Q=40;
当t=8 时,Q=0.在平面直角坐标系中找到两点,
作线段即可,如图所示.
易错点二 画函数图象时,忽略自变量的取值范围而出错
例2.拖拉机刚开始工作时,油箱中有40L油,且工作时每小时耗油5L.
(1)写出拖拉机油箱中的余油量Q(单位:L)关于工作时间t(单位:h)的函数解析式;
(2)求出自变量t的取值范围;
(3)画出这个函数的图象.
易错点三 忽略一次函数 y=kx+b 中k≠0 的条件而出错
例3 当m 为何值时,函数是一次函数?
正解:由题意得m -3=1且m-2≠0,
解得m=±2且m≠2,所以m=-2.
易错点四 忽略正比例函数是特殊的一次函数而出错
例4.已知一次函数y=2x+m的图象不经过第二象限,求m的取值范围.
正解:当图象经过原点及第一、第三象限时,
m=0;当图象经过第一、三、四象限时,
m<0.综上可知m≤0.
易错点五 求直线与坐标轴围成的面积时漏解
例5.已知直线:y=kx+b(k≠0)过点(3,0),且与两坐标轴围成的三角形面积为3,求b的值.
1.(2023秋·邗江区期末)一次函数y1=ax+b与正比例函数y2=-bx在同一坐标系中的图象大致是( ____ )
A.___ B.___
C.___
C
D.___
押题预测
【解析】解:A、若a>0,b>0,则y=ax+b经过一、二、三象限,y=-bx经过二、四象限,
B、a>0,b<0,则y=ax+b经过一、三、四象限,y=-bx经过一、三象限,
C、若a>0,b>0,则y=ax+b经过一、二、三象限,y=-bx经过二、四象限,
D、若a<0,b<0,则y=ax+b经过二、三、四象限,y=-bx经过一、三象限,
故选:C.
2.(2023春·临汾期末)硫酸钠(Na2SO4)是一种主要的日用化工原料,主要用于制造洗涤剂和牛皮纸制浆工艺.硫酸钠的溶解度y(g)与温度t(℃)之间的对应关系如图所示,则下列说法正确的是( ____ )
A.当温度为60℃时,硫酸钠的溶解度为50g
B.硫酸钠的溶解度随着温度的升高而增大
C.当温度为40℃时,硫酸钠的溶解度最大
D.要使硫酸钠的溶解度大于43.7g,温度只能控制在40℃~80℃
C
【解析】解:由图象可知:
当温度为60℃时,碳酸钠的溶解度小于48.8g,故选项A说法错误,不符合题意;
0℃至40℃时,碳酸钠的溶解度随着温度的升高而增大,40℃至80℃时,碳酸钠的溶解度随着温度的升高而减小,故选项B说法错误,不符合题意;
当温度为40℃时,碳酸钠的溶解度最大,说法正确,故选项C符合题意;
要使碳酸钠的溶解度大于43.7g,温度可控制在接近40℃至80℃,故选项D说法错误,不符合题意.
故选:C.
3.(2023春·石景山区期末)已知点A(-2,y1),B(3,y2)在一次函数y=2x-3的图象上,则y1 ____ y2(填“>”,“<”或“=”).
【解析】解:∵k=2>0,
∴y随x的增大而增大.
又∵点A(-2,y1),B(3,y2)在一次函数y=2x-3的图象上,且-2<3,
∴y1<y2.
故答案为:<.
<
4.(2023春·微山县期末)根据图象,可得关于x的不等式kx>-x+3的解集是 _____ .
【解析】解:根据图象可知:两函数图象的交点为(1,2),
所以关于x的一元一次不等式kx>-x+3的解集为x>1,
故答案为:x>1.
x>1
5.(2023春·栾城区校级期末)如图,在平面直角坐标系中,直线l1,y=-x+5与x轴、y轴分别交于点A、B,直线l2,y=mx-m+4(m≠-1)与x轴、y轴分别交于点C、D,点P(2,n)在直线l2上.
_______
【解析】解:(1)∵y=mx-m+4=m(x-1)+4(m≠0),
∴当x=1时,y=4,
∴直线y=mx-m+4过定点M(1,4),
故答案为:过;
(2)在y=-x+5中,令x=0,则y=5,∴B(0,5),
∵点B、O关于点D对称,∴ ,
将点D的坐标代入y=mx-m+4,得 ,解得 ,
∴直线l2的解析式: ;
(2)若点B、O关于点D对称,求此时直线l2的解析式;
(1)直线y=mx-m+4过定点M(1,4)吗? ____ (填“过”或“不过”).
过
(3)在y=-x+5中,令y=0,则x=5,∴A(5,0),OA=5,
∵B(0,5),∴OB=5,∴ ,
∵直线y=mx-m+4过定点M(1,4),直线y=-x+5过点M(1,4),
∴两直线的交点为M(1,4),点M到y轴的距离为1,到x轴的距离为4,
①当 时, ,解得BD=5.
∵OB=5,∴D(0,0),∴-m+4=0,解得m=4;
②当 时, ,解得 ,
∵ ,∴ ,∴ ,∴ ,
解得 ,综上,m的值为4或 ;
(3)若直线l2将△AOB的面积分为1:4两部分,请求出m的值;
(4)当m=1时,直线l2的解析式为y=x+3,
∵将点P(2,5)向右平移2.5个单位得到点N,∴PN=2.5,
△AOB内部(不包括边界)的整点有:(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),
在y=x+3中,当y=1时,x=-2,
∵1+2=3>2.5,2+2=4>2.5,3+2=5>2.5,
∴当线段PN沿直线y=x+3向下平移时,线段PN不扫过△AOB内部(不包括边界)的整点:
(1,1),(2,1),(3,1);
在y=x+3中,当y=2时,x=-1,∵1+1=2<2.5,2+1=3>2.5,
∴当线段PN沿直线y=x+3向下平移时,线段PN扫过△AOB内部(不包括边界)的整点(1,2),不扫过(2,2),
在y=x+3中,当y=3时,x=0,∵1+0=1<2.5,
∴当线段PN沿直线y=x+3向下平移时,线段PN扫过△AOB内部(不包括边界)的整点(1,3),
综上,当线段PN沿直线y=x+3向下平移时,线段PN扫过△AOB内部(不包括边界)的整点有(1,2),(1,3).
(4)当m=1时,将点P(2,n)向右平移2.5个单位得到点N,当线段PN沿直线y=mx-m+4向下平移时,请直接写出线段PN扫过△AOB内部(不包括边界)的整点(横纵坐标都是整数的点)的坐标.
同课章节目录
