人教版八年级数学下学期题型模型培优专题练 06勾股定理最短路径问题(含解析)
文档属性
| 名称 | 人教版八年级数学下学期题型模型培优专题练 06勾股定理最短路径问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 17:11:54 | ||
图片预览


文档简介
培优专题06 利用勾股定理求最短路径问题
【考法导图】
解题技巧:
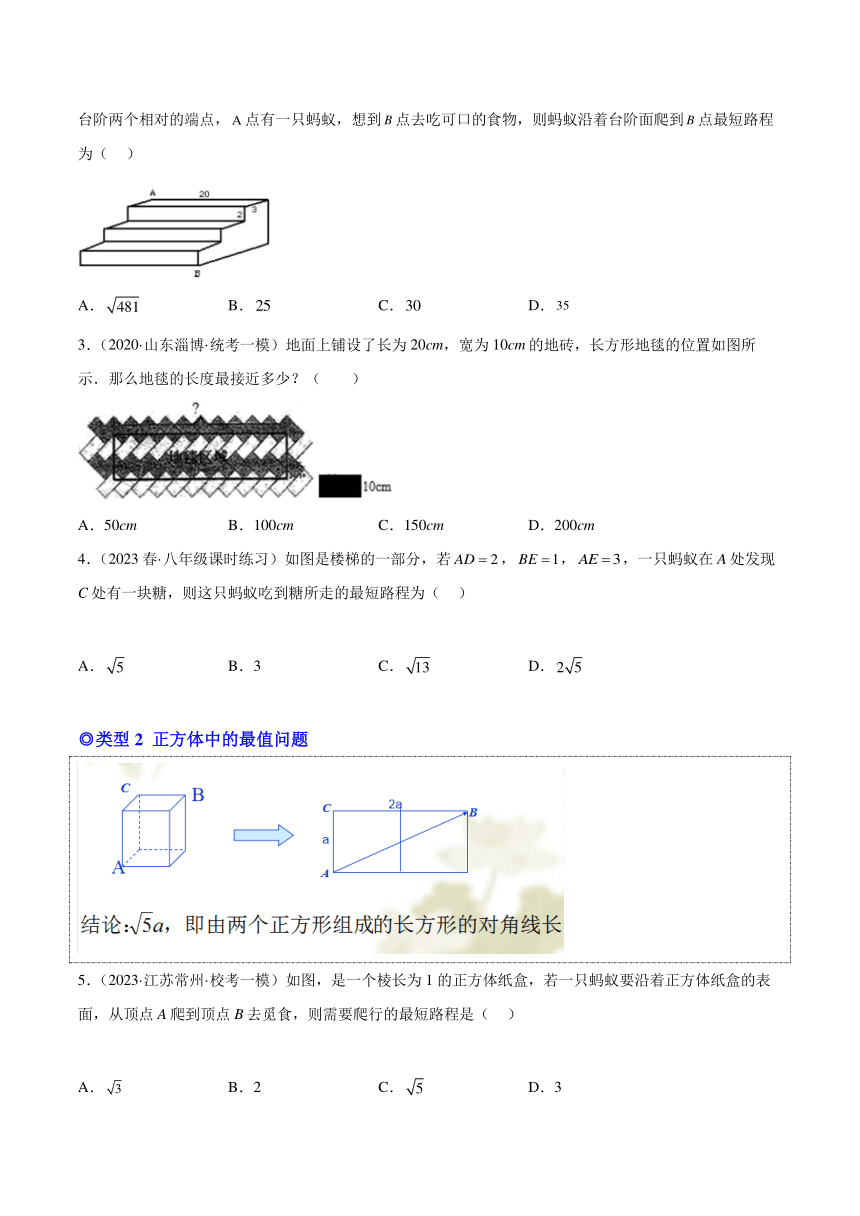
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
◎类型1 台阶中的最值问题
1.(2017秋·山东济南·八年级济南外国语学校校考期中)如图,是一个三级台阶,它的每一级的长,宽和高分别等于,和,和是这个台阶的两个相对的端点,点上有一只蚂蚁,想到点去吃可口的食物,请你想一想,这只蚂蚁从点出发,沿着台阶面爬到点,最短线路是( )
A. B. C. D.
2.(2023·全国·九年级专题练习)一个三级台阶,它的每一级的长宽和高分别为、、,和是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点最短路程为( )
A. B. C. D.
3.(2020·山东淄博·统考一模)地面上铺设了长为20cm,宽为10cm的地砖,长方形地毯的位置如图所示.那么地毯的长度最接近多少?( )
A.50cm B.100cm C.150cm D.200cm
4.(2023春·八年级课时练习)如图是楼梯的一部分,若,,,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )
A. B.3 C. D.
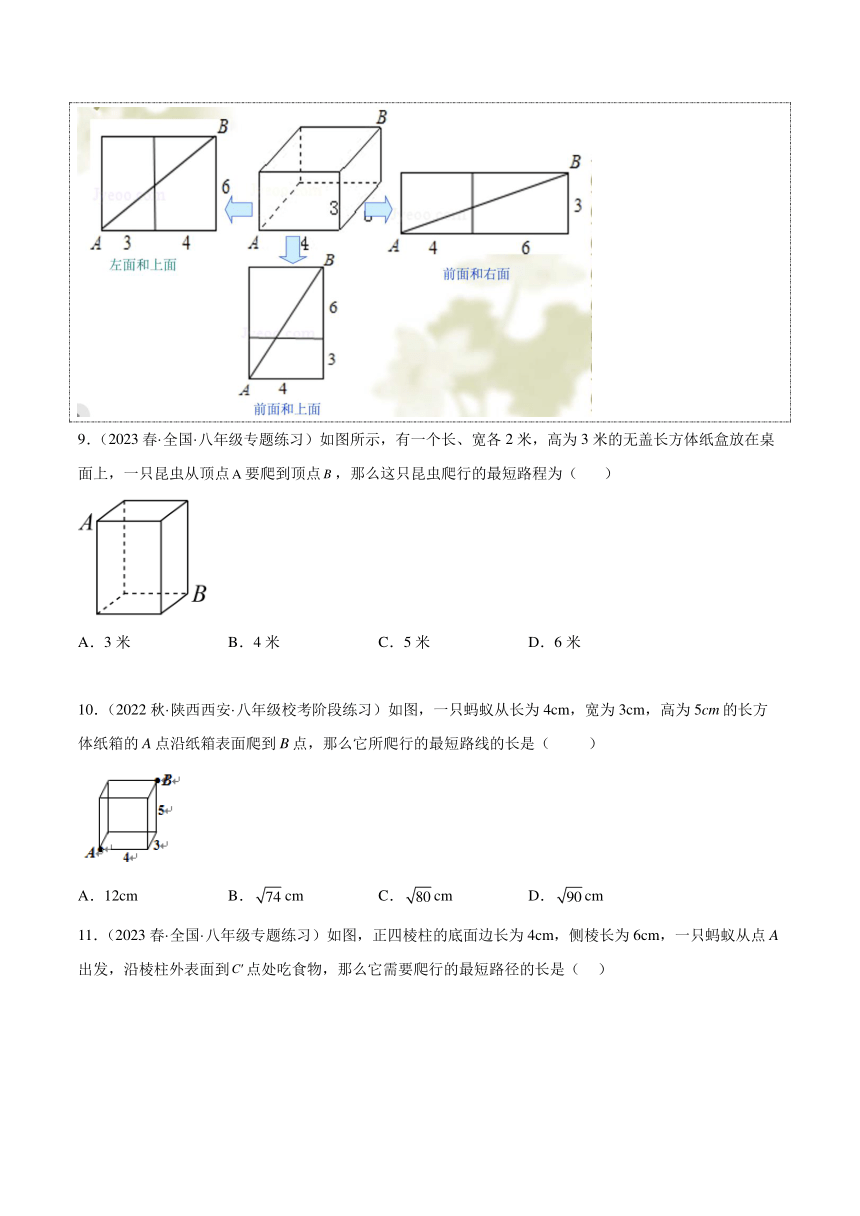
◎类型2 正方体中的最值问题
5.(2023·江苏常州·校考一模)如图,是一个棱长为1的正方体纸盒,若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是( )
A. B.2 C. D.3
6.(2023秋·陕西西安·八年级统考期末)如图,正方体盒子的棱长为2,M为的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为( )
A. B. C. D.
7.(2022秋·广东佛山·八年级校考阶段练习)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A. B. C. D.
8.(2023春·北京大兴·八年级北京市第八中学大兴分校校考阶段练习)如图,正方体盒子的棱长为2,M为BC的中点,则一只蚂蚁从A点沿盒子的表面爬行到M点的最短距离为( )
A. B.
C. D.
◎类型3 长方体中的最值问题
9.(2023春·全国·八年级专题练习)如图所示,有一个长、宽各2米,高为3米的无盖长方体纸盒放在桌面上,一只昆虫从顶点要爬到顶点,那么这只昆虫爬行的最短路程为( )
A.3米 B.4米 C.5米 D.6米
10.(2022秋·陕西西安·八年级校考阶段练习)如图,一只蚂蚁从长为4cm,宽为3cm,高为5cm的长方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )
A.12cm B.cm C.cm D.cm
11.(2023春·全国·八年级专题练习)如图,正四棱柱的底面边长为4cm,侧棱长为6cm,一只蚂蚁从点A出发,沿棱柱外表面到点处吃食物,那么它需要爬行的最短路径的长是( )
A. B.14cm C. D.10cm
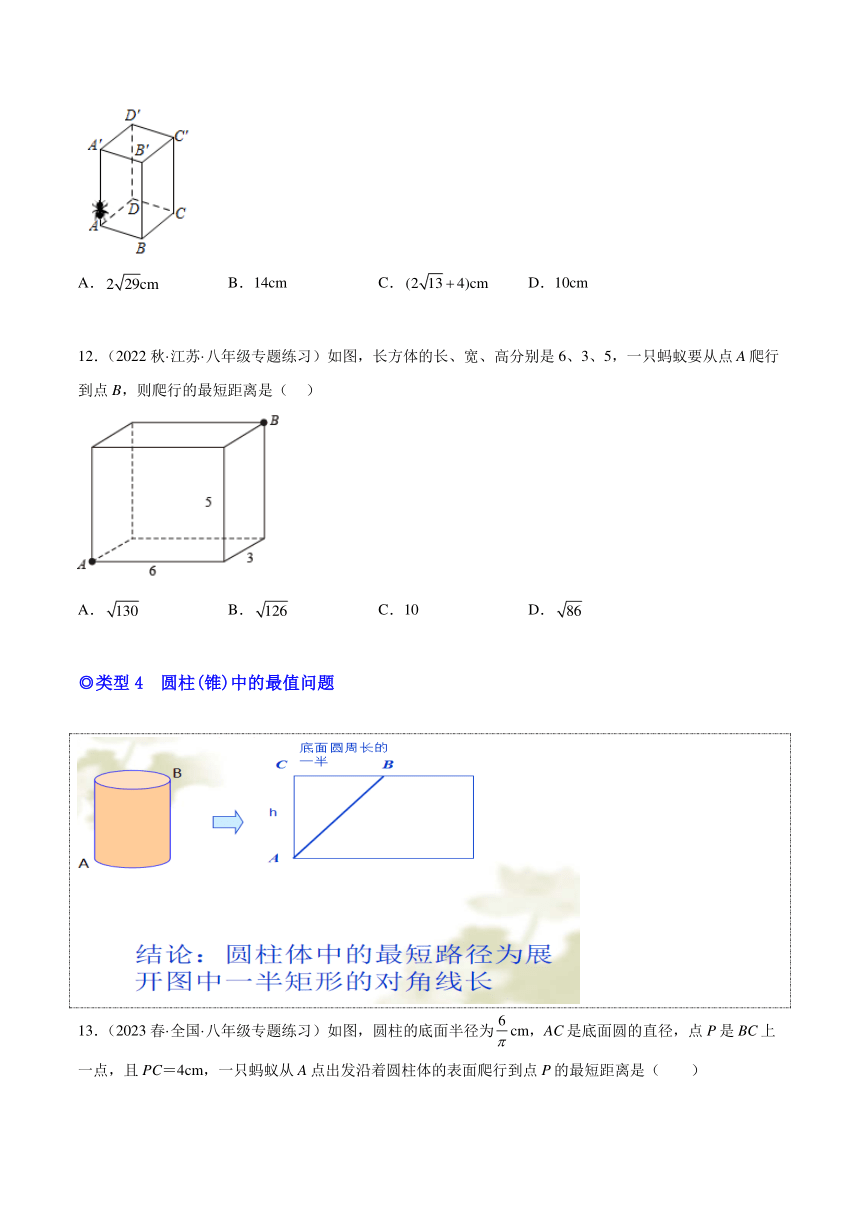
12.(2022秋·江苏·八年级专题练习)如图,长方体的长、宽、高分别是6、3、5,一只蚂蚁要从点A爬行到点B,则爬行的最短距离是( )
A. B. C.10 D.
◎类型4 圆柱(锥)中的最值问题
13.(2023春·全国·八年级专题练习)如图,圆柱的底面半径为cm,AC是底面圆的直径,点P是BC上一点,且PC=4cm,一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A.4cm B.2cm C.5cm D.10cm
14.(2022春·全国·八年级假期作业)如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.
A.15 B.20 C.18 D.30
15.(2022秋·全国·八年级专题练习)如图,有一个圆柱形玻璃杯,高为10cm,底而周长为12cm,在圆柱的下底面的内壁A处有一只蚂蚁,它想吃到在杯内离杯上沿2cm的点E处的一滴蜂蜜,求蚂蚁到达蜂蜜的最短距离( )
A.2cm B.2cm C.4cm D.10cm
16.(2019·全国·八年级专题练习)如图,一个圆柱形油罐,油罐的底面周长12m,高5m,要从点A环绕油罐建梯子,正好到达点A的正上方的点B,则梯子最短需要( )
A.12m B.13m C.17m D.20m
培优专题06 利用勾股定理求最短路径问题
【考法导图】
解题技巧:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
◎类型1 台阶中的最值问题
1.(2017秋·山东济南·八年级济南外国语学校校考期中)如图,是一个三级台阶,它的每一级的长,宽和高分别等于,和,和是这个台阶的两个相对的端点,点上有一只蚂蚁,想到点去吃可口的食物,请你想一想,这只蚂蚁从点出发,沿着台阶面爬到点,最短线路是( )
A. B. C. D.
【答案】B
【分析】将台阶展开,根据勾股定理即可求解.
【详解】将台阶展开,如下图,
因为AC=3×3+1×3=12,BC=5,
所以 =169,
所以AB=13(cm),
所以蚂蚁爬行的最短线路为13cm.
故选B.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.
2.(2023·全国·九年级专题练习)一个三级台阶,它的每一级的长宽和高分别为、、,和是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点最短路程为( )
A. B. C. D.
【答案】B
【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.
【详解】如图所示,
∵三级台阶平面展开图为长方形,长为20,宽为(2+3)×3,
∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.
由勾股定理得:=+=,
解得:.
故选:B.
【点睛】本题考查了平面展开-最短路径问题以及勾股定理的应用,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.
3.(2020·山东淄博·统考一模)地面上铺设了长为20cm,宽为10cm的地砖,长方形地毯的位置如图所示.那么地毯的长度最接近多少?( )
A.50cm B.100cm C.150cm D.200cm
【答案】C
【分析】根据等腰直角三角形的性质即可得到结论.
【详解】解:观察图像可知,地毯长可以看做是10个等腰直角三角形的斜边长度之和,
则斜边=,
∴长方形地毯的长为:10×10=100≈141.4cm,
故选C.
【点睛】本题考查了生活中的平移现象,等腰直角三角形的性质,正确的识别图形是解题的关键.
4.(2023春·八年级课时练习)如图是楼梯的一部分,若,,,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )
A. B.3 C. D.
【答案】D
【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从A点到C点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.
【详解】解:将台阶展开,如图,
因为DC=AE+BE=3+1=4,AD=2,
所以AC2=DC2+AD2=20,
所以AC=,
故选:D.
【点睛】本题考查了平面展开-最短路径问题,用到台阶的平面展开图,根据题意判断出长方形的长和宽是解题的关键.
◎类型2 正方体中的最值问题
5.(2023·江苏常州·校考一模)如图,是一个棱长为1的正方体纸盒,若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是( )
A. B.2 C. D.3
【答案】C
【分析】根据正方体展开图的特点,将正方体展开,然后利用勾股定理求解即可.
【详解】解:如图所示,将正方体展开,则,,
∴由勾股定理得,
∴需要爬行的最短路程是,
故选C.
【点睛】本题主要考查了勾股定理的实际应用,正确将正方体展开,利用勾股定理进行求解是解题的关键.
6.(2023秋·陕西西安·八年级统考期末)如图,正方体盒子的棱长为2,M为的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为( )
A. B. C. D.
【答案】C
【详解】先把图中展开,根据两点间线段距离最短,再根据勾股定理求出的长即可;
【解答】解:如图,连接,则线段的长就是蚂蚁需爬行的最短路程,
∵正方体的棱长为2,M是的中点,
∴,,,
由勾股定理得,
故选:C.
【点睛】本题考查两点间线段距离最短及勾股定理,解题的关键是理解最短路线.
7.(2022秋·广东佛山·八年级校考阶段练习)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A. B. C. D.
【答案】C
【分析】正方体侧面展开为长方形,确定蚂蚁的起点和终点,根据两点之间线段最短,根据勾股定理可求出路径长,
【详解】解:如图,
它运动的最短路程(cm),
故选:C.
【点睛】本题考查平面展开最短路径问题,掌握两点之间线段最短,找到起点终点,根据勾股定理求出是解题的关键.
8.(2023春·北京大兴·八年级北京市第八中学大兴分校校考阶段练习)如图,正方体盒子的棱长为2,M为BC的中点,则一只蚂蚁从A点沿盒子的表面爬行到M点的最短距离为( )
A. B.
C. D.
【答案】B
【分析】先利用展开图确定最短路线,再利用勾股定理求解即可.
【详解】解:如图,蚂蚁沿路线AM爬行时距离最短;
∵正方体盒子棱长为2,M为BC的中点,
∴,
∴,
故选:B.
【点睛】本题考查了蚂蚁爬行的最短路径为题,涉及到了正方形的性质、正方体的展开图、勾股定理、两点之间线段最短等知识,解题关键是牢记相关概念与灵活应用.
◎类型3 长方体中的最值问题
9.(2023春·全国·八年级专题练习)如图所示,有一个长、宽各2米,高为3米的无盖长方体纸盒放在桌面上,一只昆虫从顶点要爬到顶点,那么这只昆虫爬行的最短路程为( )
A.3米 B.4米 C.5米 D.6米
【答案】C
【分析】分别画出三个路径的示意图,利用勾股定理求出路程,再从中找出最短路程即可.
【详解】解:由题意,有以下三个路径:
①如图,路径一:
则这只昆虫爬行的路程为(米);
②如图,路径二:
则这只昆虫爬行的路程为(米);
③如图,路径三:
则这只昆虫爬行的路程为(米);
因为,
所以这只昆虫爬行的最短路程为5米,
故选:C.
【点睛】本题考查了勾股定理的应用,正确画出三个路径的示意图是解题关键.
10.(2022秋·陕西西安·八年级校考阶段练习)如图,一只蚂蚁从长为4cm,宽为3cm,高为5cm的长方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )
A.12cm B.cm C.cm D.cm
【答案】B
【分析】先将图形展开,再根据两点之间线段最短,再由勾股定理求解即可.
【详解】解:将长方体展开,如图1所示,连接A、B,根据两点之间线段最短,AB= cm;
如图2所示,cm,
如图3所示,cm,
∵<4<,
∴蚂蚁所行的最短路线为cm.
【点睛】本题考查最短路径问题,将长方体展开,根据两点之间线段最短,运用勾股定理是解题.
11.(2023春·全国·八年级专题练习)如图,正四棱柱的底面边长为4cm,侧棱长为6cm,一只蚂蚁从点A出发,沿棱柱外表面到点处吃食物,那么它需要爬行的最短路径的长是( )
A. B.14cm C. D.10cm
【答案】D
【分析】把正四棱柱展开为平面图形,分两种情形求出路径,比较即可解答.
【详解】解:把正四棱柱展开为平面图形,分两种情形:
如图1中,,
如图2中,,
∵ ,
∴爬行的最短路径是10cm.
故选:D
【点睛】本题考查平面展开-最短路径问题,涉及了勾股定理的应用,解题的关键是将问题进行转化,然后根据勾股定理求解.
12.(2022秋·江苏·八年级专题练习)如图,长方体的长、宽、高分别是6、3、5,一只蚂蚁要从点A爬行到点B,则爬行的最短距离是( )
A. B. C.10 D.
【答案】C
【分析】做此题要把这个长方体中蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.
【详解】解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是8和6,
则所走的最短线段是=10;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是11和3,
所以走的最短线段是;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是9和5,
所以走的最短线段是;
∵10<<,
三种情况比较而言,第一种情况最短,最短路程=10,
故选:C.
【点睛】本题考查了平面展开---最短路径问题,解题的关键是将图形展开,转化为直角三角形利用勾股定理解答.
◎类型4 圆柱(锥)中的最值问题
13.(2023春·全国·八年级专题练习)如图,圆柱的底面半径为cm,AC是底面圆的直径,点P是BC上一点,且PC=4cm,一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A.4cm B.2cm C.5cm D.10cm
【答案】B
【分析】把圆柱侧面展开后,连接AP.由已知可求得圆柱底面圆的周长,从而可求得周长的一半,由勾股定理即可计算出AP的长.
【详解】侧面展开图如图所示:
∵圆柱的底面半径为cm,
∴圆柱的底面周长为12cm,
∴AC′=6cm.
在Rt△ACP中,AP==2(cm).
故选:B.
【点睛】本题考查了勾股定理的应用,关键是把圆柱展开,即把空间问题转化为平面问题来解决,体现了转化思想.
14.(2022春·全国·八年级假期作业)如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.
A.15 B.20 C.18 D.30
【答案】A
【分析】把圆柱沿蚂蚁所在的高剪开并展开在一个平面内,得到一个矩形,作A点关于DF的对称点B,分别连接BD、BC,过点C作CE⊥DH于点E,则BC就是蚂蚁到达蜂蜜的最短距离,根据勾股定理即可求得BC的长.
【详解】把圆柱沿蚂蚁所在的高剪开并展开在一个平面内,得到一个矩形,作A点关于DF的对称点B,分别连接BD、BC,过点C作CE⊥DH于点E,如图所示:
则DB=AD=4cm,
由题意及辅助线作法知,M与N分别为GH与DF的中点,且四边形CMHE为长方形,
∴CE=MH=9cm,EH=CM=4cm,
∴DE=DH-EH=12-4=8cm,
∴BE=DE+DB=8+4=12cm ,
在Rt△BEC中,由勾股定理得:,
即蚂蚁到达蜂蜜的最短距离为 15cm,
故选;:A.
【点睛】本题考查了勾股定理,两点间线段最短,关键是把空间问题转化为平面问题解决,这是数学上一种重要的转化思想.
15.(2022秋·全国·八年级专题练习)如图,有一个圆柱形玻璃杯,高为10cm,底而周长为12cm,在圆柱的下底面的内壁A处有一只蚂蚁,它想吃到在杯内离杯上沿2cm的点E处的一滴蜂蜜,求蚂蚁到达蜂蜜的最短距离( )
A.2cm B.2cm C.4cm D.10cm
【答案】D
【分析】根据题意画出图形,然后根据勾股定理,即可求解.
【详解】解:如图,
根据题意得:BC=10cm,AB= cm,CE=2cm,
∴BE=BC-CE=8cm,
在 中,由勾股定理得:
,
即蚂蚁到达蜂蜜的最短距离10cm.
故选:D.
【点睛】本题主要考查了勾股定理的应用,明确题意,画出图形是解题的关键.
16.(2019·全国·八年级专题练习)如图,一个圆柱形油罐,油罐的底面周长12m,高5m,要从点A环绕油罐建梯子,正好到达点A的正上方的点B,则梯子最短需要( )
A.12m B.13m C.17m D.20m
【答案】B
【分析】先把圆柱的侧面展开得到一个长方形,利用勾股定理求出的长即可得到答案.
【详解】解:将圆柱形油罐的侧面展开如图所示,
由题意可知,在中,,
∴由勾股定理可得:,
∴梯子最短需要13m.
故选B.
【点睛】本题主要考查了勾股定理的应用,本题的解题要点是:将圆柱的侧面展开,结合题意就可将问题转化到中,这样就可利用“勾股定理”求出的长度,从而得到梯子的最短长度.
【考法导图】
解题技巧:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
◎类型1 台阶中的最值问题
1.(2017秋·山东济南·八年级济南外国语学校校考期中)如图,是一个三级台阶,它的每一级的长,宽和高分别等于,和,和是这个台阶的两个相对的端点,点上有一只蚂蚁,想到点去吃可口的食物,请你想一想,这只蚂蚁从点出发,沿着台阶面爬到点,最短线路是( )
A. B. C. D.
2.(2023·全国·九年级专题练习)一个三级台阶,它的每一级的长宽和高分别为、、,和是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点最短路程为( )
A. B. C. D.
3.(2020·山东淄博·统考一模)地面上铺设了长为20cm,宽为10cm的地砖,长方形地毯的位置如图所示.那么地毯的长度最接近多少?( )
A.50cm B.100cm C.150cm D.200cm
4.(2023春·八年级课时练习)如图是楼梯的一部分,若,,,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )
A. B.3 C. D.
◎类型2 正方体中的最值问题
5.(2023·江苏常州·校考一模)如图,是一个棱长为1的正方体纸盒,若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是( )
A. B.2 C. D.3
6.(2023秋·陕西西安·八年级统考期末)如图,正方体盒子的棱长为2,M为的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为( )
A. B. C. D.
7.(2022秋·广东佛山·八年级校考阶段练习)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A. B. C. D.
8.(2023春·北京大兴·八年级北京市第八中学大兴分校校考阶段练习)如图,正方体盒子的棱长为2,M为BC的中点,则一只蚂蚁从A点沿盒子的表面爬行到M点的最短距离为( )
A. B.
C. D.
◎类型3 长方体中的最值问题
9.(2023春·全国·八年级专题练习)如图所示,有一个长、宽各2米,高为3米的无盖长方体纸盒放在桌面上,一只昆虫从顶点要爬到顶点,那么这只昆虫爬行的最短路程为( )
A.3米 B.4米 C.5米 D.6米
10.(2022秋·陕西西安·八年级校考阶段练习)如图,一只蚂蚁从长为4cm,宽为3cm,高为5cm的长方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )
A.12cm B.cm C.cm D.cm
11.(2023春·全国·八年级专题练习)如图,正四棱柱的底面边长为4cm,侧棱长为6cm,一只蚂蚁从点A出发,沿棱柱外表面到点处吃食物,那么它需要爬行的最短路径的长是( )
A. B.14cm C. D.10cm
12.(2022秋·江苏·八年级专题练习)如图,长方体的长、宽、高分别是6、3、5,一只蚂蚁要从点A爬行到点B,则爬行的最短距离是( )
A. B. C.10 D.
◎类型4 圆柱(锥)中的最值问题
13.(2023春·全国·八年级专题练习)如图,圆柱的底面半径为cm,AC是底面圆的直径,点P是BC上一点,且PC=4cm,一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A.4cm B.2cm C.5cm D.10cm
14.(2022春·全国·八年级假期作业)如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.
A.15 B.20 C.18 D.30
15.(2022秋·全国·八年级专题练习)如图,有一个圆柱形玻璃杯,高为10cm,底而周长为12cm,在圆柱的下底面的内壁A处有一只蚂蚁,它想吃到在杯内离杯上沿2cm的点E处的一滴蜂蜜,求蚂蚁到达蜂蜜的最短距离( )
A.2cm B.2cm C.4cm D.10cm
16.(2019·全国·八年级专题练习)如图,一个圆柱形油罐,油罐的底面周长12m,高5m,要从点A环绕油罐建梯子,正好到达点A的正上方的点B,则梯子最短需要( )
A.12m B.13m C.17m D.20m
培优专题06 利用勾股定理求最短路径问题
【考法导图】
解题技巧:
把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
◎类型1 台阶中的最值问题
1.(2017秋·山东济南·八年级济南外国语学校校考期中)如图,是一个三级台阶,它的每一级的长,宽和高分别等于,和,和是这个台阶的两个相对的端点,点上有一只蚂蚁,想到点去吃可口的食物,请你想一想,这只蚂蚁从点出发,沿着台阶面爬到点,最短线路是( )
A. B. C. D.
【答案】B
【分析】将台阶展开,根据勾股定理即可求解.
【详解】将台阶展开,如下图,
因为AC=3×3+1×3=12,BC=5,
所以 =169,
所以AB=13(cm),
所以蚂蚁爬行的最短线路为13cm.
故选B.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.
2.(2023·全国·九年级专题练习)一个三级台阶,它的每一级的长宽和高分别为、、,和是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点最短路程为( )
A. B. C. D.
【答案】B
【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.
【详解】如图所示,
∵三级台阶平面展开图为长方形,长为20,宽为(2+3)×3,
∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.
由勾股定理得:=+=,
解得:.
故选:B.
【点睛】本题考查了平面展开-最短路径问题以及勾股定理的应用,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.
3.(2020·山东淄博·统考一模)地面上铺设了长为20cm,宽为10cm的地砖,长方形地毯的位置如图所示.那么地毯的长度最接近多少?( )
A.50cm B.100cm C.150cm D.200cm
【答案】C
【分析】根据等腰直角三角形的性质即可得到结论.
【详解】解:观察图像可知,地毯长可以看做是10个等腰直角三角形的斜边长度之和,
则斜边=,
∴长方形地毯的长为:10×10=100≈141.4cm,
故选C.
【点睛】本题考查了生活中的平移现象,等腰直角三角形的性质,正确的识别图形是解题的关键.
4.(2023春·八年级课时练习)如图是楼梯的一部分,若,,,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )
A. B.3 C. D.
【答案】D
【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从A点到C点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.
【详解】解:将台阶展开,如图,
因为DC=AE+BE=3+1=4,AD=2,
所以AC2=DC2+AD2=20,
所以AC=,
故选:D.
【点睛】本题考查了平面展开-最短路径问题,用到台阶的平面展开图,根据题意判断出长方形的长和宽是解题的关键.
◎类型2 正方体中的最值问题
5.(2023·江苏常州·校考一模)如图,是一个棱长为1的正方体纸盒,若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是( )
A. B.2 C. D.3
【答案】C
【分析】根据正方体展开图的特点,将正方体展开,然后利用勾股定理求解即可.
【详解】解:如图所示,将正方体展开,则,,
∴由勾股定理得,
∴需要爬行的最短路程是,
故选C.
【点睛】本题主要考查了勾股定理的实际应用,正确将正方体展开,利用勾股定理进行求解是解题的关键.
6.(2023秋·陕西西安·八年级统考期末)如图,正方体盒子的棱长为2,M为的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为( )
A. B. C. D.
【答案】C
【详解】先把图中展开,根据两点间线段距离最短,再根据勾股定理求出的长即可;
【解答】解:如图,连接,则线段的长就是蚂蚁需爬行的最短路程,
∵正方体的棱长为2,M是的中点,
∴,,,
由勾股定理得,
故选:C.
【点睛】本题考查两点间线段距离最短及勾股定理,解题的关键是理解最短路线.
7.(2022秋·广东佛山·八年级校考阶段练习)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A. B. C. D.
【答案】C
【分析】正方体侧面展开为长方形,确定蚂蚁的起点和终点,根据两点之间线段最短,根据勾股定理可求出路径长,
【详解】解:如图,
它运动的最短路程(cm),
故选:C.
【点睛】本题考查平面展开最短路径问题,掌握两点之间线段最短,找到起点终点,根据勾股定理求出是解题的关键.
8.(2023春·北京大兴·八年级北京市第八中学大兴分校校考阶段练习)如图,正方体盒子的棱长为2,M为BC的中点,则一只蚂蚁从A点沿盒子的表面爬行到M点的最短距离为( )
A. B.
C. D.
【答案】B
【分析】先利用展开图确定最短路线,再利用勾股定理求解即可.
【详解】解:如图,蚂蚁沿路线AM爬行时距离最短;
∵正方体盒子棱长为2,M为BC的中点,
∴,
∴,
故选:B.
【点睛】本题考查了蚂蚁爬行的最短路径为题,涉及到了正方形的性质、正方体的展开图、勾股定理、两点之间线段最短等知识,解题关键是牢记相关概念与灵活应用.
◎类型3 长方体中的最值问题
9.(2023春·全国·八年级专题练习)如图所示,有一个长、宽各2米,高为3米的无盖长方体纸盒放在桌面上,一只昆虫从顶点要爬到顶点,那么这只昆虫爬行的最短路程为( )
A.3米 B.4米 C.5米 D.6米
【答案】C
【分析】分别画出三个路径的示意图,利用勾股定理求出路程,再从中找出最短路程即可.
【详解】解:由题意,有以下三个路径:
①如图,路径一:
则这只昆虫爬行的路程为(米);
②如图,路径二:
则这只昆虫爬行的路程为(米);
③如图,路径三:
则这只昆虫爬行的路程为(米);
因为,
所以这只昆虫爬行的最短路程为5米,
故选:C.
【点睛】本题考查了勾股定理的应用,正确画出三个路径的示意图是解题关键.
10.(2022秋·陕西西安·八年级校考阶段练习)如图,一只蚂蚁从长为4cm,宽为3cm,高为5cm的长方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )
A.12cm B.cm C.cm D.cm
【答案】B
【分析】先将图形展开,再根据两点之间线段最短,再由勾股定理求解即可.
【详解】解:将长方体展开,如图1所示,连接A、B,根据两点之间线段最短,AB= cm;
如图2所示,cm,
如图3所示,cm,
∵<4<,
∴蚂蚁所行的最短路线为cm.
【点睛】本题考查最短路径问题,将长方体展开,根据两点之间线段最短,运用勾股定理是解题.
11.(2023春·全国·八年级专题练习)如图,正四棱柱的底面边长为4cm,侧棱长为6cm,一只蚂蚁从点A出发,沿棱柱外表面到点处吃食物,那么它需要爬行的最短路径的长是( )
A. B.14cm C. D.10cm
【答案】D
【分析】把正四棱柱展开为平面图形,分两种情形求出路径,比较即可解答.
【详解】解:把正四棱柱展开为平面图形,分两种情形:
如图1中,,
如图2中,,
∵ ,
∴爬行的最短路径是10cm.
故选:D
【点睛】本题考查平面展开-最短路径问题,涉及了勾股定理的应用,解题的关键是将问题进行转化,然后根据勾股定理求解.
12.(2022秋·江苏·八年级专题练习)如图,长方体的长、宽、高分别是6、3、5,一只蚂蚁要从点A爬行到点B,则爬行的最短距离是( )
A. B. C.10 D.
【答案】C
【分析】做此题要把这个长方体中蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.
【详解】解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是8和6,
则所走的最短线段是=10;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是11和3,
所以走的最短线段是;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是9和5,
所以走的最短线段是;
∵10<<,
三种情况比较而言,第一种情况最短,最短路程=10,
故选:C.
【点睛】本题考查了平面展开---最短路径问题,解题的关键是将图形展开,转化为直角三角形利用勾股定理解答.
◎类型4 圆柱(锥)中的最值问题
13.(2023春·全国·八年级专题练习)如图,圆柱的底面半径为cm,AC是底面圆的直径,点P是BC上一点,且PC=4cm,一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A.4cm B.2cm C.5cm D.10cm
【答案】B
【分析】把圆柱侧面展开后,连接AP.由已知可求得圆柱底面圆的周长,从而可求得周长的一半,由勾股定理即可计算出AP的长.
【详解】侧面展开图如图所示:
∵圆柱的底面半径为cm,
∴圆柱的底面周长为12cm,
∴AC′=6cm.
在Rt△ACP中,AP==2(cm).
故选:B.
【点睛】本题考查了勾股定理的应用,关键是把圆柱展开,即把空间问题转化为平面问题来解决,体现了转化思想.
14.(2022春·全国·八年级假期作业)如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.
A.15 B.20 C.18 D.30
【答案】A
【分析】把圆柱沿蚂蚁所在的高剪开并展开在一个平面内,得到一个矩形,作A点关于DF的对称点B,分别连接BD、BC,过点C作CE⊥DH于点E,则BC就是蚂蚁到达蜂蜜的最短距离,根据勾股定理即可求得BC的长.
【详解】把圆柱沿蚂蚁所在的高剪开并展开在一个平面内,得到一个矩形,作A点关于DF的对称点B,分别连接BD、BC,过点C作CE⊥DH于点E,如图所示:
则DB=AD=4cm,
由题意及辅助线作法知,M与N分别为GH与DF的中点,且四边形CMHE为长方形,
∴CE=MH=9cm,EH=CM=4cm,
∴DE=DH-EH=12-4=8cm,
∴BE=DE+DB=8+4=12cm ,
在Rt△BEC中,由勾股定理得:,
即蚂蚁到达蜂蜜的最短距离为 15cm,
故选;:A.
【点睛】本题考查了勾股定理,两点间线段最短,关键是把空间问题转化为平面问题解决,这是数学上一种重要的转化思想.
15.(2022秋·全国·八年级专题练习)如图,有一个圆柱形玻璃杯,高为10cm,底而周长为12cm,在圆柱的下底面的内壁A处有一只蚂蚁,它想吃到在杯内离杯上沿2cm的点E处的一滴蜂蜜,求蚂蚁到达蜂蜜的最短距离( )
A.2cm B.2cm C.4cm D.10cm
【答案】D
【分析】根据题意画出图形,然后根据勾股定理,即可求解.
【详解】解:如图,
根据题意得:BC=10cm,AB= cm,CE=2cm,
∴BE=BC-CE=8cm,
在 中,由勾股定理得:
,
即蚂蚁到达蜂蜜的最短距离10cm.
故选:D.
【点睛】本题主要考查了勾股定理的应用,明确题意,画出图形是解题的关键.
16.(2019·全国·八年级专题练习)如图,一个圆柱形油罐,油罐的底面周长12m,高5m,要从点A环绕油罐建梯子,正好到达点A的正上方的点B,则梯子最短需要( )
A.12m B.13m C.17m D.20m
【答案】B
【分析】先把圆柱的侧面展开得到一个长方形,利用勾股定理求出的长即可得到答案.
【详解】解:将圆柱形油罐的侧面展开如图所示,
由题意可知,在中,,
∴由勾股定理可得:,
∴梯子最短需要13m.
故选B.
【点睛】本题主要考查了勾股定理的应用,本题的解题要点是:将圆柱的侧面展开,结合题意就可将问题转化到中,这样就可利用“勾股定理”求出的长度,从而得到梯子的最短长度.
