九年级数学上册试题 25.3 解直角三角形 同步测试-沪教版(含解析)
文档属性
| 名称 | 九年级数学上册试题 25.3 解直角三角形 同步测试-沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 17:25:22 | ||
图片预览


文档简介
25.3解直角三角形
一、选择题.
1.已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么BC的长为( )
A.10cos50° B.10sin50° C.10tan50° D.10cot50°
2.在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,垂足为D,下列四个选项中,不正确的是( )
A. B. C. D.
3.在平面直角坐标系xOy中,已知点P(1,3),点P与原点O的连线与x轴的正半轴的夹角为α(0°<α<90°),那么tanα的值是( )
A. B. C. D.3
4.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A=α,那么CD的长为( )
A.m sinα tanα B.m sinα cosα
C.m cosα tanα D.m cosα cotα
5.在△ABC中,如果sinA,cotB,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
6.如图,直线OA过点(2,1),直线OA与x轴的夹角为α,则tanα的值为( )
A. B. C.2 D.
7.在Rt△ABC中,∠C=90°,如果BC=2,tanB=2,那么AC=( )
A.1 B.4 C. D.2
8.在Rt△ABC中,∠C=90°,如果AC=8,BC=6,那么∠B的余切值为( )
A. B. C. D.
9.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴的夹角α的余切值是( )
A. B. C. D.
10.如图,在等腰△ABC中,AB=AC,BD是AC边上的高,cosC,则△BCD与△ABD的面积比是( )
A.1:3 B.2:7 C.2:9 D.2:11
二、填空题
11.在△ABC中,AB:AC:BC=1:2:,那么tanB= .
12.在△ABC中,AB=5,BC=8,∠B=60°,则△ABC的面积是 .
13.如图,点P在线段BC上,AB⊥BC,DP⊥AP,CD⊥DP,如果BC=10,AB=2,tanC,那么DP的长是 .
14.在直角坐标平面内有一点A(12,5),点A与原点O的连线与x轴的正半轴的夹角为θ,那么cosθ= .
15.已知锐角△ABC中,AB=5,BC=7,sinB,那么∠C= 度.
16.如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE,ED=5,如果△ECD的面积是6,那么BC的长是 .
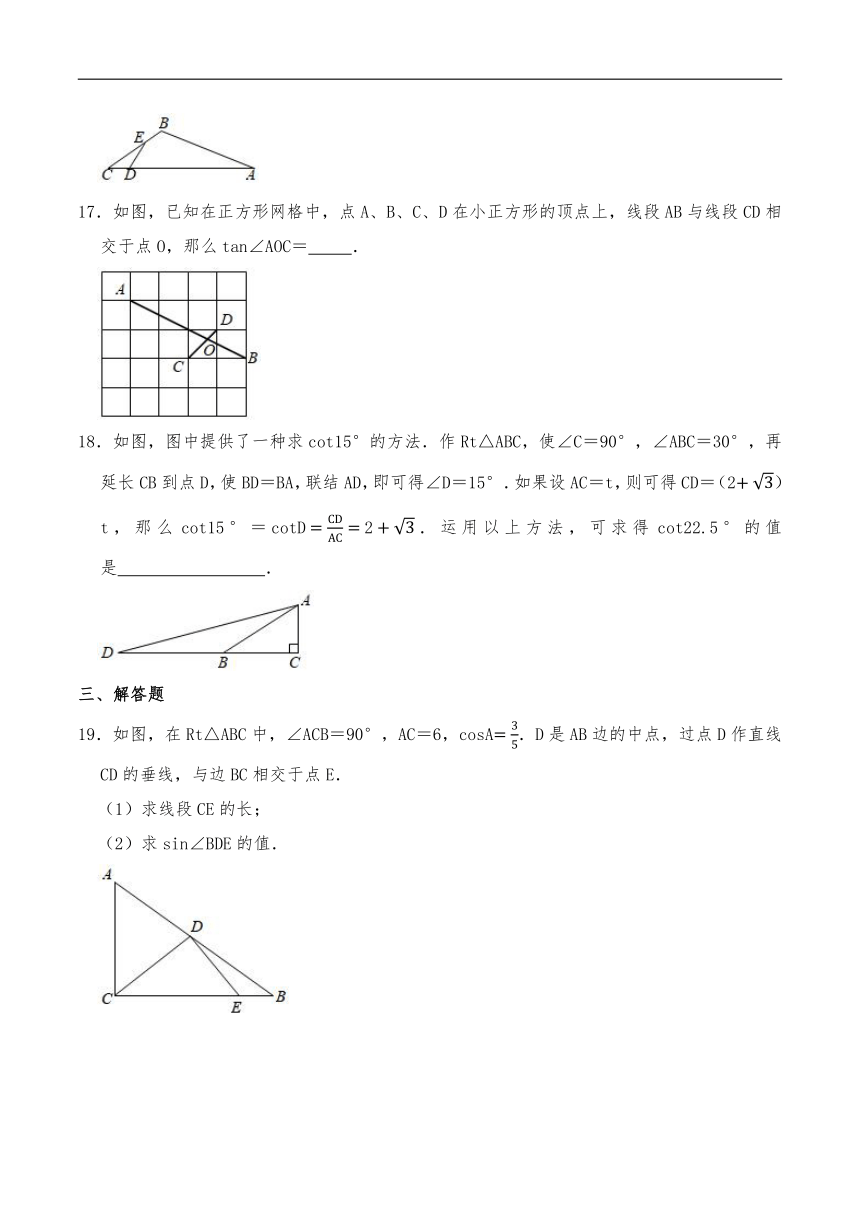
17.如图,已知在正方形网格中,点A、B、C、D在小正方形的顶点上,线段AB与线段CD相交于点O,那么tan∠AOC= .
18.如图,图中提供了一种求cot15°的方法.作Rt△ABC,使∠C=90°,∠ABC=30°,再延长CB到点D,使BD=BA,联结AD,即可得∠D=15°.如果设AC=t,则可得CD=(2)t,那么cot15°=cotD2.运用以上方法,可求得cot22.5°的值是 .
三、解答题
19.如图,在Rt△ABC中,∠ACB=90°,AC=6,cosA.D是AB边的中点,过点D作直线CD的垂线,与边BC相交于点E.
(1)求线段CE的长;
(2)求sin∠BDE的值.
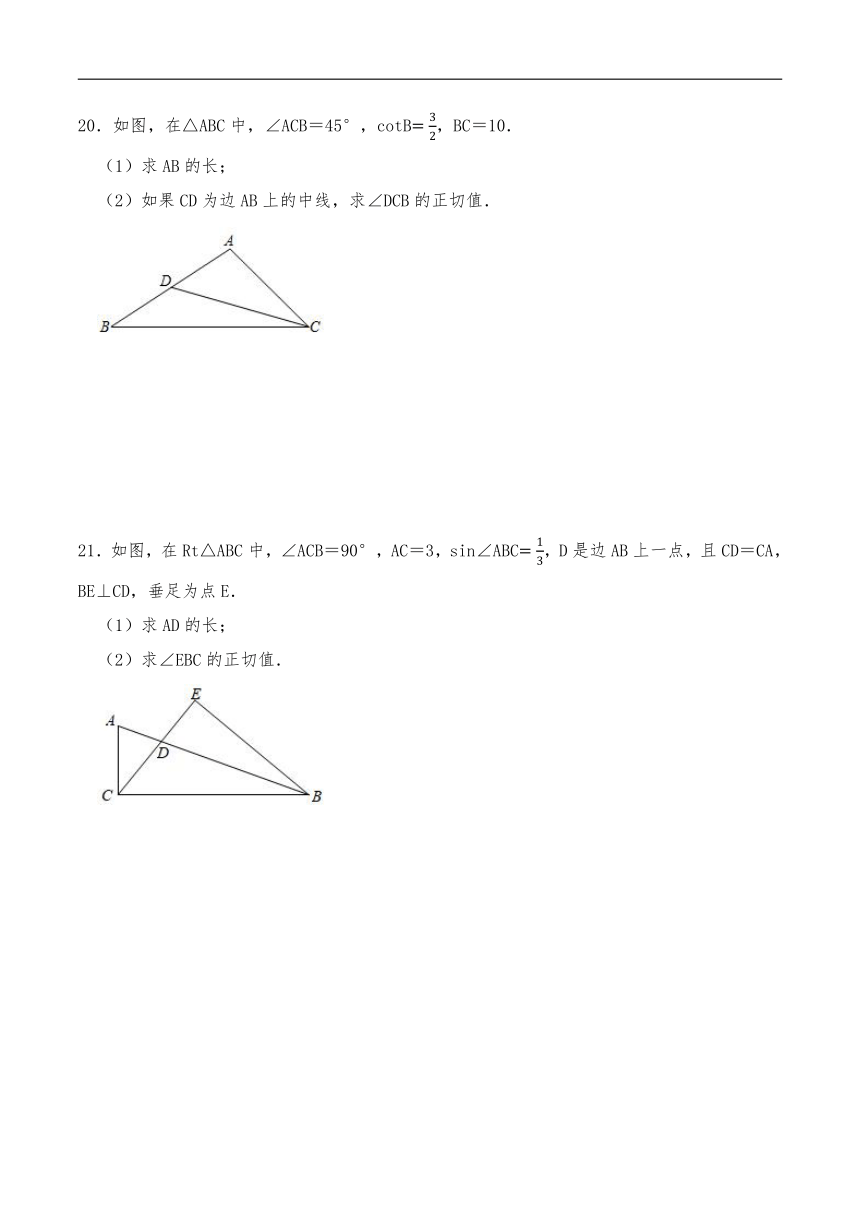
20.如图,在△ABC中,∠ACB=45°,cotB,BC=10.
(1)求AB的长;
(2)如果CD为边AB上的中线,求∠DCB的正切值.
21.如图,在Rt△ABC中,∠ACB=90°,AC=3,sin∠ABC,D是边AB上一点,且CD=CA,BE⊥CD,垂足为点E.
(1)求AD的长;
(2)求∠EBC的正切值.
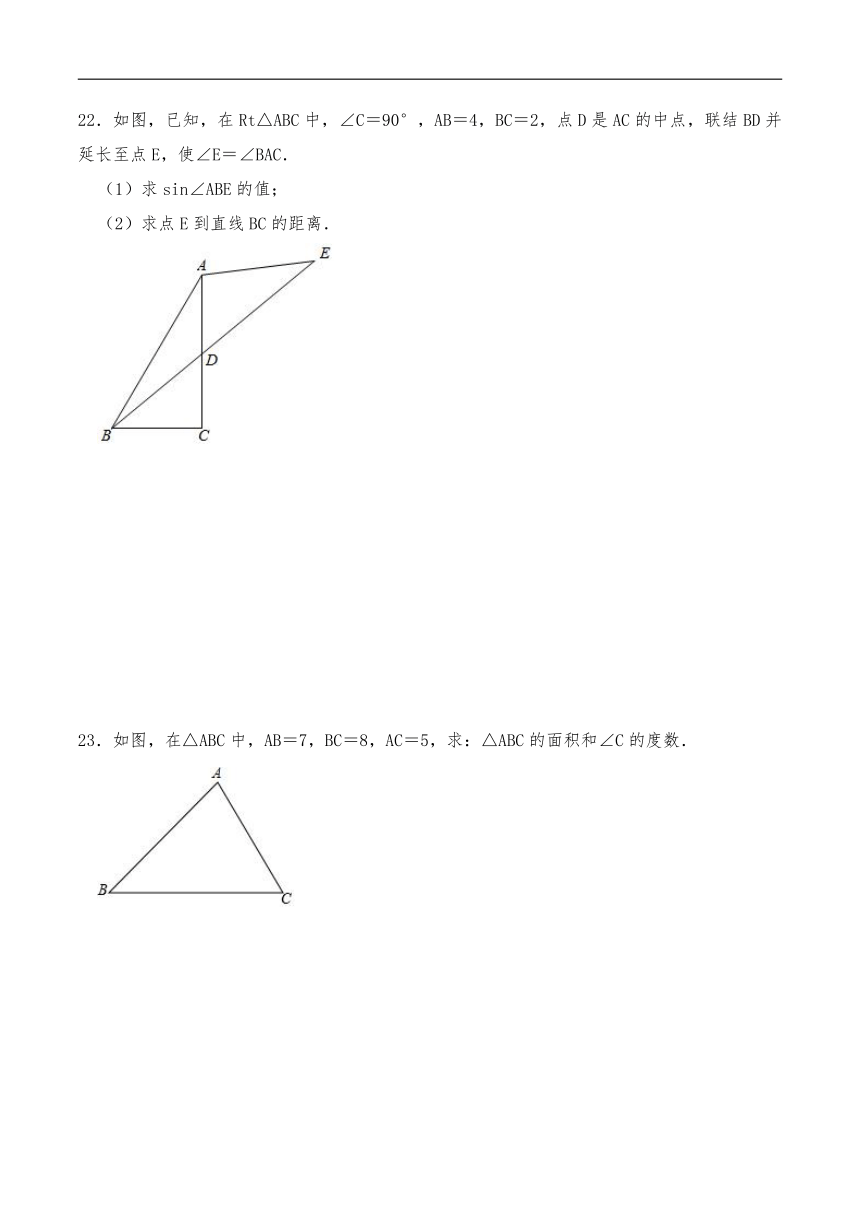
22.如图,已知,在Rt△ABC中,∠C=90°,AB=4,BC=2,点D是AC的中点,联结BD并延长至点E,使∠E=∠BAC.
(1)求sin∠ABE的值;
(2)求点E到直线BC的距离.
23.如图,在△ABC中,AB=7,BC=8,AC=5,求:△ABC的面积和∠C的度数.
24.如图,已知⊙O的半径为,在⊙O中,OA、OB是圆的半径,且OA⊥OB,点C在线段AB的延长线上,且OC=AB.
(1)求线段BC的长;
(2)求∠BOC的正弦值.
答案
一、选择题.
1.
【分析】根据直角三角形的边角关系可得结论.
【解析】在Rt△ABC中,
∵cosB,∠B=50°,AB=10,
∴BC=AB cosB=10 cos50°,
故选:A.
2.
【分析】根据含30°直角三角形的性质得到AB=2BC,BC=2BD,设BD=x,则BC=2x,AB=4x,根据勾股定理求得AC=2x,CDx,逐项代入判断即可得到结论.
【解析】∵∠ACB=90°,∠A=30°,
∴AB=2BC,∠B=60°,
∵CD⊥AB,
∴∠BAC=30°,
∴BC=2BD,
设BD=x,则BC=2x,AB=4x,
∴AC2x,CDx,
∵,
∴A不合题意;
∵,
∴B符合题意;
∵,
∴C不合题意;
∵,
∴D不合题意;
故选:B.
3.
【分析】如图,过P点作PA⊥x轴于A,则∠POA=α,利用P点坐标得到OA=1,PA=3,然后根据正切的定义求出tan∠POA的值即可.
【解析】如图,过P点作PA⊥x轴于A,
则∠POA=α,
∵点P的坐标为(1,3),
∴OA=1,PA=3,
∴tan∠POA3,
即tanα=3.
故选:D.
4.
【分析】在Rt△ABC中,由锐角三角函数的意义可求出AC=m cosα,在Rt△ADC中,由锐角三角函数的意义可求出CD=m cosα sinα,进而得出答案.
【解析】如图,在Rt△ABC中,
∵cosA,AB=m,∠A=α,
∴AC=m cosα,
在Rt△ADC中,
∵sinA,AC=m cosα,∠A=α,
∴CD=m cosα sinα,
故选:B.
5.
【分析】求出∠A,∠B的值即可判断.
【解析】∵sinA,cotB,
∴∠A=30°,∠B=60°,
∴∠C=180°﹣30°﹣60°=90°,
∴△ABC是直角三角形,
故选:D.
6.
【分析】过点C(2,1),作CD⊥x轴于D,则OD=2,CD=1,由三角函数定义即可得出答案.
【解析】过点C(2,1)作CD⊥x轴于D,如图所示:
则OD=2,CD=1,
在Rt△OCD中,tanα.
故选:B.
7.
【分析】根据正切函数的定义求解即可.
【解析】如图,
在Rt∠ACB中,∵∠C=90°,
∴tanB2,
∴2,
∴AC=4.
故选:B.
8.
【分析】根据余切函数的定义解答即可.
【解析】如图,在Rt△ABC中,∵∠C=90°,AC=8,BC=6,
∴cotB,
故选:A.
9.
【分析】过点A作AB⊥x轴,构造直角三角形,由坐标得出OB=2,AB=3,再根据余切的意义求出结果即可.
【解析】过点A作AB⊥x轴,垂足为B,则OB=2,AB=3,
在Rt△OAB中,cot∠AOB=cotα,
故选:B.
10.
【分析】作AE⊥BC于E,根据等腰三角形的性质,解直角三角形得到ACCD,即可得到,然后根据三角形面积公式求得.
【解析】作AE⊥BC于E,
∵AB=AC,
∴BE=ECBC,
∵在Rt△AEC中,cosC,
∴AC=3EC,
∴ACBC,
在Rt△BCD中,cosC,
∴BC=3CD,
∴ACCD,
∴,
∴,
故选:B.
二、填空题
11.
【分析】设AB=k,则AC=2k,BCk,根据勾股定理的逆定理推知△ABC是直角三角形,然后根据锐角三角函数的定义作答.
【解析】根据题意,可设AB=k,则AC=2k,BCk,
∴AC2+AB2=BC2=5k2,
∴△ABC是直角三角形,且∠A=90°.
∴tanB2.
故答案是:2.
12.
【分析】首先作过AAH⊥BC,再利用∠B=60°,AB=5,求出AH,即可得出结果.
【解析】过A作AH⊥BC于H,如图所示:
在Rt△ABH中,∠AHB=90°,∠B=60°,AB=5,
∴sinB,
∴AH=AB sinB=5×sin60°=5,
∴S△ABCAH BC8=10,
故答案为:10.
13.
【分析】由DP⊥AP,CD⊥DP,得AP∥CD,则∠C=∠APB,由tan∠APB,求得BP=4,PC=6,在Rt△CDP中,tanC,CD,得出,即可得出结果.
【解析】∵DP⊥AP,CD⊥DP,
∴AP∥CD,
∴∠C=∠APB,
∵AB⊥BC,
∴tan∠APB,
∵tanC,
∴,
∴BP=4,
∴PC=BC﹣BP=10﹣4=6,
在Rt△CDP中,tanC,CD,
∴,
解得:DP或DP(不合题意舍去),
故答案为:.
14.
【分析】根据题意,作出合适的平面直角坐标系,然后作AB⊥x轴于点B,再根据点的A的坐标和勾股定理,可以得到OA的长,然后即可得到cosθ的值.
【解析】作AB⊥x轴于点B,如右图所示,
∵点A(12,5),
∴OB=12,AB=5,∠ABO=90°,
∴OA13,
∴cos∠AOB,
即cosθ,
故答案为:.
15.
【分析】过A作AD⊥BC,则∠ADB=∠ADC=90°,解直角三角形求出AD和BD,求出CD=AD=4,再求出答案即可.
【解析】过A作AD⊥BC,则∠ADB=∠ADC=90°,
∵sinB,AB=5,
∴AD=4,
由勾股定理得:BD3,
∵BC=7,
∴CD=BC﹣BD=7﹣3=4,
∴AD=CD,
∴∠C=∠CAD=45°,
故答案为:45.
16.
【分析】如图,过点E作EF⊥BC于F,过点A作AH⊥CB交CB的延长线于H.解直角三角形求出BH,CH即可解决问题.
【解析】如图,过点E作EF⊥BC于F,过点A作AH⊥CB交CB的延长线于H.
∵∠ABC=120°,
∴∠ABH=180°﹣∠ABC=60°,
∵AB=12,∠H=90°,
∴BH=AB cos60°=6,AH=AB sin60°=6,
∵EF⊥DF,DE=5,
∴sin∠ADE,
∴EF=4,
∴DF3,
∵S△CDE=6,
∴ CD EF=6,
∴CD=3,
∴CF=CD+DF=6,
∵tanC,
∴,
∴CH=9,
∴BC=CH﹣BH=96.
故答案为:96.
17.
【分析】如图,取格点E,连接AE、BE,通过计算得直角三角形△ABE,利用CD∥BE,得到∠AOC=∠ABE.在Rt△ABE中,依据正切值的意义可求解.
【解析】如图,取格点E,连接AE、BE,
设网格中的小正方形的边长为1,
则BE,
AE.
由网格可以看出:∠AED=45°,∠BED=45°.
∴∠AEB=45°+45°=90°.
同理,∠ACD=90°.
∴CD∥BE.
∴∠AOC=∠ABE.
∴tan∠AOC=tan∠ABE.
在Rt△ABE中,tan∠ABE.
∴tan∠AOC=3.
故答案为:3.
18.
【分析】利用题中的方法构建一个Rt△ADC,使∠D=22.5°,然后利用余切的定义求解.
【解析】作Rt△ABC,使∠C=90°,∠ABC=45°,再延长CB到点D,使BD=BA,联结AD,
∵AB=BD,
∴∠BAD=∠D,
∵∠ABC=∠BAD+∠D,
∴∠D∠ABC=22.5°,
设AC=t,则BC=t,ABt,
∴CD=BC+BD=tt=(1)t,
在Rt△ADC中,cotD1,
∴cot22.5°1.
故答案为1.
三、解答题
19.(1)∵∠ACB=90°,AC=6,cosA,
∴,
∴AB=10,
∴BC8,
又∵D为AB中点,
∴AD=BD=CDAB=5,
∴∠DCB=∠B,
∴cos∠DCB,cos∠B,
∴,
∴CE;
(2)作EF⊥AB交AB于F,
由(1)知CE,
则BE=8,DE,
设BF=x,则DF=BD﹣BF=5﹣x,
在Rt△DEF中,EF2=DE2﹣DF2,
在Rt△BEF中,EF2=BE2﹣BF2,
∴(5﹣x)2x2,
解得x,
∴sin∠BDE.
20.(1)过A作AE⊥BC于E,作DF⊥BC于F,
∵∠BCA=45°,
在Rt△AEC中,AE=EC,
∵cotB,
在Rt△BEA中,,
设BE=3x,AE=2x,
∴BC=BE+EC=BE+AE=10,
∴x=2,
∴BE=6,EA=EC=4,
由勾股定理得:AE2+BE2=AB2.
即AB2=36+16=52.
∴AB.
(2)由(1)知AB=2,
又∵D为AB的中点,
∴BD=AD,
∵DF⊥BC,AE⊥BC,
∴DF∥AE,
∵BD=AD,
∴BF=FEBE=3.
∴DFAE=2,
∴FC=FE+EC=3+4=7.
∴tan∠DCB.
21.(1)过C点作CH⊥AD于H,如图,
∵CD=CA,
∴AH=DH,
∵∠ABC+∠BCH=90°,∠ACH+∠BCH=90°,
∴∠ACH=∠ABC,
∴sin∠ACH=sin∠ABC,
在Rt△ACH中,sin∠ACH,
∴AD=2AH=2;
(2)在Rt△ABC中,sin∠ABC,
∴AB=3AC=9,
∴BD=AB﹣AD=9﹣2=7,
∵∠E=90°,
而∠EDB=∠HDC,
∴∠HCD=∠EBD,
∴sin∠EBD,
∴DEBD,
∴BE,
在Rt△EBC中,tan∠EBC.
22.(1)过D作DF⊥AB于F,如图:
∵∠C=90°,AB=4,BC=2,
∴AC2,sin∠BAC,
∴∠BAC=30°,
∵点D是AC的中点,
∴AD=CD,
∴BD,
Rt△ADF中,DF=AD sin∠BAC,
Rt△BDF中,sin∠ABE;
(2)过A作AH⊥BE于H,过E作EG∥AC交BC延长线于G,如图:
∵∠ADH=∠BDC,∠BCD=∠AHD=90°,
∴△BCD∽△AHD,
∴,
∵BC=2,CD=AD,BD,
∴,解得AH,HD,
∵∠AEB=∠BAC=30°,
∴HE,
∴BE=BD+DH+HE,
∵EG∥AC,
∴∠BDC=∠BEG,
而∠CBD=∠GBE,
∴△CBD∽△GBE,
∴,即,
∴EG.
方法二:过E作EG⊥BC于G,
∵∠E=∠BAC,∠ABE=∠DBA,
∴△ABD∽△ABE,
∴,
即,
∴BE,
∵DC⊥BC,EG⊥BG,
∴DC∥BG,
∴,即,
∴EG,
∴点E到直线BC的距离为.
23.作AD⊥BC于D,
设CD=x,则BD=8﹣x,
由勾股定理可得:,
解得:x=2.5,
即CD=2.5,
∴∠ACD=60°,
∴AD,
∴.
24.(1)如图,过点O作OD⊥AB于点D,
∵OA=OB,∠AOB=90°,
∴AB=OC=2,OD=BD=1,
∴∠C=30°,
∴CD,
∴BC1;
(2)如图,过点B作BE⊥OC于点E,
∵∠C=30°,
∴BEBC,
∴sin∠BOC.
一、选择题.
1.已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么BC的长为( )
A.10cos50° B.10sin50° C.10tan50° D.10cot50°
2.在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,垂足为D,下列四个选项中,不正确的是( )
A. B. C. D.
3.在平面直角坐标系xOy中,已知点P(1,3),点P与原点O的连线与x轴的正半轴的夹角为α(0°<α<90°),那么tanα的值是( )
A. B. C. D.3
4.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A=α,那么CD的长为( )
A.m sinα tanα B.m sinα cosα
C.m cosα tanα D.m cosα cotα
5.在△ABC中,如果sinA,cotB,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
6.如图,直线OA过点(2,1),直线OA与x轴的夹角为α,则tanα的值为( )
A. B. C.2 D.
7.在Rt△ABC中,∠C=90°,如果BC=2,tanB=2,那么AC=( )
A.1 B.4 C. D.2
8.在Rt△ABC中,∠C=90°,如果AC=8,BC=6,那么∠B的余切值为( )
A. B. C. D.
9.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴的夹角α的余切值是( )
A. B. C. D.
10.如图,在等腰△ABC中,AB=AC,BD是AC边上的高,cosC,则△BCD与△ABD的面积比是( )
A.1:3 B.2:7 C.2:9 D.2:11
二、填空题
11.在△ABC中,AB:AC:BC=1:2:,那么tanB= .
12.在△ABC中,AB=5,BC=8,∠B=60°,则△ABC的面积是 .
13.如图,点P在线段BC上,AB⊥BC,DP⊥AP,CD⊥DP,如果BC=10,AB=2,tanC,那么DP的长是 .
14.在直角坐标平面内有一点A(12,5),点A与原点O的连线与x轴的正半轴的夹角为θ,那么cosθ= .
15.已知锐角△ABC中,AB=5,BC=7,sinB,那么∠C= 度.
16.如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE,ED=5,如果△ECD的面积是6,那么BC的长是 .
17.如图,已知在正方形网格中,点A、B、C、D在小正方形的顶点上,线段AB与线段CD相交于点O,那么tan∠AOC= .
18.如图,图中提供了一种求cot15°的方法.作Rt△ABC,使∠C=90°,∠ABC=30°,再延长CB到点D,使BD=BA,联结AD,即可得∠D=15°.如果设AC=t,则可得CD=(2)t,那么cot15°=cotD2.运用以上方法,可求得cot22.5°的值是 .
三、解答题
19.如图,在Rt△ABC中,∠ACB=90°,AC=6,cosA.D是AB边的中点,过点D作直线CD的垂线,与边BC相交于点E.
(1)求线段CE的长;
(2)求sin∠BDE的值.
20.如图,在△ABC中,∠ACB=45°,cotB,BC=10.
(1)求AB的长;
(2)如果CD为边AB上的中线,求∠DCB的正切值.
21.如图,在Rt△ABC中,∠ACB=90°,AC=3,sin∠ABC,D是边AB上一点,且CD=CA,BE⊥CD,垂足为点E.
(1)求AD的长;
(2)求∠EBC的正切值.
22.如图,已知,在Rt△ABC中,∠C=90°,AB=4,BC=2,点D是AC的中点,联结BD并延长至点E,使∠E=∠BAC.
(1)求sin∠ABE的值;
(2)求点E到直线BC的距离.
23.如图,在△ABC中,AB=7,BC=8,AC=5,求:△ABC的面积和∠C的度数.
24.如图,已知⊙O的半径为,在⊙O中,OA、OB是圆的半径,且OA⊥OB,点C在线段AB的延长线上,且OC=AB.
(1)求线段BC的长;
(2)求∠BOC的正弦值.
答案
一、选择题.
1.
【分析】根据直角三角形的边角关系可得结论.
【解析】在Rt△ABC中,
∵cosB,∠B=50°,AB=10,
∴BC=AB cosB=10 cos50°,
故选:A.
2.
【分析】根据含30°直角三角形的性质得到AB=2BC,BC=2BD,设BD=x,则BC=2x,AB=4x,根据勾股定理求得AC=2x,CDx,逐项代入判断即可得到结论.
【解析】∵∠ACB=90°,∠A=30°,
∴AB=2BC,∠B=60°,
∵CD⊥AB,
∴∠BAC=30°,
∴BC=2BD,
设BD=x,则BC=2x,AB=4x,
∴AC2x,CDx,
∵,
∴A不合题意;
∵,
∴B符合题意;
∵,
∴C不合题意;
∵,
∴D不合题意;
故选:B.
3.
【分析】如图,过P点作PA⊥x轴于A,则∠POA=α,利用P点坐标得到OA=1,PA=3,然后根据正切的定义求出tan∠POA的值即可.
【解析】如图,过P点作PA⊥x轴于A,
则∠POA=α,
∵点P的坐标为(1,3),
∴OA=1,PA=3,
∴tan∠POA3,
即tanα=3.
故选:D.
4.
【分析】在Rt△ABC中,由锐角三角函数的意义可求出AC=m cosα,在Rt△ADC中,由锐角三角函数的意义可求出CD=m cosα sinα,进而得出答案.
【解析】如图,在Rt△ABC中,
∵cosA,AB=m,∠A=α,
∴AC=m cosα,
在Rt△ADC中,
∵sinA,AC=m cosα,∠A=α,
∴CD=m cosα sinα,
故选:B.
5.
【分析】求出∠A,∠B的值即可判断.
【解析】∵sinA,cotB,
∴∠A=30°,∠B=60°,
∴∠C=180°﹣30°﹣60°=90°,
∴△ABC是直角三角形,
故选:D.
6.
【分析】过点C(2,1),作CD⊥x轴于D,则OD=2,CD=1,由三角函数定义即可得出答案.
【解析】过点C(2,1)作CD⊥x轴于D,如图所示:
则OD=2,CD=1,
在Rt△OCD中,tanα.
故选:B.
7.
【分析】根据正切函数的定义求解即可.
【解析】如图,
在Rt∠ACB中,∵∠C=90°,
∴tanB2,
∴2,
∴AC=4.
故选:B.
8.
【分析】根据余切函数的定义解答即可.
【解析】如图,在Rt△ABC中,∵∠C=90°,AC=8,BC=6,
∴cotB,
故选:A.
9.
【分析】过点A作AB⊥x轴,构造直角三角形,由坐标得出OB=2,AB=3,再根据余切的意义求出结果即可.
【解析】过点A作AB⊥x轴,垂足为B,则OB=2,AB=3,
在Rt△OAB中,cot∠AOB=cotα,
故选:B.
10.
【分析】作AE⊥BC于E,根据等腰三角形的性质,解直角三角形得到ACCD,即可得到,然后根据三角形面积公式求得.
【解析】作AE⊥BC于E,
∵AB=AC,
∴BE=ECBC,
∵在Rt△AEC中,cosC,
∴AC=3EC,
∴ACBC,
在Rt△BCD中,cosC,
∴BC=3CD,
∴ACCD,
∴,
∴,
故选:B.
二、填空题
11.
【分析】设AB=k,则AC=2k,BCk,根据勾股定理的逆定理推知△ABC是直角三角形,然后根据锐角三角函数的定义作答.
【解析】根据题意,可设AB=k,则AC=2k,BCk,
∴AC2+AB2=BC2=5k2,
∴△ABC是直角三角形,且∠A=90°.
∴tanB2.
故答案是:2.
12.
【分析】首先作过AAH⊥BC,再利用∠B=60°,AB=5,求出AH,即可得出结果.
【解析】过A作AH⊥BC于H,如图所示:
在Rt△ABH中,∠AHB=90°,∠B=60°,AB=5,
∴sinB,
∴AH=AB sinB=5×sin60°=5,
∴S△ABCAH BC8=10,
故答案为:10.
13.
【分析】由DP⊥AP,CD⊥DP,得AP∥CD,则∠C=∠APB,由tan∠APB,求得BP=4,PC=6,在Rt△CDP中,tanC,CD,得出,即可得出结果.
【解析】∵DP⊥AP,CD⊥DP,
∴AP∥CD,
∴∠C=∠APB,
∵AB⊥BC,
∴tan∠APB,
∵tanC,
∴,
∴BP=4,
∴PC=BC﹣BP=10﹣4=6,
在Rt△CDP中,tanC,CD,
∴,
解得:DP或DP(不合题意舍去),
故答案为:.
14.
【分析】根据题意,作出合适的平面直角坐标系,然后作AB⊥x轴于点B,再根据点的A的坐标和勾股定理,可以得到OA的长,然后即可得到cosθ的值.
【解析】作AB⊥x轴于点B,如右图所示,
∵点A(12,5),
∴OB=12,AB=5,∠ABO=90°,
∴OA13,
∴cos∠AOB,
即cosθ,
故答案为:.
15.
【分析】过A作AD⊥BC,则∠ADB=∠ADC=90°,解直角三角形求出AD和BD,求出CD=AD=4,再求出答案即可.
【解析】过A作AD⊥BC,则∠ADB=∠ADC=90°,
∵sinB,AB=5,
∴AD=4,
由勾股定理得:BD3,
∵BC=7,
∴CD=BC﹣BD=7﹣3=4,
∴AD=CD,
∴∠C=∠CAD=45°,
故答案为:45.
16.
【分析】如图,过点E作EF⊥BC于F,过点A作AH⊥CB交CB的延长线于H.解直角三角形求出BH,CH即可解决问题.
【解析】如图,过点E作EF⊥BC于F,过点A作AH⊥CB交CB的延长线于H.
∵∠ABC=120°,
∴∠ABH=180°﹣∠ABC=60°,
∵AB=12,∠H=90°,
∴BH=AB cos60°=6,AH=AB sin60°=6,
∵EF⊥DF,DE=5,
∴sin∠ADE,
∴EF=4,
∴DF3,
∵S△CDE=6,
∴ CD EF=6,
∴CD=3,
∴CF=CD+DF=6,
∵tanC,
∴,
∴CH=9,
∴BC=CH﹣BH=96.
故答案为:96.
17.
【分析】如图,取格点E,连接AE、BE,通过计算得直角三角形△ABE,利用CD∥BE,得到∠AOC=∠ABE.在Rt△ABE中,依据正切值的意义可求解.
【解析】如图,取格点E,连接AE、BE,
设网格中的小正方形的边长为1,
则BE,
AE.
由网格可以看出:∠AED=45°,∠BED=45°.
∴∠AEB=45°+45°=90°.
同理,∠ACD=90°.
∴CD∥BE.
∴∠AOC=∠ABE.
∴tan∠AOC=tan∠ABE.
在Rt△ABE中,tan∠ABE.
∴tan∠AOC=3.
故答案为:3.
18.
【分析】利用题中的方法构建一个Rt△ADC,使∠D=22.5°,然后利用余切的定义求解.
【解析】作Rt△ABC,使∠C=90°,∠ABC=45°,再延长CB到点D,使BD=BA,联结AD,
∵AB=BD,
∴∠BAD=∠D,
∵∠ABC=∠BAD+∠D,
∴∠D∠ABC=22.5°,
设AC=t,则BC=t,ABt,
∴CD=BC+BD=tt=(1)t,
在Rt△ADC中,cotD1,
∴cot22.5°1.
故答案为1.
三、解答题
19.(1)∵∠ACB=90°,AC=6,cosA,
∴,
∴AB=10,
∴BC8,
又∵D为AB中点,
∴AD=BD=CDAB=5,
∴∠DCB=∠B,
∴cos∠DCB,cos∠B,
∴,
∴CE;
(2)作EF⊥AB交AB于F,
由(1)知CE,
则BE=8,DE,
设BF=x,则DF=BD﹣BF=5﹣x,
在Rt△DEF中,EF2=DE2﹣DF2,
在Rt△BEF中,EF2=BE2﹣BF2,
∴(5﹣x)2x2,
解得x,
∴sin∠BDE.
20.(1)过A作AE⊥BC于E,作DF⊥BC于F,
∵∠BCA=45°,
在Rt△AEC中,AE=EC,
∵cotB,
在Rt△BEA中,,
设BE=3x,AE=2x,
∴BC=BE+EC=BE+AE=10,
∴x=2,
∴BE=6,EA=EC=4,
由勾股定理得:AE2+BE2=AB2.
即AB2=36+16=52.
∴AB.
(2)由(1)知AB=2,
又∵D为AB的中点,
∴BD=AD,
∵DF⊥BC,AE⊥BC,
∴DF∥AE,
∵BD=AD,
∴BF=FEBE=3.
∴DFAE=2,
∴FC=FE+EC=3+4=7.
∴tan∠DCB.
21.(1)过C点作CH⊥AD于H,如图,
∵CD=CA,
∴AH=DH,
∵∠ABC+∠BCH=90°,∠ACH+∠BCH=90°,
∴∠ACH=∠ABC,
∴sin∠ACH=sin∠ABC,
在Rt△ACH中,sin∠ACH,
∴AD=2AH=2;
(2)在Rt△ABC中,sin∠ABC,
∴AB=3AC=9,
∴BD=AB﹣AD=9﹣2=7,
∵∠E=90°,
而∠EDB=∠HDC,
∴∠HCD=∠EBD,
∴sin∠EBD,
∴DEBD,
∴BE,
在Rt△EBC中,tan∠EBC.
22.(1)过D作DF⊥AB于F,如图:
∵∠C=90°,AB=4,BC=2,
∴AC2,sin∠BAC,
∴∠BAC=30°,
∵点D是AC的中点,
∴AD=CD,
∴BD,
Rt△ADF中,DF=AD sin∠BAC,
Rt△BDF中,sin∠ABE;
(2)过A作AH⊥BE于H,过E作EG∥AC交BC延长线于G,如图:
∵∠ADH=∠BDC,∠BCD=∠AHD=90°,
∴△BCD∽△AHD,
∴,
∵BC=2,CD=AD,BD,
∴,解得AH,HD,
∵∠AEB=∠BAC=30°,
∴HE,
∴BE=BD+DH+HE,
∵EG∥AC,
∴∠BDC=∠BEG,
而∠CBD=∠GBE,
∴△CBD∽△GBE,
∴,即,
∴EG.
方法二:过E作EG⊥BC于G,
∵∠E=∠BAC,∠ABE=∠DBA,
∴△ABD∽△ABE,
∴,
即,
∴BE,
∵DC⊥BC,EG⊥BG,
∴DC∥BG,
∴,即,
∴EG,
∴点E到直线BC的距离为.
23.作AD⊥BC于D,
设CD=x,则BD=8﹣x,
由勾股定理可得:,
解得:x=2.5,
即CD=2.5,
∴∠ACD=60°,
∴AD,
∴.
24.(1)如图,过点O作OD⊥AB于点D,
∵OA=OB,∠AOB=90°,
∴AB=OC=2,OD=BD=1,
∴∠C=30°,
∴CD,
∴BC1;
(2)如图,过点B作BE⊥OC于点E,
∵∠C=30°,
∴BEBC,
∴sin∠BOC.
