沪教版九年级数学上册试题 25.4解直角三角形的应用--仰角俯角问题同步测试(含解析)
文档属性
| 名称 | 沪教版九年级数学上册试题 25.4解直角三角形的应用--仰角俯角问题同步测试(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 418.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 17:46:08 | ||
图片预览


文档简介
25.4解直角三角形的应用--仰角俯角问题
一、选择题.
1.如果小丽在楼上点A处看到楼下点B处小明的俯角是35°,那么点B处小明看点A处小丽的仰角是( )
A.35° B.45° C.55° D.65°
2.直角梯形ABCD如图放置,AB、CD为水平线,BC⊥AB,如果∠BCA=67°,从低处A处看高处C处,那么点C在点A的( )
A.俯角67°方向 B.俯角23°方向
C.仰角67°方向 D.仰角23°方向
3.跳伞运动员小李在200米的空中测得地面上的着落点A的俯角为60°,那么此时小李离着落点A的距离是( )
A.200米 B.400米 C.米 D.米
4.如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m千米后到达点B处,又测得标志物P的俯角为β,那么此时飞机离地面的高度为( )
A.千米 B.千米
C.千米 D.千米
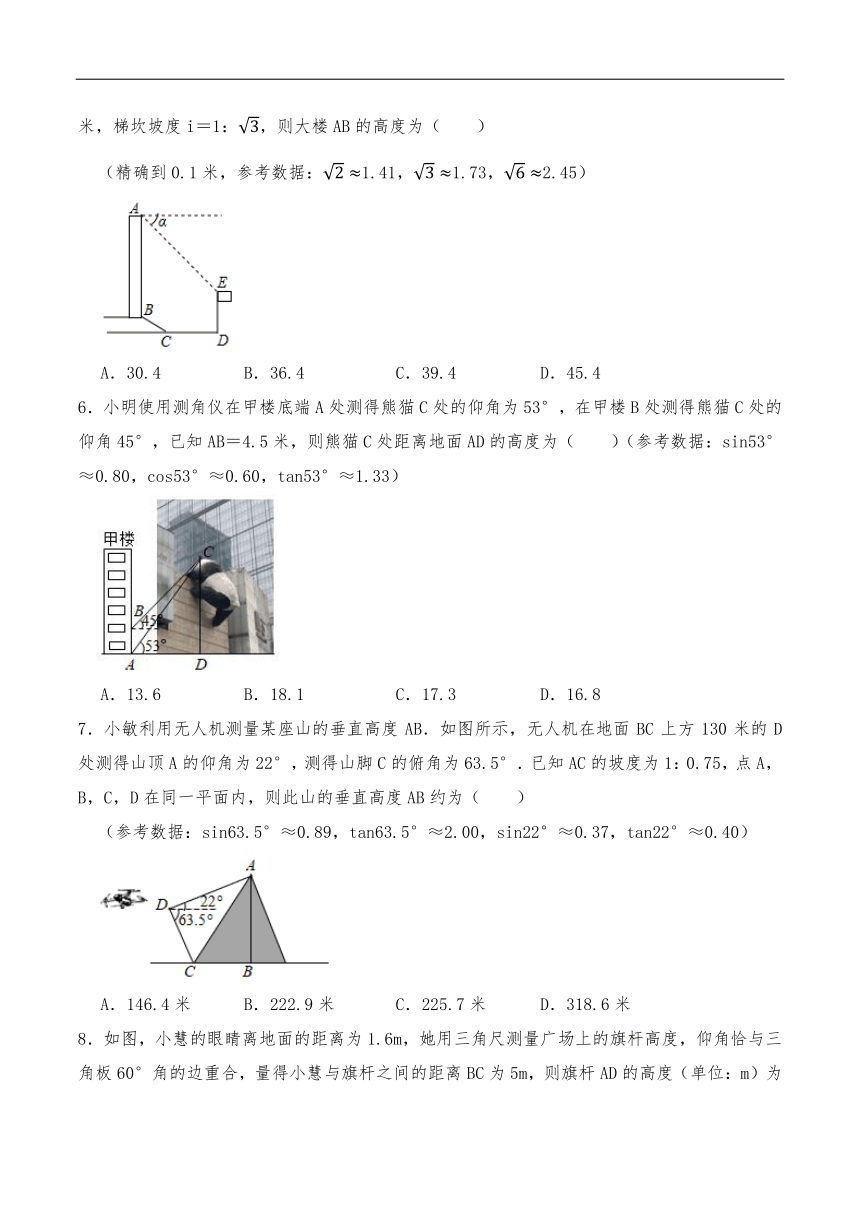
5.如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度为( )
(精确到0.1米,参考数据:1.41,1.73,2.45)
A.30.4 B.36.4 C.39.4 D.45.4
6.小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角45°,已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
A.13.6 B.18.1 C.17.3 D.16.8
7.小敏利用无人机测量某座山的垂直高度AB.如图所示,无人机在地面BC上方130米的D处测得山顶A的仰角为22°,测得山脚C的俯角为63.5°.已知AC的坡度为1:0.75,点A,B,C,D在同一平面内,则此山的垂直高度AB约为( )
(参考数据:sin63.5°≈0.89,tan63.5°≈2.00,sin22°≈0.37,tan22°≈0.40)
A.146.4米 B.222.9米 C.225.7米 D.318.6米
8.如图,小慧的眼睛离地面的距离为1.6m,她用三角尺测量广场上的旗杆高度,仰角恰与三角板60°角的边重合,量得小慧与旗杆之间的距离BC为5m,则旗杆AD的高度(单位:m)为( )
A.6.6 B.11.6 C. D.
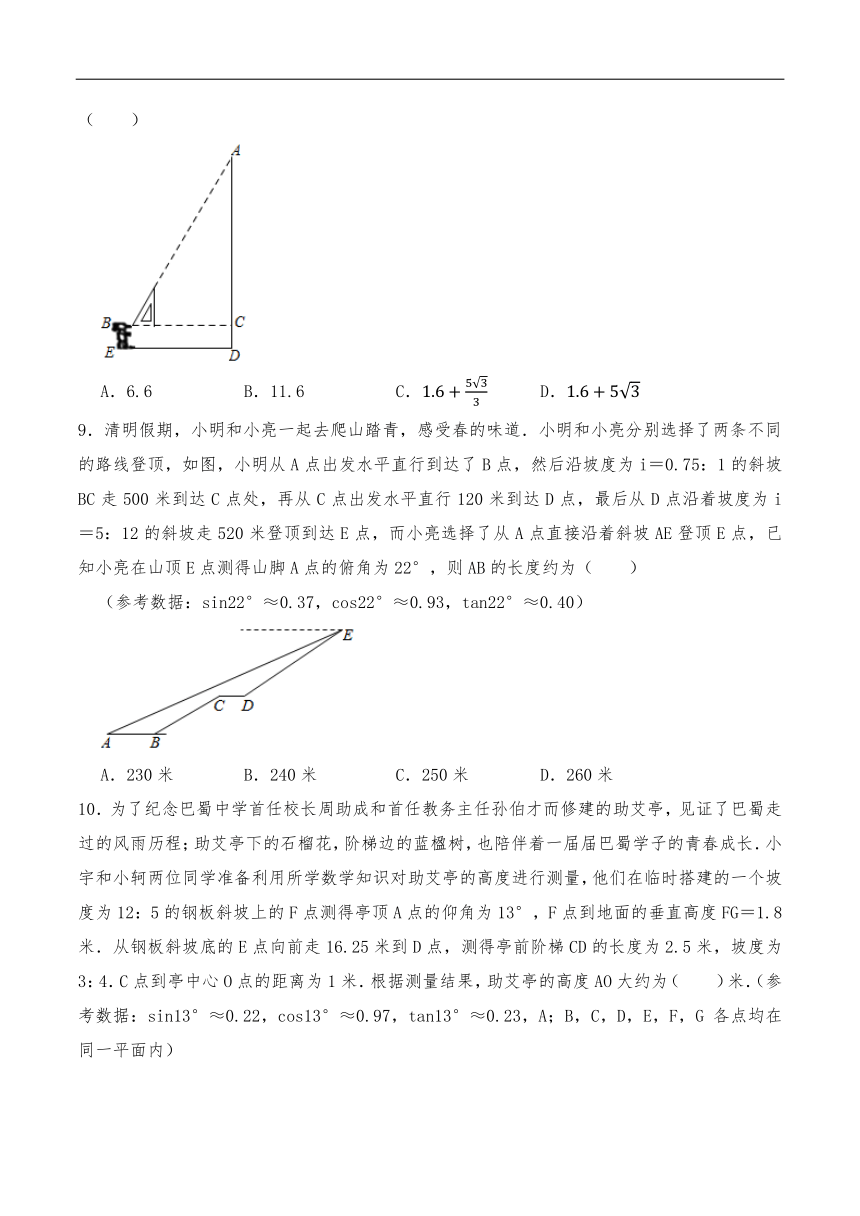
9.清明假期,小明和小亮一起去爬山踏青,感受春的味道.小明和小亮分别选择了两条不同的路线登顶,如图,小明从A点出发水平直行到达了B点,然后沿坡度为i=0.75:1的斜坡BC走500米到达C点处,再从C点出发水平直行120米到达D点,最后从D点沿着坡度为i=5:12的斜坡走520米登顶到达E点,而小亮选择了从A点直接沿着斜坡AE登顶E点,已知小亮在山顶E点测得山脚A点的俯角为22°,则AB的长度约为( )
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
A.230米 B.240米 C.250米 D.260米
10.为了纪念巴蜀中学首任校长周助成和首任教务主任孙伯才而修建的助艾亭,见证了巴蜀走过的风雨历程;助艾亭下的石榴花,阶梯边的蓝楹树,也陪伴着一届届巴蜀学子的青春成长.小宇和小轲两位同学准备利用所学数学知识对助艾亭的高度进行测量,他们在临时搭建的一个坡度为12:5的钢板斜坡上的F点测得亭顶A点的仰角为13°,F点到地面的垂直高度FG=1.8米.从钢板斜坡底的E点向前走16.25米到D点,测得亭前阶梯CD的长度为2.5米,坡度为3:4.C点到亭中心O点的距离为1米.根据测量结果,助艾亭的高度AO大约为( )米.(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,A;B,C,D,E,F,G各点均在同一平面内)
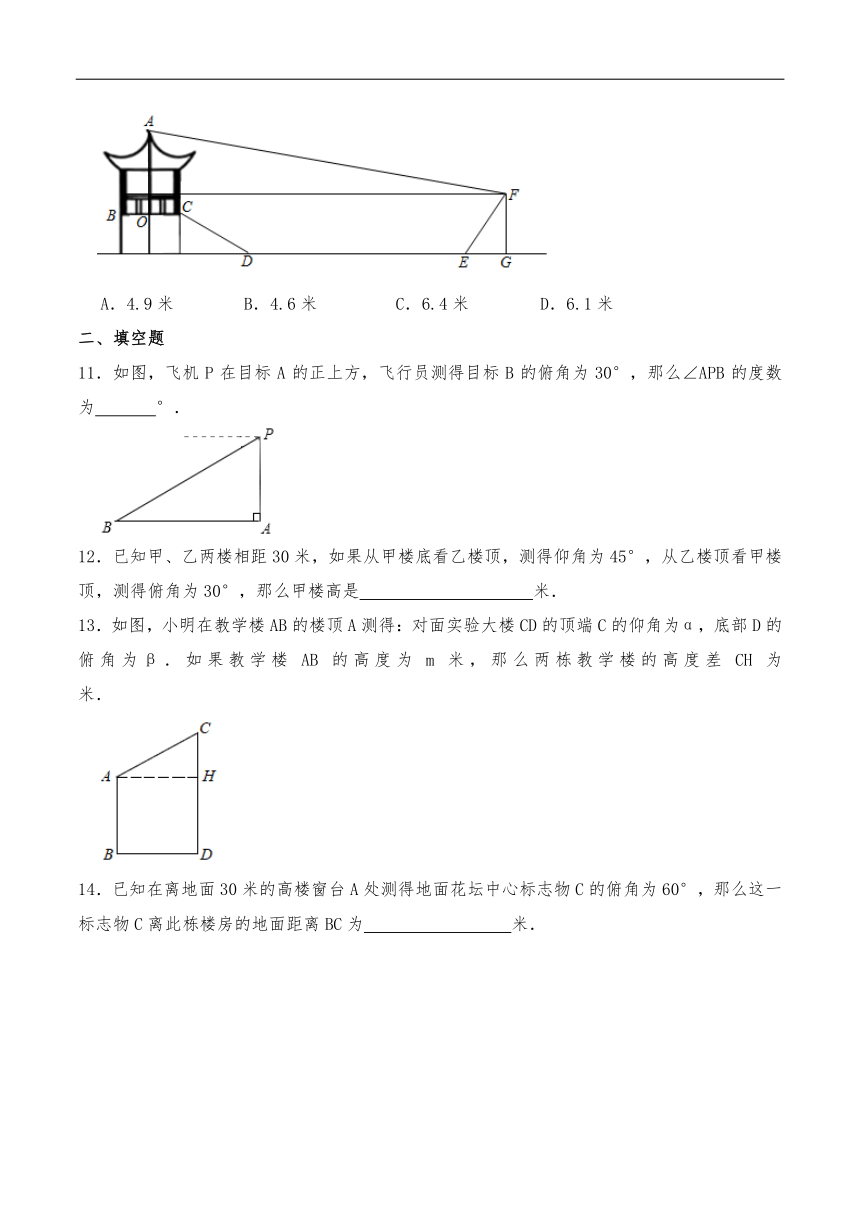
A.4.9米 B.4.6米 C.6.4米 D.6.1米
二、填空题
11.如图,飞机P在目标A的正上方,飞行员测得目标B的俯角为30°,那么∠APB的度数为 °.
12.已知甲、乙两楼相距30米,如果从甲楼底看乙楼顶,测得仰角为45°,从乙楼顶看甲楼顶,测得俯角为30°,那么甲楼高是 米.
13.如图,小明在教学楼AB的楼顶A测得:对面实验大楼CD的顶端C的仰角为α,底部D的俯角为β.如果教学楼AB的高度为m米,那么两栋教学楼的高度差CH为 米.
14.已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为 米.
15.如图,在坡度为1:2.4的斜坡上有一棵与水平面垂直的树BC,在斜坡底部A处测得树顶C的仰角为30°,AB的长为65米,那么树高BC等于 米(保留根号).
16.如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20米,则2号楼的高度为 米(结果保留根号).
17.如图,飞机于空中A处观测其正前方地面控制点C的俯角为30°,若飞机航向不变,继续向前飞行1000米至B处时,观测到其正前方地面控制点C的俯角为45°,那么该飞机与地面的高度是 米(保留根号).
18.为了测量某建筑物BE的高度(如图),小明在离建筑物15米(即DE=15米)的A处,用测角仪测得建筑物顶部B的仰角为45°,已知测角仪高AD=1.8米,则BE= 米.
三、解答题
19.图1是某地摩天轮的图片,图2是示意图.已知线段BC经过圆心D且垂直于地面,垂足为点C,当座舱在点A时,测得摩天轮顶端点B的仰角为15°,同时测得点C的俯角为76°,又知摩天轮的半径为10米,求摩天轮顶端B与地面的距离.(精确到1米)
参考数据:sin15°≈0.26,cos15°≈0.96,tan15°≈0.27,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01.
20.如图,在距某输电铁塔GH(GH垂直地面)的底部点H左侧水平距离60米的点B处有一个山坡,山坡AB的坡度i=1:,山坡坡底点B到坡顶A的距离AB等于40米,在坡顶A处测得铁塔顶点G的仰角为30°(铁塔GH与山坡AB在同一平面内).
(1)求山坡的高度;
(2)求铁塔的高度GH.(结果保留根号)
21.为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).
(1)求限速道路AB的长(精确到1米);
(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,1.73)
22.某校数学兴趣小组为了测量建筑物CD的高度,先在斜坡AB的底部A测得建筑物顶点C的仰角为31°,再沿斜坡AB走了26m到达斜坡顶点B处,然后在点B测得建筑物顶点C的仰角为53°,已知斜坡AB的坡度i=1:2.4.(参考数据:tan53°,tan31°)
(1)求点B到地面的高度;
(2)求建筑物CD的高度.
23.如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D,点E的俯角分别为64°和53°.已知椅面宽BE=46cm,求椅脚高ED的长(结果取整数).
参考数据:tan53°≈1.33,sin53°≈0.80,tan64°≈2.05,sin64°≈0.90.
24.如图,在数学综合实践活动课上,两名同学要测量小河对岸大树BC的高度,甲同学在点A测得大树顶端B的仰角为45°,乙同学从A点出发沿斜坡走6米到达斜坡上点D,在此处测得树顶端点B的仰角为26.7°,且斜坡AF的坡度为1:2.
(1)求乙同学从点A到点D的过程中上升的高度;
(2)依据他们测量的数据求出大树BC的高度.
(参考数据:sin26.7°≈0.45,cos26.7°≈0.89,tan26.7°≈0.50)
答案
一、选择题.
1.
【分析】根据两点之间的仰角与俯角正好是两条水平线夹角的内错角,应相等即可得结论.
【解析】因为从点A看点B的仰角与从点B看点A的俯角互为内错角,大小相等.
所以小丽在楼上点A处看到楼下点B处小明的俯角是35°,
点B处小明看点A处小丽的仰角是35°.
故选:A.
2.
【分析】求出∠BAC=23°,即可得出答案.
【解析】∵BC⊥AB,∠BCA=67°,
∴∠BAC=90°﹣∠BCA=23°,
从低处A处看高处C处,那么点C在点A的仰角23°方向;
故选:D.
3.
【分析】已知直角三角形的一个锐角和直角边求斜边,运用三角函数定义解答.
【解析】根据题意,此时小李离着落点A的距离是,
故选:D.
4.
【分析】根据题意,作出合适的辅助线,然后根据锐角三角函数即可表示出此时飞机离地面的高度.
【解析】作PC⊥AB交AB于点C,如右图所示,
AC,BC,
∵m=AC﹣BC,
∴m,
∴PC,
故选:A.
5.
【分析】延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CHx米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=(620)(米),即可得出大楼AB的高度.
【解析】如图,延长AB交DC于H,作EG⊥AB于G,
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:,
∴BH:CH=1:,
设BH=x米,则CHx米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+(x)2=122,
解得:x=6,
∴BH=6米,CH=6米,
∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=(620)(米),
∵∠α=45°,
∴∠EAG=90°﹣45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=(620)(米),
∴AB=AG+BG=620+9≈39.4(米);
故选:C.
6.
【分析】过点B作BE⊥CD于点E,根据已知条件求出BE=AD,设CE=x米,则CD=BC+BD=(x+4.5)米,根据锐角三角函数求出x的值,即可得出CD的值.
【解析】如图,过点B作BE⊥CD于点E,
由题意可知:
∵∠CBE=45°,∠CAD=53°,AB=4.5米,
∵∠ABE=∠BED=∠ADE=90°,
∴四边形ABED是矩形,
∴BE=AD,DE=AB=4.5米,
设CE=x米,则CD=BC+BD=(x+4.5)米,
在Rt△CEB中,BEx米,
在Rt△ADC中,CD=AD tan53°,
即x+4.5=x tan53°,
∴x≈13.64,
∴CE=13.64(米),
∴CD=CE+DE=13.64+4.5=18.14≈18.1(米).
答:熊猫C处距离地面AD的高度为18.1米.
故选:B.
7.
【分析】如图,过点D作DH⊥AB于H,过点C作CR⊥DH于R,设AB=x米,则AH=(x﹣130)米.构建方程求解即可.
【解析】如图,过点D作DH⊥AB于H,过点C作CR⊥DH于R,设AB=x米,则AH=(x﹣130)米.
∵AB:BC=1:0.75,
∴BC=RH=0.75x(米),BH=CR=130米,
在Rt△DCR中,DR65(米),
∵tan∠ADH,
∴0.4,
解得x≈222.9,
∴AB=222.9(米),
故选:B.
8.
【分析】利用直角三角形的一边与AC平行得到∠ABC=60°,则根据含30度的直角三角形三边的关系得到AC,然后计算AC+CD即可.
【解析】根据题意得∠ABC=60°,
在Rt△ABC中,ACBC=5m,
所以AD=AC+CD=(51.6)m.
答:旗杆的高度(51.6)m.
故选:D.
9.
【分析】通过作垂线和平行线,构造直角三角形,利用坡度和直角三角形的边角关系可求出答案.
【解析】如图,过C、E分别作CF⊥AB、EG⊥AB,垂足为F、G,延长CD交EG于点H,
由斜坡BC的坡度i=0.75:1,即i=3:4,BC=500,
设CF=3x米,则BF=4x米,由勾股定理可得,
CF2+BF2=BC2,
即(3x)2+(4x)2=5002,
解得,x=100(米),
∴GF=300(米),BF=400(米),
由斜坡DE的坡度i=5:12,BC=520米,
设EH=5y米,则DH=12y米,由勾股定理可得,
EH2+DH2=DE2,
即(5y)2+(12)2=5202,
解得,y=40(米),
∴EH=5y=200(米),DH=12y=480(米),
∴EG=EH+HG=200+300=500(米),
BG=BF+CD+DH=400+120+480=1000(米),
在Rt△AEG中,
∵tan22°,即0.40,
∴AB=250(米),
故选:C.
10.
【分析】由题意可知四边形MNGF是矩形,在RtCDH中,根据勾股定理求得DH=2,在RtEFG中,根据条件可求得EG=0.75,进而求出FM=20,在RtAMF中,根据三角函数的定义求出AM=4.6,进而可求出AO.
【解析】由题意可知,∠AFM=13°,CD=2.5.CD的坡比是3:4,EF的坡比是12:5,FG=1.8,DE=16.25,MF∥NG,ON⊥NG,CH⊥NG,FG⊥NG,OC=NH=1,
∴四边形MNGF是矩形,
∴FM=NG,
在RtCDH中,设CH=3x,DH=4x,
∴CD=2.5,
∴(3x)2+(4x)2=2.52,
∴x=0.5,
∴DH=2,CH=1.5,
在RtEFG中,,FG=1.8,
∴,
∴EG=0.75,
∴FM=GN=EG+DE+DH+NH=20,
在RtAMF中,tan∠AFMtan13°,
∴AM≈20×0.23=4.6,
∴AO=AM+MO=AM+(FG=CH)=4.9(米),
答:助艾亭的高度AO大约为4.9米.
故选:A.
二、填空题
11.
【分析】根据题意可得∠PAB=90°,∠B=30°,进而根据直角三角形两个锐角互余可得结果.
【解析】根据题意可知:
∠PAB=90°,∠B=30°,
∴∠APB=90°﹣30°=60°.
故答案为:60.
12.
【分析】过C作CE⊥AB于E,先由矩形和含30°角的直角三角形的性质求出AE的长,再由等腰直角三角形的性质求出AB的长,即可得出结果.
【解析】如图,甲楼为CD、乙楼为AB,BD=30米,∠ADB=45°,∠CAF=30°,
过C作CE⊥AB于E,则四边形BDCE为矩形,CE∥AF,
∴CE=BD=30米,CD=BE,∠ACE=∠CAF=30°,
∴AECE=10(米),
在Rt△ABD中,∠ADB=45°,
∴△ABD为等腰直角三角形,
∴BD=AB=30米,
∴CD=BE=AB﹣AE=(30﹣10)米,
即甲楼的高为(30﹣10)米,
故答案为:(30﹣10).
13.
【分析】根据正切的定义分别求出DH、CH,结合图形计算即可.
【解析】连接AD,过点A作AH⊥CD于点H,则四边形ABDH是矩形,
∴AB=DH=m米,
在Rt△ADH中,∠DAH=β,
∴tanβ,
∴AH,
在Rt△ACH中,∠CAH=α,
∴CH=AH tanα tanα(米),
答:两栋教学楼的高度差CH为米.
故答案为:.
14.
【分析】利用解直角三角形的知识知一边和角求另一边即可.
【解析】根据题意得到AB=30米,∠BAC=30°,
∵AB⊥BC,
∴BC=AB tan30°=3010米,
∴标志物C离此栋楼房的地面距离BC为10米,
故答案为10.
15.
【分析】延长CB交水平面于点D,根据题意可得CD⊥AD,再根据坡度可得BD:AD=1:2.4,根据勾股定理可得BD=25,AD=60,最后根据锐角三角函数即可求出CB的长.
【解析】如图,延长CB交水平面于点D,
根据题意可知:
CD⊥AD,
∴∠ADC=90°,
在Rt△ADB中,AB=65,
∵BD:AD=1:2.4,
∴AD=2.4BD,
根据勾股定理,得
AD2+BD2=AB2,
即BD2+(2.4BD)2=652,
解得BD=25,
∴AD=60,
在Rt△ACD中,∠CAD=30°,
∴tan30°,
即,
解得CB=2025(米).
答:树高BC等于(2025)米.
故答案为:(2025).
16.
【分析】过点E作EG⊥AB于G,过点F作FH⊥AB于H,可得四边形ECBG,HBDF是矩形,在Rt△AEG中,根据三角函数求得EG,在Rt△AHP中,根据三角函数求得AH,再根据线段的和差关系即可求解.
【解析】过点E作EG⊥AB于G,过点F作FH⊥AB于H,
则四边形ECBG,HBDF是矩形,
∴EC=GB=20,HB=FD,
∵B为CD的中点,
∴EG=CB=BD=HF,
由已知得:∠EAG=90°﹣60°=30°,∠AFH=45°.
在Rt△AEG中,AG=AB﹣GB=50﹣20=30米,
∴EG=AG tan30°=3010米,
在Rt△AHP中,AH=HF tan45°=10米,
∴FD=HB=AB﹣AH=50﹣10(米).
答:2号楼的高度为(50﹣10)米.
故答案为:(50﹣10).
17.
【分析】易得CD=BD,那么利用30°的正切值即可求得BD长,即为飞机与地面的高度.
【解析】作CD⊥AB于点D.
∴∠BDC=90°,
∵∠DBC=45°,
∴BD=CD,
∵∠DAC=30°,
∴tan30°,
解得CD=BD=500500(米).
答:该飞机与地面的高度是(500500)米.
故答案为:(500500).
18.
【分析】在Rt△ABC中,已知角的邻边求对边,可以用正切求BC,再加上CE即可.
【解析】过A作AC⊥BE于C,
则AC=DE=15,
根据题意:在Rt△ABC中,有BC=AC×tan45°=15,
则BE=BC+CE=16.8(米),
故答案为:16.8.
三、解答题
19.连接AB、AD、AC,过点A作AE⊥BC于E,
则∠AEB=∠AEC=90°,
由题意得:点A、B在圆D上,
∴DB=DA,
在Rt△ABE中,∠BAE=15°,
∴∠DBA=∠DAB=75°,∠DAE=60°,
∵DA=10米,
∴AE=5(米),
∴BE=AE×tan15°≈5×0.27=1.35(米),
∵∠EAC=76°,
∴CE=AE×tan76°≈5×4.01=20.05(米),
∴BC=BE+CE=1.35+20.05≈21(米),
答:摩天轮顶端B与地面的距离约为21米.
20.(1)过点A作AD垂直HB,交HB的延长线于点D,
即∠ADB=90°,
由题意得:i=1:,AB=60(米),
∴,
即;
又∵AB2=AD2+BD2,
即,
∴AD=20(米),
答:山坡的高度为20米;
(2)作AE∥BH交GH于点E,
∵AD⊥BH,GH⊥BH,
∴AD∥GH,
即:四边形ADHE是平行四边形,
由题意可知:∠GAE=30°,BH=60(米),
∵(米),
∴(米),
在Rt△AGE中,,
∴(米),
又∵EH=AD=20(米),
∴(米),
答:铁塔的高度GH为米.
21.(1)根据题意,得∠CAB=37°,CD=220米,∠DAB=30°,∠DBA=45°,
如图,过点C和点D作CE和DF垂直于AB于点E和F,
∵CD∥AB,
∴四边形CDFE是矩形,
∴CE=DF,CD=EF,
∵∠DBA=45°,
∴DF=BF,
设DF=BF=CE=x米,
在Rt△ADF中,∠DAF=30°,DF=x米,
∴AFDFx(米),
∴AE=AF﹣EF=(x﹣220)米,
在Rt△AEC中,∠CAE=37°,
∵CE=AE tan37°,
∴x=(x﹣220)×0.75,
解得x=60(34)=(180240)米,
∴AEx﹣220=(320+240)米,
FB=x=(180240)(米),
∴AB=AE+EF+FB
=320+240220+180240
=780+420
≈1507(米),
答:限速道路AB的长约为1507米;
(2)∵1分20秒小时,
∴该汽车的速度约为:150767.8km/h>60km/h,
∴该车超速.
22.(1)过点B作BE⊥AD于点E,BF⊥CD于点F,
在Rt△ABE中,BE:AE=1:2.4=5:12,
设BE=5xm,AE=12xm,
在Rt△ABE中,由勾股定理得:AB13x(m),
∴13x=26,
解得:x=2(m),
∴BE=FD=5x=10(m),
∴点B到地面的高度为10m;
(2)AE=12x=24(m),
过点B作BF⊥CD于点F,
∵CD⊥AD,
∴四边形BEDF是矩形,
∴DF=BE=10m,BF=DE,
∵tan∠CBF,
∴BFCF=DE,
∵tan∠CAD,
∴,
即:,
解得:CF=8(m),
∴CD=DF+CF=10+8=18(m).
23.∵AC⊥BE,AC⊥CD,AC∥ED,
∴四边形BCDE是矩形,
∴BC=DE,CD=BE=46cm,
由题意可得∠AEB=53°,∠ADC=64°,
在Rt△ABE中,tan53°,
∴AB=BEtan53°,
在Rt△ACD中,tan64°,
∴AC=CDtan64°,
∴ED=BC=AC﹣AB≈46×2.05﹣46×1.33=94.30﹣61.18=33.12≈33(cm),
答:椅脚高ED的长约为33cm.
24.(1)作DH⊥AE于H,如图所示:
在Rt△ADH中,∵,
∴AH=2DH,
∵AH2+DH2=AD2,
∴(2DH)2+DH2=(6)2,
∴DH=6(米).
答:乙同学从点A到点D的过程中,他上升的高度为6米;
(2)如图所示:过点D作DG⊥BC于点G,设BC=x米,
在Rt△ABC中,∠BAC=45°,
∴AC=BC=x,
由(1)得AH=2DH=12,
在矩形DGCH中,DH=CG=6,DG=CH=AH+AC=x+12,
在Rt△BDG中,BG=BC﹣CG=BC﹣DH=x﹣6,
∵tan∠BDG,
∴0.5,
解得:x=24(米),
答:大树的高度约为24米.
一、选择题.
1.如果小丽在楼上点A处看到楼下点B处小明的俯角是35°,那么点B处小明看点A处小丽的仰角是( )
A.35° B.45° C.55° D.65°
2.直角梯形ABCD如图放置,AB、CD为水平线,BC⊥AB,如果∠BCA=67°,从低处A处看高处C处,那么点C在点A的( )
A.俯角67°方向 B.俯角23°方向
C.仰角67°方向 D.仰角23°方向
3.跳伞运动员小李在200米的空中测得地面上的着落点A的俯角为60°,那么此时小李离着落点A的距离是( )
A.200米 B.400米 C.米 D.米
4.如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m千米后到达点B处,又测得标志物P的俯角为β,那么此时飞机离地面的高度为( )
A.千米 B.千米
C.千米 D.千米
5.如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度为( )
(精确到0.1米,参考数据:1.41,1.73,2.45)
A.30.4 B.36.4 C.39.4 D.45.4
6.小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角45°,已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
A.13.6 B.18.1 C.17.3 D.16.8
7.小敏利用无人机测量某座山的垂直高度AB.如图所示,无人机在地面BC上方130米的D处测得山顶A的仰角为22°,测得山脚C的俯角为63.5°.已知AC的坡度为1:0.75,点A,B,C,D在同一平面内,则此山的垂直高度AB约为( )
(参考数据:sin63.5°≈0.89,tan63.5°≈2.00,sin22°≈0.37,tan22°≈0.40)
A.146.4米 B.222.9米 C.225.7米 D.318.6米
8.如图,小慧的眼睛离地面的距离为1.6m,她用三角尺测量广场上的旗杆高度,仰角恰与三角板60°角的边重合,量得小慧与旗杆之间的距离BC为5m,则旗杆AD的高度(单位:m)为( )
A.6.6 B.11.6 C. D.
9.清明假期,小明和小亮一起去爬山踏青,感受春的味道.小明和小亮分别选择了两条不同的路线登顶,如图,小明从A点出发水平直行到达了B点,然后沿坡度为i=0.75:1的斜坡BC走500米到达C点处,再从C点出发水平直行120米到达D点,最后从D点沿着坡度为i=5:12的斜坡走520米登顶到达E点,而小亮选择了从A点直接沿着斜坡AE登顶E点,已知小亮在山顶E点测得山脚A点的俯角为22°,则AB的长度约为( )
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
A.230米 B.240米 C.250米 D.260米
10.为了纪念巴蜀中学首任校长周助成和首任教务主任孙伯才而修建的助艾亭,见证了巴蜀走过的风雨历程;助艾亭下的石榴花,阶梯边的蓝楹树,也陪伴着一届届巴蜀学子的青春成长.小宇和小轲两位同学准备利用所学数学知识对助艾亭的高度进行测量,他们在临时搭建的一个坡度为12:5的钢板斜坡上的F点测得亭顶A点的仰角为13°,F点到地面的垂直高度FG=1.8米.从钢板斜坡底的E点向前走16.25米到D点,测得亭前阶梯CD的长度为2.5米,坡度为3:4.C点到亭中心O点的距离为1米.根据测量结果,助艾亭的高度AO大约为( )米.(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,A;B,C,D,E,F,G各点均在同一平面内)
A.4.9米 B.4.6米 C.6.4米 D.6.1米
二、填空题
11.如图,飞机P在目标A的正上方,飞行员测得目标B的俯角为30°,那么∠APB的度数为 °.
12.已知甲、乙两楼相距30米,如果从甲楼底看乙楼顶,测得仰角为45°,从乙楼顶看甲楼顶,测得俯角为30°,那么甲楼高是 米.
13.如图,小明在教学楼AB的楼顶A测得:对面实验大楼CD的顶端C的仰角为α,底部D的俯角为β.如果教学楼AB的高度为m米,那么两栋教学楼的高度差CH为 米.
14.已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为 米.
15.如图,在坡度为1:2.4的斜坡上有一棵与水平面垂直的树BC,在斜坡底部A处测得树顶C的仰角为30°,AB的长为65米,那么树高BC等于 米(保留根号).
16.如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20米,则2号楼的高度为 米(结果保留根号).
17.如图,飞机于空中A处观测其正前方地面控制点C的俯角为30°,若飞机航向不变,继续向前飞行1000米至B处时,观测到其正前方地面控制点C的俯角为45°,那么该飞机与地面的高度是 米(保留根号).
18.为了测量某建筑物BE的高度(如图),小明在离建筑物15米(即DE=15米)的A处,用测角仪测得建筑物顶部B的仰角为45°,已知测角仪高AD=1.8米,则BE= 米.
三、解答题
19.图1是某地摩天轮的图片,图2是示意图.已知线段BC经过圆心D且垂直于地面,垂足为点C,当座舱在点A时,测得摩天轮顶端点B的仰角为15°,同时测得点C的俯角为76°,又知摩天轮的半径为10米,求摩天轮顶端B与地面的距离.(精确到1米)
参考数据:sin15°≈0.26,cos15°≈0.96,tan15°≈0.27,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01.
20.如图,在距某输电铁塔GH(GH垂直地面)的底部点H左侧水平距离60米的点B处有一个山坡,山坡AB的坡度i=1:,山坡坡底点B到坡顶A的距离AB等于40米,在坡顶A处测得铁塔顶点G的仰角为30°(铁塔GH与山坡AB在同一平面内).
(1)求山坡的高度;
(2)求铁塔的高度GH.(结果保留根号)
21.为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).
(1)求限速道路AB的长(精确到1米);
(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,1.73)
22.某校数学兴趣小组为了测量建筑物CD的高度,先在斜坡AB的底部A测得建筑物顶点C的仰角为31°,再沿斜坡AB走了26m到达斜坡顶点B处,然后在点B测得建筑物顶点C的仰角为53°,已知斜坡AB的坡度i=1:2.4.(参考数据:tan53°,tan31°)
(1)求点B到地面的高度;
(2)求建筑物CD的高度.
23.如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D,点E的俯角分别为64°和53°.已知椅面宽BE=46cm,求椅脚高ED的长(结果取整数).
参考数据:tan53°≈1.33,sin53°≈0.80,tan64°≈2.05,sin64°≈0.90.
24.如图,在数学综合实践活动课上,两名同学要测量小河对岸大树BC的高度,甲同学在点A测得大树顶端B的仰角为45°,乙同学从A点出发沿斜坡走6米到达斜坡上点D,在此处测得树顶端点B的仰角为26.7°,且斜坡AF的坡度为1:2.
(1)求乙同学从点A到点D的过程中上升的高度;
(2)依据他们测量的数据求出大树BC的高度.
(参考数据:sin26.7°≈0.45,cos26.7°≈0.89,tan26.7°≈0.50)
答案
一、选择题.
1.
【分析】根据两点之间的仰角与俯角正好是两条水平线夹角的内错角,应相等即可得结论.
【解析】因为从点A看点B的仰角与从点B看点A的俯角互为内错角,大小相等.
所以小丽在楼上点A处看到楼下点B处小明的俯角是35°,
点B处小明看点A处小丽的仰角是35°.
故选:A.
2.
【分析】求出∠BAC=23°,即可得出答案.
【解析】∵BC⊥AB,∠BCA=67°,
∴∠BAC=90°﹣∠BCA=23°,
从低处A处看高处C处,那么点C在点A的仰角23°方向;
故选:D.
3.
【分析】已知直角三角形的一个锐角和直角边求斜边,运用三角函数定义解答.
【解析】根据题意,此时小李离着落点A的距离是,
故选:D.
4.
【分析】根据题意,作出合适的辅助线,然后根据锐角三角函数即可表示出此时飞机离地面的高度.
【解析】作PC⊥AB交AB于点C,如右图所示,
AC,BC,
∵m=AC﹣BC,
∴m,
∴PC,
故选:A.
5.
【分析】延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CHx米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=(620)(米),即可得出大楼AB的高度.
【解析】如图,延长AB交DC于H,作EG⊥AB于G,
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:,
∴BH:CH=1:,
设BH=x米,则CHx米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+(x)2=122,
解得:x=6,
∴BH=6米,CH=6米,
∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=(620)(米),
∵∠α=45°,
∴∠EAG=90°﹣45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=(620)(米),
∴AB=AG+BG=620+9≈39.4(米);
故选:C.
6.
【分析】过点B作BE⊥CD于点E,根据已知条件求出BE=AD,设CE=x米,则CD=BC+BD=(x+4.5)米,根据锐角三角函数求出x的值,即可得出CD的值.
【解析】如图,过点B作BE⊥CD于点E,
由题意可知:
∵∠CBE=45°,∠CAD=53°,AB=4.5米,
∵∠ABE=∠BED=∠ADE=90°,
∴四边形ABED是矩形,
∴BE=AD,DE=AB=4.5米,
设CE=x米,则CD=BC+BD=(x+4.5)米,
在Rt△CEB中,BEx米,
在Rt△ADC中,CD=AD tan53°,
即x+4.5=x tan53°,
∴x≈13.64,
∴CE=13.64(米),
∴CD=CE+DE=13.64+4.5=18.14≈18.1(米).
答:熊猫C处距离地面AD的高度为18.1米.
故选:B.
7.
【分析】如图,过点D作DH⊥AB于H,过点C作CR⊥DH于R,设AB=x米,则AH=(x﹣130)米.构建方程求解即可.
【解析】如图,过点D作DH⊥AB于H,过点C作CR⊥DH于R,设AB=x米,则AH=(x﹣130)米.
∵AB:BC=1:0.75,
∴BC=RH=0.75x(米),BH=CR=130米,
在Rt△DCR中,DR65(米),
∵tan∠ADH,
∴0.4,
解得x≈222.9,
∴AB=222.9(米),
故选:B.
8.
【分析】利用直角三角形的一边与AC平行得到∠ABC=60°,则根据含30度的直角三角形三边的关系得到AC,然后计算AC+CD即可.
【解析】根据题意得∠ABC=60°,
在Rt△ABC中,ACBC=5m,
所以AD=AC+CD=(51.6)m.
答:旗杆的高度(51.6)m.
故选:D.
9.
【分析】通过作垂线和平行线,构造直角三角形,利用坡度和直角三角形的边角关系可求出答案.
【解析】如图,过C、E分别作CF⊥AB、EG⊥AB,垂足为F、G,延长CD交EG于点H,
由斜坡BC的坡度i=0.75:1,即i=3:4,BC=500,
设CF=3x米,则BF=4x米,由勾股定理可得,
CF2+BF2=BC2,
即(3x)2+(4x)2=5002,
解得,x=100(米),
∴GF=300(米),BF=400(米),
由斜坡DE的坡度i=5:12,BC=520米,
设EH=5y米,则DH=12y米,由勾股定理可得,
EH2+DH2=DE2,
即(5y)2+(12)2=5202,
解得,y=40(米),
∴EH=5y=200(米),DH=12y=480(米),
∴EG=EH+HG=200+300=500(米),
BG=BF+CD+DH=400+120+480=1000(米),
在Rt△AEG中,
∵tan22°,即0.40,
∴AB=250(米),
故选:C.
10.
【分析】由题意可知四边形MNGF是矩形,在RtCDH中,根据勾股定理求得DH=2,在RtEFG中,根据条件可求得EG=0.75,进而求出FM=20,在RtAMF中,根据三角函数的定义求出AM=4.6,进而可求出AO.
【解析】由题意可知,∠AFM=13°,CD=2.5.CD的坡比是3:4,EF的坡比是12:5,FG=1.8,DE=16.25,MF∥NG,ON⊥NG,CH⊥NG,FG⊥NG,OC=NH=1,
∴四边形MNGF是矩形,
∴FM=NG,
在RtCDH中,设CH=3x,DH=4x,
∴CD=2.5,
∴(3x)2+(4x)2=2.52,
∴x=0.5,
∴DH=2,CH=1.5,
在RtEFG中,,FG=1.8,
∴,
∴EG=0.75,
∴FM=GN=EG+DE+DH+NH=20,
在RtAMF中,tan∠AFMtan13°,
∴AM≈20×0.23=4.6,
∴AO=AM+MO=AM+(FG=CH)=4.9(米),
答:助艾亭的高度AO大约为4.9米.
故选:A.
二、填空题
11.
【分析】根据题意可得∠PAB=90°,∠B=30°,进而根据直角三角形两个锐角互余可得结果.
【解析】根据题意可知:
∠PAB=90°,∠B=30°,
∴∠APB=90°﹣30°=60°.
故答案为:60.
12.
【分析】过C作CE⊥AB于E,先由矩形和含30°角的直角三角形的性质求出AE的长,再由等腰直角三角形的性质求出AB的长,即可得出结果.
【解析】如图,甲楼为CD、乙楼为AB,BD=30米,∠ADB=45°,∠CAF=30°,
过C作CE⊥AB于E,则四边形BDCE为矩形,CE∥AF,
∴CE=BD=30米,CD=BE,∠ACE=∠CAF=30°,
∴AECE=10(米),
在Rt△ABD中,∠ADB=45°,
∴△ABD为等腰直角三角形,
∴BD=AB=30米,
∴CD=BE=AB﹣AE=(30﹣10)米,
即甲楼的高为(30﹣10)米,
故答案为:(30﹣10).
13.
【分析】根据正切的定义分别求出DH、CH,结合图形计算即可.
【解析】连接AD,过点A作AH⊥CD于点H,则四边形ABDH是矩形,
∴AB=DH=m米,
在Rt△ADH中,∠DAH=β,
∴tanβ,
∴AH,
在Rt△ACH中,∠CAH=α,
∴CH=AH tanα tanα(米),
答:两栋教学楼的高度差CH为米.
故答案为:.
14.
【分析】利用解直角三角形的知识知一边和角求另一边即可.
【解析】根据题意得到AB=30米,∠BAC=30°,
∵AB⊥BC,
∴BC=AB tan30°=3010米,
∴标志物C离此栋楼房的地面距离BC为10米,
故答案为10.
15.
【分析】延长CB交水平面于点D,根据题意可得CD⊥AD,再根据坡度可得BD:AD=1:2.4,根据勾股定理可得BD=25,AD=60,最后根据锐角三角函数即可求出CB的长.
【解析】如图,延长CB交水平面于点D,
根据题意可知:
CD⊥AD,
∴∠ADC=90°,
在Rt△ADB中,AB=65,
∵BD:AD=1:2.4,
∴AD=2.4BD,
根据勾股定理,得
AD2+BD2=AB2,
即BD2+(2.4BD)2=652,
解得BD=25,
∴AD=60,
在Rt△ACD中,∠CAD=30°,
∴tan30°,
即,
解得CB=2025(米).
答:树高BC等于(2025)米.
故答案为:(2025).
16.
【分析】过点E作EG⊥AB于G,过点F作FH⊥AB于H,可得四边形ECBG,HBDF是矩形,在Rt△AEG中,根据三角函数求得EG,在Rt△AHP中,根据三角函数求得AH,再根据线段的和差关系即可求解.
【解析】过点E作EG⊥AB于G,过点F作FH⊥AB于H,
则四边形ECBG,HBDF是矩形,
∴EC=GB=20,HB=FD,
∵B为CD的中点,
∴EG=CB=BD=HF,
由已知得:∠EAG=90°﹣60°=30°,∠AFH=45°.
在Rt△AEG中,AG=AB﹣GB=50﹣20=30米,
∴EG=AG tan30°=3010米,
在Rt△AHP中,AH=HF tan45°=10米,
∴FD=HB=AB﹣AH=50﹣10(米).
答:2号楼的高度为(50﹣10)米.
故答案为:(50﹣10).
17.
【分析】易得CD=BD,那么利用30°的正切值即可求得BD长,即为飞机与地面的高度.
【解析】作CD⊥AB于点D.
∴∠BDC=90°,
∵∠DBC=45°,
∴BD=CD,
∵∠DAC=30°,
∴tan30°,
解得CD=BD=500500(米).
答:该飞机与地面的高度是(500500)米.
故答案为:(500500).
18.
【分析】在Rt△ABC中,已知角的邻边求对边,可以用正切求BC,再加上CE即可.
【解析】过A作AC⊥BE于C,
则AC=DE=15,
根据题意:在Rt△ABC中,有BC=AC×tan45°=15,
则BE=BC+CE=16.8(米),
故答案为:16.8.
三、解答题
19.连接AB、AD、AC,过点A作AE⊥BC于E,
则∠AEB=∠AEC=90°,
由题意得:点A、B在圆D上,
∴DB=DA,
在Rt△ABE中,∠BAE=15°,
∴∠DBA=∠DAB=75°,∠DAE=60°,
∵DA=10米,
∴AE=5(米),
∴BE=AE×tan15°≈5×0.27=1.35(米),
∵∠EAC=76°,
∴CE=AE×tan76°≈5×4.01=20.05(米),
∴BC=BE+CE=1.35+20.05≈21(米),
答:摩天轮顶端B与地面的距离约为21米.
20.(1)过点A作AD垂直HB,交HB的延长线于点D,
即∠ADB=90°,
由题意得:i=1:,AB=60(米),
∴,
即;
又∵AB2=AD2+BD2,
即,
∴AD=20(米),
答:山坡的高度为20米;
(2)作AE∥BH交GH于点E,
∵AD⊥BH,GH⊥BH,
∴AD∥GH,
即:四边形ADHE是平行四边形,
由题意可知:∠GAE=30°,BH=60(米),
∵(米),
∴(米),
在Rt△AGE中,,
∴(米),
又∵EH=AD=20(米),
∴(米),
答:铁塔的高度GH为米.
21.(1)根据题意,得∠CAB=37°,CD=220米,∠DAB=30°,∠DBA=45°,
如图,过点C和点D作CE和DF垂直于AB于点E和F,
∵CD∥AB,
∴四边形CDFE是矩形,
∴CE=DF,CD=EF,
∵∠DBA=45°,
∴DF=BF,
设DF=BF=CE=x米,
在Rt△ADF中,∠DAF=30°,DF=x米,
∴AFDFx(米),
∴AE=AF﹣EF=(x﹣220)米,
在Rt△AEC中,∠CAE=37°,
∵CE=AE tan37°,
∴x=(x﹣220)×0.75,
解得x=60(34)=(180240)米,
∴AEx﹣220=(320+240)米,
FB=x=(180240)(米),
∴AB=AE+EF+FB
=320+240220+180240
=780+420
≈1507(米),
答:限速道路AB的长约为1507米;
(2)∵1分20秒小时,
∴该汽车的速度约为:150767.8km/h>60km/h,
∴该车超速.
22.(1)过点B作BE⊥AD于点E,BF⊥CD于点F,
在Rt△ABE中,BE:AE=1:2.4=5:12,
设BE=5xm,AE=12xm,
在Rt△ABE中,由勾股定理得:AB13x(m),
∴13x=26,
解得:x=2(m),
∴BE=FD=5x=10(m),
∴点B到地面的高度为10m;
(2)AE=12x=24(m),
过点B作BF⊥CD于点F,
∵CD⊥AD,
∴四边形BEDF是矩形,
∴DF=BE=10m,BF=DE,
∵tan∠CBF,
∴BFCF=DE,
∵tan∠CAD,
∴,
即:,
解得:CF=8(m),
∴CD=DF+CF=10+8=18(m).
23.∵AC⊥BE,AC⊥CD,AC∥ED,
∴四边形BCDE是矩形,
∴BC=DE,CD=BE=46cm,
由题意可得∠AEB=53°,∠ADC=64°,
在Rt△ABE中,tan53°,
∴AB=BEtan53°,
在Rt△ACD中,tan64°,
∴AC=CDtan64°,
∴ED=BC=AC﹣AB≈46×2.05﹣46×1.33=94.30﹣61.18=33.12≈33(cm),
答:椅脚高ED的长约为33cm.
24.(1)作DH⊥AE于H,如图所示:
在Rt△ADH中,∵,
∴AH=2DH,
∵AH2+DH2=AD2,
∴(2DH)2+DH2=(6)2,
∴DH=6(米).
答:乙同学从点A到点D的过程中,他上升的高度为6米;
(2)如图所示:过点D作DG⊥BC于点G,设BC=x米,
在Rt△ABC中,∠BAC=45°,
∴AC=BC=x,
由(1)得AH=2DH=12,
在矩形DGCH中,DH=CG=6,DG=CH=AH+AC=x+12,
在Rt△BDG中,BG=BC﹣CG=BC﹣DH=x﹣6,
∵tan∠BDG,
∴0.5,
解得:x=24(米),
答:大树的高度约为24米.
