09押浙江卷第23题(二次函数的应用与综合)-2024年浙江省中考数学题号押题(含解析)
文档属性
| 名称 | 09押浙江卷第23题(二次函数的应用与综合)-2024年浙江省中考数学题号押题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 11:05:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
押题方向:二次函数应用及综合问题
2023年浙江真题 考点 命题趋势
2023年湖州卷第21题 二次函数的应用 从近几年浙江各地中考来看,解答题中二次函数考查内容主要是二次函数的实际应用、二次函数综合,其中二次函数的综合题经常以压轴题出现,试题的整体难度比较高,预计2024年浙江卷还将重视二次函数综合问题的考查。
2023年湖州卷、衢州卷、绍兴卷、舟山、嘉兴卷、丽水卷第23题、杭州卷第22题、金华卷第24题 二次函数的综合
1.(2023 杭州)设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
2.(2023 丽水)已知点(﹣m,0)和(3m,0)在二次函数y=ax2+bx+3(a,b是常数,a≠0)的图象上.
(1)当m=﹣1时,求a和b的值;
(2)若二次函数的图象经过点A(n,3)且点A不在坐标轴上,当﹣2<m<﹣1时,求n的取值范围;
3.(2023 宁波)如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).
(1)求该二次函数的表达式及图象的顶点坐标.
(2)当y≤﹣2时,请根据图象直接写出x的取值范围.
4.(2023 绍兴)已知二次函数y=﹣x2+bx+c.
(1)当b=4,c=3时,
①求该函数图象的顶点坐标;
②当﹣1≤x≤3时,求y的取值范围;
(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.
5.(2023 湖州)某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量y(千克)与销售价格x(元/千克)(30≤x<60)存在一次函数关系,部分数据如表所示:
销售价格x(元/千克) 50 40
日销售量y(千克) 100 200
(1)试求出y关于x的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为W元,如果不考虑其他因素,求当销售价格x为多少时,日销售利润W最大?最大的日销售利润是多少元?
6.(2023 温州)一次足球训练中,小明从球门正前方8m的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素);
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25m处?
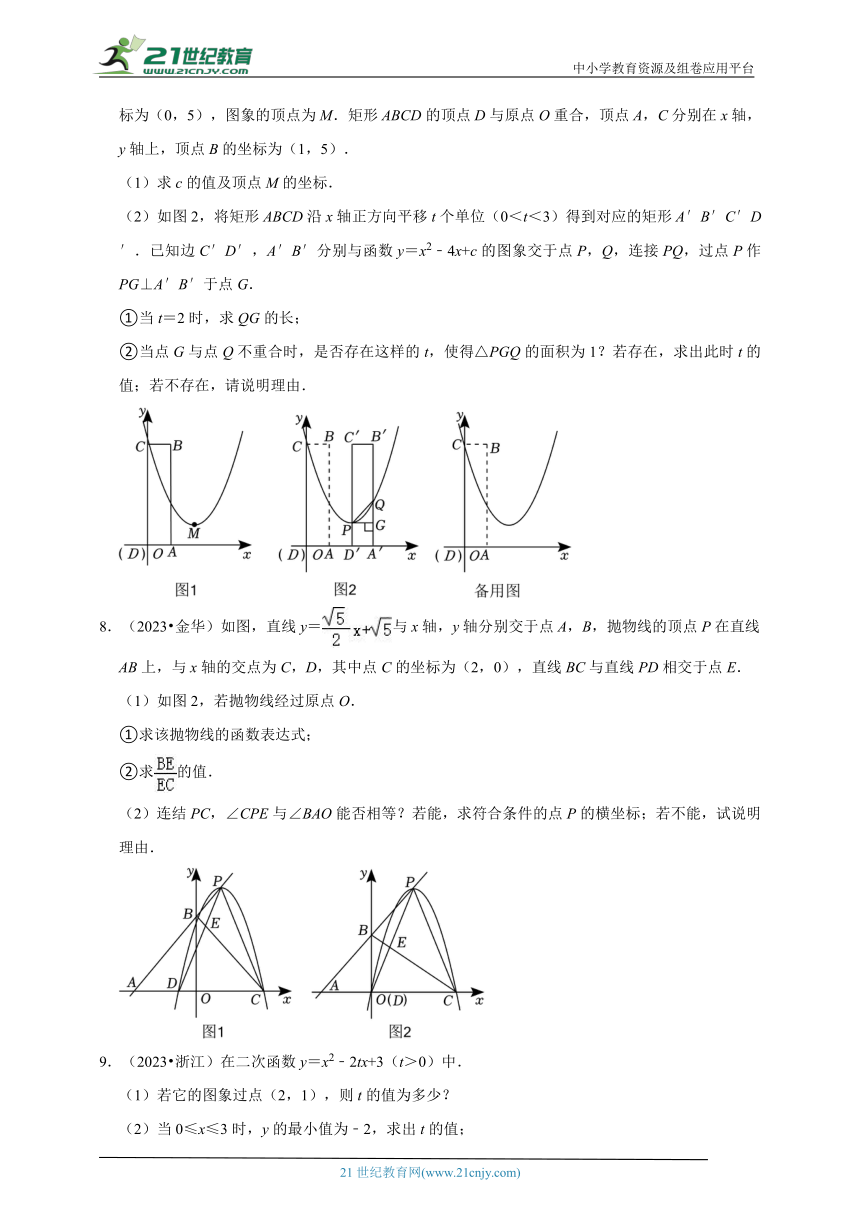
7.(2023 湖州)如图1,在平面直角坐标系xOy中,二次函数y=x2﹣4x+c的图象与y轴的交点坐标为(0,5),图象的顶点为M.矩形ABCD的顶点D与原点O重合,顶点A,C分别在x轴,y轴上,顶点B的坐标为(1,5).
(1)求c的值及顶点M的坐标.
(2)如图2,将矩形ABCD沿x轴正方向平移t个单位(0<t<3)得到对应的矩形A′B′C′D′.已知边C′D′,A′B′分别与函数y=x2﹣4x+c的图象交于点P,Q,连接PQ,过点P作PG⊥A′B′于点G.
①当t=2时,求QG的长;
②当点G与点Q不重合时,是否存在这样的t,使得△PGQ的面积为1?若存在,求出此时t的值;若不存在,请说明理由.
8.(2023 金华)如图,直线y=与x轴,y轴分别交于点A,B,抛物线的顶点P在直线AB上,与x轴的交点为C,D,其中点C的坐标为(2,0),直线BC与直线PD相交于点E.
(1)如图2,若抛物线经过原点O.
①求该抛物线的函数表达式;
②求的值.
(2)连结PC,∠CPE与∠BAO能否相等?若能,求符合条件的点P的横坐标;若不能,试说明理由.
9.(2023 浙江)在二次函数y=x2﹣2tx+3(t>0)中.
(1)若它的图象过点(2,1),则t的值为多少?
(2)当0≤x≤3时,y的最小值为﹣2,求出t的值;
(3)如果A(m﹣2,a),B(4,b),C(m,a)都在这个二次函数的图象上,且a<b<3.求m的取值范围.
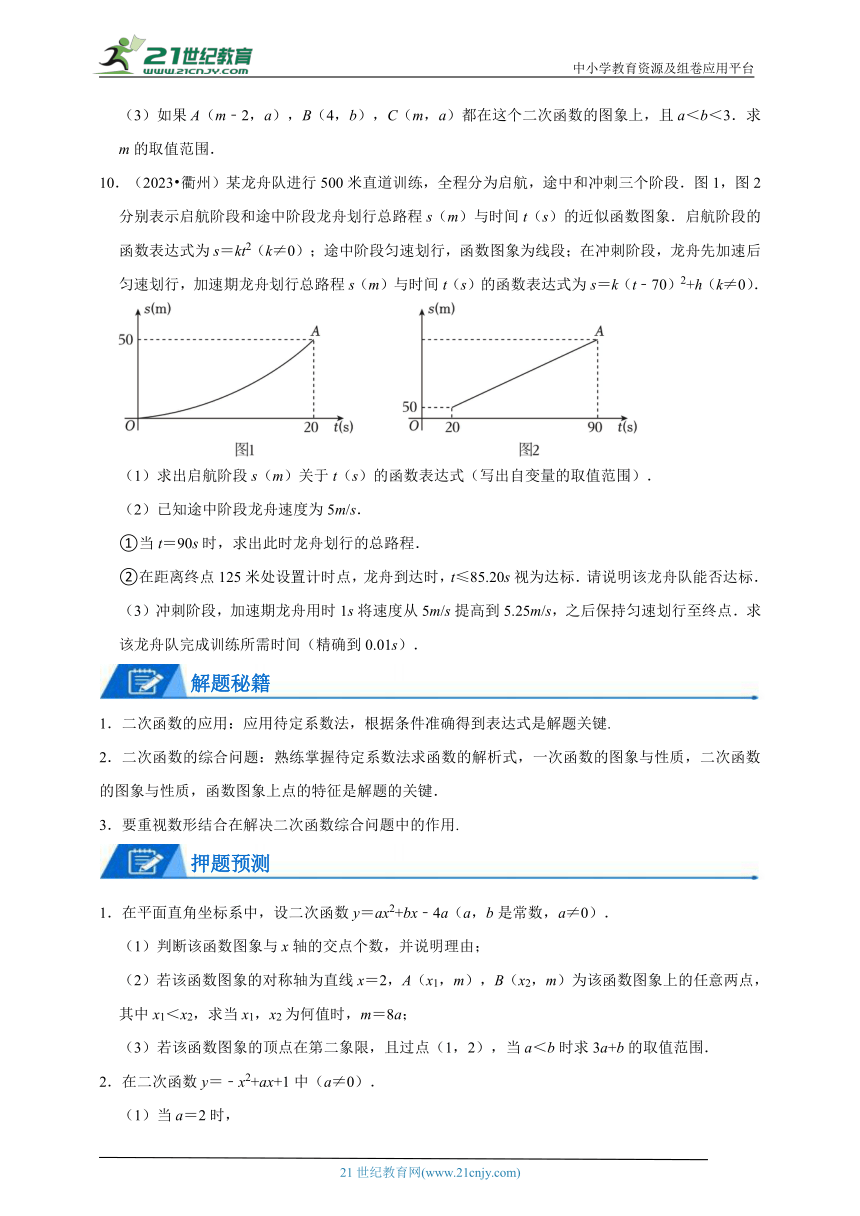
10.(2023 衢州)某龙舟队进行500米直道训练,全程分为启航,途中和冲刺三个阶段.图1,图2分别表示启航阶段和途中阶段龙舟划行总路程s(m)与时间t(s)的近似函数图象.启航阶段的函数表达式为s=kt2(k≠0);途中阶段匀速划行,函数图象为线段;在冲刺阶段,龙舟先加速后匀速划行,加速期龙舟划行总路程s(m)与时间t(s)的函数表达式为s=k(t﹣70)2+h(k≠0).
(1)求出启航阶段s(m)关于t(s)的函数表达式(写出自变量的取值范围).
(2)已知途中阶段龙舟速度为5m/s.
①当t=90s时,求出此时龙舟划行的总路程.
②在距离终点125米处设置计时点,龙舟到达时,t≤85.20s视为达标.请说明该龙舟队能否达标.
(3)冲刺阶段,加速期龙舟用时1s将速度从5m/s提高到5.25m/s,之后保持匀速划行至终点.求该龙舟队完成训练所需时间(精确到0.01s).
1.二次函数的应用:应用待定系数法,根据条件准确得到表达式是解题关键.
2.二次函数的综合问题:熟练掌握待定系数法求函数的解析式,一次函数的图象与性质,二次函数的图象与性质,函数图象上点的特征是解题的关键.
3.要重视数形结合在解决二次函数综合问题中的作用.
1.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
2.在二次函数y=﹣x2+ax+1中(a≠0).
(1)当a=2时,
①求该二次函数图象的顶点坐标;
②当0≤x≤3时,求y的取值范围;
(2)若A(a﹣2,b),B(a,c)两点都在这个二次函数的图象上,且b<c,求a的取值范围.
3.已知二次函数y=x2﹣2kx+k﹣2的图象过点(5,5).
(1)求二次函数的表达式.
(2)若A(x1,y1)和B(x2,y2)都是二次函数图象上的点,且x1+2x2=2,求y1+y2的最小值.
(3)若点P(a,n)和Q(b,n+2)都在二次函数的图象上,且a<b.对于某一个实数n,若b﹣a的最小值为1,则b﹣a的最大值为多少?
4.定义:对于y关于x的函数,函数在x1≤x≤x2(x1<x2)范围内的最大值,记作M[x1,x2].
如函数y=2x,在﹣1≤x≤3范围内,该函数的最大值是6,即M[﹣1,3]=6.
请根据以上信息,完成以下问题:
已知函数y=(a﹣1)x2﹣4x+a2﹣1(a为常数).
(1)若a=2.
①直接写出该函数的表达式,并求M[1,4]的值;
②已知,求p的值.
(2)若该函数的图象经过点(0,0),且M[﹣3,k]=k,求k的值.
5.设二次函数y=ax2+bx+1(a≠0,b是常数),已知函数值y和自变量x的部分对应取值如表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=0时,求二次函数的表达式;
(2)当﹣1≤x≤3时,y有最小值为,求a的值;
(3)若a<﹣3,求证:n﹣m﹣p>20.
6.已知点A(m,p),B(3,q),C(m+2,p)都在二次函数y=2x2+bx+4的图象上.
(1)若m=1,求该二次函数的表达式;
(2)求p+q的最大值;
(3)若p<q<4,求m的取值范围.
7.已知二次函数y1=ax(x+b)(a≠0)和一次函数y2=ax+m.
(1)若二次函数y1的图象过点(1,0)和(2,2),求二次函数的表达式.
(2)若一次函数y2与二次函数y1的图象交于x轴上同一点A,且A不是原点.
①求证:m=ab;
②若二次函数y1与一次函数y2的另一个交点B为y1的顶点,求b的值.
8.设一次函数y1=a(x+m)的图象与x轴交于点A,二次函数的图象与x轴交于A,B两个不同的点,设函数y=y1+y2.
(1)设点Q(0,q)在函数y的图象上,若q>c,求证:am>0.
(2)若函数y2,y的图象在x轴上截得的线段长分别为d1,d2,求d1,d2的数量关系式.
(3)若函数y1的图象分别与函数y2的图象、函数y的图象交于点E(x1,e),F(x2,f),且点E,F不同于点A,求x1﹣x2的值.
9.如图,小车从点A出发,沿与水平面成30°角光滑斜坡AB下滑,在下滑过程中小车速度逐渐增加,设小车出发点A离水平地面BE的高度为h,小车从点A滑行到最低点B所用的时间为t(秒),小车滑行到点B时的速度为v(厘米/秒).速度v与时间t满足关系:v=10t,高度h与时间t满足关系:(g≠0,g是常数),当小车出发点小车出发点A离水平地面BE的高度为20(厘米)时,小车从点A滑到最低点B需要2秒.
(1)当小车出发点A离水平地面BE的高度为45(厘米)时,小车滑到最低点B需要几秒钟?此时小车到达B点时的速度是多少?
(2)小车继续在粗糙的水平地面BE上滑行,设滑行的距离为s(厘米),小车从斜坡滑行到点B时速度为v(厘米/秒),小车在水平地面BE上滑行的时间为T(秒),若s与v,T之间满足以下关系:+vT(a≠0,a是常数),当v=20(厘米/秒)时,s=50(厘米),T=5(秒).如果把小车出发点A离水平地面BE的距离h提高到125厘米,那么当滑行到时间T=4秒时,小车在水平地面BE上滑行的距离为多少?
10.周末,小明和同学们一起去长江路地铁站坐地铁.在等车的过程中,他惊叹于地铁每次都能精准的停靠在停止线上.为什么每次地铁停靠都那么准呢?里面一定包含着数学知识!通过工作人员帮助,小明获得了地铁刹车开始的时间t与地铁到停止线的距离S之间的表格信息:
t(秒) 0 4 8 12 16 20 24 …
S(米) 256 196 144 100 64 36 16 …
当小明拿到这些数据时,他作了如下的思考:
(1)依据数学经验,小明需要将这些数据绘制在平面直角坐标系中,并用平滑的曲线进行连线,形成数据所生成的图象,请你在图中落实他的想法;
(2)根据图象以及数据关系,它可能是我们所学习过的 二次 函数图象(选填“一次”、“二次”或“反比例”).请你选择合适的数据求出该函数的表达式;
(3)地铁从开始刹车到下次启动一共用时60秒.求地铁的停靠时间.
(停靠时间指的是地铁刹停后的静止时间)
11.已知二次函数y=ax2+bx+c(a≠0),且a>b>c,a+b+c=0.
(1)当b=0时,求方程ax2+bx+c=0的根;
(2)已知该二次函数的对称轴为x=m,求证:;
(3)已知该二次函数的图象与x轴,y轴分别交于A(x1,0),B(x2,0),C(0,c)三点(A在B的左侧),且x1+4x2=0,若△ABC为直角三角形,求该二次函数表达式.
11.某个农场有一个花卉大棚,是利用部分墙体建造的.其横截面顶部为抛物线型,大棚的一端固定在墙体OA上,另一端固定在墙体BC上,其横截面有2根支架DE,FG,相关数据如图1所示,其中支架DE=BC,OF=DF=BD,这个大棚用了400根支架.
为增加棚内空间,农场决定将图1中棚顶向上调整,支架总数不变,对应支架的长度变化,如图2所示,调整后C与E上升相同的高度,增加的支架单价为60元/米(接口忽略不计),需要增加的经费不超过32000元.
(1)分别以OB和OA所在的直线为x轴和y轴建立平面直角坐标系.
①求出改造前的函数解析式.
②当CC′=1米,求GG′的长度.
(2)只考虑经费情况下,求出CC′的最大值.
12.根据以下素材,探索完成任务.
设计跳长绳方案
素材1:某校组织跳长绳比赛,要求如下:(1)每班需要报名跳绳同学9人,摇绳同学2人;(2)跳绳同学需站成一路纵队,原地起跳,如图1.
素材2:某班进行赛前训练,发现:(1)当绳子摇至最高处或最低处时,可近似看作两条对称分布的抛物线,已知摇绳同学之间水平距离为6m,绳子最高点为2m,摇绳同学的出手高度均为1m,如图2;(2)9名跳绳同学身高如右表. 身高(m)1.701.731.751.80人数2241
素材3:观察跳绳同学的姿态(如图3),发现:(1)跳绳时,人的跳起高度在0.25m及以下较为舒适;(2)当长绳摇至最高处时,人正屈膝落地,此时头顶到地面的高度是身高的.
问题解决
任务1:确定长绳形状.请在图2中以长绳触地点为原点建立直角坐标系,并求出长绳摇至最高处时,对应抛物线的解析式.
任务2:确定排列方案.该班班长决定:以长绳的触地点为中心,将同学按“中间高,两边低”的方式对称排列,同时保持0.45m的间距.请计算当绳子在最高点时,长绳是否会触碰到最边侧的同学.
任务3:方案优化改进.据最边侧同学反映:由于跳起高度过高,导致不舒适,希望作出调整.班长给出如下方案:摇绳同学在绳即将触地时,将出手高度降低至0.85m.此时中段长绳将贴地形成一条线段(x线段AB),而剩余的长绳则保持形状不变,如图4.请你通过计算说明,该方案是否可解决同学反映的问题.
13.
设计喷水方案
素材1 图1为某公园的圆形喷水池,图2是其示意图,O为水池中心,喷头A、B之间的距离为20米,喷射水柱呈抛物线形,水柱距水池中心7m处达到最高,高度为5m,水池中心处有一个圆柱形蓄水池,其底面直径CD为12m,高CF为1.8米
素材2 如图3、图4,拟将在圆柱形蓄水池中心处建一能伸缩高度的喷水装置OP(OP⊥CD),要求水柱不能碰到图2中的水柱,也不能落在蓄水池外面.经调研,目前市场有两种喷水头均能喷射与图2中形状相同的抛物线.其中,甲喷水头以点P为最高点向四周喷射水柱(如图3),乙喷水头喷射水柱的最高点与点P的高度差为0.8m(如图4).
问题解决
任务1 确定水柱形状 在图2中以点O为坐标原点,水平方向为轴建立直角坐标系,求左边这条抛物线的函数表达式.
任务2 选择喷水装置甲,确定喷水装置的最高高度 若选择甲装置(图3),为防止水花溅出,当落水点G、M之间的距离满足时,OP不能再升高,求此时OP的最高高度.
任务3 选择喷水装置乙,拟定喷水装置的高度范围 若选择乙装置(图4),为了美观,要求OP喷出的水柱高度不低于5m,求喷水装置OP高度的变化范围.
14.在平面直角坐标系中,点(1,m)和(3,n)都在二次函数y=ax2+bx(a≠0,a,b是常数)的图象上.
(1)若m=n=﹣6,求该二次函数的表达式和函数图象的对称轴.
(2)若a=﹣1,m<n,求b的取值范围.
(3)已知点(﹣1,y1),(2,y2),(4,y3)也都在该二次函数图象上,若mn<0且a<0,试比较y1,y2,y3的大小,并说明理由.
15.如图,二次函数y=ax2+bx+3(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,C为顶点.
(1)请求出二次函数的表达式及图象的顶点C的坐标.
(2)若点E为抛物线对称轴左侧一点,过点E作x轴平行线交对称轴于点D,若ED=m,试用m的代数式表示CD.
(3)连结EC,过点C作CF⊥EC交抛物线于点F,过点F作x轴的平行线交对称轴于点G,证明:GF DE=1.
16.已知二次函数的图象经过原点O和点A(8+t,0),其中t≥0.
(1)当t=0时.
①求y关于x的函数表达式,并求出当x为何值时,y有最大值,最大值为多少?
②当x=m和x=n时(m≠n),函数值相等,求m,n之间的关系式.
(2)当t>0时,在0≤x≤8范围内,y是否存在最大值18?若存在,求出相应的t和x的值,若不存在,请说明理由.
答案与解析
押题方向:二次函数应用及综合问题
2023年浙江真题 考点 命题趋势
2023年湖州卷第21题 二次函数的应用 从近几年浙江各地中考来看,解答题中二次函数考查内容主要是二次函数的实际应用、二次函数综合,其中二次函数的综合题经常以压轴题出现,试题的整体难度比较高,预计2024年浙江卷还将重视二次函数综合问题的考查。
2023年湖州卷、衢州卷、绍兴卷、舟山、嘉兴卷、丽水卷第23题、杭州卷第22题、金华卷第24题 二次函数的综合
1.(2023 杭州)设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
【点拨】(1)①利用待定系数法即可求得;
②利用二次函数的性质得出结论;
(2)根据题意m≤0,由﹣=1,得出b=﹣2a,则二次函数为y=ax2﹣2ax+1,得出m=a+2a+1≤0,解得a≤﹣.
【解析】解:(1)①由题意得,
解得,
∴二次函数的表达式是y=x2﹣2x+1;
②∵y=x2﹣2x+1=(x﹣1)2,
∴抛物线开口向上,对称轴为直线x=1,
∴当x<1时,y随x的增大而减小;
(2)∵x=0和x=2时的函数值都是1,
∴抛物线的对称轴为直线x=﹣=1,
∴(1,n)是顶点,(﹣1,m)和(3,p)关于对称轴对称,
若在m,n,p这三个实数中,只有一个是正数,则抛物线必须开口向下,且m≤0,
∵﹣=1,
∴b=﹣2a,
∴二次函数为y=ax2﹣2ax+1,
∴m=a+2a+1≤0,
∴a≤﹣.
【点睛】本题考查了二次函数的图象与系数的关系,待定系数法求二次函数的解析式,二次函数的性质,二次函数图象上点的坐标特征,能够明确题意得出m=a+2a+1<0是解题的关键.
2.(2023 丽水)已知点(﹣m,0)和(3m,0)在二次函数y=ax2+bx+3(a,b是常数,a≠0)的图象上.
(1)当m=﹣1时,求a和b的值;
(2)若二次函数的图象经过点A(n,3)且点A不在坐标轴上,当﹣2<m<﹣1时,求n的取值范围;
【点拨】(1)当m=﹣1时,二次函数y=ax2+bx+3图象过点(1,0)和(﹣3,0),用待定系数法可得a的值是﹣1,b的值是﹣2;
(2)y=ax2+bx+3图象过点(﹣m,0)和(3m,0),可知抛物线的对称轴为直线x=m,而y=ax2+bx+3的图象过点A(n,3),(0,3),且点A不在坐标轴上,可得m=,根据﹣2<m<﹣1,即得﹣4<n<﹣2;
(3)由抛物线过(﹣m,0),(3m,0),可得﹣=m,b=﹣2am,把 (﹣m,0),(3m,0)代入y=ax2+bx+3变形可得am2+1=0,故b2+4a=(﹣2am)2+4a=4a(am2+1)=4a×0=0.
【解析】(1)解:当m=﹣1时,二次函数y=ax2+bx+3图象过点(1,0)和(﹣3,0),
∴,
∴解得,
∴a的值是﹣1,b的值是﹣2;
(2)解:∵y=ax2+bx+3图象过点(﹣m,0)和(3m,0),
∴抛物线的对称轴为直线x=m,
∵y=ax2+bx+3的图象过点A(n,3),(0,3),且点A不在坐标轴上,
∴由图象的对称性得n=2m,
∴m=,
∵﹣2<m<﹣1,
∴﹣2<<﹣1,
∴﹣4<n<﹣2;
(3)证明:∵抛物线过(﹣m,0),(3m,0),
∴抛物线对称轴为直线x==m,
∴﹣=m,
∴b=﹣2am,
把(﹣m,0),(3m,0)代入y=ax2+bx+3得:
,
①×3+②得:12am2+12=0,
∴am2+1=0,
∴b2+4a=(﹣2am)2+4a=4a(am2+1)=4a×0=0.
【点睛】本题考查二次函数图象上点坐标的特征,涉及待定系数法,不等式,方程组等知识,解题的关键是整体思想的应用.
3.(2023 宁波)如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).
(1)求该二次函数的表达式及图象的顶点坐标.
(2)当y≤﹣2时,请根据图象直接写出x的取值范围.
【点拨】(1)用待定系数法求出函数表达式,配成顶点式即可得顶点坐标;
(2)求出A关于对称轴的对称点坐标,由图象直接可得答案.
【解析】解:(1)把A(1,﹣2)和B(0,﹣5)代入y=x2+bx+c得:
,
解得,
∴二次函数的表达式为y=x2+2x﹣5,
∵y=x2+2x﹣5=(x+1)2﹣6,
∴顶点坐标为(﹣1,﹣6);
(2)如图:
∵点A(1,﹣2)关于对称轴直线x=﹣1的对称点C(﹣3,﹣2),
∴当y≤﹣2时,x的范围是﹣3≤x≤1.
【点睛】本题考查二次函数图象及性质,解题的关键是掌握待定系数法,求出函数表达式.
4.(2023 绍兴)已知二次函数y=﹣x2+bx+c.
(1)当b=4,c=3时,
①求该函数图象的顶点坐标;
②当﹣1≤x≤3时,求y的取值范围;
(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.
【点拨】(1)先把解析式进行配方,再求顶点;
(2)根据函数的增减性求解;
(3)根据函数的图象和系数的关系,结合图象求解.
【解析】解:(1)①∵b=4,c=3 时,
∴y=﹣x2+4x+3=﹣(x﹣2)2+7,
∴顶点坐标为(2,7).
②∵﹣1≤x≤3中含有顶点(2,7),
∴当 x=2 时,y有最大值7,
∵2﹣(﹣1)>3﹣2,
∴当x=﹣1 时,y有最小值为:﹣2,
∴当﹣1≤x≤3时,﹣2≤y≤7.
(2)∵x≤0时,y的最大值为2;x>0时,y的最大值为3,
∴抛物线的对称轴 在y轴的右侧,
∴b>0,
∵抛物线开口向下,x≤0时,y的最大值为2,
∴c=2,
又∵,
∴b=±2,
∵b>0,
∴b=2.
∴二次函数的表达式为 y=﹣x2+2x+2.
【点睛】本题考查了二次函数的性质,掌握数形结合思想是解题的关键.
5.(2023 湖州)某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量y(千克)与销售价格x(元/千克)(30≤x<60)存在一次函数关系,部分数据如表所示:
销售价格x(元/千克) 50 40
日销售量y(千克) 100 200
(1)试求出y关于x的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为W元,如果不考虑其他因素,求当销售价格x为多少时,日销售利润W最大?最大的日销售利润是多少元?
【点拨】(1)设y与x之间的函数关系式为y=kx+b,由表中数据即可得出结论;
(2)根据每日总利润=每千克利润×销售量列出函数解析式,根据函数的性质求最值即可.
【解析】解:(1)设y关于x的函数表达式为y=kx+b(k≠0).
将x=50,y=100和x=40,y=200分别代入,得:,
解得:,
∴y关于x的函数表达式是:y=﹣10x+600.
(2)W=(x﹣30)(﹣10x+600)=﹣10x2+900x﹣18000.
当x=﹣=45时,在30≤x<60的范围内,W取到最大值,最大值是2250.
答:销售价格为每千克45元时,日销售利润最大,最大日销售利润是2250元.
【点睛】本题考查一次函数、二次函数的应用,关键是根据等量关系写出函数解析式.
6.(2023 温州)一次足球训练中,小明从球门正前方8m的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素);
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25m处?
【点拨】(1)求出抛物线的顶点坐标为(2,3),设抛物线为 y=a(x﹣2)2+3,用待定系数法可得y=﹣(x﹣2)2+3;当x=0时,y=﹣×4+3=>2.44,知球不能射进球门.
(2)设小明带球向正后方移动m米,则移动后的抛物线为y=﹣(x﹣2﹣m)2+3,把点(0,2.25)代入得 m=﹣5(舍去)或m=1,即知当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方2.25m处.
【解析】解:(1)∵8﹣6=2,
∴抛物线的顶点坐标为(2,3),
设抛物线为 y=a(x﹣2)2+3,
把点A(8,0)代入得:36a+3=0,
解得a=﹣,
∴抛物线的函数表达式为y=﹣(x﹣2)2+3;
当x=0时,y=﹣×4+3=>2.44,
∴球不能射进球门.
(2)设小明带球向正后方移动m米,则移动后的抛物线为y=﹣(x﹣2﹣m)2+3,
把点(0,2.25)代入得:2.25=﹣(0﹣2﹣m)2+3,
解得 m=﹣5(舍去)或m=1,
∴当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方2.25m处.
【点睛】本题考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
7.(2023 湖州)如图1,在平面直角坐标系xOy中,二次函数y=x2﹣4x+c的图象与y轴的交点坐标为(0,5),图象的顶点为M.矩形ABCD的顶点D与原点O重合,顶点A,C分别在x轴,y轴上,顶点B的坐标为(1,5).
(1)求c的值及顶点M的坐标.
(2)如图2,将矩形ABCD沿x轴正方向平移t个单位(0<t<3)得到对应的矩形A′B′C′D′.已知边C′D′,A′B′分别与函数y=x2﹣4x+c的图象交于点P,Q,连接PQ,过点P作PG⊥A′B′于点G.
①当t=2时,求QG的长;
②当点G与点Q不重合时,是否存在这样的t,使得△PGQ的面积为1?若存在,求出此时t的值;若不存在,请说明理由.
【点拨】(1)运用待定系数法将(0,5)代入y=x2﹣4x+c,即可求得c的值,再利用配方法将抛物线的解析式化为顶点式或运用顶点公式即可求得答案;
(2)①当t=2时,D′,A′的坐标分别是(2,0),(3,0).进而可求得点P、Q的纵坐标,利用QG=yQ﹣yG,即可求得答案;
②根据题意,得:P(t,t2﹣4t+5),Q(t+1,t2﹣2t+2),G(t+1,t2﹣4t+5),分两种情况:当点G在点Q的上方时,当点G在点Q的下方时,分别求得t的值即可.
【解析】解 (1)∵二次函数y=x2﹣4x+c的图象与y轴的交点坐标为(0,5),
∴c=5,
∴y=x2﹣4x+5=(x﹣2)2+1,
∴顶点M的坐标是(2,1).
(2)①如图1,∵A在x轴上,B的坐标为(1,5),
∴点A的坐标是(1,0).
当t=2时,D′,A′的坐标分别是(2,0),(3,0).
当x=3时,y=32﹣4×3+5=2,即点Q的纵坐标是2.
当x=2时,y=1,即点P的纵坐标是1.
∵PG⊥A′B′,
∴点G的纵坐标是1,
∴QG=2﹣1=1.
②存在.理由如下:
∵△PGQ的面积为1,PG=1,
∴QG=2.
根据题意,得:P(t,t2﹣4t+5),Q(t+1,t2﹣2t+2),
∴G(t+1,t2﹣4t+5),
如图2,当点G在点Q的上方时,
QG=t2﹣4t+5﹣(t2﹣2t+2)=3﹣2t=2,
此时(在0<t<3的范围内).
如图3,当点G在点Q的下方时,
QG=t2﹣2t+2﹣(t2﹣4t+5)=2t﹣3=2,
此时(在0<t<3的范围内).
综上所述,存在t,使得△PGQ的面积为1,此时t的值为或.
【点睛】本题是二次函数综合题,考查了待定系数法,抛物线的顶点,平移变换的性质,三角形面积等,运用数形结合思想和分类讨论思想是解题关键.
8.(2023 金华)如图,直线y=与x轴,y轴分别交于点A,B,抛物线的顶点P在直线AB上,与x轴的交点为C,D,其中点C的坐标为(2,0),直线BC与直线PD相交于点E.
(1)如图2,若抛物线经过原点O.
①求该抛物线的函数表达式;
②求的值.
(2)连结PC,∠CPE与∠BAO能否相等?若能,求符合条件的点P的横坐标;若不能,试说明理由.
【点拨】(1)①由抛物线经过原点O(0,0)、C(2,0),可得抛物线的顶点P(1,),利用待定系数法可得抛物线的函数表达式为y=﹣x2+3x;
②先求出A(﹣2,0),B(0,),运用待定系数法可得直线OP的解析式为y=x,过点B作BF∥x轴交OP于点F,F(,),可得BF=,再由BF∥OC,得出△BEF∽△CEO,进而可得===;
(2)分四种情形,分别作出图形求解即可.
【解析】解:(1)①∵抛物线经过原点O(0,0)、C(2,0),
∴对称轴为直线x=1,
当x=1时,y=×1+=,
∴抛物线的顶点P(1,),
设抛物线的解析式为y=a(x﹣1)2+,把C(2,0)代入,得a+=0,
解得:a=﹣,
∴y=﹣(x﹣1)2+=﹣x2+3x,
∴该抛物线的函数表达式为y=﹣x2+3x;
②∵直线y=与x轴,y轴分别交于点A,B,
∴A(﹣2,0),B(0,),
设直线OP的解析式为y=kx,把P(1,)代入,得:k=,
∴直线OP的解析式为y=x,
如图,过点B作BF∥x轴交OP于点F,则点F的纵坐标与点B的纵坐标相同,
∴=x,
解得:x=,
∴F(,),
∴BF=,
∵BF∥OC,
∴△BEF∽△CEO,
∴===,
∴的值为.
(2)设点P的横坐标为t,
①如图2﹣1,当t>2,存在∠CPE=∠BAO,
设∠CPE=∠BAO=α,∠APC=β,则∠APD=α+β,
∵∠PCD=∠PAO+∠APC=α+β,
∵PC=PD,
∴∠PDC=∠PCD=∠APD,
∴AP=AD=2t,
过点P作PF⊥x轴于点F,则AF=t+2,
在Rt△APF中,cos∠BAO==,
∴=,
∴t=6.
②如图2﹣2中,当0<t≤2时,存在∠CPE=∠BAO.
过点P作PF⊥x轴于点F,
同法cos∠BAO==,
∴=,
∴t=.
③如图2﹣3中,当﹣2<t≤0时,存在∠CPE=∠BAO=α,
∵PC=PD,
∴∠CPE=α,
∴∠BAO﹣∠PDC=α,
∴∠APD=∠PDA,
∴AD=AP=﹣2t,
同法cos∠BAO==,
∴=,
∴t=﹣.
④当t≤﹣2时,同法cos∠BAO==,
=,
∴t=﹣
综上所述.点P的横坐标为6或﹣或或﹣.
【点睛】本题是二次函数综合题,考查了待定系数法求函数解析式,一次函数与二次函数综合运用,勾股定理,等腰三角形性质,相似三角形的判定和性质等,添加辅助线构造相似三角形是解题关键.
9.(2023 浙江)在二次函数y=x2﹣2tx+3(t>0)中.
(1)若它的图象过点(2,1),则t的值为多少?
(2)当0≤x≤3时,y的最小值为﹣2,求出t的值;
(3)如果A(m﹣2,a),B(4,b),C(m,a)都在这个二次函数的图象上,且a<b<3.求m的取值范围.
【点拨】(1)将(2,1)代入y=x2﹣2tx+3即可得t=;
(2)抛物线y=x2﹣2tx+3对称轴为 x=t.若0<t≤3,有t2﹣2t2+3=﹣2,若t>3,有9﹣6t+3=﹣2,解方程并检验可得t的值为;
(3)根据A(m﹣2,a),C(m,a)都在这个二次函数的图象上,可得二次函数y=x2﹣2tx+3的对称轴直线x=t即为直线x==m﹣1,由t>0,得m>1,因m﹣2<m,知A在对称轴左侧,C在对称轴右侧,抛物线y=x2﹣2tx+3与y轴交点为(0,3),其关于对称轴直线x=m﹣1的对称点为(2m﹣2,3),由b<3,知4<2m﹣2,m>3;①当A(m﹣2,a),B(4,b)都在对称轴左侧时,y随x的增大而减小,有4<m﹣2,可得m满足的条件为m>6;②当A(m﹣2,a)在对称轴左侧,B(4,b)在对称轴右侧时,B(4,b)到对称轴直线x=m﹣1距离大于A(m﹣2,a)到对称轴直线x=m﹣1的距离,故4﹣(m﹣1)>m﹣1﹣(m﹣2),得:m<4,m满足的条件是3<m<4.
【解析】解:(1)将(2,1)代入y=x2﹣2tx+3得:
1=4﹣4t+3,
解得:t=;
(2)抛物线y=x2﹣2tx+3对称轴为 x=t.
若0<t≤3,当x=t时函数取最小值,
∴t2﹣2t2+3=﹣2,
解得t=;
若t>3,当x=3时函数取最小值,
∴9﹣6t+3=﹣2,
解得 (不符合题意,舍去);
综上所述,t的值为;
(3)∵A(m﹣2,a),C(m,a)都在这个二次函数的图象上,
∴二次函数y=x2﹣2tx+3的对称轴直线x=t即为直线x==m﹣1,
∴t=m﹣1,
∵t>0,
∴m﹣1>0,
解得m>1,
∵m﹣2<m,
∴A在对称轴左侧,C在对称轴右侧,
在y=x2﹣2tx+3中,令x=0得y=3,
∴抛物线y=x2﹣2tx+3与y轴交点为(0,3),
∴(0,3)关于对称轴直线x=m﹣1的对称点为(2m﹣2,3),
∵b<3,
∴4<2m﹣2,
解得m>3;
①当A(m﹣2,a),B(4,b)都在对称轴左侧时,
∵y随x的增大而减小,且a<b,
∴4<m﹣2,
解得m>6,
此时m满足的条件为m>6;
②当A(m﹣2,a)在对称轴左侧,B(4,b)在对称轴右侧时,
∵a<b,
∴B(4,b)到对称轴直线x=m﹣1距离大于A(m﹣2,a)到对称轴直线x=m﹣1的距离,
∴4﹣(m﹣1)>m﹣1﹣(m﹣2),
解得:m<4,
此时m满足的条件是3<m<4,
综上所述,3<m<4或m>6.
【点睛】本题考查二次函数的综合应用,涉及函数图象上点坐标的特征,解题的关键是分类讨论思想的应用.
10.(2023 衢州)某龙舟队进行500米直道训练,全程分为启航,途中和冲刺三个阶段.图1,图2分别表示启航阶段和途中阶段龙舟划行总路程s(m)与时间t(s)的近似函数图象.启航阶段的函数表达式为s=kt2(k≠0);途中阶段匀速划行,函数图象为线段;在冲刺阶段,龙舟先加速后匀速划行,加速期龙舟划行总路程s(m)与时间t(s)的函数表达式为s=k(t﹣70)2+h(k≠0).
(1)求出启航阶段s(m)关于t(s)的函数表达式(写出自变量的取值范围).
(2)已知途中阶段龙舟速度为5m/s.
①当t=90s时,求出此时龙舟划行的总路程.
②在距离终点125米处设置计时点,龙舟到达时,t≤85.20s视为达标.请说明该龙舟队能否达标.
(3)冲刺阶段,加速期龙舟用时1s将速度从5m/s提高到5.25m/s,之后保持匀速划行至终点.求该龙舟队完成训练所需时间(精确到0.01s).
【点拨】(1)把A(20,50)代入s=kt2 得出k的值,则可得出答案;
(2)①设s=5t+b,把(20,50)代入,得出50=5×20+b,求得b=﹣50,当t=90时,求出s=400,则可得出答案;
②把s=375代入s=5t﹣50,求得t=85,则可得出答案;
(3)由(1)可知k=,把(90,400)代入s=,求得h=350.求出s=405.125,则可得出答案.
【解析】解:(1)把A(20,50)代入s=kt2 得50=400k,
解得,
∴启航阶段总路程s关于时间t的函数表达式为s=(0<t≤20);
(2)①设s=5t+b,把(20,50)代入,得50=5×20+b,
解得b=﹣50,
∴s=5t﹣50.
当t=90时,s=450﹣50=400.
∴当t=90s时,龙舟划行的总路程为400m.
②500﹣125=375,
把s=375代入s=5t﹣50,
得t=85.
∵85<85.20,
∴该龙舟队能达标.
(3)加速期:由(1)可知k=,
把(90,400)代入s=,
得h=350.
∴函数表达式为s=,
把t=91代入s=,
解得s=405.125.
∴(500﹣405.125)÷5.25≈18.07(s),
∴90+1+18.07=109.07(s).
答:该龙舟队完成训练所需时间为109,07s.
【点睛】本题是二次函数综合题,考查了二次函数的应用,一次函数的性质,二次函数图象上点的坐标特征,待定系数法,根据条件准确得到表达式是解题关键.
11.(2024 嘉善县一模)已知二次函数y=ax2+bx+c(a≠0),且a>b>c,a+b+c=0.
(1)当b=0时,求方程ax2+bx+c=0的根;
(2)已知该二次函数的对称轴为x=m,求证:;
(3)已知该二次函数的图象与x轴,y轴分别交于A(x1,0),B(x2,0),C(0,c)三点(A在B的左侧),且x1+4x2=0,若△ABC为直角三角形,求该二次函数表达式.
【点拨】(1)当b=0时,方程为:ax2+c=0,即可求解;
(2)证明a>0且c<0,即可求解;
(3)若△ABC为直角三角形,则只存在∠ACB为直角,即可求解.
【解析】(1)解:∵a>b>c,a+b+c=0,
则a>0且c<0,
当b=0时,方程为:ax2+c=0,
解得:x=±;
(2)证明:由(1)知,a>0且c<0,
则a+b=﹣c>0,
即a+b>0,
则﹣<1,
即﹣<,
∴;
(3)解:∵a>0且c<0,且x1+4x2=0,
解:由(1)知,抛物线的表达式为:y=ax2+bx+(﹣a﹣b),
则x1+x2=﹣且x1x2=﹣,
将x1+4x2=0代入上式两式得:4x2==1+=1+3x2,
解得:x2=1,则x1=﹣4,
即点A、B的坐标分别为:(﹣4,0)、(1,0),
则可大致画出函数的图象如下:
若△ABC为直角三角形,
则只存在∠ACB为直角,
则∵∠ACO+∠OCB=90°,∠OCB+∠OBC=90°,
∴∠ACO=∠OBC,
∴tan∠ACO=tan∠OBC,
则OC2=OA×OB,
即CO2=1×4=4,
解得:CO=2,
则点C(0,﹣2),
由题意得,抛物线的表达式为:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),
则﹣4a=﹣2,
解得:a=,
则抛物线的表达式为:y=x2﹣x﹣2.
【点睛】本题考查的是二次函数综合运用,涉及到解直角三角形、直角三角形的性质等熟悉二次函数的图象和性质是解题的关键.
1.二次函数的应用:应用待定系数法,根据条件准确得到表达式是解题关键.
2.二次函数的综合问题:熟练掌握待定系数法求函数的解析式,一次函数的图象与性质,二次函数的图象与性质,函数图象上点的特征是解题的关键.
3.要重视数形结合在解决二次函数综合问题中的作用.
1.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
【点拨】(1)依据题意,求出Δ=b2﹣4a(﹣4a)=b2+16a2,进而结合a≠0可以判断Δ>0,即可求解;
(2)依据题意,也有对称轴为直线x=2,可得b=﹣4a,从而y=ax2+bx﹣4a=ax2﹣4ax﹣4a,当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,然后计算即可求解;
(3)依据题意,由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,则抛物线开口向下,即a<0,进而求解.
【解析】解:(1)由题意得,Δ=b2﹣4a(﹣4a)=b2+16a2,
又a≠0,
∴a2>0.
∴16a2>0.
又对于任意的b都有b2≥0,
∴Δ=b2+16a2>0.
∴函数图象与x轴的交点个数为2.
(2)∵x=2=﹣,
∴b=﹣4a.
∴抛物线表达式为y=ax2+bx﹣4a=ax2﹣4ax﹣4a,
当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,
解得x=6或﹣2,
则x1=﹣2,x2=6.
(3)将(1,2)代入抛物线表达式得:2=a+b﹣4a,则b=3a+2,
∵a<b,故a<3a+2,
∴解得a>﹣1.
∴抛物线的表达式为y=ax2+(3a+2)x﹣4a,
由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,
∴抛物线开口向下,即a<0.
∴函数的对称轴x=﹣=﹣﹣<0,
解得a<﹣,
∴﹣1<a<﹣.
∴﹣3<3a<﹣2.
故﹣1<3a+2<0,即﹣1<b<0.
∴﹣4<3a+b<﹣2.
∴3a+b的取值范围:﹣4<3a+b<﹣2.
【点睛】本题主要考查的是抛物线与x轴的交点、函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.
2.在二次函数y=﹣x2+ax+1中(a≠0).
(1)当a=2时,
①求该二次函数图象的顶点坐标;
②当0≤x≤3时,求y的取值范围;
(2)若A(a﹣2,b),B(a,c)两点都在这个二次函数的图象上,且b<c,求a的取值范围.
【点拨】(1)①把解析式化成顶点式即可求得;
②根据二次函数的性质,可以得到当0<x<3时,y的取值范围;
(2)根据抛物线的对称性及增减性即可解决问题.
【解析】解:(1)①把 a=2 代入得 y=﹣x2+2x+1=﹣(x﹣1)2+2,
∴抛物线的顶点坐标为(1,2);
②∵y=﹣x2+2x+1的开口向下,对称轴为直线x=1,
∴当0≤x≤1时,y随x的增大而增大,当1≤x≤3时,y随x的增大而减小,
∴当x=1时,y有最大值2.
∵当x=0时,y=1;当x=3时,y=﹣2
∴当0≤x≤3时,﹣2≤y≤2;
(2)抛物线的对称轴为直线 ,
①当 ,即0≤a≤4时,点B到对称轴的距离小于点A到对称轴的距离,
∴,解得a<2,
∴0≤a<2
②当 ,即a<0时,点B到对称轴的距离小于点A到对称轴的距离,
∴ 成立,
∴a<0
③对称轴在点A左侧不合题意,舍去,
综上所述,a<2.
【点睛】本题考查二次函数图象与系数的关系,二次函数图象上点的坐标特征及二次函数的性质,熟知二次函数的图象和性质及巧用分类讨论的数学思想是解题的关键.
3.已知二次函数y=x2﹣2kx+k﹣2的图象过点(5,5).
(1)求二次函数的表达式.
(2)若A(x1,y1)和B(x2,y2)都是二次函数图象上的点,且x1+2x2=2,求y1+y2的最小值.
(3)若点P(a,n)和Q(b,n+2)都在二次函数的图象上,且a<b.对于某一个实数n,若b﹣a的最小值为1,则b﹣a的最大值为多少?
【点拨】(1)利用待定系数法即可求解;
(2)根据图象上点的坐标特征得出y1+y2=﹣4x1+﹣4x2,由x1+2x2=2可知x1=2﹣2x2,即可求得y1+y2=﹣4x1+﹣4x2=5(x2﹣)2﹣,利用二次函数的性质即可求得最小值;
(3)由题意可知当点P(a,n)和Q(b,n+2)在对称轴的同侧时b﹣a的值最小,当点P(a,n)和Q(b,n+2)在异侧是b﹣a的值最大,据此求解即可.
【解析】解:(1)∵二次函数y=x2﹣2kx+k﹣2的图象过点(5,5),
∴5=25﹣10k+k﹣2,
∴k=2,
∴二次函数的表达式为y=x2﹣4x;
(2)∵A(x1,y1)和B(x2,y2)都是二次函数图象上的点,
∴y1=﹣4x1,y2=﹣4x2,
∴y1+y2=﹣4x1+﹣4x2,
∵x1+2x2=2,
∴x1=2﹣2x2,
∴y1+y2
=﹣4x1+﹣4x2
=(2﹣2x2)2﹣4(2﹣2x2)+﹣4x2
=5﹣4x2﹣4
=5(x2﹣)2﹣,
∵5>0,
∴y1+y2的最小值是﹣;
(3)∵抛物线y=x2﹣4x=(x﹣2)2﹣4,
∴t图象开口向上,对称轴为直线x=2,
∵点P(a,n)和Q(b,n+2)都在二次函数的图象上,且a<b.对于某一个实数n,若b﹣a的最小值为1,
∴点P(a,n)和Q(b,n+2)在对称轴的右侧,此时b﹣a=1,则b=a+1,
∴a2﹣4a=n①,(a+1)2﹣4(a+1)=n+2②,
②﹣①得a=,
∴b=a+1=,
∴此时点P(,n)和Q(,n+2),
当点P是点(,n)的对称点时,则b﹣a的值最大,
∵对称轴为直线x=2,
∴点(,n)的对称点为(,n),
∴此时a=,
∴b﹣a的最大值为:﹣=2.
【点睛】本题考查了待定系数法求二次函数的解析式,二次函数的性质,二次函数的最值,掌握二次函数的性质是解题的关键.
4.定义:对于y关于x的函数,函数在x1≤x≤x2(x1<x2)范围内的最大值,记作M[x1,x2].
如函数y=2x,在﹣1≤x≤3范围内,该函数的最大值是6,即M[﹣1,3]=6.
请根据以上信息,完成以下问题:
已知函数y=(a﹣1)x2﹣4x+a2﹣1(a为常数).
(1)若a=2.
①直接写出该函数的表达式,并求M[1,4]的值;
②已知,求p的值.
(2)若该函数的图象经过点(0,0),且M[﹣3,k]=k,求k的值.
【点拨】(1)①将a值代入运算即可,利用新定义的规定计算即可;
②令y=3,求得x值,再利用新定义的规定解答即可;
(2)利用待定系数法求得a值,再利用分类讨论的方法,依据新定义的规定列出关于k的方程解答即可.
【解析】解:(1)①∵a=2,
∴y=x2﹣4x+3.
∵[1,4],
∴1≤x≤4.
∴当x=4时,y=x2﹣4x+3=3,取得最大值,
∴M[1,4]=3;
②∵,
∴当p≤x≤时,函数y取得最大值3,
令y=3,则x2﹣4x+3=3,
∴x=0或x=4.
∴p=0.
(2)∵该函数的图象经过点(0,0),
∴a2﹣1=0,
∴a=±1.
当a=1时,y=﹣4x,
∵M[﹣3,k]=k,
∴k=﹣4×(﹣3)=12,
∴k=12.
当a=﹣1时,y=﹣2x2﹣4x.
∵y=﹣2(x+1)2+2,
∴当x=﹣1时,y取得最大值为2,
∵M[﹣3,k]=k,
∴﹣2k2﹣4k=k,
∴k=0(不合题意,舍去)或k=﹣.
∵当a=﹣1时,y=﹣2x2﹣4x.
∵y=﹣2(x+1)2+2,
∴当x=﹣1时,y取得最大值为2,
∴k=2.
当﹣3≤x≤2时,函数的最大值为2,
∴k=2.
综上,k的值为12或k=﹣或k=2.
【点睛】本题主要考查了二次函数的解析式,一次函数的性质,待定系数法,二次函数图象的性质,本题是新定义型,正确理解新定义的规定并熟练运用是解题的关键.
5.设二次函数y=ax2+bx+1(a≠0,b是常数),已知函数值y和自变量x的部分对应取值如表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=0时,求二次函数的表达式;
(2)当﹣1≤x≤3时,y有最小值为,求a的值;
(3)若a<﹣3,求证:n﹣m﹣p>20.
【点拨】(1)利用待定系数法解答即可;
(2)利用抛物线的对称性得出抛物线的对称轴为直线x=1,利用二次函数的性质得到当x=1时,函数y取得最小值,再利用待定系数法解答即可;
(3)利用抛物线的对称轴为直线x=1,得到b=﹣2a,则y=ax2﹣2ax+1,利用表格求得m,np的值,并计算出n﹣m﹣p=﹣7a﹣1,再利用不等式的性质解答即可得出结论.
【解析】(1)解:当m=0时,抛物线y=ax2+bx+1经过(﹣1,0),(0,1),(2,1)三点,
∴,
∴,
∴二次函数的表达式为y=﹣x+1;
(2)解:∵抛物线y=ax2+bx+1经过(0,1),(2,1)两点,
∴当x=0或x=2时,y=1,
∴抛物线的对称轴为直线x=1,
∴y=ax2﹣2ax+1,
∵当﹣1≤x≤3时,y有最小值为,
∴如果a>0,当x=1时,函数y取得最小值,
∴,
∴.
∴a的值为;
如果a<0,则x=﹣1或x=3时,函数y取得最小值,
∴a×(﹣1)2﹣2a×(﹣1)+1=,
∴a=﹣.
综上,a的值为或﹣.
(3)证明:由(2)知:抛物线的对称轴为直线x=1,
∴=1,
∴b=﹣2a.
∴y=ax2﹣2ax+1,
∴m=a×(﹣1)2﹣2a×(﹣1)+1=3a+1,n=a﹣2a+1=﹣a+1,p=m=3a+1,
∴n﹣m﹣p=﹣a+1﹣(3a+1)﹣(3a+1)=﹣7a﹣1.
∵a<﹣3,
∴﹣7a>21,
∴﹣7a﹣1>20.
即:n﹣m﹣p>20.
【点睛】本题主要考查了二次函数的性质,待定系数法,抛物线上点的坐标的特征,二次函数的极值,熟练掌握二次函数的性质和待定系数法是解题的关键.
6.(2024 浙江模拟)已知点A(m,p),B(3,q),C(m+2,p)都在二次函数y=2x2+bx+4的图象上.
(1)若m=1,求该二次函数的表达式;
(2)求p+q的最大值;
(3)若p<q<4,求m的取值范围.
【点拨】(1)当m=1时,根据二次函数的对称轴为直线x=﹣==m+1求出b即可;
(2)根据﹣=m+1得出b=﹣4(m+1),然后求出p+q关于m的二次函数解析式,根据函数的性质求最值;
(3)根据p<q<4以及二次函数的性质求出m的取值范围.
【解析】解:(1)根据题意得,二次函数的对称轴为直线x=﹣==m+1,
当m=1时,﹣=2,
∴b=﹣8,
∴二次函数的表达式为y=2x2﹣8x+4;
(2)∵﹣=m+1,
∴b=﹣4(m+1),
把A,B坐标分别代入y=2x2+bx+4得,
p=2m2﹣4(m+1)m+4=﹣2m2﹣4m+4,
q=18﹣4(m+1)×3+4=﹣12m+10,
∴p+q=﹣2m2﹣4m+4﹣12m+10=﹣2m2﹣16m+14=﹣2(m﹣4)2+46,
∵﹣2<0,
∴m=4时,p+q最大值为46;
(3)∵p<q,
∴m>3或m+2<3,
∵q<4,
∴﹣12m+10<4,
解得m>,
∴m的取值范围为<m<1或m>3.
【点睛】本题考查待定系数法求函数解析式、二次函数的最值以及二次函数的性质,关键是利用二次函数的性质解答.
7.已知二次函数y1=ax(x+b)(a≠0)和一次函数y2=ax+m.
(1)若二次函数y1的图象过点(1,0)和(2,2),求二次函数的表达式.
(2)若一次函数y2与二次函数y1的图象交于x轴上同一点A,且A不是原点.
①求证:m=ab;
②若二次函数y1与一次函数y2的另一个交点B为y1的顶点,求b的值.
【点拨】(1)利用待定系数法解答即可;
(2)①令y=0,分别求得两个函数的图象与x轴的交点,依据已知条件列出关于a,b,m的等式,整理即可得出结论;
②利用配方法求得抛物线的顶点坐标,将坐标代入一次函数的解析式,再利用①的结论得到关于b的方程,解方程即可得出结论.
【解析】(1)解:∵二次函数y1的图象过(1,0),(2,2)点,
∴,
解得:,
∴二次函数的表达式为y=x2﹣x;
(2)①证明:令y1=0,则ax(x+b)=0,
解得:x=0或x=﹣b.
∴抛物线y1=ax(x+b)与x轴交于(0,0)(﹣b,0).
令y2=0,则ax+m=0,
∴x=﹣.
∴直线y2=ax+m与x轴交于(﹣,0),
∵若一次函数y2与二次函数y1的图象交于x轴上同一点,且这个点不是原点,
∴﹣=﹣b,
∴m=ab;
②解:∵y1=ax(x+b)=ax2+abx=a(x+)2﹣,
∴二次函数的顶点为(﹣,﹣).
∵两个函数图象的另一个交点为二次函数的顶点,
∴a (﹣)+m=﹣.
由①知:m=ab,
∴﹣+ab=﹣,
解得:b=0(不合题意,舍去)或b=﹣2.
∴若两个函数图象的另一个交点为二次函数的顶点,b的值为﹣2.
【点睛】本题主要考查了二次函数的图象与性质,一次函数的图象与性质,待定系数法,函数图象的交点,抛物线上点的坐标的特征,一次函数图象上点的坐标的特征,熟练掌握待定系数法是解题的关键.
8.(2024 宁波模拟)设一次函数y1=a(x+m)的图象与x轴交于点A,二次函数的图象与x轴交于A,B两个不同的点,设函数y=y1+y2.
(1)设点Q(0,q)在函数y的图象上,若q>c,求证:am>0.
(2)若函数y2,y的图象在x轴上截得的线段长分别为d1,d2,求d1,d2的数量关系式.
(3)若函数y1的图象分别与函数y2的图象、函数y的图象交于点E(x1,e),F(x2,f),且点E,F不同于点A,求x1﹣x2的值.
【点拨】(1)把y1与y2相加得y=ax2+(a+b)x+am+c,把点Q代入y,再计算即可.
(2)设A(t,0),代入y1得y1=a(x﹣t).设B(k,0),又A(t,0)得y2=ax2﹣(at+ak)x+atk,
故y=ax2+(a﹣at﹣ak)x+atk﹣at,设y2=ax2﹣(at+ak)x+atk两根为p、q,再计算即可.
(3)由(2)知y1=a(x﹣t),y2=a(x﹣t)(x﹣k),得a(x﹣t)=a(x﹣t)(x﹣k),计算得x1=k+1.
由y1=a(x﹣t),y=a(x﹣t)+ax2﹣(at+ak)x+atk,得a(x﹣t)=a(x﹣t)+ax2﹣(at+ak)x+atk,计算得x2=k.故x1﹣x2=k+1﹣k=1.
【解析】解:(1)∵y1=a(x+m),,
∴y=y1+y2=a(x+m)+ax2+bx+c=ax2+(a+b)x+am+c,
∵点Q(0,q)在函数y的图象上,
∴q=am+c,
即q﹣c=am,
∵q>c,
∴am>0.
(2)设A(t,0),代入y1=a(x+m)得:
0=a(t+m),
∵a≠0,
∴t+m=0,
∴m=﹣t,
y1=a(x﹣t).
设B(k,0),又A(t,0),
∴y2=a(x﹣t)(x﹣k)=ax2﹣(at+ak)x+atk,
∴y=a(x﹣t)+ax2﹣(at+ak)x+atk=ax2+(a﹣at﹣ak)x+atk﹣at,
设y2=ax2﹣(at+ak)x+atk两根为p、q,
∴p+q==t+k,pq==tk,
∴=(p﹣q)2=(p+q)2﹣4pq=(t+k)2﹣4tk=t2+k2﹣2tk,
即=t2+k2﹣2tk=(t﹣k)2,
∴d1=,
设y=ax2+(a﹣at﹣ak)x+atk﹣at两根为r、s,
∴r+s==k+t﹣1,rs==kt﹣t,
∴=(r﹣s)2=(r+s)2﹣4rs=(k+t﹣1)2﹣4(kt﹣t)=k2+t2﹣2tk﹣2k+2t+1,
∴﹣=|(t2+k2﹣2tk)﹣(k2+t2﹣2tk﹣2k+2t+1)|=|2(k﹣t)﹣1|=±2d1﹣1,
答:d1,d2的数量关系式是:﹣=±2d1﹣1.
(3)由(2)知y1=a(x﹣t),y2=a(x﹣t)(x﹣k),
得a(x﹣t)=a(x﹣t)(x﹣k),
∴a(x﹣t)(x﹣k)﹣a(x﹣t)=0,
∴a(x﹣t)(x﹣k﹣1)=0,
∴x=t,x=k+1,
即A(t,0),x1=k+1.
由y1=a(x﹣t),y=a(x﹣t)+ax2﹣(at+ak)x+atk,
得a(x﹣t)=a(x﹣t)+ax2﹣(at+ak)x+atk,
∴ax2﹣(at+ak)x+atk=0,
∴x2﹣(t+k)x+tk=0,
∴(x﹣t)(x﹣k)=0,
∴x=t,x=k,
即A(t,0),x2=k.
∴x1﹣x2=k+1﹣k=1.
【点睛】本题考查了抛物线的知识,掌握抛物线的性质是解题关键.
9.如图,小车从点A出发,沿与水平面成30°角光滑斜坡AB下滑,在下滑过程中小车速度逐渐增加,设小车出发点A离水平地面BE的高度为h,小车从点A滑行到最低点B所用的时间为t(秒),小车滑行到点B时的速度为v(厘米/秒).速度v与时间t满足关系:v=10t,高度h与时间t满足关系:(g≠0,g是常数),当小车出发点小车出发点A离水平地面BE的高度为20(厘米)时,小车从点A滑到最低点B需要2秒.
(1)当小车出发点A离水平地面BE的高度为45(厘米)时,小车滑到最低点B需要几秒钟?此时小车到达B点时的速度是多少?
(2)小车继续在粗糙的水平地面BE上滑行,设滑行的距离为s(厘米),小车从斜坡滑行到点B时速度为v(厘米/秒),小车在水平地面BE上滑行的时间为T(秒),若s与v,T之间满足以下关系:+vT(a≠0,a是常数),当v=20(厘米/秒)时,s=50(厘米),T=5(秒).如果把小车出发点A离水平地面BE的距离h提高到125厘米,那么当滑行到时间T=4秒时,小车在水平地面BE上滑行的距离为多少?
【点拨】(1)先根据已知条件求出g的值,求出高度h与时间t的函数解析式,再把h=45代入解析式求出t,再把t的值代入y=10t求出速度v;
(2)先把v=20,s=50,T=5代入+vT求出a的值,再根据h=125求出t,再求出v,然后求出s即可.
【解析】解:(1)当t=2,h=20时,20=g×22,
解得g=10,
∴h=×10t2=5t2;
∴当h=45时,5t2=45,
解得t=3或t=﹣3(舍去),
此时v=10×3=30(cm/s),
答:当小车出发点A离水平地面BE的高度为45(厘米)时,小车滑到最低点B需要3秒钟,此时小车到达B点时的速度是30厘米/秒;
(2)把v=20,s=50,T=5代入+vT,
则50=﹣a×52+20×5,
解得a=4,
∴s=﹣2T2+vT,
当h=125时,5t2=125,
解得t=5或t=﹣5(舍去),
∴v=10×5=50(cm/s),
∴s=﹣2×42+50×4=168(cm).
答:小车在水平地面BE上滑行的距离为168cm.
【点睛】本题考查二次函数的应用,关键是待定系数法求函数解析式.
10.(2024 北仑区一模)周末,小明和同学们一起去长江路地铁站坐地铁.在等车的过程中,他惊叹于地铁每次都能精准的停靠在停止线上.为什么每次地铁停靠都那么准呢?里面一定包含着数学知识!通过工作人员帮助,小明获得了地铁刹车开始的时间t与地铁到停止线的距离S之间的表格信息:
t(秒) 0 4 8 12 16 20 24 …
S(米) 256 196 144 100 64 36 16 …
当小明拿到这些数据时,他作了如下的思考:
(1)依据数学经验,小明需要将这些数据绘制在平面直角坐标系中,并用平滑的曲线进行连线,形成数据所生成的图象,请你在图中落实他的想法;
(2)根据图象以及数据关系,它可能是我们所学习过的 二次 函数图象(选填“一次”、“二次”或“反比例”).请你选择合适的数据求出该函数的表达式;
(3)地铁从开始刹车到下次启动一共用时60秒.求地铁的停靠时间.
(停靠时间指的是地铁刹停后的静止时间)
【点拨】(1)根据描点,连线,画出函数图象即可求解;
(2)观察函数图象即可求解;待定系数法求二次函数解析式即可求解;
(3)将S=0代入,解方程即可求出t的值,再用60﹣t即可得出结论.
【解析】解:(1)描点,连线,如图:
(2)根据图象以及数据关系,它可能是我们所学习过的二次函数,
设S=at2+bt+c,将点(0,256)代入得:c=256,
将(4,196),(8,144)代入S=ax2+bx+256中,
得:,
解得:,
∴该函数的表达式为S=x2﹣16x+256;
故答案为:二次;
(3)依题意,当S=0时,x2﹣16x+256=0,
解得:t1=t2=32,
∴60﹣32=28,
∴地铁的停靠时间为28秒.
【点睛】本题考查了二次函数的应用,熟练掌掌握二次函数性质是解题的关键.
11.(2024 浙江模拟)某个农场有一个花卉大棚,是利用部分墙体建造的.其横截面顶部为抛物线型,大棚的一端固定在墙体OA上,另一端固定在墙体BC上,其横截面有2根支架DE,FG,相关数据如图1所示,其中支架DE=BC,OF=DF=BD,这个大棚用了400根支架.
为增加棚内空间,农场决定将图1中棚顶向上调整,支架总数不变,对应支架的长度变化,如图2所示,调整后C与E上升相同的高度,增加的支架单价为60元/米(接口忽略不计),需要增加的经费不超过32000元.
(1)分别以OB和OA所在的直线为x轴和y轴建立平面直角坐标系.
①求出改造前的函数解析式.
②当CC′=1米,求GG′的长度.
(2)只考虑经费情况下,求出CC′的最大值.
【点拨】(1)①设改造前的函数解析式为y=ax2+bx+c,根据所建立的平面直角坐标系得到A(0,1),E(4,3.4),C(6,3.4),然后代入解析式得到关于a、b、c的方程组,求解即可;
②根据已知条件得到函数的解析式,再利用函数解析式得到C′、E′的坐标即可得到结论;
(2)根据已知条件表示出G′、E′的坐标得到a的不等式,进而得到CC′的最大值.
【解析】解:(1)①如图,以O为原点,分别以OB和OA所在的直线为x轴和y轴建立如图所示的平面直角坐标系,
由题意可知:A(0,1),E(4,3.4),C(6,3.4),
设改造前的抛物线解析式为y=ax2+bx+c,
∴,
解得:,
∴改造前的抛物线的函数表达式为;
②如图,建立与(1)相同的平面直角坐标系,
由①知改造前抛物线的解析式为,
∴对称轴为直线,
设改造后抛物线解析式为:,
∵调整后C与E上升相同的高度,且CC′=1,
∴对称轴为直线x=5,则有,
当x=6时,y=4.4,
∴36c+6d+1=4.4,
∴,,
∴改造后抛物线解析式为:,
当x=2时,
改造前:,
改造后:,
∴(米),
∴GG′的长度为米;
(2)如(2)题图,设改造后抛物线解析式为y=ax2﹣10ax+1,
∵当x=2时,y=a×22﹣10a×2+1=﹣16a+1,
当x=4时,y=a×42﹣10a×4+1=﹣24a+1,
∴G′(2,﹣16a+1),E′(4,﹣24a+1),
∴,
由题意可列不等式:(﹣40a﹣4)×200×60≤32000,
解得:,
∵CC'=EE'=﹣24a+1﹣3.4,
要使最大,需a最小,
∴当时,CC′的值最大,最大值为1.6米.
【点睛】本题考查用待定系数法求二次函数的解析式,二次函数的对称轴,二次函数的实际应用,一元一次不等式的实际应用等知识点.掌握二次函数的性质及是一元一次不等式的应用解题的关键.
12.(2024 镇海区一模)根据以下素材,探索完成任务.
设计跳长绳方案
素材1:某校组织跳长绳比赛,要求如下:(1)每班需要报名跳绳同学9人,摇绳同学2人;(2)跳绳同学需站成一路纵队,原地起跳,如图1.
素材2:某班进行赛前训练,发现:(1)当绳子摇至最高处或最低处时,可近似看作两条对称分布的抛物线,已知摇绳同学之间水平距离为6m,绳子最高点为2m,摇绳同学的出手高度均为1m,如图2;(2)9名跳绳同学身高如右表. 身高(m)1.701.731.751.80人数2241
素材3:观察跳绳同学的姿态(如图3),发现:(1)跳绳时,人的跳起高度在0.25m及以下较为舒适;(2)当长绳摇至最高处时,人正屈膝落地,此时头顶到地面的高度是身高的.
问题解决
任务1:确定长绳形状.请在图2中以长绳触地点为原点建立直角坐标系,并求出长绳摇至最高处时,对应抛物线的解析式.
任务2:确定排列方案.该班班长决定:以长绳的触地点为中心,将同学按“中间高,两边低”的方式对称排列,同时保持0.45m的间距.请计算当绳子在最高点时,长绳是否会触碰到最边侧的同学.
任务3:方案优化改进.据最边侧同学反映:由于跳起高度过高,导致不舒适,希望作出调整.班长给出如下方案:摇绳同学在绳即将触地时,将出手高度降低至0.85m.此时中段长绳将贴地形成一条线段(x线段AB),而剩余的长绳则保持形状不变,如图4.请你通过计算说明,该方案是否可解决同学反映的问题.
【点拨】(1)按照题意建立平面直角坐标系,易得抛物线的对称轴为y轴,于y轴交于点(0,2),并且经过点(﹣3,1),设出相应的函数解析式,进而把点(﹣3,1)代入可得二次项系数的值,即可求得长绳摇至最高处时,对应抛物线的解析式;
(2)9个同学,最高的同学在正中间,那么右边将有4个同学,易得最右侧同学所在的横坐标,代入(1)中得到的解析式,可得最右侧同学所在的地方抛物线的高度,计算出最右侧同学屈膝后的身高,与抛物线的高度比较可判断绳子在最高点时,长绳是否会触碰到最边侧的同学;
(3)根据抛物线的形状相同可得绳子摇至最低处时,抛物线解析式,进而可得平移后新的抛物线解析式,取最右侧同学的横坐标代入可得最右侧同学跳绳的高度,与舒适高度0.25比较即可判断方案能否解决问题.
【解析】解:任务1:如图建立平面直角坐标系.
设长绳摇至最高处时,对应抛物线的解析式为:y=ax2+2(a≠0).
∵经过点(﹣3,1).
∴9a+2=1.
解得:a=﹣.
∴长绳摇至最高处时,对应抛物线的解析式为:y=﹣x2+2.
任务2.最右侧同学所在的横坐标为:0.45×4=1.8.
当x=1.8时,y=﹣×(1.8)2+2=1.64.
∵长绳摇至最高处时,人正屈膝落地,此时头顶到地面的高度是身高的,
∴最右侧同学屈膝后的身高为:1.70×=1.615.
∵1.615<1.64.
∴绳子在最高点时,长绳不会触碰到最边侧的同学.
任务3.当绳子摇至最低处时,抛物线解析式可表示为y=x2.
∵出手高度降低至0.85m.
∴抛物线下降0.15m.
∴下移后的抛物线解析式为:y=x2﹣0.15.
当x=1.8时,y=×1.82﹣0.15=0.21.
∵0.21<0.25,
∴方案能解决同学反映的问题.
【点睛】本题考查二次函数的应用.用到的知识点为:二次函数的形状相同,开口方向不同,则两个函数二次项的系数互为相反数;二次函数上下平移,只改变函数值,上加下减.
13.(2024 上城区校级模拟)
设计喷水方案
素材1 图1为某公园的圆形喷水池,图2是其示意图,O为水池中心,喷头A、B之间的距离为20米,喷射水柱呈抛物线形,水柱距水池中心7m处达到最高,高度为5m,水池中心处有一个圆柱形蓄水池,其底面直径CD为12m,高CF为1.8米
素材2 如图3、图4,拟将在圆柱形蓄水池中心处建一能伸缩高度的喷水装置OP(OP⊥CD),要求水柱不能碰到图2中的水柱,也不能落在蓄水池外面.经调研,目前市场有两种喷水头均能喷射与图2中形状相同的抛物线.其中,甲喷水头以点P为最高点向四周喷射水柱(如图3),乙喷水头喷射水柱的最高点与点P的高度差为0.8m(如图4).
问题解决
任务1 确定水柱形状 在图2中以点O为坐标原点,水平方向为轴建立直角坐标系,求左边这条抛物线的函数表达式.
任务2 选择喷水装置甲,确定喷水装置的最高高度 若选择甲装置(图3),为防止水花溅出,当落水点G、M之间的距离满足时,OP不能再升高,求此时OP的最高高度.
任务3 选择喷水装置乙,拟定喷水装置的高度范围 若选择乙装置(图4),为了美观,要求OP喷出的水柱高度不低于5m,求喷水装置OP高度的变化范围.
【点拨】任务1.易得左侧抛物线的顶点坐标为(﹣7,5)以及点A的坐标(﹣10,0).用顶点式表示出所求的抛物线解析式,把点A的坐标代入即可求得二次函数的二次项系数,即可求得抛物线的解析式;
任务2.设OP长m米,则点P的坐标为(0,m).可设甲喷水头形成的抛物线解析式为:y=﹣x2+m.根据任务1中的抛物线解析式可得点M的坐标,进而可得FM的长度,根据GM=FM,可得GM的长度,即可求得点G的坐标,代入所设的抛物线解析式,即可求得m的值,也就求出了OP的最高高度;
任务3.乙喷水头喷出的抛物线的顶点坐标可设为:(h,m+0.8).用顶点式表示出乙喷水头喷出的抛物线的解析式,把点P的坐标代入可得h的值,进而根据OP喷出的水柱高度不低于5m,取顶点的纵坐标不低于5可得m的一个范围,进而根据水柱不能碰到图2中的水柱,也不能落在蓄水池外面.取点M的坐标代入所求的抛物线解析式可得m的值,即可求得m的取值范围,也就求得了喷水装置OP高度的变化范围.
【解析】解:任务1.如图以点O为坐标原点,水平方向为x轴建立直角坐标系.
∵A、B之间的距离为20米,
∴点A的坐标为(﹣10,0).
∵水柱距水池中心7m处达到最高,高度为5m,
∴左侧抛物线的顶点坐标为(﹣7,5).
∴设左侧抛物线的解析式为:y=a(x+7)2+5.
∴a(﹣10+7)2+5=0.
解得:a=﹣.
∴左边抛物线的函数表达式为:y=﹣(x+7)2+5.
任务2.设OP长m米,则点P的坐标为(0,m).
∵甲喷水头喷射与图2中形状相同的抛物线,并且两个抛物线的开口方向相同.
∴甲喷水头形成的抛物线解析式为:y=﹣x2+m.
由任务1得:左边抛物线的函数表达式为:y=﹣(x+7)2+5.
当y=1.8时,1.8=﹣(x+7)2+5.
解得:x1=﹣9.4(不合题意,舍去),x2=﹣4.6.
∴点M的横坐标为:﹣4.6.
∵CD为12m,
∴OC=6m.
∴FM=6﹣|﹣4.6|=1.4.
∵GM=FM,
∴GM=0.4.
∴点G的横坐标是﹣4.6+0.4=﹣4.2.
∴点G的坐标是(﹣4.2,1.8).
∴1.8=﹣×(﹣4.2)2+m.
解得:m=.
∴OP的最高高度为米.
任务3.如图,建立平面直角坐标系.以y轴左侧的抛物线为例.
设OP长m米,则点P的坐标为(0,m).
∵乙喷水头喷射水柱的最高点与点P的高度差为0.8 m,
∴乙喷水头喷出的抛物线的顶点坐标可设为:(h,m+0.8).
∵乙喷水头喷射与图2中形状相同的抛物线,并且两个抛物线的开口方向相同.
∴乙喷水头形成的抛物线解析式为:y=﹣(x﹣h)2+m+0.8.
把点P的坐标代入得:m=﹣(0﹣h)2+m+0.8.
解得:h=﹣1.2或h=1.2(不合题意,舍去).
∴乙喷水头形成的抛物线解析式为:y=﹣(x+1.2)2+m+0.8.
∵OP喷出的水柱高度不低于5m,
∴最高点(h,m+0.8)的纵坐标不低于5m.
∴m+0.8≥5.
解得:m≥.
∵水柱不能碰到图2中的水柱,也不能落在蓄水池外面.
∴取点M的坐标(﹣4.6,1.8)代入y=﹣(x+1.2)2+m+0.8.
1.8=﹣(﹣4.6+1.2)2+m+0.8.
解得:m=.
∴m<.
∴≤m<.
∴喷水装置OP高度的变化范围为:≤OP<.
【点睛】本题考查二次函数的应用.用到的知识点为:二次函数的形状相同,且开口方向相同,则二次函数的二次项的系数相同.
14.(2024 西湖区一模)在平面直角坐标系中,点(1,m)和(3,n)都在二次函数y=ax2+bx(a≠0,a,b是常数)的图象上.
(1)若m=n=﹣6,求该二次函数的表达式和函数图象的对称轴.
(2)若a=﹣1,m<n,求b的取值范围.
(3)已知点(﹣1,y1),(2,y2),(4,y3)也都在该二次函数图象上,若mn<0且a<0,试比较y1,y2,y3的大小,并说明理由.
【点拨】(1)当m=n=﹣6时,用待定系数法可得二次函数的表达式为y=2x2﹣8x;即可得函数图象的对称轴为直线x=2;
(2)当a=﹣1时,可得,又m<n,故﹣1+b<﹣9+3b,得b>4;
(3)由mn<0,可得(a+b)(9a+3b)<0,又a<0,即可知a+b>0且3a+b<0;求出y1=a﹣b,y2=4a+2b,y3=16a+4b,用作差的方法可得到答案.
【解析】解:(1)当m=n=﹣6时,把(1,﹣6)和(3,﹣6)代入y=ax2+bx得:
,
解得,
∴二次函数的表达式为y=2x2﹣8x;
∵y=2x2﹣8x=2(x﹣2)2﹣8,
∴函数图象的对称轴为直线x=2;
(2)当a=﹣1时,y=﹣x2+bx,
把(1,m)和(3,n)代入得:
,
∵m<n,
∴﹣1+b<﹣9+3b,
解得b>4,
∴b的取值范围是b>4;
(3)把(1,m)和(3,n)代入y=ax2+bx得:
,
∵mn<0,
∴(a+b)(9a+3b)<0,
∴或,
∵a<0,
∴,即无解;
∴a+b>0且3a+b<0;
把(﹣1,y1),(2,y2),(4,y3)代入y=ax2+bx得:
y1=a﹣b,y2=4a+2b,y3=16a+4b,
∴y1﹣y2=a﹣b﹣(4a+2b)=﹣3(a+b)<0,y1﹣y3=a﹣b﹣(16a+4b)=﹣5(3a+b)>0,
∴y1<y2,y1>y3,
∴y3<y1<y2.
【点睛】本题考查二次函数的综合应用,涉及待定系数法,二次函数图象上点坐标的特征,作差法比较大小等,解题的关键是掌握二次函数图象上点坐标的特征和不等式的基本性质.
15.如图,二次函数y=ax2+bx+3(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,C为顶点.
(1)请求出二次函数的表达式及图象的顶点C的坐标.
(2)若点E为抛物线对称轴左侧一点,过点E作x轴平行线交对称轴于点D,若ED=m,试用m的代数式表示CD.
(3)连结EC,过点C作CF⊥EC交抛物线于点F,过点F作x轴的平行线交对称轴于点G,证明:GF DE=1.
【点拨】(1)用待定系数法求函数的解析式即可;
(2)设D(1,t),可得E(1﹣m,t),又由t=﹣(1﹣m)2+2(1﹣m)+3,能求CD=4﹣t=m2;
(3)证明△CDE∽△FGC,可得=,推导出FG=mCG,设F(n,﹣n2+2n+3),则G(1,﹣n2+2n+3),则CG=(n﹣1)2,所以n﹣1=,再由FG=mCG,可求GF DE=mFG=m2 (n﹣1)2=1.
【解析】(1)解:将点A(﹣1,0),B(3,0)代入y=ax2+bx+3,
∴,
解得,
∴抛物线的解析式为y=﹣x2+2x+3;
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点C(1,4);
(2)解:设D(1,t),
∵ED=m,
∴E(1﹣m,t),
∴t=﹣(1﹣m)2+2(1﹣m)+3,
∴CD=4﹣t=m2;
(3)证明:∵ED⊥CD,GF⊥CD,
∴∠EDC=∠CGF=90°,
∵EC⊥CF,
∴∠ECF=90°,
∵∠ECD+∠FCG=90°,∠ECD+∠CED=90°,
∴∠FCG=∠CED,
∴△CDE∽△FGC,
∴=,
∴GF DE=GC CD,
∵ED=m,CD=m2,
∴FG=mCG,
设F(n,﹣n2+2n+3),则G(1,﹣n2+2n+3),
∴CG=4﹣(﹣n2+2n+3)=(n﹣1)2,
∴n﹣1=m(n﹣1)2,
∴n﹣1=,
∵FG=mCG,
∴GF DE=mFG=m2 (n﹣1)2=1.
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,三角形相似的判定及性质是解题的关键.
16.已知二次函数的图象经过原点O和点A(8+t,0),其中t≥0.
(1)当t=0时.
①求y关于x的函数表达式,并求出当x为何值时,y有最大值,最大值为多少?
②当x=m和x=n时(m≠n),函数值相等,求m,n之间的关系式.
(2)当t>0时,在0≤x≤8范围内,y是否存在最大值18?若存在,求出相应的t和x的值,若不存在,请说明理由.
【点拨】(1)①把O(0,0),A(8,0)代入y=﹣x2+bx+c得,可求出y关于x的函数表达式为y=﹣x2+2x;而y=﹣x2+2x=﹣(x﹣4)2+4,故当x为4时,y有最大值,最大值为4;
②根据当x=m和x=n时(m≠n),函数值相等,可得﹣(m﹣4)2+4=﹣(n﹣4)2+4,即可求出m+n=8;
(2)把二次函数的图象经过原点O和点A(8+t,0),,可求出y=﹣x2+x=﹣(x﹣)2+,故抛物线y=﹣x2+x的对称轴为直线x=;①当≥8,即t≥8时,﹣×82+×8=18,解得t的值即可知当t的值为9,x的值为8时,y取得最大值18;②当<8,即0<t<8时,有=18,可解得:t=﹣12﹣8(小于0,舍去)或t=12﹣8(大于8,舍去).
【解析】解:(1)当t=0时,A(8,0),
①把O(0,0),A(8,0)代入y=﹣x2+bx+c得:
,
解得:,
∴y关于x的函数表达式为y=﹣x2+2x;
∵y=﹣x2+2x=﹣(x﹣4)2+4,
∴当x为4时,y有最大值,最大值为4;
②∵当x=m和x=n时(m≠n),函数值相等,
∴﹣(m﹣4)2+4=﹣(n﹣4)2+4,
∴(m﹣n)(m+n﹣8)=0,
∵m﹣n≠0,
∴m+n=8;
(2)在0≤x≤8范围内,y存在最大值18,理由如下:
∵二次函数的图象经过原点O和点A(8+t,0),
∴,
解得,
∴y=﹣x2+x=﹣(x﹣)2+,
∴抛物线y=﹣x2+x的对称轴为直线x=;
①当≥8,即t≥8时,
x=8,y=﹣x2+x取得最大值,
∴﹣×82+×8=18,
解得:t=9,
∴当t的值为9,x的值为8时,y取得最大值18;
②当<8,即0<t<8时,
y=﹣x2+x在顶点处取最大值,
∴=18,
解得:t=﹣12﹣8(小于0,舍去)或t=12﹣8(大于8,舍去),
综上所述,当t的值为9,x的值为8时,y取得最大值18.
【点睛】本题考查二次函数综合应用,涉及待定系数法,二次函数图象上点坐标的特征等知识,解题的关键是分类讨论思想的应用.
09 押浙江卷第23题
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
押题方向:二次函数应用及综合问题
2023年浙江真题 考点 命题趋势
2023年湖州卷第21题 二次函数的应用 从近几年浙江各地中考来看,解答题中二次函数考查内容主要是二次函数的实际应用、二次函数综合,其中二次函数的综合题经常以压轴题出现,试题的整体难度比较高,预计2024年浙江卷还将重视二次函数综合问题的考查。
2023年湖州卷、衢州卷、绍兴卷、舟山、嘉兴卷、丽水卷第23题、杭州卷第22题、金华卷第24题 二次函数的综合
1.(2023 杭州)设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
2.(2023 丽水)已知点(﹣m,0)和(3m,0)在二次函数y=ax2+bx+3(a,b是常数,a≠0)的图象上.
(1)当m=﹣1时,求a和b的值;
(2)若二次函数的图象经过点A(n,3)且点A不在坐标轴上,当﹣2<m<﹣1时,求n的取值范围;
3.(2023 宁波)如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).
(1)求该二次函数的表达式及图象的顶点坐标.
(2)当y≤﹣2时,请根据图象直接写出x的取值范围.
4.(2023 绍兴)已知二次函数y=﹣x2+bx+c.
(1)当b=4,c=3时,
①求该函数图象的顶点坐标;
②当﹣1≤x≤3时,求y的取值范围;
(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.
5.(2023 湖州)某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量y(千克)与销售价格x(元/千克)(30≤x<60)存在一次函数关系,部分数据如表所示:
销售价格x(元/千克) 50 40
日销售量y(千克) 100 200
(1)试求出y关于x的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为W元,如果不考虑其他因素,求当销售价格x为多少时,日销售利润W最大?最大的日销售利润是多少元?
6.(2023 温州)一次足球训练中,小明从球门正前方8m的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素);
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25m处?
7.(2023 湖州)如图1,在平面直角坐标系xOy中,二次函数y=x2﹣4x+c的图象与y轴的交点坐标为(0,5),图象的顶点为M.矩形ABCD的顶点D与原点O重合,顶点A,C分别在x轴,y轴上,顶点B的坐标为(1,5).
(1)求c的值及顶点M的坐标.
(2)如图2,将矩形ABCD沿x轴正方向平移t个单位(0<t<3)得到对应的矩形A′B′C′D′.已知边C′D′,A′B′分别与函数y=x2﹣4x+c的图象交于点P,Q,连接PQ,过点P作PG⊥A′B′于点G.
①当t=2时,求QG的长;
②当点G与点Q不重合时,是否存在这样的t,使得△PGQ的面积为1?若存在,求出此时t的值;若不存在,请说明理由.
8.(2023 金华)如图,直线y=与x轴,y轴分别交于点A,B,抛物线的顶点P在直线AB上,与x轴的交点为C,D,其中点C的坐标为(2,0),直线BC与直线PD相交于点E.
(1)如图2,若抛物线经过原点O.
①求该抛物线的函数表达式;
②求的值.
(2)连结PC,∠CPE与∠BAO能否相等?若能,求符合条件的点P的横坐标;若不能,试说明理由.
9.(2023 浙江)在二次函数y=x2﹣2tx+3(t>0)中.
(1)若它的图象过点(2,1),则t的值为多少?
(2)当0≤x≤3时,y的最小值为﹣2,求出t的值;
(3)如果A(m﹣2,a),B(4,b),C(m,a)都在这个二次函数的图象上,且a<b<3.求m的取值范围.
10.(2023 衢州)某龙舟队进行500米直道训练,全程分为启航,途中和冲刺三个阶段.图1,图2分别表示启航阶段和途中阶段龙舟划行总路程s(m)与时间t(s)的近似函数图象.启航阶段的函数表达式为s=kt2(k≠0);途中阶段匀速划行,函数图象为线段;在冲刺阶段,龙舟先加速后匀速划行,加速期龙舟划行总路程s(m)与时间t(s)的函数表达式为s=k(t﹣70)2+h(k≠0).
(1)求出启航阶段s(m)关于t(s)的函数表达式(写出自变量的取值范围).
(2)已知途中阶段龙舟速度为5m/s.
①当t=90s时,求出此时龙舟划行的总路程.
②在距离终点125米处设置计时点,龙舟到达时,t≤85.20s视为达标.请说明该龙舟队能否达标.
(3)冲刺阶段,加速期龙舟用时1s将速度从5m/s提高到5.25m/s,之后保持匀速划行至终点.求该龙舟队完成训练所需时间(精确到0.01s).
1.二次函数的应用:应用待定系数法,根据条件准确得到表达式是解题关键.
2.二次函数的综合问题:熟练掌握待定系数法求函数的解析式,一次函数的图象与性质,二次函数的图象与性质,函数图象上点的特征是解题的关键.
3.要重视数形结合在解决二次函数综合问题中的作用.
1.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
2.在二次函数y=﹣x2+ax+1中(a≠0).
(1)当a=2时,
①求该二次函数图象的顶点坐标;
②当0≤x≤3时,求y的取值范围;
(2)若A(a﹣2,b),B(a,c)两点都在这个二次函数的图象上,且b<c,求a的取值范围.
3.已知二次函数y=x2﹣2kx+k﹣2的图象过点(5,5).
(1)求二次函数的表达式.
(2)若A(x1,y1)和B(x2,y2)都是二次函数图象上的点,且x1+2x2=2,求y1+y2的最小值.
(3)若点P(a,n)和Q(b,n+2)都在二次函数的图象上,且a<b.对于某一个实数n,若b﹣a的最小值为1,则b﹣a的最大值为多少?
4.定义:对于y关于x的函数,函数在x1≤x≤x2(x1<x2)范围内的最大值,记作M[x1,x2].
如函数y=2x,在﹣1≤x≤3范围内,该函数的最大值是6,即M[﹣1,3]=6.
请根据以上信息,完成以下问题:
已知函数y=(a﹣1)x2﹣4x+a2﹣1(a为常数).
(1)若a=2.
①直接写出该函数的表达式,并求M[1,4]的值;
②已知,求p的值.
(2)若该函数的图象经过点(0,0),且M[﹣3,k]=k,求k的值.
5.设二次函数y=ax2+bx+1(a≠0,b是常数),已知函数值y和自变量x的部分对应取值如表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=0时,求二次函数的表达式;
(2)当﹣1≤x≤3时,y有最小值为,求a的值;
(3)若a<﹣3,求证:n﹣m﹣p>20.
6.已知点A(m,p),B(3,q),C(m+2,p)都在二次函数y=2x2+bx+4的图象上.
(1)若m=1,求该二次函数的表达式;
(2)求p+q的最大值;
(3)若p<q<4,求m的取值范围.
7.已知二次函数y1=ax(x+b)(a≠0)和一次函数y2=ax+m.
(1)若二次函数y1的图象过点(1,0)和(2,2),求二次函数的表达式.
(2)若一次函数y2与二次函数y1的图象交于x轴上同一点A,且A不是原点.
①求证:m=ab;
②若二次函数y1与一次函数y2的另一个交点B为y1的顶点,求b的值.
8.设一次函数y1=a(x+m)的图象与x轴交于点A,二次函数的图象与x轴交于A,B两个不同的点,设函数y=y1+y2.
(1)设点Q(0,q)在函数y的图象上,若q>c,求证:am>0.
(2)若函数y2,y的图象在x轴上截得的线段长分别为d1,d2,求d1,d2的数量关系式.
(3)若函数y1的图象分别与函数y2的图象、函数y的图象交于点E(x1,e),F(x2,f),且点E,F不同于点A,求x1﹣x2的值.
9.如图,小车从点A出发,沿与水平面成30°角光滑斜坡AB下滑,在下滑过程中小车速度逐渐增加,设小车出发点A离水平地面BE的高度为h,小车从点A滑行到最低点B所用的时间为t(秒),小车滑行到点B时的速度为v(厘米/秒).速度v与时间t满足关系:v=10t,高度h与时间t满足关系:(g≠0,g是常数),当小车出发点小车出发点A离水平地面BE的高度为20(厘米)时,小车从点A滑到最低点B需要2秒.
(1)当小车出发点A离水平地面BE的高度为45(厘米)时,小车滑到最低点B需要几秒钟?此时小车到达B点时的速度是多少?
(2)小车继续在粗糙的水平地面BE上滑行,设滑行的距离为s(厘米),小车从斜坡滑行到点B时速度为v(厘米/秒),小车在水平地面BE上滑行的时间为T(秒),若s与v,T之间满足以下关系:+vT(a≠0,a是常数),当v=20(厘米/秒)时,s=50(厘米),T=5(秒).如果把小车出发点A离水平地面BE的距离h提高到125厘米,那么当滑行到时间T=4秒时,小车在水平地面BE上滑行的距离为多少?
10.周末,小明和同学们一起去长江路地铁站坐地铁.在等车的过程中,他惊叹于地铁每次都能精准的停靠在停止线上.为什么每次地铁停靠都那么准呢?里面一定包含着数学知识!通过工作人员帮助,小明获得了地铁刹车开始的时间t与地铁到停止线的距离S之间的表格信息:
t(秒) 0 4 8 12 16 20 24 …
S(米) 256 196 144 100 64 36 16 …
当小明拿到这些数据时,他作了如下的思考:
(1)依据数学经验,小明需要将这些数据绘制在平面直角坐标系中,并用平滑的曲线进行连线,形成数据所生成的图象,请你在图中落实他的想法;
(2)根据图象以及数据关系,它可能是我们所学习过的 二次 函数图象(选填“一次”、“二次”或“反比例”).请你选择合适的数据求出该函数的表达式;
(3)地铁从开始刹车到下次启动一共用时60秒.求地铁的停靠时间.
(停靠时间指的是地铁刹停后的静止时间)
11.已知二次函数y=ax2+bx+c(a≠0),且a>b>c,a+b+c=0.
(1)当b=0时,求方程ax2+bx+c=0的根;
(2)已知该二次函数的对称轴为x=m,求证:;
(3)已知该二次函数的图象与x轴,y轴分别交于A(x1,0),B(x2,0),C(0,c)三点(A在B的左侧),且x1+4x2=0,若△ABC为直角三角形,求该二次函数表达式.
11.某个农场有一个花卉大棚,是利用部分墙体建造的.其横截面顶部为抛物线型,大棚的一端固定在墙体OA上,另一端固定在墙体BC上,其横截面有2根支架DE,FG,相关数据如图1所示,其中支架DE=BC,OF=DF=BD,这个大棚用了400根支架.
为增加棚内空间,农场决定将图1中棚顶向上调整,支架总数不变,对应支架的长度变化,如图2所示,调整后C与E上升相同的高度,增加的支架单价为60元/米(接口忽略不计),需要增加的经费不超过32000元.
(1)分别以OB和OA所在的直线为x轴和y轴建立平面直角坐标系.
①求出改造前的函数解析式.
②当CC′=1米,求GG′的长度.
(2)只考虑经费情况下,求出CC′的最大值.
12.根据以下素材,探索完成任务.
设计跳长绳方案
素材1:某校组织跳长绳比赛,要求如下:(1)每班需要报名跳绳同学9人,摇绳同学2人;(2)跳绳同学需站成一路纵队,原地起跳,如图1.
素材2:某班进行赛前训练,发现:(1)当绳子摇至最高处或最低处时,可近似看作两条对称分布的抛物线,已知摇绳同学之间水平距离为6m,绳子最高点为2m,摇绳同学的出手高度均为1m,如图2;(2)9名跳绳同学身高如右表. 身高(m)1.701.731.751.80人数2241
素材3:观察跳绳同学的姿态(如图3),发现:(1)跳绳时,人的跳起高度在0.25m及以下较为舒适;(2)当长绳摇至最高处时,人正屈膝落地,此时头顶到地面的高度是身高的.
问题解决
任务1:确定长绳形状.请在图2中以长绳触地点为原点建立直角坐标系,并求出长绳摇至最高处时,对应抛物线的解析式.
任务2:确定排列方案.该班班长决定:以长绳的触地点为中心,将同学按“中间高,两边低”的方式对称排列,同时保持0.45m的间距.请计算当绳子在最高点时,长绳是否会触碰到最边侧的同学.
任务3:方案优化改进.据最边侧同学反映:由于跳起高度过高,导致不舒适,希望作出调整.班长给出如下方案:摇绳同学在绳即将触地时,将出手高度降低至0.85m.此时中段长绳将贴地形成一条线段(x线段AB),而剩余的长绳则保持形状不变,如图4.请你通过计算说明,该方案是否可解决同学反映的问题.
13.
设计喷水方案
素材1 图1为某公园的圆形喷水池,图2是其示意图,O为水池中心,喷头A、B之间的距离为20米,喷射水柱呈抛物线形,水柱距水池中心7m处达到最高,高度为5m,水池中心处有一个圆柱形蓄水池,其底面直径CD为12m,高CF为1.8米
素材2 如图3、图4,拟将在圆柱形蓄水池中心处建一能伸缩高度的喷水装置OP(OP⊥CD),要求水柱不能碰到图2中的水柱,也不能落在蓄水池外面.经调研,目前市场有两种喷水头均能喷射与图2中形状相同的抛物线.其中,甲喷水头以点P为最高点向四周喷射水柱(如图3),乙喷水头喷射水柱的最高点与点P的高度差为0.8m(如图4).
问题解决
任务1 确定水柱形状 在图2中以点O为坐标原点,水平方向为轴建立直角坐标系,求左边这条抛物线的函数表达式.
任务2 选择喷水装置甲,确定喷水装置的最高高度 若选择甲装置(图3),为防止水花溅出,当落水点G、M之间的距离满足时,OP不能再升高,求此时OP的最高高度.
任务3 选择喷水装置乙,拟定喷水装置的高度范围 若选择乙装置(图4),为了美观,要求OP喷出的水柱高度不低于5m,求喷水装置OP高度的变化范围.
14.在平面直角坐标系中,点(1,m)和(3,n)都在二次函数y=ax2+bx(a≠0,a,b是常数)的图象上.
(1)若m=n=﹣6,求该二次函数的表达式和函数图象的对称轴.
(2)若a=﹣1,m<n,求b的取值范围.
(3)已知点(﹣1,y1),(2,y2),(4,y3)也都在该二次函数图象上,若mn<0且a<0,试比较y1,y2,y3的大小,并说明理由.
15.如图,二次函数y=ax2+bx+3(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,C为顶点.
(1)请求出二次函数的表达式及图象的顶点C的坐标.
(2)若点E为抛物线对称轴左侧一点,过点E作x轴平行线交对称轴于点D,若ED=m,试用m的代数式表示CD.
(3)连结EC,过点C作CF⊥EC交抛物线于点F,过点F作x轴的平行线交对称轴于点G,证明:GF DE=1.
16.已知二次函数的图象经过原点O和点A(8+t,0),其中t≥0.
(1)当t=0时.
①求y关于x的函数表达式,并求出当x为何值时,y有最大值,最大值为多少?
②当x=m和x=n时(m≠n),函数值相等,求m,n之间的关系式.
(2)当t>0时,在0≤x≤8范围内,y是否存在最大值18?若存在,求出相应的t和x的值,若不存在,请说明理由.
答案与解析
押题方向:二次函数应用及综合问题
2023年浙江真题 考点 命题趋势
2023年湖州卷第21题 二次函数的应用 从近几年浙江各地中考来看,解答题中二次函数考查内容主要是二次函数的实际应用、二次函数综合,其中二次函数的综合题经常以压轴题出现,试题的整体难度比较高,预计2024年浙江卷还将重视二次函数综合问题的考查。
2023年湖州卷、衢州卷、绍兴卷、舟山、嘉兴卷、丽水卷第23题、杭州卷第22题、金华卷第24题 二次函数的综合
1.(2023 杭州)设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
【点拨】(1)①利用待定系数法即可求得;
②利用二次函数的性质得出结论;
(2)根据题意m≤0,由﹣=1,得出b=﹣2a,则二次函数为y=ax2﹣2ax+1,得出m=a+2a+1≤0,解得a≤﹣.
【解析】解:(1)①由题意得,
解得,
∴二次函数的表达式是y=x2﹣2x+1;
②∵y=x2﹣2x+1=(x﹣1)2,
∴抛物线开口向上,对称轴为直线x=1,
∴当x<1时,y随x的增大而减小;
(2)∵x=0和x=2时的函数值都是1,
∴抛物线的对称轴为直线x=﹣=1,
∴(1,n)是顶点,(﹣1,m)和(3,p)关于对称轴对称,
若在m,n,p这三个实数中,只有一个是正数,则抛物线必须开口向下,且m≤0,
∵﹣=1,
∴b=﹣2a,
∴二次函数为y=ax2﹣2ax+1,
∴m=a+2a+1≤0,
∴a≤﹣.
【点睛】本题考查了二次函数的图象与系数的关系,待定系数法求二次函数的解析式,二次函数的性质,二次函数图象上点的坐标特征,能够明确题意得出m=a+2a+1<0是解题的关键.
2.(2023 丽水)已知点(﹣m,0)和(3m,0)在二次函数y=ax2+bx+3(a,b是常数,a≠0)的图象上.
(1)当m=﹣1时,求a和b的值;
(2)若二次函数的图象经过点A(n,3)且点A不在坐标轴上,当﹣2<m<﹣1时,求n的取值范围;
【点拨】(1)当m=﹣1时,二次函数y=ax2+bx+3图象过点(1,0)和(﹣3,0),用待定系数法可得a的值是﹣1,b的值是﹣2;
(2)y=ax2+bx+3图象过点(﹣m,0)和(3m,0),可知抛物线的对称轴为直线x=m,而y=ax2+bx+3的图象过点A(n,3),(0,3),且点A不在坐标轴上,可得m=,根据﹣2<m<﹣1,即得﹣4<n<﹣2;
(3)由抛物线过(﹣m,0),(3m,0),可得﹣=m,b=﹣2am,把 (﹣m,0),(3m,0)代入y=ax2+bx+3变形可得am2+1=0,故b2+4a=(﹣2am)2+4a=4a(am2+1)=4a×0=0.
【解析】(1)解:当m=﹣1时,二次函数y=ax2+bx+3图象过点(1,0)和(﹣3,0),
∴,
∴解得,
∴a的值是﹣1,b的值是﹣2;
(2)解:∵y=ax2+bx+3图象过点(﹣m,0)和(3m,0),
∴抛物线的对称轴为直线x=m,
∵y=ax2+bx+3的图象过点A(n,3),(0,3),且点A不在坐标轴上,
∴由图象的对称性得n=2m,
∴m=,
∵﹣2<m<﹣1,
∴﹣2<<﹣1,
∴﹣4<n<﹣2;
(3)证明:∵抛物线过(﹣m,0),(3m,0),
∴抛物线对称轴为直线x==m,
∴﹣=m,
∴b=﹣2am,
把(﹣m,0),(3m,0)代入y=ax2+bx+3得:
,
①×3+②得:12am2+12=0,
∴am2+1=0,
∴b2+4a=(﹣2am)2+4a=4a(am2+1)=4a×0=0.
【点睛】本题考查二次函数图象上点坐标的特征,涉及待定系数法,不等式,方程组等知识,解题的关键是整体思想的应用.
3.(2023 宁波)如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).
(1)求该二次函数的表达式及图象的顶点坐标.
(2)当y≤﹣2时,请根据图象直接写出x的取值范围.
【点拨】(1)用待定系数法求出函数表达式,配成顶点式即可得顶点坐标;
(2)求出A关于对称轴的对称点坐标,由图象直接可得答案.
【解析】解:(1)把A(1,﹣2)和B(0,﹣5)代入y=x2+bx+c得:
,
解得,
∴二次函数的表达式为y=x2+2x﹣5,
∵y=x2+2x﹣5=(x+1)2﹣6,
∴顶点坐标为(﹣1,﹣6);
(2)如图:
∵点A(1,﹣2)关于对称轴直线x=﹣1的对称点C(﹣3,﹣2),
∴当y≤﹣2时,x的范围是﹣3≤x≤1.
【点睛】本题考查二次函数图象及性质,解题的关键是掌握待定系数法,求出函数表达式.
4.(2023 绍兴)已知二次函数y=﹣x2+bx+c.
(1)当b=4,c=3时,
①求该函数图象的顶点坐标;
②当﹣1≤x≤3时,求y的取值范围;
(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.
【点拨】(1)先把解析式进行配方,再求顶点;
(2)根据函数的增减性求解;
(3)根据函数的图象和系数的关系,结合图象求解.
【解析】解:(1)①∵b=4,c=3 时,
∴y=﹣x2+4x+3=﹣(x﹣2)2+7,
∴顶点坐标为(2,7).
②∵﹣1≤x≤3中含有顶点(2,7),
∴当 x=2 时,y有最大值7,
∵2﹣(﹣1)>3﹣2,
∴当x=﹣1 时,y有最小值为:﹣2,
∴当﹣1≤x≤3时,﹣2≤y≤7.
(2)∵x≤0时,y的最大值为2;x>0时,y的最大值为3,
∴抛物线的对称轴 在y轴的右侧,
∴b>0,
∵抛物线开口向下,x≤0时,y的最大值为2,
∴c=2,
又∵,
∴b=±2,
∵b>0,
∴b=2.
∴二次函数的表达式为 y=﹣x2+2x+2.
【点睛】本题考查了二次函数的性质,掌握数形结合思想是解题的关键.
5.(2023 湖州)某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量y(千克)与销售价格x(元/千克)(30≤x<60)存在一次函数关系,部分数据如表所示:
销售价格x(元/千克) 50 40
日销售量y(千克) 100 200
(1)试求出y关于x的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为W元,如果不考虑其他因素,求当销售价格x为多少时,日销售利润W最大?最大的日销售利润是多少元?
【点拨】(1)设y与x之间的函数关系式为y=kx+b,由表中数据即可得出结论;
(2)根据每日总利润=每千克利润×销售量列出函数解析式,根据函数的性质求最值即可.
【解析】解:(1)设y关于x的函数表达式为y=kx+b(k≠0).
将x=50,y=100和x=40,y=200分别代入,得:,
解得:,
∴y关于x的函数表达式是:y=﹣10x+600.
(2)W=(x﹣30)(﹣10x+600)=﹣10x2+900x﹣18000.
当x=﹣=45时,在30≤x<60的范围内,W取到最大值,最大值是2250.
答:销售价格为每千克45元时,日销售利润最大,最大日销售利润是2250元.
【点睛】本题考查一次函数、二次函数的应用,关键是根据等量关系写出函数解析式.
6.(2023 温州)一次足球训练中,小明从球门正前方8m的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素);
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25m处?
【点拨】(1)求出抛物线的顶点坐标为(2,3),设抛物线为 y=a(x﹣2)2+3,用待定系数法可得y=﹣(x﹣2)2+3;当x=0时,y=﹣×4+3=>2.44,知球不能射进球门.
(2)设小明带球向正后方移动m米,则移动后的抛物线为y=﹣(x﹣2﹣m)2+3,把点(0,2.25)代入得 m=﹣5(舍去)或m=1,即知当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方2.25m处.
【解析】解:(1)∵8﹣6=2,
∴抛物线的顶点坐标为(2,3),
设抛物线为 y=a(x﹣2)2+3,
把点A(8,0)代入得:36a+3=0,
解得a=﹣,
∴抛物线的函数表达式为y=﹣(x﹣2)2+3;
当x=0时,y=﹣×4+3=>2.44,
∴球不能射进球门.
(2)设小明带球向正后方移动m米,则移动后的抛物线为y=﹣(x﹣2﹣m)2+3,
把点(0,2.25)代入得:2.25=﹣(0﹣2﹣m)2+3,
解得 m=﹣5(舍去)或m=1,
∴当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方2.25m处.
【点睛】本题考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
7.(2023 湖州)如图1,在平面直角坐标系xOy中,二次函数y=x2﹣4x+c的图象与y轴的交点坐标为(0,5),图象的顶点为M.矩形ABCD的顶点D与原点O重合,顶点A,C分别在x轴,y轴上,顶点B的坐标为(1,5).
(1)求c的值及顶点M的坐标.
(2)如图2,将矩形ABCD沿x轴正方向平移t个单位(0<t<3)得到对应的矩形A′B′C′D′.已知边C′D′,A′B′分别与函数y=x2﹣4x+c的图象交于点P,Q,连接PQ,过点P作PG⊥A′B′于点G.
①当t=2时,求QG的长;
②当点G与点Q不重合时,是否存在这样的t,使得△PGQ的面积为1?若存在,求出此时t的值;若不存在,请说明理由.
【点拨】(1)运用待定系数法将(0,5)代入y=x2﹣4x+c,即可求得c的值,再利用配方法将抛物线的解析式化为顶点式或运用顶点公式即可求得答案;
(2)①当t=2时,D′,A′的坐标分别是(2,0),(3,0).进而可求得点P、Q的纵坐标,利用QG=yQ﹣yG,即可求得答案;
②根据题意,得:P(t,t2﹣4t+5),Q(t+1,t2﹣2t+2),G(t+1,t2﹣4t+5),分两种情况:当点G在点Q的上方时,当点G在点Q的下方时,分别求得t的值即可.
【解析】解 (1)∵二次函数y=x2﹣4x+c的图象与y轴的交点坐标为(0,5),
∴c=5,
∴y=x2﹣4x+5=(x﹣2)2+1,
∴顶点M的坐标是(2,1).
(2)①如图1,∵A在x轴上,B的坐标为(1,5),
∴点A的坐标是(1,0).
当t=2时,D′,A′的坐标分别是(2,0),(3,0).
当x=3时,y=32﹣4×3+5=2,即点Q的纵坐标是2.
当x=2时,y=1,即点P的纵坐标是1.
∵PG⊥A′B′,
∴点G的纵坐标是1,
∴QG=2﹣1=1.
②存在.理由如下:
∵△PGQ的面积为1,PG=1,
∴QG=2.
根据题意,得:P(t,t2﹣4t+5),Q(t+1,t2﹣2t+2),
∴G(t+1,t2﹣4t+5),
如图2,当点G在点Q的上方时,
QG=t2﹣4t+5﹣(t2﹣2t+2)=3﹣2t=2,
此时(在0<t<3的范围内).
如图3,当点G在点Q的下方时,
QG=t2﹣2t+2﹣(t2﹣4t+5)=2t﹣3=2,
此时(在0<t<3的范围内).
综上所述,存在t,使得△PGQ的面积为1,此时t的值为或.
【点睛】本题是二次函数综合题,考查了待定系数法,抛物线的顶点,平移变换的性质,三角形面积等,运用数形结合思想和分类讨论思想是解题关键.
8.(2023 金华)如图,直线y=与x轴,y轴分别交于点A,B,抛物线的顶点P在直线AB上,与x轴的交点为C,D,其中点C的坐标为(2,0),直线BC与直线PD相交于点E.
(1)如图2,若抛物线经过原点O.
①求该抛物线的函数表达式;
②求的值.
(2)连结PC,∠CPE与∠BAO能否相等?若能,求符合条件的点P的横坐标;若不能,试说明理由.
【点拨】(1)①由抛物线经过原点O(0,0)、C(2,0),可得抛物线的顶点P(1,),利用待定系数法可得抛物线的函数表达式为y=﹣x2+3x;
②先求出A(﹣2,0),B(0,),运用待定系数法可得直线OP的解析式为y=x,过点B作BF∥x轴交OP于点F,F(,),可得BF=,再由BF∥OC,得出△BEF∽△CEO,进而可得===;
(2)分四种情形,分别作出图形求解即可.
【解析】解:(1)①∵抛物线经过原点O(0,0)、C(2,0),
∴对称轴为直线x=1,
当x=1时,y=×1+=,
∴抛物线的顶点P(1,),
设抛物线的解析式为y=a(x﹣1)2+,把C(2,0)代入,得a+=0,
解得:a=﹣,
∴y=﹣(x﹣1)2+=﹣x2+3x,
∴该抛物线的函数表达式为y=﹣x2+3x;
②∵直线y=与x轴,y轴分别交于点A,B,
∴A(﹣2,0),B(0,),
设直线OP的解析式为y=kx,把P(1,)代入,得:k=,
∴直线OP的解析式为y=x,
如图,过点B作BF∥x轴交OP于点F,则点F的纵坐标与点B的纵坐标相同,
∴=x,
解得:x=,
∴F(,),
∴BF=,
∵BF∥OC,
∴△BEF∽△CEO,
∴===,
∴的值为.
(2)设点P的横坐标为t,
①如图2﹣1,当t>2,存在∠CPE=∠BAO,
设∠CPE=∠BAO=α,∠APC=β,则∠APD=α+β,
∵∠PCD=∠PAO+∠APC=α+β,
∵PC=PD,
∴∠PDC=∠PCD=∠APD,
∴AP=AD=2t,
过点P作PF⊥x轴于点F,则AF=t+2,
在Rt△APF中,cos∠BAO==,
∴=,
∴t=6.
②如图2﹣2中,当0<t≤2时,存在∠CPE=∠BAO.
过点P作PF⊥x轴于点F,
同法cos∠BAO==,
∴=,
∴t=.
③如图2﹣3中,当﹣2<t≤0时,存在∠CPE=∠BAO=α,
∵PC=PD,
∴∠CPE=α,
∴∠BAO﹣∠PDC=α,
∴∠APD=∠PDA,
∴AD=AP=﹣2t,
同法cos∠BAO==,
∴=,
∴t=﹣.
④当t≤﹣2时,同法cos∠BAO==,
=,
∴t=﹣
综上所述.点P的横坐标为6或﹣或或﹣.
【点睛】本题是二次函数综合题,考查了待定系数法求函数解析式,一次函数与二次函数综合运用,勾股定理,等腰三角形性质,相似三角形的判定和性质等,添加辅助线构造相似三角形是解题关键.
9.(2023 浙江)在二次函数y=x2﹣2tx+3(t>0)中.
(1)若它的图象过点(2,1),则t的值为多少?
(2)当0≤x≤3时,y的最小值为﹣2,求出t的值;
(3)如果A(m﹣2,a),B(4,b),C(m,a)都在这个二次函数的图象上,且a<b<3.求m的取值范围.
【点拨】(1)将(2,1)代入y=x2﹣2tx+3即可得t=;
(2)抛物线y=x2﹣2tx+3对称轴为 x=t.若0<t≤3,有t2﹣2t2+3=﹣2,若t>3,有9﹣6t+3=﹣2,解方程并检验可得t的值为;
(3)根据A(m﹣2,a),C(m,a)都在这个二次函数的图象上,可得二次函数y=x2﹣2tx+3的对称轴直线x=t即为直线x==m﹣1,由t>0,得m>1,因m﹣2<m,知A在对称轴左侧,C在对称轴右侧,抛物线y=x2﹣2tx+3与y轴交点为(0,3),其关于对称轴直线x=m﹣1的对称点为(2m﹣2,3),由b<3,知4<2m﹣2,m>3;①当A(m﹣2,a),B(4,b)都在对称轴左侧时,y随x的增大而减小,有4<m﹣2,可得m满足的条件为m>6;②当A(m﹣2,a)在对称轴左侧,B(4,b)在对称轴右侧时,B(4,b)到对称轴直线x=m﹣1距离大于A(m﹣2,a)到对称轴直线x=m﹣1的距离,故4﹣(m﹣1)>m﹣1﹣(m﹣2),得:m<4,m满足的条件是3<m<4.
【解析】解:(1)将(2,1)代入y=x2﹣2tx+3得:
1=4﹣4t+3,
解得:t=;
(2)抛物线y=x2﹣2tx+3对称轴为 x=t.
若0<t≤3,当x=t时函数取最小值,
∴t2﹣2t2+3=﹣2,
解得t=;
若t>3,当x=3时函数取最小值,
∴9﹣6t+3=﹣2,
解得 (不符合题意,舍去);
综上所述,t的值为;
(3)∵A(m﹣2,a),C(m,a)都在这个二次函数的图象上,
∴二次函数y=x2﹣2tx+3的对称轴直线x=t即为直线x==m﹣1,
∴t=m﹣1,
∵t>0,
∴m﹣1>0,
解得m>1,
∵m﹣2<m,
∴A在对称轴左侧,C在对称轴右侧,
在y=x2﹣2tx+3中,令x=0得y=3,
∴抛物线y=x2﹣2tx+3与y轴交点为(0,3),
∴(0,3)关于对称轴直线x=m﹣1的对称点为(2m﹣2,3),
∵b<3,
∴4<2m﹣2,
解得m>3;
①当A(m﹣2,a),B(4,b)都在对称轴左侧时,
∵y随x的增大而减小,且a<b,
∴4<m﹣2,
解得m>6,
此时m满足的条件为m>6;
②当A(m﹣2,a)在对称轴左侧,B(4,b)在对称轴右侧时,
∵a<b,
∴B(4,b)到对称轴直线x=m﹣1距离大于A(m﹣2,a)到对称轴直线x=m﹣1的距离,
∴4﹣(m﹣1)>m﹣1﹣(m﹣2),
解得:m<4,
此时m满足的条件是3<m<4,
综上所述,3<m<4或m>6.
【点睛】本题考查二次函数的综合应用,涉及函数图象上点坐标的特征,解题的关键是分类讨论思想的应用.
10.(2023 衢州)某龙舟队进行500米直道训练,全程分为启航,途中和冲刺三个阶段.图1,图2分别表示启航阶段和途中阶段龙舟划行总路程s(m)与时间t(s)的近似函数图象.启航阶段的函数表达式为s=kt2(k≠0);途中阶段匀速划行,函数图象为线段;在冲刺阶段,龙舟先加速后匀速划行,加速期龙舟划行总路程s(m)与时间t(s)的函数表达式为s=k(t﹣70)2+h(k≠0).
(1)求出启航阶段s(m)关于t(s)的函数表达式(写出自变量的取值范围).
(2)已知途中阶段龙舟速度为5m/s.
①当t=90s时,求出此时龙舟划行的总路程.
②在距离终点125米处设置计时点,龙舟到达时,t≤85.20s视为达标.请说明该龙舟队能否达标.
(3)冲刺阶段,加速期龙舟用时1s将速度从5m/s提高到5.25m/s,之后保持匀速划行至终点.求该龙舟队完成训练所需时间(精确到0.01s).
【点拨】(1)把A(20,50)代入s=kt2 得出k的值,则可得出答案;
(2)①设s=5t+b,把(20,50)代入,得出50=5×20+b,求得b=﹣50,当t=90时,求出s=400,则可得出答案;
②把s=375代入s=5t﹣50,求得t=85,则可得出答案;
(3)由(1)可知k=,把(90,400)代入s=,求得h=350.求出s=405.125,则可得出答案.
【解析】解:(1)把A(20,50)代入s=kt2 得50=400k,
解得,
∴启航阶段总路程s关于时间t的函数表达式为s=(0<t≤20);
(2)①设s=5t+b,把(20,50)代入,得50=5×20+b,
解得b=﹣50,
∴s=5t﹣50.
当t=90时,s=450﹣50=400.
∴当t=90s时,龙舟划行的总路程为400m.
②500﹣125=375,
把s=375代入s=5t﹣50,
得t=85.
∵85<85.20,
∴该龙舟队能达标.
(3)加速期:由(1)可知k=,
把(90,400)代入s=,
得h=350.
∴函数表达式为s=,
把t=91代入s=,
解得s=405.125.
∴(500﹣405.125)÷5.25≈18.07(s),
∴90+1+18.07=109.07(s).
答:该龙舟队完成训练所需时间为109,07s.
【点睛】本题是二次函数综合题,考查了二次函数的应用,一次函数的性质,二次函数图象上点的坐标特征,待定系数法,根据条件准确得到表达式是解题关键.
11.(2024 嘉善县一模)已知二次函数y=ax2+bx+c(a≠0),且a>b>c,a+b+c=0.
(1)当b=0时,求方程ax2+bx+c=0的根;
(2)已知该二次函数的对称轴为x=m,求证:;
(3)已知该二次函数的图象与x轴,y轴分别交于A(x1,0),B(x2,0),C(0,c)三点(A在B的左侧),且x1+4x2=0,若△ABC为直角三角形,求该二次函数表达式.
【点拨】(1)当b=0时,方程为:ax2+c=0,即可求解;
(2)证明a>0且c<0,即可求解;
(3)若△ABC为直角三角形,则只存在∠ACB为直角,即可求解.
【解析】(1)解:∵a>b>c,a+b+c=0,
则a>0且c<0,
当b=0时,方程为:ax2+c=0,
解得:x=±;
(2)证明:由(1)知,a>0且c<0,
则a+b=﹣c>0,
即a+b>0,
则﹣<1,
即﹣<,
∴;
(3)解:∵a>0且c<0,且x1+4x2=0,
解:由(1)知,抛物线的表达式为:y=ax2+bx+(﹣a﹣b),
则x1+x2=﹣且x1x2=﹣,
将x1+4x2=0代入上式两式得:4x2==1+=1+3x2,
解得:x2=1,则x1=﹣4,
即点A、B的坐标分别为:(﹣4,0)、(1,0),
则可大致画出函数的图象如下:
若△ABC为直角三角形,
则只存在∠ACB为直角,
则∵∠ACO+∠OCB=90°,∠OCB+∠OBC=90°,
∴∠ACO=∠OBC,
∴tan∠ACO=tan∠OBC,
则OC2=OA×OB,
即CO2=1×4=4,
解得:CO=2,
则点C(0,﹣2),
由题意得,抛物线的表达式为:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),
则﹣4a=﹣2,
解得:a=,
则抛物线的表达式为:y=x2﹣x﹣2.
【点睛】本题考查的是二次函数综合运用,涉及到解直角三角形、直角三角形的性质等熟悉二次函数的图象和性质是解题的关键.
1.二次函数的应用:应用待定系数法,根据条件准确得到表达式是解题关键.
2.二次函数的综合问题:熟练掌握待定系数法求函数的解析式,一次函数的图象与性质,二次函数的图象与性质,函数图象上点的特征是解题的关键.
3.要重视数形结合在解决二次函数综合问题中的作用.
1.在平面直角坐标系中,设二次函数y=ax2+bx﹣4a(a,b是常数,a≠0).
(1)判断该函数图象与x轴的交点个数,并说明理由;
(2)若该函数图象的对称轴为直线x=2,A(x1,m),B(x2,m)为该函数图象上的任意两点,其中x1<x2,求当x1,x2为何值时,m=8a;
(3)若该函数图象的顶点在第二象限,且过点(1,2),当a<b时求3a+b的取值范围.
【点拨】(1)依据题意,求出Δ=b2﹣4a(﹣4a)=b2+16a2,进而结合a≠0可以判断Δ>0,即可求解;
(2)依据题意,也有对称轴为直线x=2,可得b=﹣4a,从而y=ax2+bx﹣4a=ax2﹣4ax﹣4a,当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,然后计算即可求解;
(3)依据题意,由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,则抛物线开口向下,即a<0,进而求解.
【解析】解:(1)由题意得,Δ=b2﹣4a(﹣4a)=b2+16a2,
又a≠0,
∴a2>0.
∴16a2>0.
又对于任意的b都有b2≥0,
∴Δ=b2+16a2>0.
∴函数图象与x轴的交点个数为2.
(2)∵x=2=﹣,
∴b=﹣4a.
∴抛物线表达式为y=ax2+bx﹣4a=ax2﹣4ax﹣4a,
当y1=y2=8a时,即y=ax2﹣4ax﹣4a=8a,
解得x=6或﹣2,
则x1=﹣2,x2=6.
(3)将(1,2)代入抛物线表达式得:2=a+b﹣4a,则b=3a+2,
∵a<b,故a<3a+2,
∴解得a>﹣1.
∴抛物线的表达式为y=ax2+(3a+2)x﹣4a,
由(1)知,函数图象与x轴的交点个数为2且图象的顶点在第二象限,
∴抛物线开口向下,即a<0.
∴函数的对称轴x=﹣=﹣﹣<0,
解得a<﹣,
∴﹣1<a<﹣.
∴﹣3<3a<﹣2.
故﹣1<3a+2<0,即﹣1<b<0.
∴﹣4<3a+b<﹣2.
∴3a+b的取值范围:﹣4<3a+b<﹣2.
【点睛】本题主要考查的是抛物线与x轴的交点、函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.
2.在二次函数y=﹣x2+ax+1中(a≠0).
(1)当a=2时,
①求该二次函数图象的顶点坐标;
②当0≤x≤3时,求y的取值范围;
(2)若A(a﹣2,b),B(a,c)两点都在这个二次函数的图象上,且b<c,求a的取值范围.
【点拨】(1)①把解析式化成顶点式即可求得;
②根据二次函数的性质,可以得到当0<x<3时,y的取值范围;
(2)根据抛物线的对称性及增减性即可解决问题.
【解析】解:(1)①把 a=2 代入得 y=﹣x2+2x+1=﹣(x﹣1)2+2,
∴抛物线的顶点坐标为(1,2);
②∵y=﹣x2+2x+1的开口向下,对称轴为直线x=1,
∴当0≤x≤1时,y随x的增大而增大,当1≤x≤3时,y随x的增大而减小,
∴当x=1时,y有最大值2.
∵当x=0时,y=1;当x=3时,y=﹣2
∴当0≤x≤3时,﹣2≤y≤2;
(2)抛物线的对称轴为直线 ,
①当 ,即0≤a≤4时,点B到对称轴的距离小于点A到对称轴的距离,
∴,解得a<2,
∴0≤a<2
②当 ,即a<0时,点B到对称轴的距离小于点A到对称轴的距离,
∴ 成立,
∴a<0
③对称轴在点A左侧不合题意,舍去,
综上所述,a<2.
【点睛】本题考查二次函数图象与系数的关系,二次函数图象上点的坐标特征及二次函数的性质,熟知二次函数的图象和性质及巧用分类讨论的数学思想是解题的关键.
3.已知二次函数y=x2﹣2kx+k﹣2的图象过点(5,5).
(1)求二次函数的表达式.
(2)若A(x1,y1)和B(x2,y2)都是二次函数图象上的点,且x1+2x2=2,求y1+y2的最小值.
(3)若点P(a,n)和Q(b,n+2)都在二次函数的图象上,且a<b.对于某一个实数n,若b﹣a的最小值为1,则b﹣a的最大值为多少?
【点拨】(1)利用待定系数法即可求解;
(2)根据图象上点的坐标特征得出y1+y2=﹣4x1+﹣4x2,由x1+2x2=2可知x1=2﹣2x2,即可求得y1+y2=﹣4x1+﹣4x2=5(x2﹣)2﹣,利用二次函数的性质即可求得最小值;
(3)由题意可知当点P(a,n)和Q(b,n+2)在对称轴的同侧时b﹣a的值最小,当点P(a,n)和Q(b,n+2)在异侧是b﹣a的值最大,据此求解即可.
【解析】解:(1)∵二次函数y=x2﹣2kx+k﹣2的图象过点(5,5),
∴5=25﹣10k+k﹣2,
∴k=2,
∴二次函数的表达式为y=x2﹣4x;
(2)∵A(x1,y1)和B(x2,y2)都是二次函数图象上的点,
∴y1=﹣4x1,y2=﹣4x2,
∴y1+y2=﹣4x1+﹣4x2,
∵x1+2x2=2,
∴x1=2﹣2x2,
∴y1+y2
=﹣4x1+﹣4x2
=(2﹣2x2)2﹣4(2﹣2x2)+﹣4x2
=5﹣4x2﹣4
=5(x2﹣)2﹣,
∵5>0,
∴y1+y2的最小值是﹣;
(3)∵抛物线y=x2﹣4x=(x﹣2)2﹣4,
∴t图象开口向上,对称轴为直线x=2,
∵点P(a,n)和Q(b,n+2)都在二次函数的图象上,且a<b.对于某一个实数n,若b﹣a的最小值为1,
∴点P(a,n)和Q(b,n+2)在对称轴的右侧,此时b﹣a=1,则b=a+1,
∴a2﹣4a=n①,(a+1)2﹣4(a+1)=n+2②,
②﹣①得a=,
∴b=a+1=,
∴此时点P(,n)和Q(,n+2),
当点P是点(,n)的对称点时,则b﹣a的值最大,
∵对称轴为直线x=2,
∴点(,n)的对称点为(,n),
∴此时a=,
∴b﹣a的最大值为:﹣=2.
【点睛】本题考查了待定系数法求二次函数的解析式,二次函数的性质,二次函数的最值,掌握二次函数的性质是解题的关键.
4.定义:对于y关于x的函数,函数在x1≤x≤x2(x1<x2)范围内的最大值,记作M[x1,x2].
如函数y=2x,在﹣1≤x≤3范围内,该函数的最大值是6,即M[﹣1,3]=6.
请根据以上信息,完成以下问题:
已知函数y=(a﹣1)x2﹣4x+a2﹣1(a为常数).
(1)若a=2.
①直接写出该函数的表达式,并求M[1,4]的值;
②已知,求p的值.
(2)若该函数的图象经过点(0,0),且M[﹣3,k]=k,求k的值.
【点拨】(1)①将a值代入运算即可,利用新定义的规定计算即可;
②令y=3,求得x值,再利用新定义的规定解答即可;
(2)利用待定系数法求得a值,再利用分类讨论的方法,依据新定义的规定列出关于k的方程解答即可.
【解析】解:(1)①∵a=2,
∴y=x2﹣4x+3.
∵[1,4],
∴1≤x≤4.
∴当x=4时,y=x2﹣4x+3=3,取得最大值,
∴M[1,4]=3;
②∵,
∴当p≤x≤时,函数y取得最大值3,
令y=3,则x2﹣4x+3=3,
∴x=0或x=4.
∴p=0.
(2)∵该函数的图象经过点(0,0),
∴a2﹣1=0,
∴a=±1.
当a=1时,y=﹣4x,
∵M[﹣3,k]=k,
∴k=﹣4×(﹣3)=12,
∴k=12.
当a=﹣1时,y=﹣2x2﹣4x.
∵y=﹣2(x+1)2+2,
∴当x=﹣1时,y取得最大值为2,
∵M[﹣3,k]=k,
∴﹣2k2﹣4k=k,
∴k=0(不合题意,舍去)或k=﹣.
∵当a=﹣1时,y=﹣2x2﹣4x.
∵y=﹣2(x+1)2+2,
∴当x=﹣1时,y取得最大值为2,
∴k=2.
当﹣3≤x≤2时,函数的最大值为2,
∴k=2.
综上,k的值为12或k=﹣或k=2.
【点睛】本题主要考查了二次函数的解析式,一次函数的性质,待定系数法,二次函数图象的性质,本题是新定义型,正确理解新定义的规定并熟练运用是解题的关键.
5.设二次函数y=ax2+bx+1(a≠0,b是常数),已知函数值y和自变量x的部分对应取值如表所示:
x … ﹣1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=0时,求二次函数的表达式;
(2)当﹣1≤x≤3时,y有最小值为,求a的值;
(3)若a<﹣3,求证:n﹣m﹣p>20.
【点拨】(1)利用待定系数法解答即可;
(2)利用抛物线的对称性得出抛物线的对称轴为直线x=1,利用二次函数的性质得到当x=1时,函数y取得最小值,再利用待定系数法解答即可;
(3)利用抛物线的对称轴为直线x=1,得到b=﹣2a,则y=ax2﹣2ax+1,利用表格求得m,np的值,并计算出n﹣m﹣p=﹣7a﹣1,再利用不等式的性质解答即可得出结论.
【解析】(1)解:当m=0时,抛物线y=ax2+bx+1经过(﹣1,0),(0,1),(2,1)三点,
∴,
∴,
∴二次函数的表达式为y=﹣x+1;
(2)解:∵抛物线y=ax2+bx+1经过(0,1),(2,1)两点,
∴当x=0或x=2时,y=1,
∴抛物线的对称轴为直线x=1,
∴y=ax2﹣2ax+1,
∵当﹣1≤x≤3时,y有最小值为,
∴如果a>0,当x=1时,函数y取得最小值,
∴,
∴.
∴a的值为;
如果a<0,则x=﹣1或x=3时,函数y取得最小值,
∴a×(﹣1)2﹣2a×(﹣1)+1=,
∴a=﹣.
综上,a的值为或﹣.
(3)证明:由(2)知:抛物线的对称轴为直线x=1,
∴=1,
∴b=﹣2a.
∴y=ax2﹣2ax+1,
∴m=a×(﹣1)2﹣2a×(﹣1)+1=3a+1,n=a﹣2a+1=﹣a+1,p=m=3a+1,
∴n﹣m﹣p=﹣a+1﹣(3a+1)﹣(3a+1)=﹣7a﹣1.
∵a<﹣3,
∴﹣7a>21,
∴﹣7a﹣1>20.
即:n﹣m﹣p>20.
【点睛】本题主要考查了二次函数的性质,待定系数法,抛物线上点的坐标的特征,二次函数的极值,熟练掌握二次函数的性质和待定系数法是解题的关键.
6.(2024 浙江模拟)已知点A(m,p),B(3,q),C(m+2,p)都在二次函数y=2x2+bx+4的图象上.
(1)若m=1,求该二次函数的表达式;
(2)求p+q的最大值;
(3)若p<q<4,求m的取值范围.
【点拨】(1)当m=1时,根据二次函数的对称轴为直线x=﹣==m+1求出b即可;
(2)根据﹣=m+1得出b=﹣4(m+1),然后求出p+q关于m的二次函数解析式,根据函数的性质求最值;
(3)根据p<q<4以及二次函数的性质求出m的取值范围.
【解析】解:(1)根据题意得,二次函数的对称轴为直线x=﹣==m+1,
当m=1时,﹣=2,
∴b=﹣8,
∴二次函数的表达式为y=2x2﹣8x+4;
(2)∵﹣=m+1,
∴b=﹣4(m+1),
把A,B坐标分别代入y=2x2+bx+4得,
p=2m2﹣4(m+1)m+4=﹣2m2﹣4m+4,
q=18﹣4(m+1)×3+4=﹣12m+10,
∴p+q=﹣2m2﹣4m+4﹣12m+10=﹣2m2﹣16m+14=﹣2(m﹣4)2+46,
∵﹣2<0,
∴m=4时,p+q最大值为46;
(3)∵p<q,
∴m>3或m+2<3,
∵q<4,
∴﹣12m+10<4,
解得m>,
∴m的取值范围为<m<1或m>3.
【点睛】本题考查待定系数法求函数解析式、二次函数的最值以及二次函数的性质,关键是利用二次函数的性质解答.
7.已知二次函数y1=ax(x+b)(a≠0)和一次函数y2=ax+m.
(1)若二次函数y1的图象过点(1,0)和(2,2),求二次函数的表达式.
(2)若一次函数y2与二次函数y1的图象交于x轴上同一点A,且A不是原点.
①求证:m=ab;
②若二次函数y1与一次函数y2的另一个交点B为y1的顶点,求b的值.
【点拨】(1)利用待定系数法解答即可;
(2)①令y=0,分别求得两个函数的图象与x轴的交点,依据已知条件列出关于a,b,m的等式,整理即可得出结论;
②利用配方法求得抛物线的顶点坐标,将坐标代入一次函数的解析式,再利用①的结论得到关于b的方程,解方程即可得出结论.
【解析】(1)解:∵二次函数y1的图象过(1,0),(2,2)点,
∴,
解得:,
∴二次函数的表达式为y=x2﹣x;
(2)①证明:令y1=0,则ax(x+b)=0,
解得:x=0或x=﹣b.
∴抛物线y1=ax(x+b)与x轴交于(0,0)(﹣b,0).
令y2=0,则ax+m=0,
∴x=﹣.
∴直线y2=ax+m与x轴交于(﹣,0),
∵若一次函数y2与二次函数y1的图象交于x轴上同一点,且这个点不是原点,
∴﹣=﹣b,
∴m=ab;
②解:∵y1=ax(x+b)=ax2+abx=a(x+)2﹣,
∴二次函数的顶点为(﹣,﹣).
∵两个函数图象的另一个交点为二次函数的顶点,
∴a (﹣)+m=﹣.
由①知:m=ab,
∴﹣+ab=﹣,
解得:b=0(不合题意,舍去)或b=﹣2.
∴若两个函数图象的另一个交点为二次函数的顶点,b的值为﹣2.
【点睛】本题主要考查了二次函数的图象与性质,一次函数的图象与性质,待定系数法,函数图象的交点,抛物线上点的坐标的特征,一次函数图象上点的坐标的特征,熟练掌握待定系数法是解题的关键.
8.(2024 宁波模拟)设一次函数y1=a(x+m)的图象与x轴交于点A,二次函数的图象与x轴交于A,B两个不同的点,设函数y=y1+y2.
(1)设点Q(0,q)在函数y的图象上,若q>c,求证:am>0.
(2)若函数y2,y的图象在x轴上截得的线段长分别为d1,d2,求d1,d2的数量关系式.
(3)若函数y1的图象分别与函数y2的图象、函数y的图象交于点E(x1,e),F(x2,f),且点E,F不同于点A,求x1﹣x2的值.
【点拨】(1)把y1与y2相加得y=ax2+(a+b)x+am+c,把点Q代入y,再计算即可.
(2)设A(t,0),代入y1得y1=a(x﹣t).设B(k,0),又A(t,0)得y2=ax2﹣(at+ak)x+atk,
故y=ax2+(a﹣at﹣ak)x+atk﹣at,设y2=ax2﹣(at+ak)x+atk两根为p、q,再计算即可.
(3)由(2)知y1=a(x﹣t),y2=a(x﹣t)(x﹣k),得a(x﹣t)=a(x﹣t)(x﹣k),计算得x1=k+1.
由y1=a(x﹣t),y=a(x﹣t)+ax2﹣(at+ak)x+atk,得a(x﹣t)=a(x﹣t)+ax2﹣(at+ak)x+atk,计算得x2=k.故x1﹣x2=k+1﹣k=1.
【解析】解:(1)∵y1=a(x+m),,
∴y=y1+y2=a(x+m)+ax2+bx+c=ax2+(a+b)x+am+c,
∵点Q(0,q)在函数y的图象上,
∴q=am+c,
即q﹣c=am,
∵q>c,
∴am>0.
(2)设A(t,0),代入y1=a(x+m)得:
0=a(t+m),
∵a≠0,
∴t+m=0,
∴m=﹣t,
y1=a(x﹣t).
设B(k,0),又A(t,0),
∴y2=a(x﹣t)(x﹣k)=ax2﹣(at+ak)x+atk,
∴y=a(x﹣t)+ax2﹣(at+ak)x+atk=ax2+(a﹣at﹣ak)x+atk﹣at,
设y2=ax2﹣(at+ak)x+atk两根为p、q,
∴p+q==t+k,pq==tk,
∴=(p﹣q)2=(p+q)2﹣4pq=(t+k)2﹣4tk=t2+k2﹣2tk,
即=t2+k2﹣2tk=(t﹣k)2,
∴d1=,
设y=ax2+(a﹣at﹣ak)x+atk﹣at两根为r、s,
∴r+s==k+t﹣1,rs==kt﹣t,
∴=(r﹣s)2=(r+s)2﹣4rs=(k+t﹣1)2﹣4(kt﹣t)=k2+t2﹣2tk﹣2k+2t+1,
∴﹣=|(t2+k2﹣2tk)﹣(k2+t2﹣2tk﹣2k+2t+1)|=|2(k﹣t)﹣1|=±2d1﹣1,
答:d1,d2的数量关系式是:﹣=±2d1﹣1.
(3)由(2)知y1=a(x﹣t),y2=a(x﹣t)(x﹣k),
得a(x﹣t)=a(x﹣t)(x﹣k),
∴a(x﹣t)(x﹣k)﹣a(x﹣t)=0,
∴a(x﹣t)(x﹣k﹣1)=0,
∴x=t,x=k+1,
即A(t,0),x1=k+1.
由y1=a(x﹣t),y=a(x﹣t)+ax2﹣(at+ak)x+atk,
得a(x﹣t)=a(x﹣t)+ax2﹣(at+ak)x+atk,
∴ax2﹣(at+ak)x+atk=0,
∴x2﹣(t+k)x+tk=0,
∴(x﹣t)(x﹣k)=0,
∴x=t,x=k,
即A(t,0),x2=k.
∴x1﹣x2=k+1﹣k=1.
【点睛】本题考查了抛物线的知识,掌握抛物线的性质是解题关键.
9.如图,小车从点A出发,沿与水平面成30°角光滑斜坡AB下滑,在下滑过程中小车速度逐渐增加,设小车出发点A离水平地面BE的高度为h,小车从点A滑行到最低点B所用的时间为t(秒),小车滑行到点B时的速度为v(厘米/秒).速度v与时间t满足关系:v=10t,高度h与时间t满足关系:(g≠0,g是常数),当小车出发点小车出发点A离水平地面BE的高度为20(厘米)时,小车从点A滑到最低点B需要2秒.
(1)当小车出发点A离水平地面BE的高度为45(厘米)时,小车滑到最低点B需要几秒钟?此时小车到达B点时的速度是多少?
(2)小车继续在粗糙的水平地面BE上滑行,设滑行的距离为s(厘米),小车从斜坡滑行到点B时速度为v(厘米/秒),小车在水平地面BE上滑行的时间为T(秒),若s与v,T之间满足以下关系:+vT(a≠0,a是常数),当v=20(厘米/秒)时,s=50(厘米),T=5(秒).如果把小车出发点A离水平地面BE的距离h提高到125厘米,那么当滑行到时间T=4秒时,小车在水平地面BE上滑行的距离为多少?
【点拨】(1)先根据已知条件求出g的值,求出高度h与时间t的函数解析式,再把h=45代入解析式求出t,再把t的值代入y=10t求出速度v;
(2)先把v=20,s=50,T=5代入+vT求出a的值,再根据h=125求出t,再求出v,然后求出s即可.
【解析】解:(1)当t=2,h=20时,20=g×22,
解得g=10,
∴h=×10t2=5t2;
∴当h=45时,5t2=45,
解得t=3或t=﹣3(舍去),
此时v=10×3=30(cm/s),
答:当小车出发点A离水平地面BE的高度为45(厘米)时,小车滑到最低点B需要3秒钟,此时小车到达B点时的速度是30厘米/秒;
(2)把v=20,s=50,T=5代入+vT,
则50=﹣a×52+20×5,
解得a=4,
∴s=﹣2T2+vT,
当h=125时,5t2=125,
解得t=5或t=﹣5(舍去),
∴v=10×5=50(cm/s),
∴s=﹣2×42+50×4=168(cm).
答:小车在水平地面BE上滑行的距离为168cm.
【点睛】本题考查二次函数的应用,关键是待定系数法求函数解析式.
10.(2024 北仑区一模)周末,小明和同学们一起去长江路地铁站坐地铁.在等车的过程中,他惊叹于地铁每次都能精准的停靠在停止线上.为什么每次地铁停靠都那么准呢?里面一定包含着数学知识!通过工作人员帮助,小明获得了地铁刹车开始的时间t与地铁到停止线的距离S之间的表格信息:
t(秒) 0 4 8 12 16 20 24 …
S(米) 256 196 144 100 64 36 16 …
当小明拿到这些数据时,他作了如下的思考:
(1)依据数学经验,小明需要将这些数据绘制在平面直角坐标系中,并用平滑的曲线进行连线,形成数据所生成的图象,请你在图中落实他的想法;
(2)根据图象以及数据关系,它可能是我们所学习过的 二次 函数图象(选填“一次”、“二次”或“反比例”).请你选择合适的数据求出该函数的表达式;
(3)地铁从开始刹车到下次启动一共用时60秒.求地铁的停靠时间.
(停靠时间指的是地铁刹停后的静止时间)
【点拨】(1)根据描点,连线,画出函数图象即可求解;
(2)观察函数图象即可求解;待定系数法求二次函数解析式即可求解;
(3)将S=0代入,解方程即可求出t的值,再用60﹣t即可得出结论.
【解析】解:(1)描点,连线,如图:
(2)根据图象以及数据关系,它可能是我们所学习过的二次函数,
设S=at2+bt+c,将点(0,256)代入得:c=256,
将(4,196),(8,144)代入S=ax2+bx+256中,
得:,
解得:,
∴该函数的表达式为S=x2﹣16x+256;
故答案为:二次;
(3)依题意,当S=0时,x2﹣16x+256=0,
解得:t1=t2=32,
∴60﹣32=28,
∴地铁的停靠时间为28秒.
【点睛】本题考查了二次函数的应用,熟练掌掌握二次函数性质是解题的关键.
11.(2024 浙江模拟)某个农场有一个花卉大棚,是利用部分墙体建造的.其横截面顶部为抛物线型,大棚的一端固定在墙体OA上,另一端固定在墙体BC上,其横截面有2根支架DE,FG,相关数据如图1所示,其中支架DE=BC,OF=DF=BD,这个大棚用了400根支架.
为增加棚内空间,农场决定将图1中棚顶向上调整,支架总数不变,对应支架的长度变化,如图2所示,调整后C与E上升相同的高度,增加的支架单价为60元/米(接口忽略不计),需要增加的经费不超过32000元.
(1)分别以OB和OA所在的直线为x轴和y轴建立平面直角坐标系.
①求出改造前的函数解析式.
②当CC′=1米,求GG′的长度.
(2)只考虑经费情况下,求出CC′的最大值.
【点拨】(1)①设改造前的函数解析式为y=ax2+bx+c,根据所建立的平面直角坐标系得到A(0,1),E(4,3.4),C(6,3.4),然后代入解析式得到关于a、b、c的方程组,求解即可;
②根据已知条件得到函数的解析式,再利用函数解析式得到C′、E′的坐标即可得到结论;
(2)根据已知条件表示出G′、E′的坐标得到a的不等式,进而得到CC′的最大值.
【解析】解:(1)①如图,以O为原点,分别以OB和OA所在的直线为x轴和y轴建立如图所示的平面直角坐标系,
由题意可知:A(0,1),E(4,3.4),C(6,3.4),
设改造前的抛物线解析式为y=ax2+bx+c,
∴,
解得:,
∴改造前的抛物线的函数表达式为;
②如图,建立与(1)相同的平面直角坐标系,
由①知改造前抛物线的解析式为,
∴对称轴为直线,
设改造后抛物线解析式为:,
∵调整后C与E上升相同的高度,且CC′=1,
∴对称轴为直线x=5,则有,
当x=6时,y=4.4,
∴36c+6d+1=4.4,
∴,,
∴改造后抛物线解析式为:,
当x=2时,
改造前:,
改造后:,
∴(米),
∴GG′的长度为米;
(2)如(2)题图,设改造后抛物线解析式为y=ax2﹣10ax+1,
∵当x=2时,y=a×22﹣10a×2+1=﹣16a+1,
当x=4时,y=a×42﹣10a×4+1=﹣24a+1,
∴G′(2,﹣16a+1),E′(4,﹣24a+1),
∴,
由题意可列不等式:(﹣40a﹣4)×200×60≤32000,
解得:,
∵CC'=EE'=﹣24a+1﹣3.4,
要使最大,需a最小,
∴当时,CC′的值最大,最大值为1.6米.
【点睛】本题考查用待定系数法求二次函数的解析式,二次函数的对称轴,二次函数的实际应用,一元一次不等式的实际应用等知识点.掌握二次函数的性质及是一元一次不等式的应用解题的关键.
12.(2024 镇海区一模)根据以下素材,探索完成任务.
设计跳长绳方案
素材1:某校组织跳长绳比赛,要求如下:(1)每班需要报名跳绳同学9人,摇绳同学2人;(2)跳绳同学需站成一路纵队,原地起跳,如图1.
素材2:某班进行赛前训练,发现:(1)当绳子摇至最高处或最低处时,可近似看作两条对称分布的抛物线,已知摇绳同学之间水平距离为6m,绳子最高点为2m,摇绳同学的出手高度均为1m,如图2;(2)9名跳绳同学身高如右表. 身高(m)1.701.731.751.80人数2241
素材3:观察跳绳同学的姿态(如图3),发现:(1)跳绳时,人的跳起高度在0.25m及以下较为舒适;(2)当长绳摇至最高处时,人正屈膝落地,此时头顶到地面的高度是身高的.
问题解决
任务1:确定长绳形状.请在图2中以长绳触地点为原点建立直角坐标系,并求出长绳摇至最高处时,对应抛物线的解析式.
任务2:确定排列方案.该班班长决定:以长绳的触地点为中心,将同学按“中间高,两边低”的方式对称排列,同时保持0.45m的间距.请计算当绳子在最高点时,长绳是否会触碰到最边侧的同学.
任务3:方案优化改进.据最边侧同学反映:由于跳起高度过高,导致不舒适,希望作出调整.班长给出如下方案:摇绳同学在绳即将触地时,将出手高度降低至0.85m.此时中段长绳将贴地形成一条线段(x线段AB),而剩余的长绳则保持形状不变,如图4.请你通过计算说明,该方案是否可解决同学反映的问题.
【点拨】(1)按照题意建立平面直角坐标系,易得抛物线的对称轴为y轴,于y轴交于点(0,2),并且经过点(﹣3,1),设出相应的函数解析式,进而把点(﹣3,1)代入可得二次项系数的值,即可求得长绳摇至最高处时,对应抛物线的解析式;
(2)9个同学,最高的同学在正中间,那么右边将有4个同学,易得最右侧同学所在的横坐标,代入(1)中得到的解析式,可得最右侧同学所在的地方抛物线的高度,计算出最右侧同学屈膝后的身高,与抛物线的高度比较可判断绳子在最高点时,长绳是否会触碰到最边侧的同学;
(3)根据抛物线的形状相同可得绳子摇至最低处时,抛物线解析式,进而可得平移后新的抛物线解析式,取最右侧同学的横坐标代入可得最右侧同学跳绳的高度,与舒适高度0.25比较即可判断方案能否解决问题.
【解析】解:任务1:如图建立平面直角坐标系.
设长绳摇至最高处时,对应抛物线的解析式为:y=ax2+2(a≠0).
∵经过点(﹣3,1).
∴9a+2=1.
解得:a=﹣.
∴长绳摇至最高处时,对应抛物线的解析式为:y=﹣x2+2.
任务2.最右侧同学所在的横坐标为:0.45×4=1.8.
当x=1.8时,y=﹣×(1.8)2+2=1.64.
∵长绳摇至最高处时,人正屈膝落地,此时头顶到地面的高度是身高的,
∴最右侧同学屈膝后的身高为:1.70×=1.615.
∵1.615<1.64.
∴绳子在最高点时,长绳不会触碰到最边侧的同学.
任务3.当绳子摇至最低处时,抛物线解析式可表示为y=x2.
∵出手高度降低至0.85m.
∴抛物线下降0.15m.
∴下移后的抛物线解析式为:y=x2﹣0.15.
当x=1.8时,y=×1.82﹣0.15=0.21.
∵0.21<0.25,
∴方案能解决同学反映的问题.
【点睛】本题考查二次函数的应用.用到的知识点为:二次函数的形状相同,开口方向不同,则两个函数二次项的系数互为相反数;二次函数上下平移,只改变函数值,上加下减.
13.(2024 上城区校级模拟)
设计喷水方案
素材1 图1为某公园的圆形喷水池,图2是其示意图,O为水池中心,喷头A、B之间的距离为20米,喷射水柱呈抛物线形,水柱距水池中心7m处达到最高,高度为5m,水池中心处有一个圆柱形蓄水池,其底面直径CD为12m,高CF为1.8米
素材2 如图3、图4,拟将在圆柱形蓄水池中心处建一能伸缩高度的喷水装置OP(OP⊥CD),要求水柱不能碰到图2中的水柱,也不能落在蓄水池外面.经调研,目前市场有两种喷水头均能喷射与图2中形状相同的抛物线.其中,甲喷水头以点P为最高点向四周喷射水柱(如图3),乙喷水头喷射水柱的最高点与点P的高度差为0.8m(如图4).
问题解决
任务1 确定水柱形状 在图2中以点O为坐标原点,水平方向为轴建立直角坐标系,求左边这条抛物线的函数表达式.
任务2 选择喷水装置甲,确定喷水装置的最高高度 若选择甲装置(图3),为防止水花溅出,当落水点G、M之间的距离满足时,OP不能再升高,求此时OP的最高高度.
任务3 选择喷水装置乙,拟定喷水装置的高度范围 若选择乙装置(图4),为了美观,要求OP喷出的水柱高度不低于5m,求喷水装置OP高度的变化范围.
【点拨】任务1.易得左侧抛物线的顶点坐标为(﹣7,5)以及点A的坐标(﹣10,0).用顶点式表示出所求的抛物线解析式,把点A的坐标代入即可求得二次函数的二次项系数,即可求得抛物线的解析式;
任务2.设OP长m米,则点P的坐标为(0,m).可设甲喷水头形成的抛物线解析式为:y=﹣x2+m.根据任务1中的抛物线解析式可得点M的坐标,进而可得FM的长度,根据GM=FM,可得GM的长度,即可求得点G的坐标,代入所设的抛物线解析式,即可求得m的值,也就求出了OP的最高高度;
任务3.乙喷水头喷出的抛物线的顶点坐标可设为:(h,m+0.8).用顶点式表示出乙喷水头喷出的抛物线的解析式,把点P的坐标代入可得h的值,进而根据OP喷出的水柱高度不低于5m,取顶点的纵坐标不低于5可得m的一个范围,进而根据水柱不能碰到图2中的水柱,也不能落在蓄水池外面.取点M的坐标代入所求的抛物线解析式可得m的值,即可求得m的取值范围,也就求得了喷水装置OP高度的变化范围.
【解析】解:任务1.如图以点O为坐标原点,水平方向为x轴建立直角坐标系.
∵A、B之间的距离为20米,
∴点A的坐标为(﹣10,0).
∵水柱距水池中心7m处达到最高,高度为5m,
∴左侧抛物线的顶点坐标为(﹣7,5).
∴设左侧抛物线的解析式为:y=a(x+7)2+5.
∴a(﹣10+7)2+5=0.
解得:a=﹣.
∴左边抛物线的函数表达式为:y=﹣(x+7)2+5.
任务2.设OP长m米,则点P的坐标为(0,m).
∵甲喷水头喷射与图2中形状相同的抛物线,并且两个抛物线的开口方向相同.
∴甲喷水头形成的抛物线解析式为:y=﹣x2+m.
由任务1得:左边抛物线的函数表达式为:y=﹣(x+7)2+5.
当y=1.8时,1.8=﹣(x+7)2+5.
解得:x1=﹣9.4(不合题意,舍去),x2=﹣4.6.
∴点M的横坐标为:﹣4.6.
∵CD为12m,
∴OC=6m.
∴FM=6﹣|﹣4.6|=1.4.
∵GM=FM,
∴GM=0.4.
∴点G的横坐标是﹣4.6+0.4=﹣4.2.
∴点G的坐标是(﹣4.2,1.8).
∴1.8=﹣×(﹣4.2)2+m.
解得:m=.
∴OP的最高高度为米.
任务3.如图,建立平面直角坐标系.以y轴左侧的抛物线为例.
设OP长m米,则点P的坐标为(0,m).
∵乙喷水头喷射水柱的最高点与点P的高度差为0.8 m,
∴乙喷水头喷出的抛物线的顶点坐标可设为:(h,m+0.8).
∵乙喷水头喷射与图2中形状相同的抛物线,并且两个抛物线的开口方向相同.
∴乙喷水头形成的抛物线解析式为:y=﹣(x﹣h)2+m+0.8.
把点P的坐标代入得:m=﹣(0﹣h)2+m+0.8.
解得:h=﹣1.2或h=1.2(不合题意,舍去).
∴乙喷水头形成的抛物线解析式为:y=﹣(x+1.2)2+m+0.8.
∵OP喷出的水柱高度不低于5m,
∴最高点(h,m+0.8)的纵坐标不低于5m.
∴m+0.8≥5.
解得:m≥.
∵水柱不能碰到图2中的水柱,也不能落在蓄水池外面.
∴取点M的坐标(﹣4.6,1.8)代入y=﹣(x+1.2)2+m+0.8.
1.8=﹣(﹣4.6+1.2)2+m+0.8.
解得:m=.
∴m<.
∴≤m<.
∴喷水装置OP高度的变化范围为:≤OP<.
【点睛】本题考查二次函数的应用.用到的知识点为:二次函数的形状相同,且开口方向相同,则二次函数的二次项的系数相同.
14.(2024 西湖区一模)在平面直角坐标系中,点(1,m)和(3,n)都在二次函数y=ax2+bx(a≠0,a,b是常数)的图象上.
(1)若m=n=﹣6,求该二次函数的表达式和函数图象的对称轴.
(2)若a=﹣1,m<n,求b的取值范围.
(3)已知点(﹣1,y1),(2,y2),(4,y3)也都在该二次函数图象上,若mn<0且a<0,试比较y1,y2,y3的大小,并说明理由.
【点拨】(1)当m=n=﹣6时,用待定系数法可得二次函数的表达式为y=2x2﹣8x;即可得函数图象的对称轴为直线x=2;
(2)当a=﹣1时,可得,又m<n,故﹣1+b<﹣9+3b,得b>4;
(3)由mn<0,可得(a+b)(9a+3b)<0,又a<0,即可知a+b>0且3a+b<0;求出y1=a﹣b,y2=4a+2b,y3=16a+4b,用作差的方法可得到答案.
【解析】解:(1)当m=n=﹣6时,把(1,﹣6)和(3,﹣6)代入y=ax2+bx得:
,
解得,
∴二次函数的表达式为y=2x2﹣8x;
∵y=2x2﹣8x=2(x﹣2)2﹣8,
∴函数图象的对称轴为直线x=2;
(2)当a=﹣1时,y=﹣x2+bx,
把(1,m)和(3,n)代入得:
,
∵m<n,
∴﹣1+b<﹣9+3b,
解得b>4,
∴b的取值范围是b>4;
(3)把(1,m)和(3,n)代入y=ax2+bx得:
,
∵mn<0,
∴(a+b)(9a+3b)<0,
∴或,
∵a<0,
∴,即无解;
∴a+b>0且3a+b<0;
把(﹣1,y1),(2,y2),(4,y3)代入y=ax2+bx得:
y1=a﹣b,y2=4a+2b,y3=16a+4b,
∴y1﹣y2=a﹣b﹣(4a+2b)=﹣3(a+b)<0,y1﹣y3=a﹣b﹣(16a+4b)=﹣5(3a+b)>0,
∴y1<y2,y1>y3,
∴y3<y1<y2.
【点睛】本题考查二次函数的综合应用,涉及待定系数法,二次函数图象上点坐标的特征,作差法比较大小等,解题的关键是掌握二次函数图象上点坐标的特征和不等式的基本性质.
15.如图,二次函数y=ax2+bx+3(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,C为顶点.
(1)请求出二次函数的表达式及图象的顶点C的坐标.
(2)若点E为抛物线对称轴左侧一点,过点E作x轴平行线交对称轴于点D,若ED=m,试用m的代数式表示CD.
(3)连结EC,过点C作CF⊥EC交抛物线于点F,过点F作x轴的平行线交对称轴于点G,证明:GF DE=1.
【点拨】(1)用待定系数法求函数的解析式即可;
(2)设D(1,t),可得E(1﹣m,t),又由t=﹣(1﹣m)2+2(1﹣m)+3,能求CD=4﹣t=m2;
(3)证明△CDE∽△FGC,可得=,推导出FG=mCG,设F(n,﹣n2+2n+3),则G(1,﹣n2+2n+3),则CG=(n﹣1)2,所以n﹣1=,再由FG=mCG,可求GF DE=mFG=m2 (n﹣1)2=1.
【解析】(1)解:将点A(﹣1,0),B(3,0)代入y=ax2+bx+3,
∴,
解得,
∴抛物线的解析式为y=﹣x2+2x+3;
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点C(1,4);
(2)解:设D(1,t),
∵ED=m,
∴E(1﹣m,t),
∴t=﹣(1﹣m)2+2(1﹣m)+3,
∴CD=4﹣t=m2;
(3)证明:∵ED⊥CD,GF⊥CD,
∴∠EDC=∠CGF=90°,
∵EC⊥CF,
∴∠ECF=90°,
∵∠ECD+∠FCG=90°,∠ECD+∠CED=90°,
∴∠FCG=∠CED,
∴△CDE∽△FGC,
∴=,
∴GF DE=GC CD,
∵ED=m,CD=m2,
∴FG=mCG,
设F(n,﹣n2+2n+3),则G(1,﹣n2+2n+3),
∴CG=4﹣(﹣n2+2n+3)=(n﹣1)2,
∴n﹣1=m(n﹣1)2,
∴n﹣1=,
∵FG=mCG,
∴GF DE=mFG=m2 (n﹣1)2=1.
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,三角形相似的判定及性质是解题的关键.
16.已知二次函数的图象经过原点O和点A(8+t,0),其中t≥0.
(1)当t=0时.
①求y关于x的函数表达式,并求出当x为何值时,y有最大值,最大值为多少?
②当x=m和x=n时(m≠n),函数值相等,求m,n之间的关系式.
(2)当t>0时,在0≤x≤8范围内,y是否存在最大值18?若存在,求出相应的t和x的值,若不存在,请说明理由.
【点拨】(1)①把O(0,0),A(8,0)代入y=﹣x2+bx+c得,可求出y关于x的函数表达式为y=﹣x2+2x;而y=﹣x2+2x=﹣(x﹣4)2+4,故当x为4时,y有最大值,最大值为4;
②根据当x=m和x=n时(m≠n),函数值相等,可得﹣(m﹣4)2+4=﹣(n﹣4)2+4,即可求出m+n=8;
(2)把二次函数的图象经过原点O和点A(8+t,0),,可求出y=﹣x2+x=﹣(x﹣)2+,故抛物线y=﹣x2+x的对称轴为直线x=;①当≥8,即t≥8时,﹣×82+×8=18,解得t的值即可知当t的值为9,x的值为8时,y取得最大值18;②当<8,即0<t<8时,有=18,可解得:t=﹣12﹣8(小于0,舍去)或t=12﹣8(大于8,舍去).
【解析】解:(1)当t=0时,A(8,0),
①把O(0,0),A(8,0)代入y=﹣x2+bx+c得:
,
解得:,
∴y关于x的函数表达式为y=﹣x2+2x;
∵y=﹣x2+2x=﹣(x﹣4)2+4,
∴当x为4时,y有最大值,最大值为4;
②∵当x=m和x=n时(m≠n),函数值相等,
∴﹣(m﹣4)2+4=﹣(n﹣4)2+4,
∴(m﹣n)(m+n﹣8)=0,
∵m﹣n≠0,
∴m+n=8;
(2)在0≤x≤8范围内,y存在最大值18,理由如下:
∵二次函数的图象经过原点O和点A(8+t,0),
∴,
解得,
∴y=﹣x2+x=﹣(x﹣)2+,
∴抛物线y=﹣x2+x的对称轴为直线x=;
①当≥8,即t≥8时,
x=8,y=﹣x2+x取得最大值,
∴﹣×82+×8=18,
解得:t=9,
∴当t的值为9,x的值为8时,y取得最大值18;
②当<8,即0<t<8时,
y=﹣x2+x在顶点处取最大值,
∴=18,
解得:t=﹣12﹣8(小于0,舍去)或t=12﹣8(大于8,舍去),
综上所述,当t的值为9,x的值为8时,y取得最大值18.
【点睛】本题考查二次函数综合应用,涉及待定系数法,二次函数图象上点坐标的特征等知识,解题的关键是分类讨论思想的应用.
09 押浙江卷第23题
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
