第二十一章 一元二次方程单元复习卷(含答案)
文档属性
| 名称 | 第二十一章 一元二次方程单元复习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 249.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 11:09:16 | ||
图片预览

文档简介
九年级数学上册《第二十一章一元二次方程》单元复习卷及解答
选择题
1.下列关于的方程是一元二次方程的是( )
A. B. C. D.
2.若是关于的方程的一个根,则的值为( )
A.1 B.2 C. D.
3.方程的解是( )
A. B. C., D.,
4.下列一元二次方程有两个相等的实数根的是( )
A.x2﹣2x﹣1=0 B.x2+2x+1=0 C.x2﹣x﹣1=0 D.x2﹣x+1=0
5.用配方法解一元二次方程,配方正确的是( )
A. B. C. D.
已知关于x的一元二次方程有两个不相等的实数根,
则实数k的取值范围是( )
A. B.
C.且 D.且
一块矩形菜地的面积是120平方米,如果它的长减少2米,菜地就变成正方形,
则原菜地的长是( )
A.10 B.12 C.13 D.14
已知4是关于x的方程的一个实数根,
并且这个方程的两个实数根恰好是等腰△ABC的两条边的边长,则△ABC的周长为( )
A.7 B.7或 C.或 D.
某商店今年2月份的销售额是8万元,4月份的销售额是18万元,从2月份到4月份,
该店销售额平均每月的增长率是( )
A.12.5% B.25% C.50% D.62.5%
已知一元二次方程 的两个根分别为 和 ,且 ,
则 的值为( )
A. B. C. D.
填空题
11.若是关于的方程的一个根,则的值为_____
12.一元二次方程的根是________________________.
13.若是关于的一元二次方程,则的值是 .
14.一个三角形的两边长分别为3和5,第三边长是方程x2-6x+8=0的根,则三角形的周长为 .
15.若关于x的方程ax2+2(a+2)x+a=0有实数解,那么实数a的取值范围是 .
16.已知一元二次方程x2-4x-3=0的两根为m,n,则-mn+= .
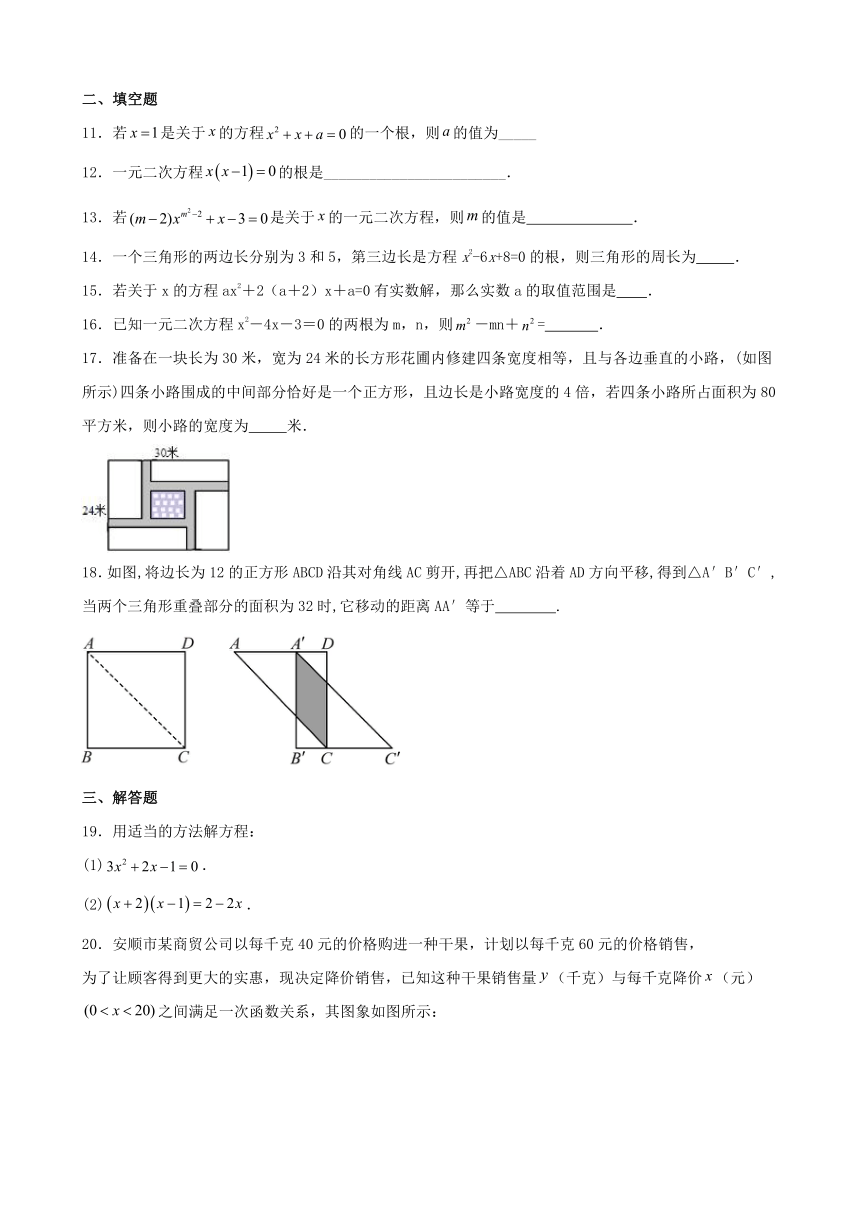
17.准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路,(如图所示)四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为 米.
18.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 .
三、解答题
19.用适当的方法解方程:
(1).
(2).
安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,
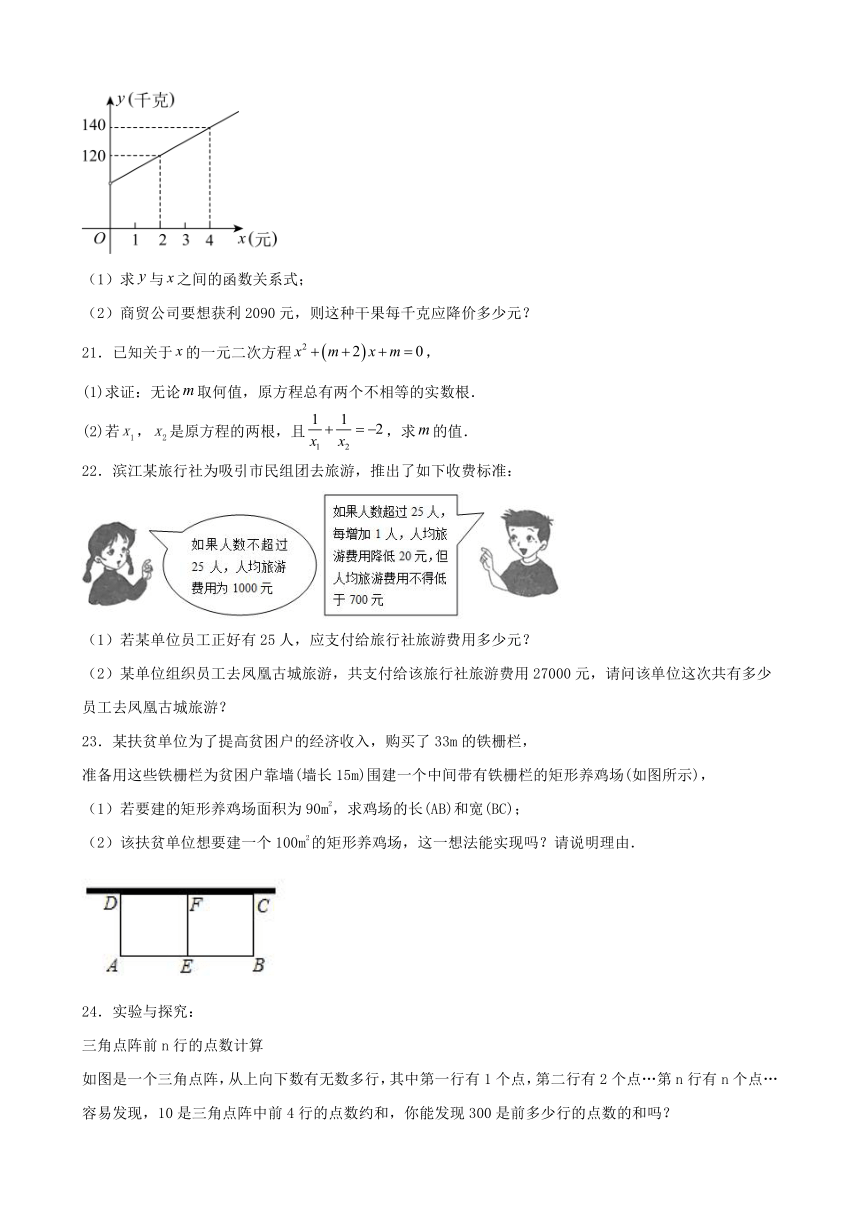
为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量(千克)与每千克降价(元)之间满足一次函数关系,其图象如图所示:
(1)求与之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
21.已知关于的一元二次方程,
(1)求证:无论取何值,原方程总有两个不相等的实数根.
(2)若,是原方程的两根,且,求的值.
22.滨江某旅行社为吸引市民组团去旅游,推出了如下收费标准:
(1)若某单位员工正好有25人,应支付给旅行社旅游费用多少元?
(2)某单位组织员工去凤凰古城旅游,共支付给该旅行社旅游费用27000元,请问该单位这次共有多少员工去凤凰古城旅游?
某扶贫单位为了提高贫困户的经济收入,购买了33m的铁栅栏,
准备用这些铁栅栏为贫困户靠墙(墙长15m)围建一个中间带有铁栅栏的矩形养鸡场(如图所示),
(1)若要建的矩形养鸡场面积为90m2,求鸡场的长(AB)和宽(BC);
(2)该扶贫单位想要建一个100m2的矩形养鸡场,这一想法能实现吗?请说明理由.
24.实验与探究:
三角点阵前n行的点数计算
如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点…
容易发现,10是三角点阵中前4行的点数约和,你能发现300是前多少行的点数的和吗?
如果要用试验的方法,由上而下地逐行的相加其点数,虽然你能发现1+2+3+4+…+23+24=300.得知300是前24行的点数的和,但是这样寻找答案需我们先探求三角点阵中前n行的点数的和与n的数量关系
前n行的点数的和是1+2+3+…+(n﹣2)+(n﹣1)+n,可以发现.
2×[1+2+3+…+(n﹣2)+(n﹣1)+n]
=[1+2+3+…+(n﹣2)+(n﹣1)+n]+[n+(n﹣1)+(n﹣2)+…3+2+1]
把两个中括号中的第一项相加,第二项相加…第n项相加,上式等号的后边变形为这n个小括号都等于n+1,整个式子等于n(n+1),于是得到
1+2+3+…+(n﹣2)+(n﹣1)+n=n(n+1)
这就是说,三角点阵中前n项的点数的和是n(n+1)
下列用一元二次方程解决上述问题
设三角点阵中前n行的点数的和为300,则有n(n+1)
整理这个方程,得:n2+n﹣600=0
解方程得:n1=24,n2=25
根据问题中未知数的意义确定n=24,即三角点阵中前24行的点数的和是300.
请你根据上述材料回答下列问题:
(1)三角点阵中前n行的点数的和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
(2)如果把图中的三角点阵中各行的点数依次换成2、4、6、…、2n、…,你能探究处前n行的点数的和满足什么规律吗?这个三角点阵中前n行的点数的和能使600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
九年级数学上册《第二十一章一元二次方程》单元复习卷
参考解答
选择题
1.C 2.D 3.C 4.B. 5.A. 6 .C. 7 .B 8 .C. 9 .C. 10 .A.
填空题
11.【答案】-2 12.【答案】 13.【答案】﹣2 14.【答案】12
15.【答案】a≥-1.16.【答案】25 17.【答案】1.25 18.【答案】4或8
三、解答题
19.(1)解:,
,
则或,
解得,,
所以,原方程的解为,;
(2)解:
,
则,
或,
解得,.
所以,原方程的解为,.
20.解:(1)设一次函数解析式为:,根据图象可知:当,;当,;
∴,解得:,
∴与之间的函数关系式为;
(2)由题意得:,
整理得:,解得:.,
∵让顾客得到更大的实惠,∴.
答:商贸公司要想获利2090元,这种干果每千克应降价9元.
21.(1)证明:∵,
∴无论取何值,原方程总有两个不相等的实数根;
(2)解:由题可知,,,
∴,
解得,
经检验m=2有意义.
22.解:(1)1000×25=25000(元).
答:应支付给旅行社旅游费用25000元.
(2)设该单位这次共有x名员工去凤凰古城旅游,
27000÷1000=27>25,27000÷700=不为整数,
25+=40,
,
依题意,得:[1000﹣20(x﹣25)]x=27000,
整理,得:x2﹣75x+1350=0,
解得:x1=30,x2=45(不合题意,舍去).
答:该单位这次共有30名员工去凤凰古城旅游.
23.解:(1)设BC=xm,则AB=(33-3x)m,
依题意,得:x(33-3x)=90,
解得:x1=6,x2=5.
当x=6时,33-3x=15,符合题意,
当x=5时,33-3x=18,18>15,不合题意,舍去.
答:鸡场的长(AB)为15m,宽(BC)为6m.
(2)不能,理由如下:
设BC=ym,则AB=(33-3y)m,
依题意,得:y(33-3y)=100,
整理,得:3y2-33y+100=0.
∵△=(-33)2-4×3×100=-111<0,
∴该方程无解,即该扶贫单位不能建成一个100m2的矩形养鸡场.
24.解:(1)由题意可得:n(n+1)=600,
整理得n2+n﹣1200=0,
此方程无正整数解,
∴三角点阵中前n行的点数的和不可能是600.
(2)由题意可得:2+4+6+…+2n=2(1+2+3+…+n)=2×n(n+1)= n(n+1),
依题意,得n(n+1)=600,
整理得n2+n﹣600=0,(n+25)(n﹣24)=0,
∴n1=﹣25,n2=24.
∵n为正整数,∴n=24.
∴n的值是24.
选择题
1.下列关于的方程是一元二次方程的是( )
A. B. C. D.
2.若是关于的方程的一个根,则的值为( )
A.1 B.2 C. D.
3.方程的解是( )
A. B. C., D.,
4.下列一元二次方程有两个相等的实数根的是( )
A.x2﹣2x﹣1=0 B.x2+2x+1=0 C.x2﹣x﹣1=0 D.x2﹣x+1=0
5.用配方法解一元二次方程,配方正确的是( )
A. B. C. D.
已知关于x的一元二次方程有两个不相等的实数根,
则实数k的取值范围是( )
A. B.
C.且 D.且
一块矩形菜地的面积是120平方米,如果它的长减少2米,菜地就变成正方形,
则原菜地的长是( )
A.10 B.12 C.13 D.14
已知4是关于x的方程的一个实数根,
并且这个方程的两个实数根恰好是等腰△ABC的两条边的边长,则△ABC的周长为( )
A.7 B.7或 C.或 D.
某商店今年2月份的销售额是8万元,4月份的销售额是18万元,从2月份到4月份,
该店销售额平均每月的增长率是( )
A.12.5% B.25% C.50% D.62.5%
已知一元二次方程 的两个根分别为 和 ,且 ,
则 的值为( )
A. B. C. D.
填空题
11.若是关于的方程的一个根,则的值为_____
12.一元二次方程的根是________________________.
13.若是关于的一元二次方程,则的值是 .
14.一个三角形的两边长分别为3和5,第三边长是方程x2-6x+8=0的根,则三角形的周长为 .
15.若关于x的方程ax2+2(a+2)x+a=0有实数解,那么实数a的取值范围是 .
16.已知一元二次方程x2-4x-3=0的两根为m,n,则-mn+= .
17.准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路,(如图所示)四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为 米.
18.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 .
三、解答题
19.用适当的方法解方程:
(1).
(2).
安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,
为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量(千克)与每千克降价(元)之间满足一次函数关系,其图象如图所示:
(1)求与之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
21.已知关于的一元二次方程,
(1)求证:无论取何值,原方程总有两个不相等的实数根.
(2)若,是原方程的两根,且,求的值.
22.滨江某旅行社为吸引市民组团去旅游,推出了如下收费标准:
(1)若某单位员工正好有25人,应支付给旅行社旅游费用多少元?
(2)某单位组织员工去凤凰古城旅游,共支付给该旅行社旅游费用27000元,请问该单位这次共有多少员工去凤凰古城旅游?
某扶贫单位为了提高贫困户的经济收入,购买了33m的铁栅栏,
准备用这些铁栅栏为贫困户靠墙(墙长15m)围建一个中间带有铁栅栏的矩形养鸡场(如图所示),
(1)若要建的矩形养鸡场面积为90m2,求鸡场的长(AB)和宽(BC);
(2)该扶贫单位想要建一个100m2的矩形养鸡场,这一想法能实现吗?请说明理由.
24.实验与探究:
三角点阵前n行的点数计算
如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点…
容易发现,10是三角点阵中前4行的点数约和,你能发现300是前多少行的点数的和吗?
如果要用试验的方法,由上而下地逐行的相加其点数,虽然你能发现1+2+3+4+…+23+24=300.得知300是前24行的点数的和,但是这样寻找答案需我们先探求三角点阵中前n行的点数的和与n的数量关系
前n行的点数的和是1+2+3+…+(n﹣2)+(n﹣1)+n,可以发现.
2×[1+2+3+…+(n﹣2)+(n﹣1)+n]
=[1+2+3+…+(n﹣2)+(n﹣1)+n]+[n+(n﹣1)+(n﹣2)+…3+2+1]
把两个中括号中的第一项相加,第二项相加…第n项相加,上式等号的后边变形为这n个小括号都等于n+1,整个式子等于n(n+1),于是得到
1+2+3+…+(n﹣2)+(n﹣1)+n=n(n+1)
这就是说,三角点阵中前n项的点数的和是n(n+1)
下列用一元二次方程解决上述问题
设三角点阵中前n行的点数的和为300,则有n(n+1)
整理这个方程,得:n2+n﹣600=0
解方程得:n1=24,n2=25
根据问题中未知数的意义确定n=24,即三角点阵中前24行的点数的和是300.
请你根据上述材料回答下列问题:
(1)三角点阵中前n行的点数的和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
(2)如果把图中的三角点阵中各行的点数依次换成2、4、6、…、2n、…,你能探究处前n行的点数的和满足什么规律吗?这个三角点阵中前n行的点数的和能使600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
九年级数学上册《第二十一章一元二次方程》单元复习卷
参考解答
选择题
1.C 2.D 3.C 4.B. 5.A. 6 .C. 7 .B 8 .C. 9 .C. 10 .A.
填空题
11.【答案】-2 12.【答案】 13.【答案】﹣2 14.【答案】12
15.【答案】a≥-1.16.【答案】25 17.【答案】1.25 18.【答案】4或8
三、解答题
19.(1)解:,
,
则或,
解得,,
所以,原方程的解为,;
(2)解:
,
则,
或,
解得,.
所以,原方程的解为,.
20.解:(1)设一次函数解析式为:,根据图象可知:当,;当,;
∴,解得:,
∴与之间的函数关系式为;
(2)由题意得:,
整理得:,解得:.,
∵让顾客得到更大的实惠,∴.
答:商贸公司要想获利2090元,这种干果每千克应降价9元.
21.(1)证明:∵,
∴无论取何值,原方程总有两个不相等的实数根;
(2)解:由题可知,,,
∴,
解得,
经检验m=2有意义.
22.解:(1)1000×25=25000(元).
答:应支付给旅行社旅游费用25000元.
(2)设该单位这次共有x名员工去凤凰古城旅游,
27000÷1000=27>25,27000÷700=不为整数,
25+=40,
,
依题意,得:[1000﹣20(x﹣25)]x=27000,
整理,得:x2﹣75x+1350=0,
解得:x1=30,x2=45(不合题意,舍去).
答:该单位这次共有30名员工去凤凰古城旅游.
23.解:(1)设BC=xm,则AB=(33-3x)m,
依题意,得:x(33-3x)=90,
解得:x1=6,x2=5.
当x=6时,33-3x=15,符合题意,
当x=5时,33-3x=18,18>15,不合题意,舍去.
答:鸡场的长(AB)为15m,宽(BC)为6m.
(2)不能,理由如下:
设BC=ym,则AB=(33-3y)m,
依题意,得:y(33-3y)=100,
整理,得:3y2-33y+100=0.
∵△=(-33)2-4×3×100=-111<0,
∴该方程无解,即该扶贫单位不能建成一个100m2的矩形养鸡场.
24.解:(1)由题意可得:n(n+1)=600,
整理得n2+n﹣1200=0,
此方程无正整数解,
∴三角点阵中前n行的点数的和不可能是600.
(2)由题意可得:2+4+6+…+2n=2(1+2+3+…+n)=2×n(n+1)= n(n+1),
依题意,得n(n+1)=600,
整理得n2+n﹣600=0,(n+25)(n﹣24)=0,
∴n1=﹣25,n2=24.
∵n为正整数,∴n=24.
∴n的值是24.
同课章节目录
