五年级数学上册 最新人教版第四单元 第3课时 可能性的大小(2)(课件)(共29张PPT)
文档属性
| 名称 | 五年级数学上册 最新人教版第四单元 第3课时 可能性的大小(2)(课件)(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 13:42:16 | ||
图片预览



文档简介
(共29张PPT)
可能性
人教版五年级数学上册
第3课时 根据随机现象结果进行推测
一、复习旧知,激励导入
(1)小明要从盒子中摸出一个球,你觉得他会摸出什么颜色的球?
(2)他摸出什么颜色的球的可能性大?为什么?
摸出红球的可能性大,因为口袋中红球的数量比黄球多。
二、试验猜想,探究新知
猜一猜:摸到哪种颜色的球的可能性大?
里面有
两种颜色的小球
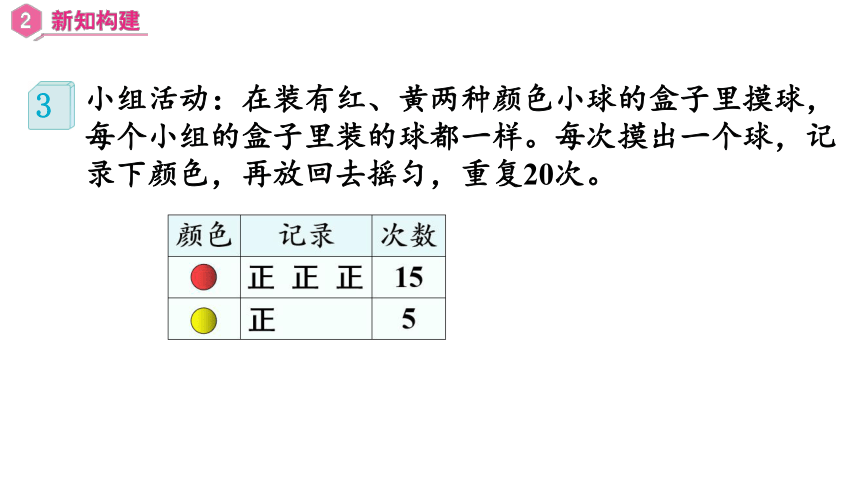
小组活动:在装有红、黄两种颜色小球的盒子里摸球,每个小组的盒子里装的球都一样。每次摸出一个球,记录下颜色,再放回去摇匀,重复20次。
3
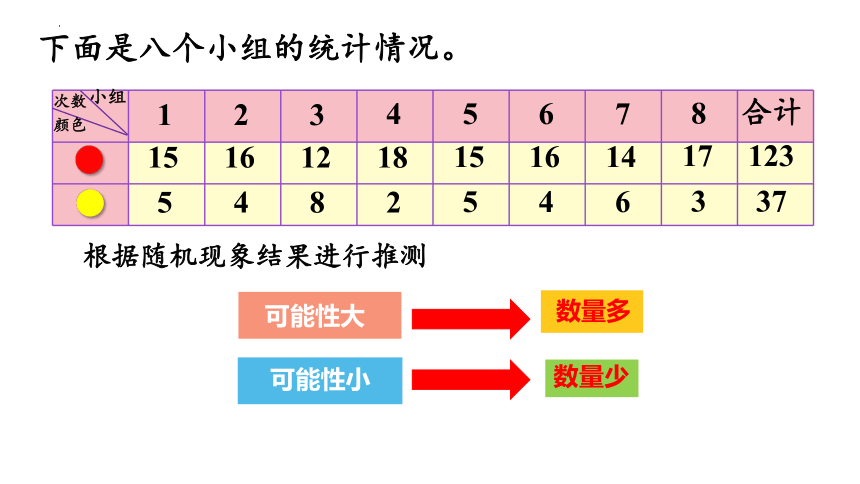
下面是八个小组的统计情况。
次数
颜色
小组
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
(1)每次都摸出了哪些颜色的球?
(2)各个小组的试验结果一样吗?有什么共同点?
(3)为什么每个小组都是摸出红球的次数多,摸出黄球的次数少?盒子里的红球和黄球数量相等吗?
下面是八个小组的统计情况。
次数
颜色
小组
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
次数多
被摸出的可能性大
数量多
次数少
被摸出的可能性小
数量少
的数量多, 的数量少。
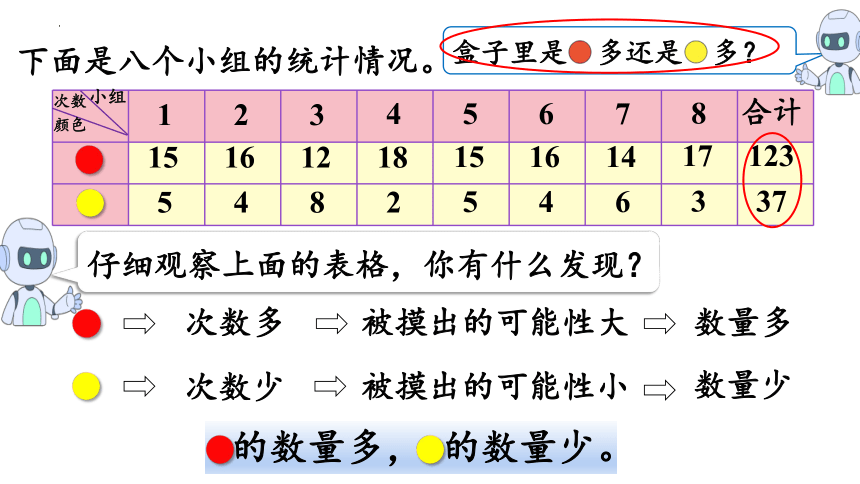
仔细观察上面的表格,你有什么发现?
盒子里是 多还是 多?
次数
颜色
小组
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
下面是八个小组的统计情况。
哇,盒子里果然是 多。
真的是这样吗?让我们来验证一下吧。
下面是八个小组的统计情况。
次数
颜色
小组
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
根据随机现象结果进行推测
可能性大
数量多
可能性小
数量少
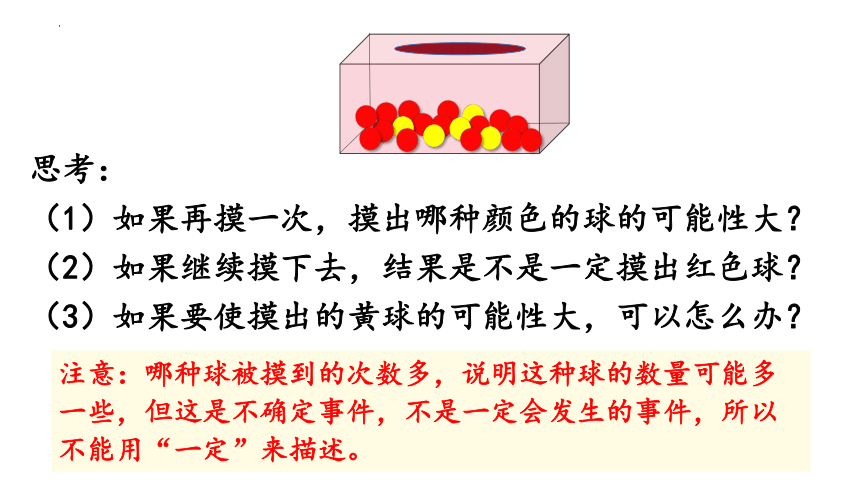
思考:
(1)如果再摸一次,摸出哪种颜色的球的可能性大?
(2)如果继续摸下去,结果是不是一定摸出红色球?
(3)如果要使摸出的黄球的可能性大,可以怎么办?
注意:哪种球被摸到的次数多,说明这种球的数量可能多一些,但这是不确定事件,不是一定会发生的事件,所以不能用“一定”来描述。
思考:根据前面的探究,你认为可能性的大小与什么有关系?
1.可能性的大小与数量有关,在总数中所占的数量越多,可能性就越大。
2.记录的次数越多,说明被摸到的可能性越大,对应的物体数量就可能相对多些。
归纳总结:
事件发生的可能性的大小能反映出个体数量的多少。
可能性大,对应的个体数量可能就多一些;
可能性小,对应的个体数量可能就少一些;
可能性相等,对应的个体数量一样多。
事件发生可能性大小的应用:
1.从右面的盒子里摸出一个棋子,可能是什么颜色?猜一猜:摸出哪种颜色棋子的可能性最大?,摸出哪种颜色棋子的可能性最小?
做一做
答:摸出一个棋子,可能是红色、蓝色或黄色;
盒子里红色棋子最多,所以摸出红色棋子的可能性最大;
盒子里黄色棋子最少,所以摸出黄色棋子的可能性最小。
(教材P46 做一做T1)
2.
全班每人掷一次。
朝上的有_____人。
朝上的有_____人。
朝上的可能性大还是 朝上的可能性大?
两面朝上的可能性应该是相等的。可为什么出现一个多一个少的现象呢?
如果有更多的人来掷,结果会怎样呢?
(教材第46页“做一做”)
虽然可能性相等,但出现正、反面的次数不一定相等。
哪面朝上?
做一做
14
1、每小组每人抛硬币1次,抛硬币时用力均匀,高度适中;
2、以小组为单位分别统计相关数据,填入实验报告单 。
3、小组成员分工协作,看哪个小组合作最好,完成得最快!
实验要求:
全班每人掷一次。
朝上的有_____人。
朝上的有_____人。
哪面朝上?
4.思考:正面朝上的次数与总次数有什么样的关系?
做一做
2.
15
五年级1班同学做抛硬币体验的数据
试验小组 抛硬币次数 正面朝上次数 反面朝上次数
第一小组 12 5 7
第二小组 12 6 6
第三小组 12 7 5
第四小组 14 8 6
总计 50 26 24
朝上的可能性大还是 朝上的可能性大?
出现正面和出现反面的可能性是相同的,都是 。
1
2
“可能性”的大小可用分数来表示。
两面朝上的可能性应该是相等的。可为什么出现一个多一个少的现象呢?
虽然可能性相等,但出现正、反面朝上的次数不一定相等。
试验者 抛硬币总次数 正面朝上次数 反面朝上次数
德 摩根 4040 2048 1992
蒲丰 4092 2048 2044
费勒 10000 4979 5021
皮尔逊 12000 6019 5981
皮尔逊 24000 12012 11988
以下是四位数学家做抛币实验的结果
如果抛硬币的次数越多,结果会怎样呢?
抛硬币的次数越多,出现正、反面的朝上的次数越接近。
1.按要求涂一涂。
摸出的一定是 。
摸出的不可能是 。
摸出的可能是 。
必须全部涂蓝色。
答案不唯一,
只要不涂黄色即可。
答案不唯一,
至少有一个涂橘色,
但不能都涂橘色。
(教材第47页第4题)
2.
全班猜一猜。
盒子
人数
1号
2号
3号
4号
只有一枚硬币,可能在哪个盒子里?
猜对的人多,还是猜错的人多?
猜错的可能有3种,猜对的可能有1种,3>1,猜错的可能性大。
(教材第48页第9题)
(教材第49页第10题)
5红面1蓝面, 4红面2蓝面。
4. 给 涂上红、蓝两种颜色,要使掷出红色朝上的可能性比蓝色大,应该怎么涂?
红色的面应比蓝色的面多。
或5红1蓝。
所以可以涂 4红2蓝
共6个面
5.把10张卡片放入纸袋,随意摸一张,要使摸出数字
“1”的可能性最大,数字“5”的可能性最小,卡片上可以是什么数字?请你填一填。
1
1
1
1
1
1
1
1
5
卡片中 “1”的张数要最多;
卡片中 “5”的张数要最少。
(教材第49页第11题)
1
1
1
1
1
1
1
1
1
5
5
1
1
1
1
1
1
1
2
2
5
1
1
1
1
1
1
4
4
4
5
10张卡片中可以只有“1”和“5”两个数字,也可以有其他数字。
5.把10张卡片放入纸袋,随意摸一张,要使摸出数字
“1”的可能性最大,数字“5”的可能性最小,卡片上可以是什么数字?请你填一填。
6.每个盒子中都放着大小相同、颜色不同的10个球,
该怎么放?
(1)任意摸出1个球,摸出红球的可能性大。
(2)任意摸出1个球,一定是红球。
( )个红球
( )个黄球
( )个红球
( )个黄球
1
2
9
1
8
2
7
3
6
4
10
0
(3)任意摸出1个球,摸出红球和黄球的可能性一样大。
(4)任意摸出1个球,不可能是红球。
( )个红球
( )个黄球
( )个红球
( )个黄球
3
4
0
10
5
5
(1)
(2)
7. 小宇要设计一个转盘,上面画着 和 两种图案。如果要达到下面的要求,他该怎么画?
(1)任意转动1次,转到 的可能性大。
(2)任意转动1次,一定转到 。
的数量要多
都是
(答案不唯一)
(3)
(4)
(3)任意转动1次,转到 和 的可能性一样大。
(4)任意转到1次,不可能转到 。
和 的数量一样多
只有 ,没有
7. 小宇设计了一个转盘,上面画有 和 两种图案。宁宁转了20次,结果如右表。
8次 12次
根据表中的数据,小宇设计
的转盘最有可能是 ;不
可能是 。
(1)
(2)
(3)
(1)
(3)
8. 小亮和小强玩摸球游戏(盒子里的球如右图所示)。一次摸 2个球,摸后放回,如果摸到2个红球算小亮赢,摸到1红1蓝,算小强赢,摸到2蓝不分输赢,重摸。他们俩谁获胜的可能性大?
小亮赢的情形只有一种,而小强赢的情形有四种,很明显,小强获胜的可能性大。
1
1
2
1
1
2
1
2
小亮赢:
小强赢:
2
1
2
2
不分输赢:
先给盒子中的球做上标记,比如可以标记为 和 ,再列出他们俩赢的情形。
1
2
1
2
可能性的大小
可能性大小
数量越多
可能性越大
与数量有关
数量越少
可能性越小
概率问题
概率主要研究不确定现象,它起源于博奕问题。15~16世纪,意大利数学家们曾讨论过“如果两人赌博提前结束,该如何分配赌金”等问题。比如,两个人做掷硬币游戏。掷出正面甲得1分,掷出反面乙得1分,先得到10分的人赢得蛋糕,如果游戏因故中途结束,此时甲得了8分,乙得了7分,那么他们该如何分配这个蛋糕呢?
为了回答上述问题,人们对不确定现象进行了大量的研究,前面已列举了历史上一些数学家所做的掷硬币试验的数据。
对不确定现象的研究,最终导致了概率论与数理统计这门学科的出现。它自产生之日起,就与人们的实际生活有着紧密的联系,并且解决了许多科技发展中的问题。正因为如此,这门学科有着很强的生命力和广阔的发展前景。
可能性
人教版五年级数学上册
第3课时 根据随机现象结果进行推测
一、复习旧知,激励导入
(1)小明要从盒子中摸出一个球,你觉得他会摸出什么颜色的球?
(2)他摸出什么颜色的球的可能性大?为什么?
摸出红球的可能性大,因为口袋中红球的数量比黄球多。
二、试验猜想,探究新知
猜一猜:摸到哪种颜色的球的可能性大?
里面有
两种颜色的小球
小组活动:在装有红、黄两种颜色小球的盒子里摸球,每个小组的盒子里装的球都一样。每次摸出一个球,记录下颜色,再放回去摇匀,重复20次。
3
下面是八个小组的统计情况。
次数
颜色
小组
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
(1)每次都摸出了哪些颜色的球?
(2)各个小组的试验结果一样吗?有什么共同点?
(3)为什么每个小组都是摸出红球的次数多,摸出黄球的次数少?盒子里的红球和黄球数量相等吗?
下面是八个小组的统计情况。
次数
颜色
小组
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
次数多
被摸出的可能性大
数量多
次数少
被摸出的可能性小
数量少
的数量多, 的数量少。
仔细观察上面的表格,你有什么发现?
盒子里是 多还是 多?
次数
颜色
小组
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
下面是八个小组的统计情况。
哇,盒子里果然是 多。
真的是这样吗?让我们来验证一下吧。
下面是八个小组的统计情况。
次数
颜色
小组
15
5
16
4
12
8
18
2
15
5
16
4
14
6
17
3
123
37
1
2
3
4
5
6
7
8
合计
根据随机现象结果进行推测
可能性大
数量多
可能性小
数量少
思考:
(1)如果再摸一次,摸出哪种颜色的球的可能性大?
(2)如果继续摸下去,结果是不是一定摸出红色球?
(3)如果要使摸出的黄球的可能性大,可以怎么办?
注意:哪种球被摸到的次数多,说明这种球的数量可能多一些,但这是不确定事件,不是一定会发生的事件,所以不能用“一定”来描述。
思考:根据前面的探究,你认为可能性的大小与什么有关系?
1.可能性的大小与数量有关,在总数中所占的数量越多,可能性就越大。
2.记录的次数越多,说明被摸到的可能性越大,对应的物体数量就可能相对多些。
归纳总结:
事件发生的可能性的大小能反映出个体数量的多少。
可能性大,对应的个体数量可能就多一些;
可能性小,对应的个体数量可能就少一些;
可能性相等,对应的个体数量一样多。
事件发生可能性大小的应用:
1.从右面的盒子里摸出一个棋子,可能是什么颜色?猜一猜:摸出哪种颜色棋子的可能性最大?,摸出哪种颜色棋子的可能性最小?
做一做
答:摸出一个棋子,可能是红色、蓝色或黄色;
盒子里红色棋子最多,所以摸出红色棋子的可能性最大;
盒子里黄色棋子最少,所以摸出黄色棋子的可能性最小。
(教材P46 做一做T1)
2.
全班每人掷一次。
朝上的有_____人。
朝上的有_____人。
朝上的可能性大还是 朝上的可能性大?
两面朝上的可能性应该是相等的。可为什么出现一个多一个少的现象呢?
如果有更多的人来掷,结果会怎样呢?
(教材第46页“做一做”)
虽然可能性相等,但出现正、反面的次数不一定相等。
哪面朝上?
做一做
14
1、每小组每人抛硬币1次,抛硬币时用力均匀,高度适中;
2、以小组为单位分别统计相关数据,填入实验报告单 。
3、小组成员分工协作,看哪个小组合作最好,完成得最快!
实验要求:
全班每人掷一次。
朝上的有_____人。
朝上的有_____人。
哪面朝上?
4.思考:正面朝上的次数与总次数有什么样的关系?
做一做
2.
15
五年级1班同学做抛硬币体验的数据
试验小组 抛硬币次数 正面朝上次数 反面朝上次数
第一小组 12 5 7
第二小组 12 6 6
第三小组 12 7 5
第四小组 14 8 6
总计 50 26 24
朝上的可能性大还是 朝上的可能性大?
出现正面和出现反面的可能性是相同的,都是 。
1
2
“可能性”的大小可用分数来表示。
两面朝上的可能性应该是相等的。可为什么出现一个多一个少的现象呢?
虽然可能性相等,但出现正、反面朝上的次数不一定相等。
试验者 抛硬币总次数 正面朝上次数 反面朝上次数
德 摩根 4040 2048 1992
蒲丰 4092 2048 2044
费勒 10000 4979 5021
皮尔逊 12000 6019 5981
皮尔逊 24000 12012 11988
以下是四位数学家做抛币实验的结果
如果抛硬币的次数越多,结果会怎样呢?
抛硬币的次数越多,出现正、反面的朝上的次数越接近。
1.按要求涂一涂。
摸出的一定是 。
摸出的不可能是 。
摸出的可能是 。
必须全部涂蓝色。
答案不唯一,
只要不涂黄色即可。
答案不唯一,
至少有一个涂橘色,
但不能都涂橘色。
(教材第47页第4题)
2.
全班猜一猜。
盒子
人数
1号
2号
3号
4号
只有一枚硬币,可能在哪个盒子里?
猜对的人多,还是猜错的人多?
猜错的可能有3种,猜对的可能有1种,3>1,猜错的可能性大。
(教材第48页第9题)
(教材第49页第10题)
5红面1蓝面, 4红面2蓝面。
4. 给 涂上红、蓝两种颜色,要使掷出红色朝上的可能性比蓝色大,应该怎么涂?
红色的面应比蓝色的面多。
或5红1蓝。
所以可以涂 4红2蓝
共6个面
5.把10张卡片放入纸袋,随意摸一张,要使摸出数字
“1”的可能性最大,数字“5”的可能性最小,卡片上可以是什么数字?请你填一填。
1
1
1
1
1
1
1
1
5
卡片中 “1”的张数要最多;
卡片中 “5”的张数要最少。
(教材第49页第11题)
1
1
1
1
1
1
1
1
1
5
5
1
1
1
1
1
1
1
2
2
5
1
1
1
1
1
1
4
4
4
5
10张卡片中可以只有“1”和“5”两个数字,也可以有其他数字。
5.把10张卡片放入纸袋,随意摸一张,要使摸出数字
“1”的可能性最大,数字“5”的可能性最小,卡片上可以是什么数字?请你填一填。
6.每个盒子中都放着大小相同、颜色不同的10个球,
该怎么放?
(1)任意摸出1个球,摸出红球的可能性大。
(2)任意摸出1个球,一定是红球。
( )个红球
( )个黄球
( )个红球
( )个黄球
1
2
9
1
8
2
7
3
6
4
10
0
(3)任意摸出1个球,摸出红球和黄球的可能性一样大。
(4)任意摸出1个球,不可能是红球。
( )个红球
( )个黄球
( )个红球
( )个黄球
3
4
0
10
5
5
(1)
(2)
7. 小宇要设计一个转盘,上面画着 和 两种图案。如果要达到下面的要求,他该怎么画?
(1)任意转动1次,转到 的可能性大。
(2)任意转动1次,一定转到 。
的数量要多
都是
(答案不唯一)
(3)
(4)
(3)任意转动1次,转到 和 的可能性一样大。
(4)任意转到1次,不可能转到 。
和 的数量一样多
只有 ,没有
7. 小宇设计了一个转盘,上面画有 和 两种图案。宁宁转了20次,结果如右表。
8次 12次
根据表中的数据,小宇设计
的转盘最有可能是 ;不
可能是 。
(1)
(2)
(3)
(1)
(3)
8. 小亮和小强玩摸球游戏(盒子里的球如右图所示)。一次摸 2个球,摸后放回,如果摸到2个红球算小亮赢,摸到1红1蓝,算小强赢,摸到2蓝不分输赢,重摸。他们俩谁获胜的可能性大?
小亮赢的情形只有一种,而小强赢的情形有四种,很明显,小强获胜的可能性大。
1
1
2
1
1
2
1
2
小亮赢:
小强赢:
2
1
2
2
不分输赢:
先给盒子中的球做上标记,比如可以标记为 和 ,再列出他们俩赢的情形。
1
2
1
2
可能性的大小
可能性大小
数量越多
可能性越大
与数量有关
数量越少
可能性越小
概率问题
概率主要研究不确定现象,它起源于博奕问题。15~16世纪,意大利数学家们曾讨论过“如果两人赌博提前结束,该如何分配赌金”等问题。比如,两个人做掷硬币游戏。掷出正面甲得1分,掷出反面乙得1分,先得到10分的人赢得蛋糕,如果游戏因故中途结束,此时甲得了8分,乙得了7分,那么他们该如何分配这个蛋糕呢?
为了回答上述问题,人们对不确定现象进行了大量的研究,前面已列举了历史上一些数学家所做的掷硬币试验的数据。
对不确定现象的研究,最终导致了概率论与数理统计这门学科的出现。它自产生之日起,就与人们的实际生活有着紧密的联系,并且解决了许多科技发展中的问题。正因为如此,这门学科有着很强的生命力和广阔的发展前景。
