第4单元比例培优卷(单元测试含答案)2023-2024学年数学六年级下册人教版
文档属性
| 名称 | 第4单元比例培优卷(单元测试含答案)2023-2024学年数学六年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 483.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第4单元比例培优卷(单元测试)2023-2024学年数学六年级下册人教版
一、选择题
1.下面( )组的两个比不能组成比例。
A.7∶8和14∶16 B.0.6∶0.2和3∶1
C.19∶110和10∶9 D.2.4∶1.6和60∶40
2.图上6厘米表示实际距离240千米,这幅图的比例尺是( )。
A.1∶40000 B.1∶400000 C.1∶4000000 D.1∶40000000
3.在比例尺是1∶1000的校园平面图上,量得学校篮球场的长是2.8cm,宽是1.5cm这个篮球场的实际面积是( )。
A.420平方厘米 B.420平方分米 C.42平方米 D.420平方米
4.下列各种关系中,成正比例关系的是( )。
A.圆锥的底面积一定,圆锥的体积和高
B.平行四边形的面积一定,它的底与高
C.三角形的面积不变,它的底和高
D.圆的半径固定,它的面积与圆周率
5.如果一个圆柱的底面半径是a厘米,高是h厘米,且2∶a=a∶3,这个圆柱的体积是( )立方厘米。
A.πh B.6πh C.6πah D.无法求出
6.如图所示的长方形,甲被分成四个长方形,乙被分成四个三角形,已知其中三个部分的面积,则甲,乙面积相比较,正确的结论是( )。
甲图
A.甲>乙 B.甲=乙 C.甲<乙 D.无法确定
二、填空题
7.根据4.5×4=3.6×5写出一个比例是( )。
8.如果5=6,那么和成( )比例;如果∶3=5∶,那么和成( )比例。
9.在比例尺的地图上。1厘米表示实际距离( )千米,实际距离420千米,在这幅地图上用( )厘米表示。
10.一个长方形精密零件的长为5mm,宽为3.2mm,在一幅图纸上这个零件的长为10cm。那么这幅图纸的比例尺是( ),在这幅图纸上这个零件的面积是( )。
11.为了庆祝六一节每张卡片减价20%,用同样多的钱可以多买6张,原来可以买( )张卡片。
12.在比例尺是1∶4000000的地图上,量得A、B两港距离为3厘米,一艘货轮于上午6时以每小时24千米的速度从A港开往B港,到达B港的时间是( )点。
三、判断题
13.8∶7和14∶16能组成比例。( )
14.一个长方形按1∶4缩小后,周长和面积都缩小到了原来的。( )
15.不是方程。( )
16.仓库有一批货物,每辆车每次运送货物的质量与运送的次数成反比。( )
17.圆锥体的底面半径与π成正比。( )
四、计算题
18.直接写出得数。
1.25×1.6= 28.26÷3.14÷2= 6∶5=( )∶1.5
19.解方程。
5+0.3=5.6 -+3=30 ∶=3∶
五、解答题
20.张爷爷家5月份用电120度,交电费66元,同小区万奶奶家交了82.5元,万奶奶家用电多少度?(用比例解)
21.王老师的身高是1.8米,量得他的影长是1.5米,同时量得学校旗杆的影长是7.5米,学校旗杆高多少米?(用比例解)
22.一间房屋用边长为3分米的地砖铺地需要112块,若改用边长为4分米的地砖铺地需要多少块?(用比例解)
23.在比例尺是1∶3000000的地图上,量得甲市到乙市的距离是30厘米。一辆客车和一辆货车同时从甲、乙两市相对开出,5小时后相遇。已知客车和货车的速度比是5∶4,客车和货车的速度各是多少?
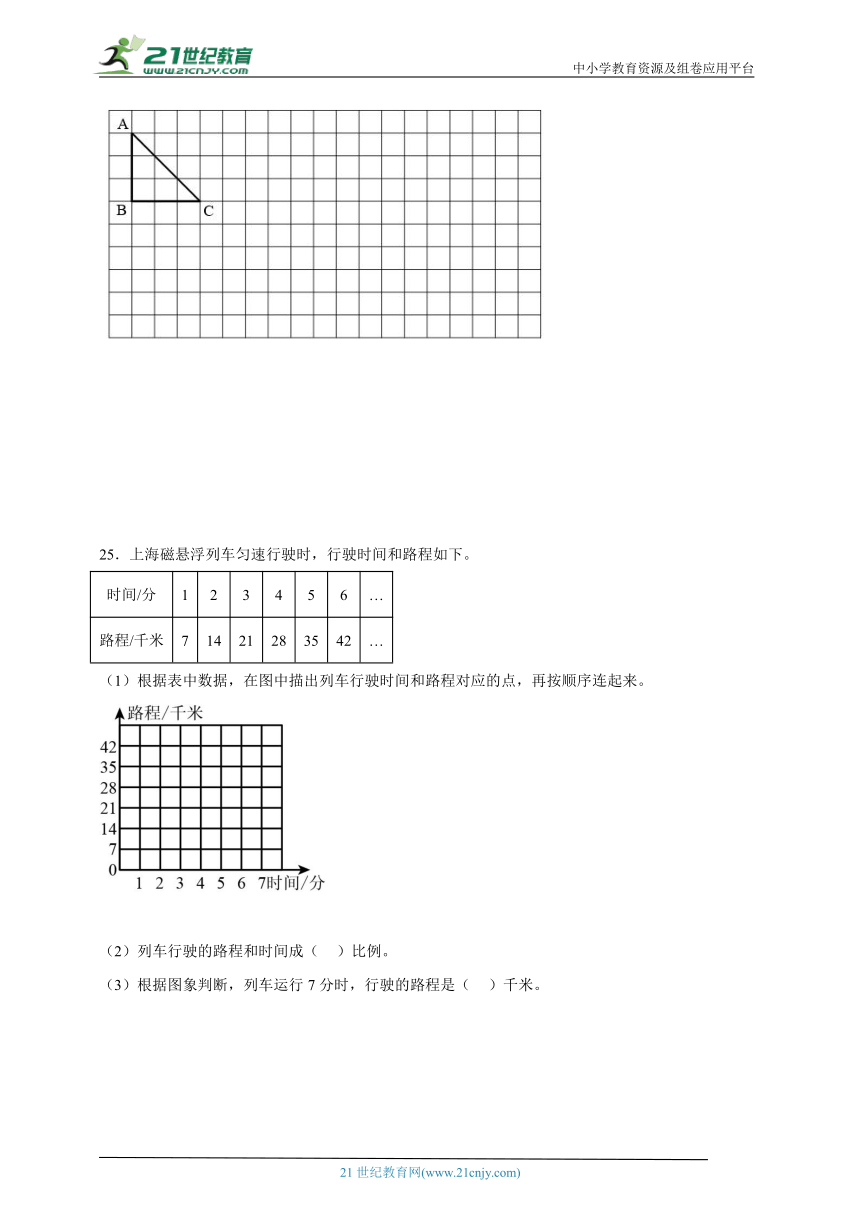
24.画一画,填一填。
(1)仔细观察三角形ABC,C点在A点的( )偏( )( )方向。
(2)画出三角形绕C点顺时针旋转90°后的图形,再把旋转后的图形向右平移2格。
(3)将原三角形按2∶1的比放大,画出放大后的图形。放大后的三角形与原三角形面积的比是( )。
25.上海磁悬浮列车匀速行驶时,行驶时间和路程如下。
时间/分 1 2 3 4 5 6 …
路程/千米 7 14 21 28 35 42 …
(1)根据表中数据,在图中描出列车行驶时间和路程对应的点,再按顺序连起来。
(2)列车行驶的路程和时间成( )比例。
(3)根据图象判断,列车运行7分时,行驶的路程是( )千米。
参考答案:
1.C
【分析】表示两个比相等的式子叫做比例,比例的基本性质:两外项之积等于两内项之积;据此判断即可。
【详解】A.8×14=112
7×16=112
112=112
所以7∶8和14∶16可以组成比例;
B.0.2×3=0.6
0.6×1=0.6
0.6=0.6
所以0.6∶0.2和3∶1可以组成比例;
C.110×10=1100
19×9=171
1100≠171
所以19∶110和10∶9不可以组成比例;
D.1.6×60=96
2.4×40=96
96=96
所以2.4∶1.6和60∶40可以组成比例。
故答案为:C
【点睛】本题考查了比例的认识以及比例的基本性质的应用。
2.C
【分析】先统一单位,然后根据比例尺=图上距离∶实际距离,写出这幅图的比例尺,再化简即可。
【详解】240千米=24000000厘米
6厘米∶24000000厘米
=(6÷6)∶(24000000÷6)
=1∶4000000
这幅图的比例尺是1∶4000000。
故答案为:C
【点睛】本题主要考查了比例尺的意义,要注意统一单位。
3.D
【分析】首先根据实际距离=图上距离÷比例尺,求出实际的长、宽,然后根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】(厘米)
2800厘米=28米
(厘米)
1500厘米=15米
28×15=420(平方米)
故答案为:D
【点睛】此题考查的目的是理解掌握比例尺的意义及应用,以及长方形的面积公式的灵活运用。
4.A
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.根据圆锥的体积公式V=Sh可知,3V÷h=S(一定),即商一定,则圆锥的体积和高成正比例关系;
B.根据平行四边形的面积公式S=ah可知,平行四边形的面积一定,即积一定,则它的底与高成反比例关系;
C.根据三角形的面积公式S=ah÷2可知,三角形的面积一定,即积一定,则它的底和高成反比例关系;
D.根据圆的面积公式S=πr2,其中π是一个定值,r2也一定,则圆的面积一定,所以圆的半径固定时,面积与圆周率不成比例。
故答案为:A
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
5.B
【分析】根据比例的基本性质:两外项之积等于两内项之积,可知a2=2×3,已知一个圆柱的底面半径是a厘米,高是h厘米,根据圆柱的体积公式,用π×2×3×h即可求出这个圆柱的体积。
【详解】如果一个圆柱的底面半径是a厘米,高是h厘米,
且2∶a=a∶3
则a2
=2×3
=6(平方厘米)
圆柱的体积:π×6×h=6πh(立方厘米)
这个圆柱的体积是6πh立方厘米。
故答案为:B
【点睛】本题主要考查了比例的基本性质的应用以及圆柱的体积公式的灵活应用。
6.A
【分析】由长方形的面积=长×宽,可知等宽的两个长方形面积的比等于长的比,根据这个等量关系列出比例求甲图面积;
根据等底等高的三角形面积是长方形面积的一半可得乙图面积=(10+24)的2倍,依此可求乙图面积。
【详解】根据长方形的性质,得18和10所在的长方形的长的比是9:5。
解:设要求的第四块的面积是x平方厘米。
x:15=9:5
5x=135
5x÷5=135÷5
x=27
18+10+27+15=70
故甲图面积是70,
(10+24)×2
=34×2
=68
故乙图面积是68,
因为70>68,所以甲>乙。
故答案为:A
【点睛】此题主要是找到等宽的两个长方形,根据面积的比等于长的比进行求解。同时考查了等底等高的三角形面积是长方形面积的一半的知识点。
7.5∶4=4.5∶3.6
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积;据此解答。
【详解】根据4.5×4=3.6×5写出一个比例是5∶4=4.5∶3.6。
(答案不唯一)
【点睛】解答此题的关键是比例基本性质的逆运用,要注意:相乘的两个数要做外项就都做外项,要做内项就都做内项。
8. 正 反
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】如果5=6,则=(一定),比值一定,那么和成正比例;
如果∶3=5∶,则=3×5=15(一定),乘积一定,那么和成反比例。
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
9. 30 14
【分析】由线段比例尺可知,图上1厘米代表实际距离30千米,根据“比例尺=图上距离∶实际距离”求出数值比例尺,最后利用“图上距离=实际距离×比例尺”求出在这幅地图上的图上距离,据此解答。
【详解】图上1厘米表示实际距离30千米;
1厘米∶30千米
=1厘米∶3000000厘米
=1∶3000000
420千米=42000000厘米
42000000×=14(厘米)
即实际距离420千米在这幅地图上用14厘米表示。
【点睛】掌握比例尺的意义以及图上距离和实际距离换算的方法是解答题目的关键。
10. 20∶1 64cm2
【分析】已知长方形零件长的图上尺寸和实际尺寸,根据“比例尺=图上距离∶实际距离”,以及进率1cm=10mm,求出这幅图纸的比例尺。
已知长方形零件宽的实际尺寸,根据“图上距离=实际距离×比例尺”,求出宽的图上尺寸;
根据长方形的面积=长×宽,代入数据计算,即可求出这个零件的图上面积。
【详解】10cm∶5mm
=(10×10)mm∶5mm
=100∶5
=(100÷5)∶(5÷5)
=20∶1
宽的图上尺寸:
3.2×=64(mm)
64mm=6.4cm
零件的图上面积:10×6.4=64(cm2)
这幅图纸的比例尺是20∶1,在这幅图纸上这个零件的面积是64cm2。
【点睛】本题考查比例尺的意义以及长方形面积公式的运用,掌握图上距离、实际距离、比例尺之间的关系是解题的关键。
11.24
【分析】先设原来卡片的单价是1,把原来卡片的单价看作单位“1”,现在每张卡片减价20%,则现在每张卡片的价格是原来的(1-20%),用原价乘(1-20%),求出现在每张卡片的价格;
根据“用同样多的钱”可知,总钱数不变,即单价×数量=总价(一定),乘积一定,则单价和数量成反比例关系,据此列出反比例方程,并求解。
【详解】设原来卡片的单价是1,现在卡片的单价是:
1×(1-20%)
=1×0.8
=0.8
解:设原来可以买张卡片。
1×=0.8×(+6)
=0.8+4.8
-0.8=4.8
0.2=4.8
=4.8÷0.2
=24
原来可以买24张卡片。
【点睛】先确定总钱数不变,再根据单价、数量、总价之间的关系,得出单价和数量成反比例关系,据此列出相应的比例方程。
12.11
【分析】先根据“图上距离÷比例尺=实际距离”,代入数据求出A、B两港的实际距离,再根据路程÷速度=时间,求出从A港开往B港的经过时间,利用“开始时间+经过时间=结束时间”,即可求出到达B港的时间。
【详解】3÷
=3×4000000
=12000000(厘米)
=120(千米)
120÷24=5(小时)
上午6时+5小时=上午11时。
即到达B港的时间是11点。
【点睛】此题主要考查图上距离和实际距离之间的换算、普通行程问题以及24时计时法时间的计算。
13.×
【分析】计算两个比的比值,表示两个比相等的式子叫做比例,据此解答。
【详解】8∶7=,14∶16=,因为≠,所以8∶7和14∶16不能组成比例。
故答案为:×
【点睛】掌握比例的意义是解答题目的关键。
14.×
【分析】图形放大或缩小后,对应边长度的比相等,周长的比也相等,但面积的比不相等,据此解答。
【详解】一个长方形按1∶4缩小后,周长缩小到原来的,面积缩小到原来的=。
故答案为:×
【点睛】把图形按1∶n缩小后,周长缩小到原来的,面积缩小到原来的。
15.×
【分析】方程是含有未知数的等式,据此判断。
【详解】既含有未知数x,又是用等号连接的式子,所以它是方程。
故答案为:×
【点睛】本题考查方程的定义。
16.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为每次运送货物的质量运送的次数一批货物的总质重(一定),是乘积一定,所以每辆车每次运送货物的质量与运送的次数成反比。
故答案为:√
【点睛】此题属于辨识成正、反比例关系的量的题目,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
17.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】圆锥的体积公式:
得到,题目中并没说体积一定,而且本身就是一定的,所以圆锥体的底面半径与π不成比例。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
18.2;4.5;0.0942;1.8
【详解】略
19.=2;=36;=
【分析】(1)方程两边先同时减去5,再同时除以0.3,求出方程的解;
(2)先计算方程左边的-,把方程化简成+3=30,然后方程两边先同时减去3,再同时除以,求出方程的解;
(3)先根据比例的基本性质将比例方程改写成=×3,然后方程两边同时除以,求出方程的解。
【详解】(1)5+0.3=5.6
解:5+0.3-5=5.6-5
0.3=0.6
0.3÷0.3=0.6÷0.3
=2
(2)-+3=30
解:+3=30
+3-3=30-3
=27
÷=27÷
=27×
=36
(3)∶=3∶
解:=×3
=
÷=÷
=×
=
20.150度
【分析】由题意可知:电费的单价是一定的,即电费与用电量的比值是一定的,则电费与用电量成正比例,据此即可列比例求解。
【详解】解:设万奶奶家用电x度,
66∶120=82.5∶x
66x=120×82.5
66x=9900
x=9900÷66
x=150
答:万奶奶家用电150度。
【点睛】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
21.9米
【分析】根据题意可知,物体的长度和它影子的长度的比值一定,即物体的长度和它影子的长度成正比例,设学校旗杆高x米,由此解比例即可。
【详解】解:设学校旗杆高米。
1.5x=1.8×7.5
1.5x=13.5
1.5x÷1.5=13.5÷1.5
答:学校旗杆高9米。
【点睛】本题考查了用比例解决问题,注意判断两个相关联的量成正比例还是反比例。
22.63块
【分析】正方形面积=边长×边长,设改用边长为4分米的地砖铺地需要x块,根据每块地砖的面积×块数=房屋面积(一定),列出反比例算式解答即可。
【详解】解:设改用边长为4分米的地砖铺地需要x块。
4×4×x=3×3×112
16x=1008
16x÷16=1008÷16
x=63
答:若改用边长为4分米的地砖铺地需要63块。
【点睛】关键是理解反比例的意义,积一定是反比例关系。
23.100千米/小时;80千米/小时
【分析】
根据“实际距离=图上距离÷比例尺”,把数据代入求出甲市、乙市两地的实际距离,根据关系式“路程÷相遇时间=速度和”,先求出客车和货车的速度和,然后按比例分配的方法,分别求出客车和货车的速度各是多少。
【详解】30÷
=30×3000000
=90000000(厘米)
=900(千米)
900÷5=180(千米/小时)
180×
=180×
=100(千米/小时)
180×
=180×
=80(千米/小时)
答:客车的速度是100千米/小时,货车的速度是80千米/小时。
【点睛】此题的解题关键是利用图上距离和实际距离之间换算的方法,再根据路程、相遇时间和速度之和三者之间的关系及按比例分配知识进行解答。
24.(1)南;东;45°;
(2)见详解;
(3)见详解;4∶1
【分析】(1)三角形ABC是等腰直角三角形,∠BAC=∠BCA=45°,以A点为观测点,根据“上北下南,左西右东”结合角度描述方向,C点在A点正南方向偏东45°方向;
(2)根据题目要求确定旋转中心(C点)、旋转方向(顺时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形,据此画出旋转后的图形;找出构成图形的关键点,确定平移方向(向右)和平移距离(2格),由平移的距离确定关键点平移后的对应点的位置;依次连接各对应点,据此画出平移后的图形;
(3)原来等腰直角三角形的直角边是3格,放大后等腰直角三角形的直角边是3×2=6格,据此画出放大后的图形,再根据“三角形的面积=底×高÷2”求出原来和现在三角形的面积,最后求出放大后的三角形与原来三角形的面积比,据此解答。
【详解】(1)分析可知,C点在A点的南偏东45°方向。
(2)作图如下:
(3)假设小正方形的边长为1。
原来三角形的面积:3×3÷2=
现在三角形的面积:6×6÷2=18
现在三角形的面积∶原来三角形的面积
=18∶
=(18×2)∶(×2)
=36∶9
=(36÷9)∶(9÷9)
=4∶1
所以,放大后的三角形与原三角形面积的比是4∶1。
【点睛】掌握平移、旋转、放大图形的作图方法,并熟记三角形的面积计算公式是解答题目的关键。
25.(1)见详解;
(2)正;
(3)49
【分析】(1)由图可知,图中横轴表示时间,纵轴表示路程,单位长度表示7千米,根据表格中的数据描出各点,再依次连接各点;
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
(3)由“路程=速度×时间”可知,列车每分钟行驶7千米,7分钟行驶7×7=49(千米),据此解答。
【详解】(1)分析可知:
(2)=======…=7(一定)
所以,列车行驶的路程和时间成正比例。
(3)7×7=49(千米)
观察图象可知,列车运行7分时,行驶的路程是49千米。
【点睛】本题主要考查正比例关系的辨识,掌握正比例关系的意义是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第4单元比例培优卷(单元测试)2023-2024学年数学六年级下册人教版
一、选择题
1.下面( )组的两个比不能组成比例。
A.7∶8和14∶16 B.0.6∶0.2和3∶1
C.19∶110和10∶9 D.2.4∶1.6和60∶40
2.图上6厘米表示实际距离240千米,这幅图的比例尺是( )。
A.1∶40000 B.1∶400000 C.1∶4000000 D.1∶40000000
3.在比例尺是1∶1000的校园平面图上,量得学校篮球场的长是2.8cm,宽是1.5cm这个篮球场的实际面积是( )。
A.420平方厘米 B.420平方分米 C.42平方米 D.420平方米
4.下列各种关系中,成正比例关系的是( )。
A.圆锥的底面积一定,圆锥的体积和高
B.平行四边形的面积一定,它的底与高
C.三角形的面积不变,它的底和高
D.圆的半径固定,它的面积与圆周率
5.如果一个圆柱的底面半径是a厘米,高是h厘米,且2∶a=a∶3,这个圆柱的体积是( )立方厘米。
A.πh B.6πh C.6πah D.无法求出
6.如图所示的长方形,甲被分成四个长方形,乙被分成四个三角形,已知其中三个部分的面积,则甲,乙面积相比较,正确的结论是( )。
甲图
A.甲>乙 B.甲=乙 C.甲<乙 D.无法确定
二、填空题
7.根据4.5×4=3.6×5写出一个比例是( )。
8.如果5=6,那么和成( )比例;如果∶3=5∶,那么和成( )比例。
9.在比例尺的地图上。1厘米表示实际距离( )千米,实际距离420千米,在这幅地图上用( )厘米表示。
10.一个长方形精密零件的长为5mm,宽为3.2mm,在一幅图纸上这个零件的长为10cm。那么这幅图纸的比例尺是( ),在这幅图纸上这个零件的面积是( )。
11.为了庆祝六一节每张卡片减价20%,用同样多的钱可以多买6张,原来可以买( )张卡片。
12.在比例尺是1∶4000000的地图上,量得A、B两港距离为3厘米,一艘货轮于上午6时以每小时24千米的速度从A港开往B港,到达B港的时间是( )点。
三、判断题
13.8∶7和14∶16能组成比例。( )
14.一个长方形按1∶4缩小后,周长和面积都缩小到了原来的。( )
15.不是方程。( )
16.仓库有一批货物,每辆车每次运送货物的质量与运送的次数成反比。( )
17.圆锥体的底面半径与π成正比。( )
四、计算题
18.直接写出得数。
1.25×1.6= 28.26÷3.14÷2= 6∶5=( )∶1.5
19.解方程。
5+0.3=5.6 -+3=30 ∶=3∶
五、解答题
20.张爷爷家5月份用电120度,交电费66元,同小区万奶奶家交了82.5元,万奶奶家用电多少度?(用比例解)
21.王老师的身高是1.8米,量得他的影长是1.5米,同时量得学校旗杆的影长是7.5米,学校旗杆高多少米?(用比例解)
22.一间房屋用边长为3分米的地砖铺地需要112块,若改用边长为4分米的地砖铺地需要多少块?(用比例解)
23.在比例尺是1∶3000000的地图上,量得甲市到乙市的距离是30厘米。一辆客车和一辆货车同时从甲、乙两市相对开出,5小时后相遇。已知客车和货车的速度比是5∶4,客车和货车的速度各是多少?
24.画一画,填一填。
(1)仔细观察三角形ABC,C点在A点的( )偏( )( )方向。
(2)画出三角形绕C点顺时针旋转90°后的图形,再把旋转后的图形向右平移2格。
(3)将原三角形按2∶1的比放大,画出放大后的图形。放大后的三角形与原三角形面积的比是( )。
25.上海磁悬浮列车匀速行驶时,行驶时间和路程如下。
时间/分 1 2 3 4 5 6 …
路程/千米 7 14 21 28 35 42 …
(1)根据表中数据,在图中描出列车行驶时间和路程对应的点,再按顺序连起来。
(2)列车行驶的路程和时间成( )比例。
(3)根据图象判断,列车运行7分时,行驶的路程是( )千米。
参考答案:
1.C
【分析】表示两个比相等的式子叫做比例,比例的基本性质:两外项之积等于两内项之积;据此判断即可。
【详解】A.8×14=112
7×16=112
112=112
所以7∶8和14∶16可以组成比例;
B.0.2×3=0.6
0.6×1=0.6
0.6=0.6
所以0.6∶0.2和3∶1可以组成比例;
C.110×10=1100
19×9=171
1100≠171
所以19∶110和10∶9不可以组成比例;
D.1.6×60=96
2.4×40=96
96=96
所以2.4∶1.6和60∶40可以组成比例。
故答案为:C
【点睛】本题考查了比例的认识以及比例的基本性质的应用。
2.C
【分析】先统一单位,然后根据比例尺=图上距离∶实际距离,写出这幅图的比例尺,再化简即可。
【详解】240千米=24000000厘米
6厘米∶24000000厘米
=(6÷6)∶(24000000÷6)
=1∶4000000
这幅图的比例尺是1∶4000000。
故答案为:C
【点睛】本题主要考查了比例尺的意义,要注意统一单位。
3.D
【分析】首先根据实际距离=图上距离÷比例尺,求出实际的长、宽,然后根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】(厘米)
2800厘米=28米
(厘米)
1500厘米=15米
28×15=420(平方米)
故答案为:D
【点睛】此题考查的目的是理解掌握比例尺的意义及应用,以及长方形的面积公式的灵活运用。
4.A
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.根据圆锥的体积公式V=Sh可知,3V÷h=S(一定),即商一定,则圆锥的体积和高成正比例关系;
B.根据平行四边形的面积公式S=ah可知,平行四边形的面积一定,即积一定,则它的底与高成反比例关系;
C.根据三角形的面积公式S=ah÷2可知,三角形的面积一定,即积一定,则它的底和高成反比例关系;
D.根据圆的面积公式S=πr2,其中π是一个定值,r2也一定,则圆的面积一定,所以圆的半径固定时,面积与圆周率不成比例。
故答案为:A
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
5.B
【分析】根据比例的基本性质:两外项之积等于两内项之积,可知a2=2×3,已知一个圆柱的底面半径是a厘米,高是h厘米,根据圆柱的体积公式,用π×2×3×h即可求出这个圆柱的体积。
【详解】如果一个圆柱的底面半径是a厘米,高是h厘米,
且2∶a=a∶3
则a2
=2×3
=6(平方厘米)
圆柱的体积:π×6×h=6πh(立方厘米)
这个圆柱的体积是6πh立方厘米。
故答案为:B
【点睛】本题主要考查了比例的基本性质的应用以及圆柱的体积公式的灵活应用。
6.A
【分析】由长方形的面积=长×宽,可知等宽的两个长方形面积的比等于长的比,根据这个等量关系列出比例求甲图面积;
根据等底等高的三角形面积是长方形面积的一半可得乙图面积=(10+24)的2倍,依此可求乙图面积。
【详解】根据长方形的性质,得18和10所在的长方形的长的比是9:5。
解:设要求的第四块的面积是x平方厘米。
x:15=9:5
5x=135
5x÷5=135÷5
x=27
18+10+27+15=70
故甲图面积是70,
(10+24)×2
=34×2
=68
故乙图面积是68,
因为70>68,所以甲>乙。
故答案为:A
【点睛】此题主要是找到等宽的两个长方形,根据面积的比等于长的比进行求解。同时考查了等底等高的三角形面积是长方形面积的一半的知识点。
7.5∶4=4.5∶3.6
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积;据此解答。
【详解】根据4.5×4=3.6×5写出一个比例是5∶4=4.5∶3.6。
(答案不唯一)
【点睛】解答此题的关键是比例基本性质的逆运用,要注意:相乘的两个数要做外项就都做外项,要做内项就都做内项。
8. 正 反
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】如果5=6,则=(一定),比值一定,那么和成正比例;
如果∶3=5∶,则=3×5=15(一定),乘积一定,那么和成反比例。
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
9. 30 14
【分析】由线段比例尺可知,图上1厘米代表实际距离30千米,根据“比例尺=图上距离∶实际距离”求出数值比例尺,最后利用“图上距离=实际距离×比例尺”求出在这幅地图上的图上距离,据此解答。
【详解】图上1厘米表示实际距离30千米;
1厘米∶30千米
=1厘米∶3000000厘米
=1∶3000000
420千米=42000000厘米
42000000×=14(厘米)
即实际距离420千米在这幅地图上用14厘米表示。
【点睛】掌握比例尺的意义以及图上距离和实际距离换算的方法是解答题目的关键。
10. 20∶1 64cm2
【分析】已知长方形零件长的图上尺寸和实际尺寸,根据“比例尺=图上距离∶实际距离”,以及进率1cm=10mm,求出这幅图纸的比例尺。
已知长方形零件宽的实际尺寸,根据“图上距离=实际距离×比例尺”,求出宽的图上尺寸;
根据长方形的面积=长×宽,代入数据计算,即可求出这个零件的图上面积。
【详解】10cm∶5mm
=(10×10)mm∶5mm
=100∶5
=(100÷5)∶(5÷5)
=20∶1
宽的图上尺寸:
3.2×=64(mm)
64mm=6.4cm
零件的图上面积:10×6.4=64(cm2)
这幅图纸的比例尺是20∶1,在这幅图纸上这个零件的面积是64cm2。
【点睛】本题考查比例尺的意义以及长方形面积公式的运用,掌握图上距离、实际距离、比例尺之间的关系是解题的关键。
11.24
【分析】先设原来卡片的单价是1,把原来卡片的单价看作单位“1”,现在每张卡片减价20%,则现在每张卡片的价格是原来的(1-20%),用原价乘(1-20%),求出现在每张卡片的价格;
根据“用同样多的钱”可知,总钱数不变,即单价×数量=总价(一定),乘积一定,则单价和数量成反比例关系,据此列出反比例方程,并求解。
【详解】设原来卡片的单价是1,现在卡片的单价是:
1×(1-20%)
=1×0.8
=0.8
解:设原来可以买张卡片。
1×=0.8×(+6)
=0.8+4.8
-0.8=4.8
0.2=4.8
=4.8÷0.2
=24
原来可以买24张卡片。
【点睛】先确定总钱数不变,再根据单价、数量、总价之间的关系,得出单价和数量成反比例关系,据此列出相应的比例方程。
12.11
【分析】先根据“图上距离÷比例尺=实际距离”,代入数据求出A、B两港的实际距离,再根据路程÷速度=时间,求出从A港开往B港的经过时间,利用“开始时间+经过时间=结束时间”,即可求出到达B港的时间。
【详解】3÷
=3×4000000
=12000000(厘米)
=120(千米)
120÷24=5(小时)
上午6时+5小时=上午11时。
即到达B港的时间是11点。
【点睛】此题主要考查图上距离和实际距离之间的换算、普通行程问题以及24时计时法时间的计算。
13.×
【分析】计算两个比的比值,表示两个比相等的式子叫做比例,据此解答。
【详解】8∶7=,14∶16=,因为≠,所以8∶7和14∶16不能组成比例。
故答案为:×
【点睛】掌握比例的意义是解答题目的关键。
14.×
【分析】图形放大或缩小后,对应边长度的比相等,周长的比也相等,但面积的比不相等,据此解答。
【详解】一个长方形按1∶4缩小后,周长缩小到原来的,面积缩小到原来的=。
故答案为:×
【点睛】把图形按1∶n缩小后,周长缩小到原来的,面积缩小到原来的。
15.×
【分析】方程是含有未知数的等式,据此判断。
【详解】既含有未知数x,又是用等号连接的式子,所以它是方程。
故答案为:×
【点睛】本题考查方程的定义。
16.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为每次运送货物的质量运送的次数一批货物的总质重(一定),是乘积一定,所以每辆车每次运送货物的质量与运送的次数成反比。
故答案为:√
【点睛】此题属于辨识成正、反比例关系的量的题目,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
17.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】圆锥的体积公式:
得到,题目中并没说体积一定,而且本身就是一定的,所以圆锥体的底面半径与π不成比例。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
18.2;4.5;0.0942;1.8
【详解】略
19.=2;=36;=
【分析】(1)方程两边先同时减去5,再同时除以0.3,求出方程的解;
(2)先计算方程左边的-,把方程化简成+3=30,然后方程两边先同时减去3,再同时除以,求出方程的解;
(3)先根据比例的基本性质将比例方程改写成=×3,然后方程两边同时除以,求出方程的解。
【详解】(1)5+0.3=5.6
解:5+0.3-5=5.6-5
0.3=0.6
0.3÷0.3=0.6÷0.3
=2
(2)-+3=30
解:+3=30
+3-3=30-3
=27
÷=27÷
=27×
=36
(3)∶=3∶
解:=×3
=
÷=÷
=×
=
20.150度
【分析】由题意可知:电费的单价是一定的,即电费与用电量的比值是一定的,则电费与用电量成正比例,据此即可列比例求解。
【详解】解:设万奶奶家用电x度,
66∶120=82.5∶x
66x=120×82.5
66x=9900
x=9900÷66
x=150
答:万奶奶家用电150度。
【点睛】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
21.9米
【分析】根据题意可知,物体的长度和它影子的长度的比值一定,即物体的长度和它影子的长度成正比例,设学校旗杆高x米,由此解比例即可。
【详解】解:设学校旗杆高米。
1.5x=1.8×7.5
1.5x=13.5
1.5x÷1.5=13.5÷1.5
答:学校旗杆高9米。
【点睛】本题考查了用比例解决问题,注意判断两个相关联的量成正比例还是反比例。
22.63块
【分析】正方形面积=边长×边长,设改用边长为4分米的地砖铺地需要x块,根据每块地砖的面积×块数=房屋面积(一定),列出反比例算式解答即可。
【详解】解:设改用边长为4分米的地砖铺地需要x块。
4×4×x=3×3×112
16x=1008
16x÷16=1008÷16
x=63
答:若改用边长为4分米的地砖铺地需要63块。
【点睛】关键是理解反比例的意义,积一定是反比例关系。
23.100千米/小时;80千米/小时
【分析】
根据“实际距离=图上距离÷比例尺”,把数据代入求出甲市、乙市两地的实际距离,根据关系式“路程÷相遇时间=速度和”,先求出客车和货车的速度和,然后按比例分配的方法,分别求出客车和货车的速度各是多少。
【详解】30÷
=30×3000000
=90000000(厘米)
=900(千米)
900÷5=180(千米/小时)
180×
=180×
=100(千米/小时)
180×
=180×
=80(千米/小时)
答:客车的速度是100千米/小时,货车的速度是80千米/小时。
【点睛】此题的解题关键是利用图上距离和实际距离之间换算的方法,再根据路程、相遇时间和速度之和三者之间的关系及按比例分配知识进行解答。
24.(1)南;东;45°;
(2)见详解;
(3)见详解;4∶1
【分析】(1)三角形ABC是等腰直角三角形,∠BAC=∠BCA=45°,以A点为观测点,根据“上北下南,左西右东”结合角度描述方向,C点在A点正南方向偏东45°方向;
(2)根据题目要求确定旋转中心(C点)、旋转方向(顺时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形,据此画出旋转后的图形;找出构成图形的关键点,确定平移方向(向右)和平移距离(2格),由平移的距离确定关键点平移后的对应点的位置;依次连接各对应点,据此画出平移后的图形;
(3)原来等腰直角三角形的直角边是3格,放大后等腰直角三角形的直角边是3×2=6格,据此画出放大后的图形,再根据“三角形的面积=底×高÷2”求出原来和现在三角形的面积,最后求出放大后的三角形与原来三角形的面积比,据此解答。
【详解】(1)分析可知,C点在A点的南偏东45°方向。
(2)作图如下:
(3)假设小正方形的边长为1。
原来三角形的面积:3×3÷2=
现在三角形的面积:6×6÷2=18
现在三角形的面积∶原来三角形的面积
=18∶
=(18×2)∶(×2)
=36∶9
=(36÷9)∶(9÷9)
=4∶1
所以,放大后的三角形与原三角形面积的比是4∶1。
【点睛】掌握平移、旋转、放大图形的作图方法,并熟记三角形的面积计算公式是解答题目的关键。
25.(1)见详解;
(2)正;
(3)49
【分析】(1)由图可知,图中横轴表示时间,纵轴表示路程,单位长度表示7千米,根据表格中的数据描出各点,再依次连接各点;
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
(3)由“路程=速度×时间”可知,列车每分钟行驶7千米,7分钟行驶7×7=49(千米),据此解答。
【详解】(1)分析可知:
(2)=======…=7(一定)
所以,列车行驶的路程和时间成正比例。
(3)7×7=49(千米)
观察图象可知,列车运行7分时,行驶的路程是49千米。
【点睛】本题主要考查正比例关系的辨识,掌握正比例关系的意义是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
