五年级数学上册(人教版)第三单元 第6课时 商的近似值(课件)(共29张PPT)
文档属性
| 名称 | 五年级数学上册(人教版)第三单元 第6课时 商的近似值(课件)(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 14:10:31 | ||
图片预览

文档简介
(共29张PPT)
小数除法
人教版五年级数学上册
第6课时 商的近似数
3
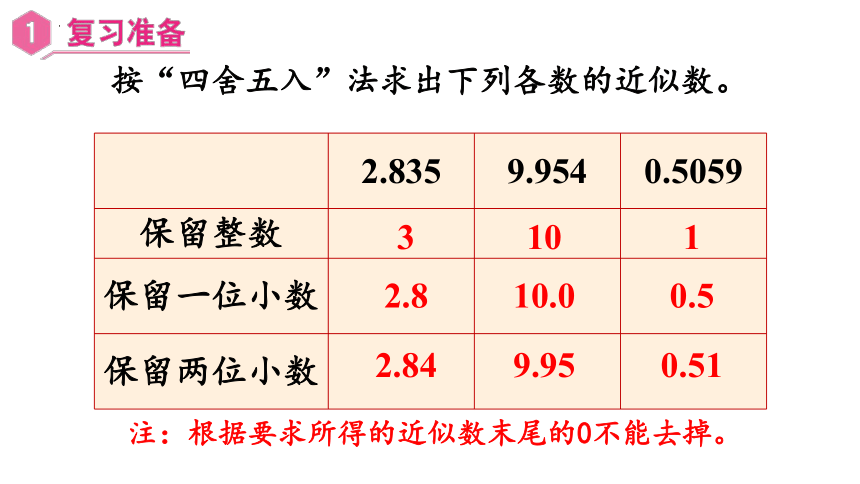
按“四舍五入”法求出下列各数的近似数。
2.835 9.954 0.5059
保留整数
保留一位小数
保留两位小数
2.8
10.0
0.5
3
10
1
2.84
9.95
0.51
注:根据要求所得的近似数末尾的0不能去掉。
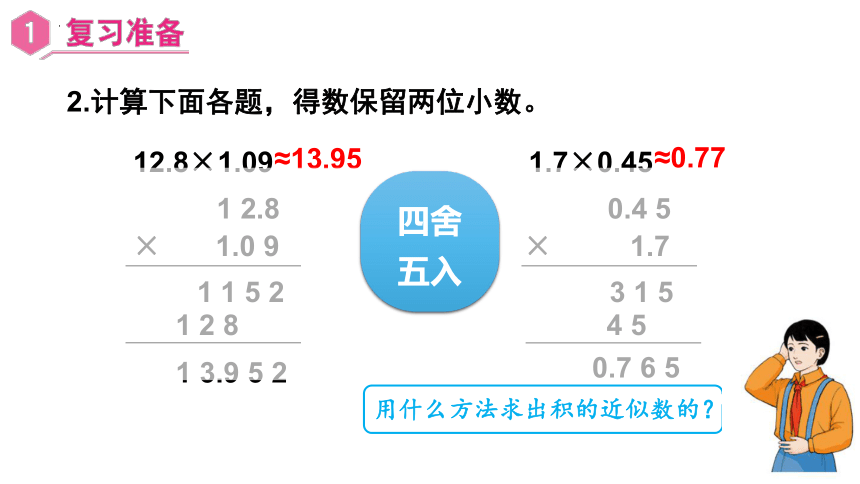
2.计算下面各题,得数保留两位小数。
12.8×1.09
1.7×0.45
≈13.95
≈0.77
1 2.8
1.0 9
×
1 1 5 2
1 2 8
1 3.9 5 2
0.4 5
1.7
×
3 1 5
4 5
0.7 6 5
用什么方法求出积的近似数的?
四舍五入
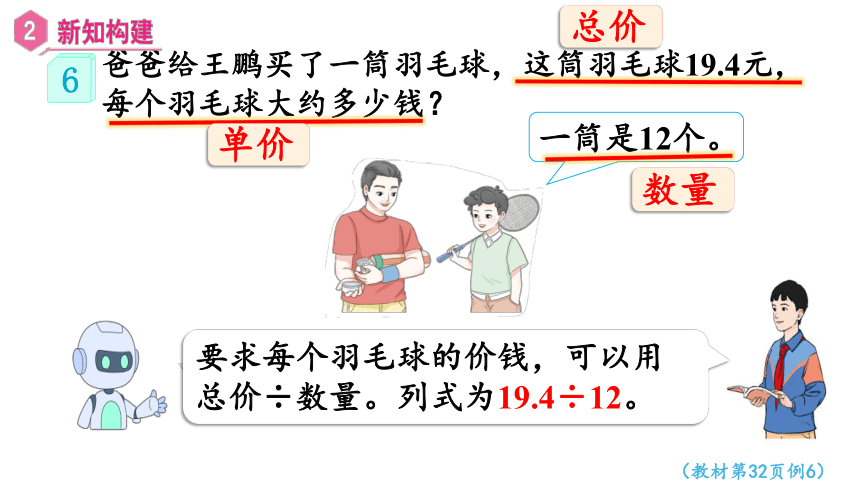
爸爸给王鹏买了一筒羽毛球,这筒羽毛球19.4元,每个羽毛球大约多少钱?
(教材第32页例6)
一筒是12个。
从题目中你获得了哪些条件?
要求什么问题?
要求每个羽毛球的价钱,可以用总价÷数量。列式为19.4÷12。
总价
数量
单价
6
一筒是12个。
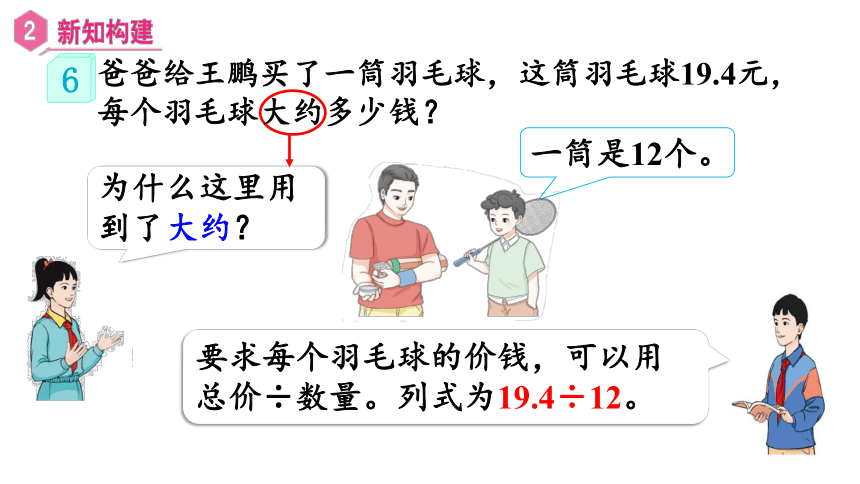
为什么这里用到了大约?
要求每个羽毛球的价钱,可以用总价÷数量。列式为19.4÷12。
爸爸给王鹏买了一筒羽毛球,这筒羽毛球19.4元,每个羽毛球大约多少钱?
6
爸爸给王鹏买了一筒羽毛球,这筒羽毛球19.4元,每个羽毛球大约多少钱?
那怎么求商的近似数呢?
可以先算出19.4÷12的商,然后按“四舍五入” 法取近似数。
一筒是12个。
6
1 9.4
12
1
1 2
7
4
6
7 2
2
0
1
1 2
8
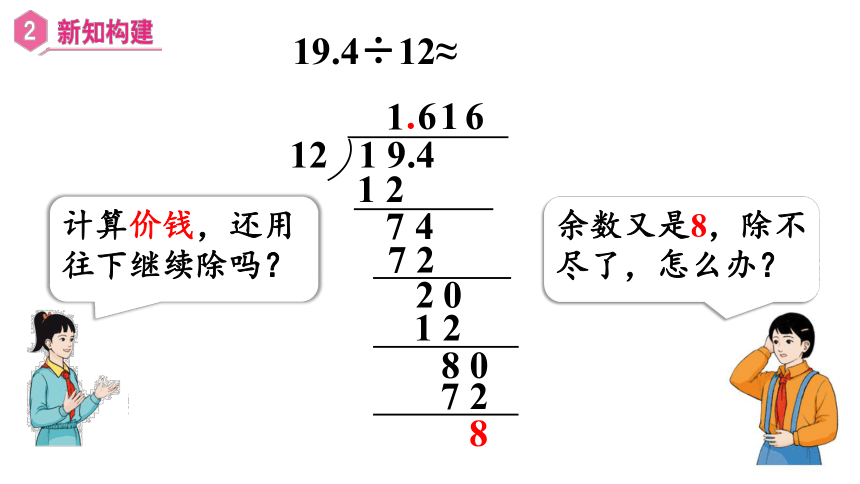
余数又是8,除不尽了,怎么办?
计算价钱,还用往下继续除吗?
.
0
6
7 2
8
19.4÷12≈
1 9.4
12
1
1 2
7
4
6
7 2
2
0
1
1 2
8
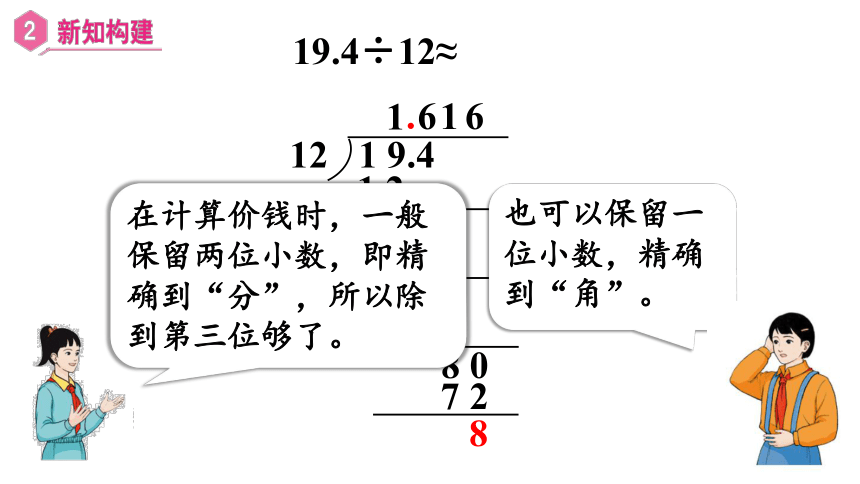
也可以保留一位小数,精确到“角”。
在计算价钱时,一般保留两位小数,即精确到“分”,所以除到第三位够了。
.
0
6
7 2
8
19.4÷12≈
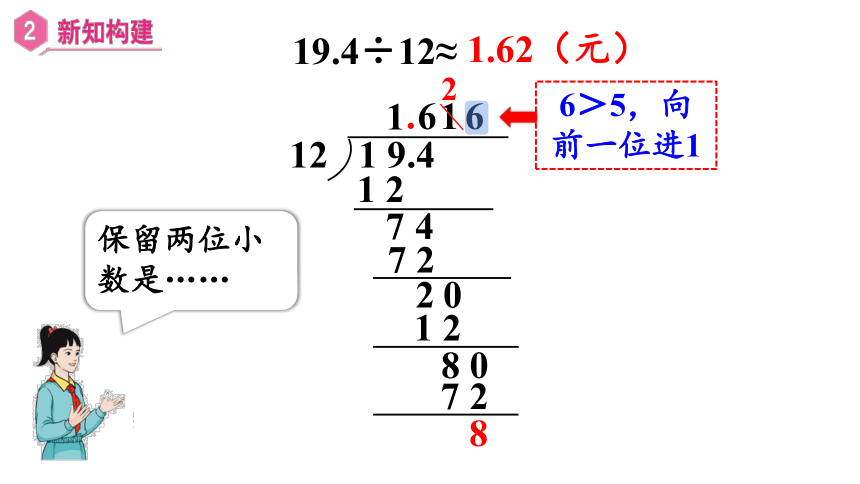
19.4÷12≈
1 9.4
12
1
1 2
7
4
6
7 2
2
0
1
1 2
8
.
0
6
7 2
8
6>5,向前一位进1
2
1.62(元)
保留两位小数是……
19.4÷12≈
1 9.4
12
1
1 2
7
4
6
7 2
2
0
1
1 2
8
.
0
6
7 2
8
1.6(元)
1<5,舍去
那保留一位小数除到第二位也行了。
保留一位小数是……
爸爸给王鹏新买了一筒羽毛球。
一筒是12个。
问题延伸
这筒羽毛球19.4 元,每个大约多少钱?
86
要求每个羽毛球的价钱,可以用总价÷数量。列式为19.86÷12。
19.86÷12
1 9. 8 6
12
1
1 2
7
8
6
7 2
6
6
5
6 0
6
.
0
5
6 0
0
能除尽,还用保留近似数吗?
虽然能除尽,但此题计算的是钱数,最多只能保留两位小数。
19.86÷12
1 9. 8 6
12
1
1 2
7
8
6
7 2
6
6
5
6 0
6
.
0
5
6 0
0
保留一位小数是……
5=5,向前一位进1
2
≈1.62(元)
保留两位小数是……
5=5,向前一位进1
7
≈1.7(元)
怎么求商的近似数?保留到哪一位比较合适?
求商的近似数时,计算到比保留的小数位多一位,再将最后一位“四舍五入”。
怎么求商的近似数?保留到哪一位比较合适?
看——需要保留几位小数;
归纳:
除——除到比需要保留的小数位数多一位;
取——将最后一位“四舍五入”取商的近似值。
9.5
2.6
7 8
6.8×0.37 ≈
2.5
(保留一位小数)
9.5÷2.6 ≈
3.8
算一算,比一比,求积和商的近似值时有什么异同?
6.8
0.3 7
4 7 6
2 0 4
2 5 1 6
.
3
.
0
8
1 7
0
1 6 8
2
0
×
(保留一位小数)
6.8×0.37 ≈
2.5
9.5÷2.6 ≈
3.8
算一算,比一比,求积和商的近似值时有什么异同?
相同点:都是按照“四舍五入”法取近似值的。
不同点
求积的近似值必须算出整个积才能取近似值。
求商的近似值时只要计算出比要求保留的小数多一位小数就可以了。
(保留一位小数)
(保留一位小数)
我发现:在计算小数除法需要求商的近似数时,一般除到比需要保留的小数位数多( 一 )位,再按照( 四舍五)法取商的近似数。保留小数位数,需要连续进位时,近似数末尾的0
( 不能 )(填“能”或“不能”)去掉。
一
四舍五入
不能
求商的近似数的方法
4.8÷2.3 (保留一位小数)
.
0
4 8
2.3
2
4 6
2
0
0
1 6
1 8 4
0
0
8
≈2.1
1.计算下面各题。
.
(教材第32页“做一做”)
做一做
1.55÷3.9 14.6÷3.4
(保留两位小数) (保留整数)
≈0.40
≈4
0.40末尾的0能去掉吗?
易错点
求商的近似数时,有时保留指定的小数位数后,近似数的末尾有0,此时的0不能去掉。
(教材第32页“做一做”)
做一做
(教材第36页第3题)
1.2和1.20的计算结果一样吗?
保留一位小数 保留两位小数 保留三位小数
40÷14
26.37÷31
45.5÷38
2.9
2.86
2.857
0.9
0.85
0.851
1.2
1.20
1.197
2. 算一算,填一填。
求商的近似数时,末位的0不能省略,它表示精确度。
是上午铺路的速度快,还是下午铺路的速度快?
上午工作效率:164.9÷3.5 ≈ 47(米/时)
47>46,所以上午铺路的速度快。
3. 一支铺路队正在铺一段公路。上午工作3.5小时,铺了164.9m;下午工作4.5 小时,铺了206.7m。
(教材第36页第2题)
下午工作效率:206÷4.5 ≈ 46(米/时)
工作效率=工作总量÷工作时间
4. 蜘蛛的爬行速度大约是蜗牛的几倍?
求一个数是另一个数的几倍,用除法。
1.9÷0.045 ≈ 42.2
动物名称 爬行的速度
蜗牛 0.045千米/时
陆龟 0.32千米/时
蜘蛛 1.9千米/时
答:蜘蛛的爬行速度大约是蜗牛的42.2倍。
(教材第36页第4题)
(1)蜘蛛的爬行速度大约是
陆龟的几倍?
1.9÷0.32 ≈ 6
(2)陆龟的爬行速度大约是蜗牛的几倍?
0.32÷0.045 ≈ 7
答:陆龟的爬行速度大约是蜗牛的7倍.
答:蜘蛛的爬行速度大
约是陆龟的6倍。
动物名称 爬行的速度
蜗牛 0.045千米/时
陆龟 0.32千米/时
蜘蛛 1.9千米/时
4.
你还能提出其他数学问题并解答吗?
5.在 里填上合适的运算符号。
[教材P36 练习八 第5题]
81 0.5 =40.5
81 1.5 =54
81 0.5 =162
81 1.5 =82.5
×
÷
÷
+
6.一辆汽车行驶22 km用了2.6升汽油,这辆汽车平均每千米耗油多少升?平均每升汽油能使这辆汽车行驶多少千米?(得数保留一位小数)
2.6÷22≈0.1(升)
22÷2.6≈8.5(km)
答:这辆汽车平均每千米耗油0.1升,平均每升汽油能使这辆汽车行驶8.5 km。
2.6÷22≈0.1(升)
7.m÷1.5=n,n是一个两位小数,保留一位小数后是3.0,m最大是多少?最小呢?
n可能是3.04、3.03、3.02、3.01、2.99、2.98、2.97、2.96、2.95。
m最大是3.04×1.5=4.56,最小是2.95×1.5=4.425。
提升练习
8. 小华在计算一道求7个自然数的平均数(按“四舍五入”法保留两位小数)的题目时,将得数最后一位算错了,他的错误答案是21.83,正确答案应是多少?
错误答案是21.83
得数最后一位算错
正确答案在21.80和21.89之间
7个自然数的和在21.80×7和21.89×7 之间
正确答案
21.80×7 =152.60
21.89×7 =153.23
答:正确答案应是21.86。
153÷7 ≈ 21.86
152.60<153<153.23
这节课你有什么收获?
1.在实际应用中,小数除法取商的近似数时有两种情
况:
(1)除不尽;
(2)除得尽,但是商的小数位数比较多, 实际情况却
不用这么多,如价钱、人数、个数等。
2.求商的近似数时,通常要计算到比保留的小数位数
多 一位,再用“四舍五入”法取商的近似数。
小数除法
人教版五年级数学上册
第6课时 商的近似数
3
按“四舍五入”法求出下列各数的近似数。
2.835 9.954 0.5059
保留整数
保留一位小数
保留两位小数
2.8
10.0
0.5
3
10
1
2.84
9.95
0.51
注:根据要求所得的近似数末尾的0不能去掉。
2.计算下面各题,得数保留两位小数。
12.8×1.09
1.7×0.45
≈13.95
≈0.77
1 2.8
1.0 9
×
1 1 5 2
1 2 8
1 3.9 5 2
0.4 5
1.7
×
3 1 5
4 5
0.7 6 5
用什么方法求出积的近似数的?
四舍五入
爸爸给王鹏买了一筒羽毛球,这筒羽毛球19.4元,每个羽毛球大约多少钱?
(教材第32页例6)
一筒是12个。
从题目中你获得了哪些条件?
要求什么问题?
要求每个羽毛球的价钱,可以用总价÷数量。列式为19.4÷12。
总价
数量
单价
6
一筒是12个。
为什么这里用到了大约?
要求每个羽毛球的价钱,可以用总价÷数量。列式为19.4÷12。
爸爸给王鹏买了一筒羽毛球,这筒羽毛球19.4元,每个羽毛球大约多少钱?
6
爸爸给王鹏买了一筒羽毛球,这筒羽毛球19.4元,每个羽毛球大约多少钱?
那怎么求商的近似数呢?
可以先算出19.4÷12的商,然后按“四舍五入” 法取近似数。
一筒是12个。
6
1 9.4
12
1
1 2
7
4
6
7 2
2
0
1
1 2
8
余数又是8,除不尽了,怎么办?
计算价钱,还用往下继续除吗?
.
0
6
7 2
8
19.4÷12≈
1 9.4
12
1
1 2
7
4
6
7 2
2
0
1
1 2
8
也可以保留一位小数,精确到“角”。
在计算价钱时,一般保留两位小数,即精确到“分”,所以除到第三位够了。
.
0
6
7 2
8
19.4÷12≈
19.4÷12≈
1 9.4
12
1
1 2
7
4
6
7 2
2
0
1
1 2
8
.
0
6
7 2
8
6>5,向前一位进1
2
1.62(元)
保留两位小数是……
19.4÷12≈
1 9.4
12
1
1 2
7
4
6
7 2
2
0
1
1 2
8
.
0
6
7 2
8
1.6(元)
1<5,舍去
那保留一位小数除到第二位也行了。
保留一位小数是……
爸爸给王鹏新买了一筒羽毛球。
一筒是12个。
问题延伸
这筒羽毛球19.4 元,每个大约多少钱?
86
要求每个羽毛球的价钱,可以用总价÷数量。列式为19.86÷12。
19.86÷12
1 9. 8 6
12
1
1 2
7
8
6
7 2
6
6
5
6 0
6
.
0
5
6 0
0
能除尽,还用保留近似数吗?
虽然能除尽,但此题计算的是钱数,最多只能保留两位小数。
19.86÷12
1 9. 8 6
12
1
1 2
7
8
6
7 2
6
6
5
6 0
6
.
0
5
6 0
0
保留一位小数是……
5=5,向前一位进1
2
≈1.62(元)
保留两位小数是……
5=5,向前一位进1
7
≈1.7(元)
怎么求商的近似数?保留到哪一位比较合适?
求商的近似数时,计算到比保留的小数位多一位,再将最后一位“四舍五入”。
怎么求商的近似数?保留到哪一位比较合适?
看——需要保留几位小数;
归纳:
除——除到比需要保留的小数位数多一位;
取——将最后一位“四舍五入”取商的近似值。
9.5
2.6
7 8
6.8×0.37 ≈
2.5
(保留一位小数)
9.5÷2.6 ≈
3.8
算一算,比一比,求积和商的近似值时有什么异同?
6.8
0.3 7
4 7 6
2 0 4
2 5 1 6
.
3
.
0
8
1 7
0
1 6 8
2
0
×
(保留一位小数)
6.8×0.37 ≈
2.5
9.5÷2.6 ≈
3.8
算一算,比一比,求积和商的近似值时有什么异同?
相同点:都是按照“四舍五入”法取近似值的。
不同点
求积的近似值必须算出整个积才能取近似值。
求商的近似值时只要计算出比要求保留的小数多一位小数就可以了。
(保留一位小数)
(保留一位小数)
我发现:在计算小数除法需要求商的近似数时,一般除到比需要保留的小数位数多( 一 )位,再按照( 四舍五)法取商的近似数。保留小数位数,需要连续进位时,近似数末尾的0
( 不能 )(填“能”或“不能”)去掉。
一
四舍五入
不能
求商的近似数的方法
4.8÷2.3 (保留一位小数)
.
0
4 8
2.3
2
4 6
2
0
0
1 6
1 8 4
0
0
8
≈2.1
1.计算下面各题。
.
(教材第32页“做一做”)
做一做
1.55÷3.9 14.6÷3.4
(保留两位小数) (保留整数)
≈0.40
≈4
0.40末尾的0能去掉吗?
易错点
求商的近似数时,有时保留指定的小数位数后,近似数的末尾有0,此时的0不能去掉。
(教材第32页“做一做”)
做一做
(教材第36页第3题)
1.2和1.20的计算结果一样吗?
保留一位小数 保留两位小数 保留三位小数
40÷14
26.37÷31
45.5÷38
2.9
2.86
2.857
0.9
0.85
0.851
1.2
1.20
1.197
2. 算一算,填一填。
求商的近似数时,末位的0不能省略,它表示精确度。
是上午铺路的速度快,还是下午铺路的速度快?
上午工作效率:164.9÷3.5 ≈ 47(米/时)
47>46,所以上午铺路的速度快。
3. 一支铺路队正在铺一段公路。上午工作3.5小时,铺了164.9m;下午工作4.5 小时,铺了206.7m。
(教材第36页第2题)
下午工作效率:206÷4.5 ≈ 46(米/时)
工作效率=工作总量÷工作时间
4. 蜘蛛的爬行速度大约是蜗牛的几倍?
求一个数是另一个数的几倍,用除法。
1.9÷0.045 ≈ 42.2
动物名称 爬行的速度
蜗牛 0.045千米/时
陆龟 0.32千米/时
蜘蛛 1.9千米/时
答:蜘蛛的爬行速度大约是蜗牛的42.2倍。
(教材第36页第4题)
(1)蜘蛛的爬行速度大约是
陆龟的几倍?
1.9÷0.32 ≈ 6
(2)陆龟的爬行速度大约是蜗牛的几倍?
0.32÷0.045 ≈ 7
答:陆龟的爬行速度大约是蜗牛的7倍.
答:蜘蛛的爬行速度大
约是陆龟的6倍。
动物名称 爬行的速度
蜗牛 0.045千米/时
陆龟 0.32千米/时
蜘蛛 1.9千米/时
4.
你还能提出其他数学问题并解答吗?
5.在 里填上合适的运算符号。
[教材P36 练习八 第5题]
81 0.5 =40.5
81 1.5 =54
81 0.5 =162
81 1.5 =82.5
×
÷
÷
+
6.一辆汽车行驶22 km用了2.6升汽油,这辆汽车平均每千米耗油多少升?平均每升汽油能使这辆汽车行驶多少千米?(得数保留一位小数)
2.6÷22≈0.1(升)
22÷2.6≈8.5(km)
答:这辆汽车平均每千米耗油0.1升,平均每升汽油能使这辆汽车行驶8.5 km。
2.6÷22≈0.1(升)
7.m÷1.5=n,n是一个两位小数,保留一位小数后是3.0,m最大是多少?最小呢?
n可能是3.04、3.03、3.02、3.01、2.99、2.98、2.97、2.96、2.95。
m最大是3.04×1.5=4.56,最小是2.95×1.5=4.425。
提升练习
8. 小华在计算一道求7个自然数的平均数(按“四舍五入”法保留两位小数)的题目时,将得数最后一位算错了,他的错误答案是21.83,正确答案应是多少?
错误答案是21.83
得数最后一位算错
正确答案在21.80和21.89之间
7个自然数的和在21.80×7和21.89×7 之间
正确答案
21.80×7 =152.60
21.89×7 =153.23
答:正确答案应是21.86。
153÷7 ≈ 21.86
152.60<153<153.23
这节课你有什么收获?
1.在实际应用中,小数除法取商的近似数时有两种情
况:
(1)除不尽;
(2)除得尽,但是商的小数位数比较多, 实际情况却
不用这么多,如价钱、人数、个数等。
2.求商的近似数时,通常要计算到比保留的小数位数
多 一位,再用“四舍五入”法取商的近似数。
