五年级数学上册 最新人教版第六单元第7课时 组合图形的面积课件(共30张PPT)
文档属性
| 名称 | 五年级数学上册 最新人教版第六单元第7课时 组合图形的面积课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 14:49:19 | ||
图片预览






文档简介
(共30张PPT)
多边形的面积
6
人教版五年级数学上册
第7课时 组合图形的面积
正方形面积 =边长×边长
三角形面积 =底×高÷2
平行四边形面积 = 底×高
梯形面积 =( 上底+下底)×高÷2
S =ah
S =ab
S =ah÷2
S =a2
S=(a+b)h÷2
a
长方形面积 = 长×宽
b
a
a
a
h
a
h
h
a
b
在实际生活中,有些图形是由几个简单的图形组合而成的。
这些组合图形里有哪些学过的图形?
2个梯形
1个长方形
2个三角形
1个梯形
1个三角形
1个三角形和1个长方形
……
窗户由4个小小正方形组成
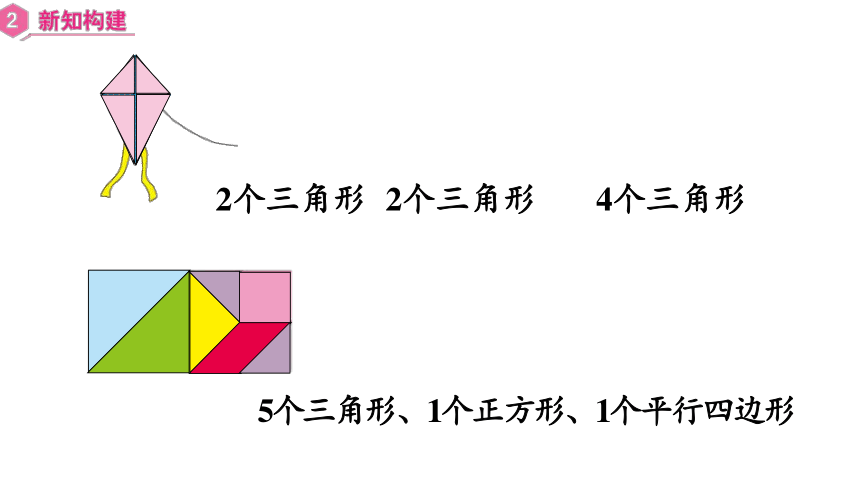
2个三角形
2个三角形
4个三角形
5个三角形、1个正方形、1个平行四边形
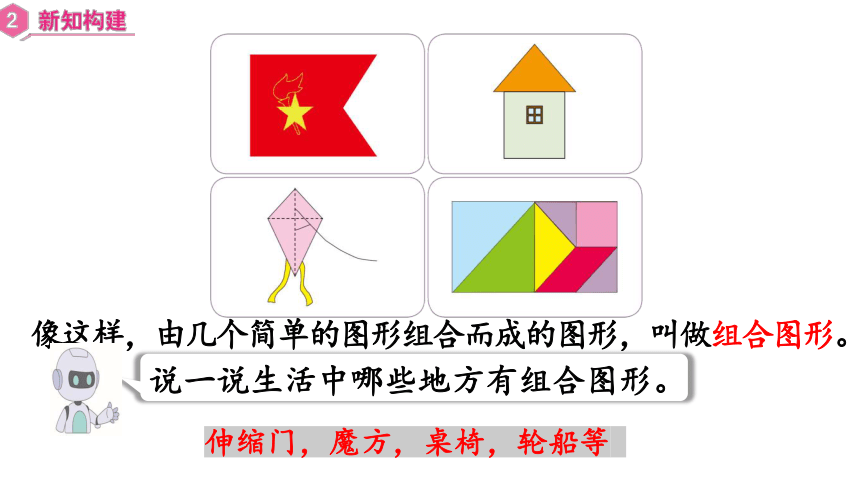
像这样,由几个简单的图形组合而成的图形,叫做组合图形。
说一说生活中哪些地方有组合图形。
伸缩门,魔方,桌椅,轮船等
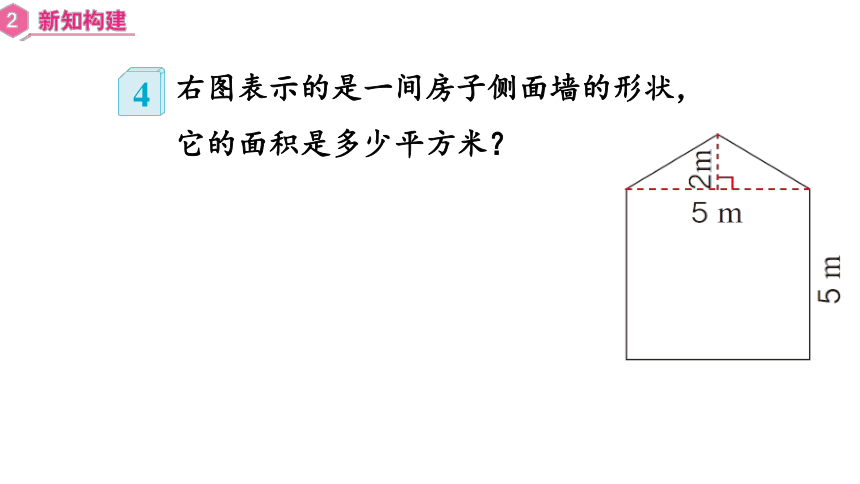
右图表示的是一间房子侧面墙的形状,
它的面积是多少平方米?
4
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
房子侧面墙是一个组合图形,无法直接利用公式求面积,怎么办呢?
可以采用“割”或“补”的方法,把它转化成已学过的几个简单图形来求它的面积。
教材第99页例4
4
小组合作:在图上画出你们的思路,再求出面积,看哪一组的方法最多。
合作要求
1.先各自尝试解题:画出思路,求出面积。
2.组内交流,说说自己的做法。
3.汇总小结,准备全班汇报。
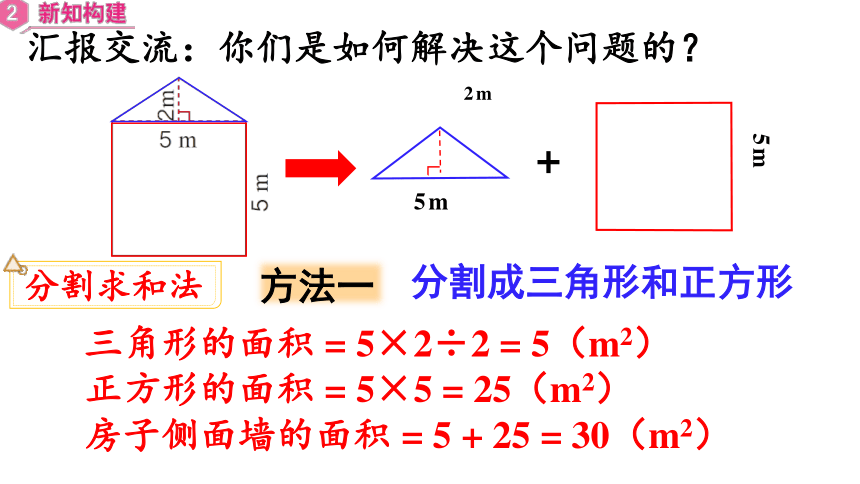
汇报交流:你们是如何解决这个问题的?
三角形的面积 = 5×2÷2 = 5(m2)
正方形的面积 = 5×5 = 25(m2)
房子侧面墙的面积 = 5 + 25 = 30(m2)
方法一
分割成三角形和正方形
+
分割求和法
5m
2m
5m
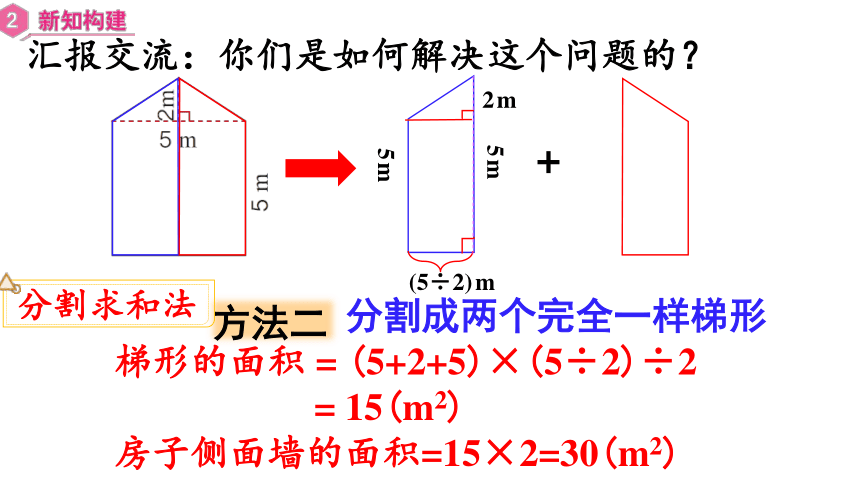
梯形的面积 = (5+2+5)×(5÷2)÷2
= 15(m2)
房子侧面墙的面积=15×2=30(m2)
方法二
分割成两个完全一样梯形
+
汇报交流:你们是如何解决这个问题的?
分割求和法
5m
2m
5m
(5÷2)m
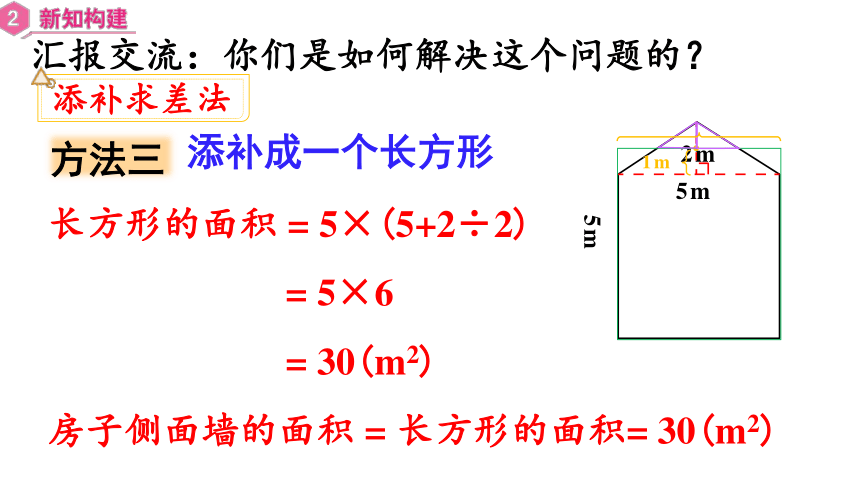
长方形的面积 = 5×(5+2÷2)
= 5×6
= 30(m2)
房子侧面墙的面积 = 长方形的面积= 30(m2)
方法三
添补成一个长方形
汇报交流:你们是如何解决这个问题的?
添补求差法
5m
2m
1m
5m
长方形的面积 =(5+2)×5
= 35(m2)
两个三角形的面积 = 2×(5÷2)÷2×2
= 5(m2)
房子侧面墙的面积 = 35 - 5 = 30(m2)
2.5m
2m
方法四
从长方形中挖去两个小三角形
汇报交流:你们是如何解决这个问题的?
添补求差法
解决组合图形的面积可以采取两种方法,就是分割求和法和添补求差法。
方法一
方法二
方法三
方法四
组合图形面积的计算方法
1.根据已知条件对组合图形进行分割(添补),把组合图形转化成已学过的几个简单图形;
2.分别计算出简单图形的面积;
3.对这些简单图形的面积求和或求差。
仔细观察这几种解题的方法,你发现了什么?
1.填一填。
(1)
要求左面图形的面积,可以把它分割成( )形和( ) 形,也可以把它分割成( ) 形和( )形。
长方
三角
梯
梯
(2)
平行四边形
梯形
2.新丰小学有一块菜地,形状如右图。这块菜地的面积是多少平方米?
50×33 = 1650(m2)
1650+210 =1860(m2)
答:
这块菜地的面积是1860 m2。
35×12÷2 = 210(m2)
教材第99页第1题
3.一面中国少年先锋队中队旗的面积是多少?
80 cm
20 cm
30 cm
30 cm
你能想出几种算法?
教材第99页第2题
80 cm
20 cm
30 cm
30 cm
梯 形:(80-20+80)×30÷2 = 2100(cm2)
中队旗:2100×2 = 4200(cm2)
答:中队旗的面积是4200 cm2。
方法一
分割成两个完全一样的梯形
教材第99页第2题
80 cm
20 cm
30 cm
30 cm
长方形:(80-20)×(30+30)= 3600(cm2)
三角形:30×20÷2 = 300(cm )
中队旗:3600+300×2 = 4200(cm2)
答:中队旗的面积是4200 cm2 。
方法二
分割成一个长方形和两个小三角形
80 cm
20 cm
30 cm
30 cm
长方形:80×(30+30)= 4800(cm2)
三角形:(30+30)×20÷2 = 600(cm )
中队旗:4800-600 = 4200(cm2)
答:中队旗的面积是4200 cm2 。
方法三
看作一个大长方形剪去一个三角形
4.右面是一块正方形空心地砖,它实际占地面积是多少?
30×30 - 13×13 = 731(cm2)
答:它实际占地的面积是 731 cm2。
教材第99页第3题
可看作从一个大正方形里挖去一个小正方形
5.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
梯 形:(40+70)×30÷2 = 1650(m2)
长方形: 30×15 = 450(m2)
草 地: 1650-450 = 1200(m2)
答:草地的面积是1200 m2。
教材第99页第4题
这里可看成一个大梯形挖去一个小长方形
6.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
教材第99页第5题
可看成一个大梯形挖去一个三角形和一个小梯形
大梯形:(2+10)×12÷2 = 72(cm )
三角形:3×4÷2 = 6(cm )
小梯形:(4+6)×4÷2 = 20(cm )
字母“A”:72-6-20 = 46(cm )
答:它的面积是46 cm 。
6.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
可看成一个大梯形挖去一个三角形和一个小梯形
教材第101页第5题
10cm
10cm
20 cm
20cm
7.一个指示牌的形状是一个组合图形,求它的面积。
长方形:20×10 = 200(cm2)
三角形: 20×10÷2 =100(cm2)
指示牌:200+100 = 300(cm2)
答:它的面积是300 cm2。
可分成一个长方形和一个三角形
教材第99页第6题
8.(易错题)计算下面图形的面积。
正解:7×5+7×2÷2=42(cm )
错因分析:组合图形分成了一个三角形和一个平行四边形,其中三角形的底应该是7 cm,而不是5 cm。
反思:将组合图形分成几个简单图形,在计算每个简单图形的面积时要找准数据。
9.求图中阴影部分的面积。(单位:cm)
6
6
3
3
思路一
阴影部分面积=大正方形面积+小正方形面积-空白三角形面积-空白梯形面积
大正方形:6×6 = 36(cm2)
小正方形:3×3 = 9(cm2)
空白三角形:3×3÷2 = 4.5(cm2)
空白梯形: (6-3+6)×6÷2 = 27(cm2)
阴影部分:36+9-4.5-27 = 13.5(cm2)
答:阴影部分的面积是13.5 cm2。
思路二
只看阴影部分,把它分成两个小三角形
阴影小三角形:3×3÷2 = 4.5(cm2)
阴影大三角形:6×3÷2 = 9(cm2)
阴影部分:4.5 + 9 = 13.5(cm2)
答:阴影部分的面积是13.5 cm2 。
9.求图中阴影部分的面积。(单位:cm)
6
6
3
3
思路三
把阴影部分看作一个梯形
梯形:(3+6)×3÷2 =13.5(cm2)
答:阴影部分的面积是13.5 cm2 。
9.图中阴影部分的面积。(单位:cm)
6
6
3
3
1.组合图形:由几个简单的图形组合而成的图形。
2. 组合图形面积的计算方法
(1)借助辅助线将它们分解;
(2)分别计算每个图形的面积;
(3)根据这些图形的组合特点求和或求差。
3.在解答过程中,如果有多种解法,要善于多中选优,选择最简便的方法。
这节课你有什么收获?
多边形的面积
6
人教版五年级数学上册
第7课时 组合图形的面积
正方形面积 =边长×边长
三角形面积 =底×高÷2
平行四边形面积 = 底×高
梯形面积 =( 上底+下底)×高÷2
S =ah
S =ab
S =ah÷2
S =a2
S=(a+b)h÷2
a
长方形面积 = 长×宽
b
a
a
a
h
a
h
h
a
b
在实际生活中,有些图形是由几个简单的图形组合而成的。
这些组合图形里有哪些学过的图形?
2个梯形
1个长方形
2个三角形
1个梯形
1个三角形
1个三角形和1个长方形
……
窗户由4个小小正方形组成
2个三角形
2个三角形
4个三角形
5个三角形、1个正方形、1个平行四边形
像这样,由几个简单的图形组合而成的图形,叫做组合图形。
说一说生活中哪些地方有组合图形。
伸缩门,魔方,桌椅,轮船等
右图表示的是一间房子侧面墙的形状,
它的面积是多少平方米?
4
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
房子侧面墙是一个组合图形,无法直接利用公式求面积,怎么办呢?
可以采用“割”或“补”的方法,把它转化成已学过的几个简单图形来求它的面积。
教材第99页例4
4
小组合作:在图上画出你们的思路,再求出面积,看哪一组的方法最多。
合作要求
1.先各自尝试解题:画出思路,求出面积。
2.组内交流,说说自己的做法。
3.汇总小结,准备全班汇报。
汇报交流:你们是如何解决这个问题的?
三角形的面积 = 5×2÷2 = 5(m2)
正方形的面积 = 5×5 = 25(m2)
房子侧面墙的面积 = 5 + 25 = 30(m2)
方法一
分割成三角形和正方形
+
分割求和法
5m
2m
5m
梯形的面积 = (5+2+5)×(5÷2)÷2
= 15(m2)
房子侧面墙的面积=15×2=30(m2)
方法二
分割成两个完全一样梯形
+
汇报交流:你们是如何解决这个问题的?
分割求和法
5m
2m
5m
(5÷2)m
长方形的面积 = 5×(5+2÷2)
= 5×6
= 30(m2)
房子侧面墙的面积 = 长方形的面积= 30(m2)
方法三
添补成一个长方形
汇报交流:你们是如何解决这个问题的?
添补求差法
5m
2m
1m
5m
长方形的面积 =(5+2)×5
= 35(m2)
两个三角形的面积 = 2×(5÷2)÷2×2
= 5(m2)
房子侧面墙的面积 = 35 - 5 = 30(m2)
2.5m
2m
方法四
从长方形中挖去两个小三角形
汇报交流:你们是如何解决这个问题的?
添补求差法
解决组合图形的面积可以采取两种方法,就是分割求和法和添补求差法。
方法一
方法二
方法三
方法四
组合图形面积的计算方法
1.根据已知条件对组合图形进行分割(添补),把组合图形转化成已学过的几个简单图形;
2.分别计算出简单图形的面积;
3.对这些简单图形的面积求和或求差。
仔细观察这几种解题的方法,你发现了什么?
1.填一填。
(1)
要求左面图形的面积,可以把它分割成( )形和( ) 形,也可以把它分割成( ) 形和( )形。
长方
三角
梯
梯
(2)
平行四边形
梯形
2.新丰小学有一块菜地,形状如右图。这块菜地的面积是多少平方米?
50×33 = 1650(m2)
1650+210 =1860(m2)
答:
这块菜地的面积是1860 m2。
35×12÷2 = 210(m2)
教材第99页第1题
3.一面中国少年先锋队中队旗的面积是多少?
80 cm
20 cm
30 cm
30 cm
你能想出几种算法?
教材第99页第2题
80 cm
20 cm
30 cm
30 cm
梯 形:(80-20+80)×30÷2 = 2100(cm2)
中队旗:2100×2 = 4200(cm2)
答:中队旗的面积是4200 cm2。
方法一
分割成两个完全一样的梯形
教材第99页第2题
80 cm
20 cm
30 cm
30 cm
长方形:(80-20)×(30+30)= 3600(cm2)
三角形:30×20÷2 = 300(cm )
中队旗:3600+300×2 = 4200(cm2)
答:中队旗的面积是4200 cm2 。
方法二
分割成一个长方形和两个小三角形
80 cm
20 cm
30 cm
30 cm
长方形:80×(30+30)= 4800(cm2)
三角形:(30+30)×20÷2 = 600(cm )
中队旗:4800-600 = 4200(cm2)
答:中队旗的面积是4200 cm2 。
方法三
看作一个大长方形剪去一个三角形
4.右面是一块正方形空心地砖,它实际占地面积是多少?
30×30 - 13×13 = 731(cm2)
答:它实际占地的面积是 731 cm2。
教材第99页第3题
可看作从一个大正方形里挖去一个小正方形
5.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
梯 形:(40+70)×30÷2 = 1650(m2)
长方形: 30×15 = 450(m2)
草 地: 1650-450 = 1200(m2)
答:草地的面积是1200 m2。
教材第99页第4题
这里可看成一个大梯形挖去一个小长方形
6.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
教材第99页第5题
可看成一个大梯形挖去一个三角形和一个小梯形
大梯形:(2+10)×12÷2 = 72(cm )
三角形:3×4÷2 = 6(cm )
小梯形:(4+6)×4÷2 = 20(cm )
字母“A”:72-6-20 = 46(cm )
答:它的面积是46 cm 。
6.小欣用一张红色不干胶纸剪了一个大写英文字母“A”。它的面积是多少?
可看成一个大梯形挖去一个三角形和一个小梯形
教材第101页第5题
10cm
10cm
20 cm
20cm
7.一个指示牌的形状是一个组合图形,求它的面积。
长方形:20×10 = 200(cm2)
三角形: 20×10÷2 =100(cm2)
指示牌:200+100 = 300(cm2)
答:它的面积是300 cm2。
可分成一个长方形和一个三角形
教材第99页第6题
8.(易错题)计算下面图形的面积。
正解:7×5+7×2÷2=42(cm )
错因分析:组合图形分成了一个三角形和一个平行四边形,其中三角形的底应该是7 cm,而不是5 cm。
反思:将组合图形分成几个简单图形,在计算每个简单图形的面积时要找准数据。
9.求图中阴影部分的面积。(单位:cm)
6
6
3
3
思路一
阴影部分面积=大正方形面积+小正方形面积-空白三角形面积-空白梯形面积
大正方形:6×6 = 36(cm2)
小正方形:3×3 = 9(cm2)
空白三角形:3×3÷2 = 4.5(cm2)
空白梯形: (6-3+6)×6÷2 = 27(cm2)
阴影部分:36+9-4.5-27 = 13.5(cm2)
答:阴影部分的面积是13.5 cm2。
思路二
只看阴影部分,把它分成两个小三角形
阴影小三角形:3×3÷2 = 4.5(cm2)
阴影大三角形:6×3÷2 = 9(cm2)
阴影部分:4.5 + 9 = 13.5(cm2)
答:阴影部分的面积是13.5 cm2 。
9.求图中阴影部分的面积。(单位:cm)
6
6
3
3
思路三
把阴影部分看作一个梯形
梯形:(3+6)×3÷2 =13.5(cm2)
答:阴影部分的面积是13.5 cm2 。
9.图中阴影部分的面积。(单位:cm)
6
6
3
3
1.组合图形:由几个简单的图形组合而成的图形。
2. 组合图形面积的计算方法
(1)借助辅助线将它们分解;
(2)分别计算每个图形的面积;
(3)根据这些图形的组合特点求和或求差。
3.在解答过程中,如果有多种解法,要善于多中选优,选择最简便的方法。
这节课你有什么收获?
