8.2一元线性回归模型及其应用 同步练习(含解析)2023——2024学年高中数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 8.2一元线性回归模型及其应用 同步练习(含解析)2023——2024学年高中数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 14:51:11 | ||
图片预览




文档简介
8.2 一元线性回归模型及其应用 同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在研究变量与之间的关系时,进行实验后得到了一组样本数据利用此样本数据求得的经验回归方程为,现发现数据和误差较大,剔除这两对数据后,求得的经验回归方程为,且则( )
A.8 B.12 C.16 D.20
2.为维护市场秩序,保护消费者权益,在“五一”假期来临之际,我市物价部门对某商品在5家商场的售价(元)及其一天的销售量(件)进行调查,得到五对数据,经过分析、计算,得,关于的经验回归方程为,则相应于点的残差为( )
A. B.1 C. D.3
3.已知变量x与y具有线性相关关系,在研究变量x与y之间的关系时,进行实验后得到了一组样本数据,利用此样本数据求得的线性回归方程为,现发现数据和误差较大,剔除这两对数据后,求得的线性回归方程为,且,则( )
A.8 B.12 C.16 D.20
4.色差和色度是衡量毛绒玩具质量优劣的重要指标.现抽检一批毛绒玩具,测得的色差和色度数据如表所示:
色差x 21 23 25 27
色度y m 18 19 20
根据表中数据可得色度关于色差的经验回归方程为,则( )
A.14 B.15 C.16 D.17
5.已知某一家旗舰店近五年“五一”黄金周期间的成交额如下表:
年份 2019 2020 2021 2022 2023
年份代号 1 2 3 4 5
成交额y(万元) 50 60 70 80 100
若关于的线性回归方程为,则根据回归方程预测该店2024年“五一”黄金周的成交额是( )
A.84万元 B.96万元 C.108万元 D.120万元
6.某校地理小组在某座山测得海拔高度、气压和沸点的六组数据绘制成散点图如图,则下列说法不正确的是( )
A.气压与海拔高度呈正相关 B.沸点与气压呈正相关
C.沸点与海拔高度呈负相关 D.沸点与海拔高度、沸点与气压的相关性都很强
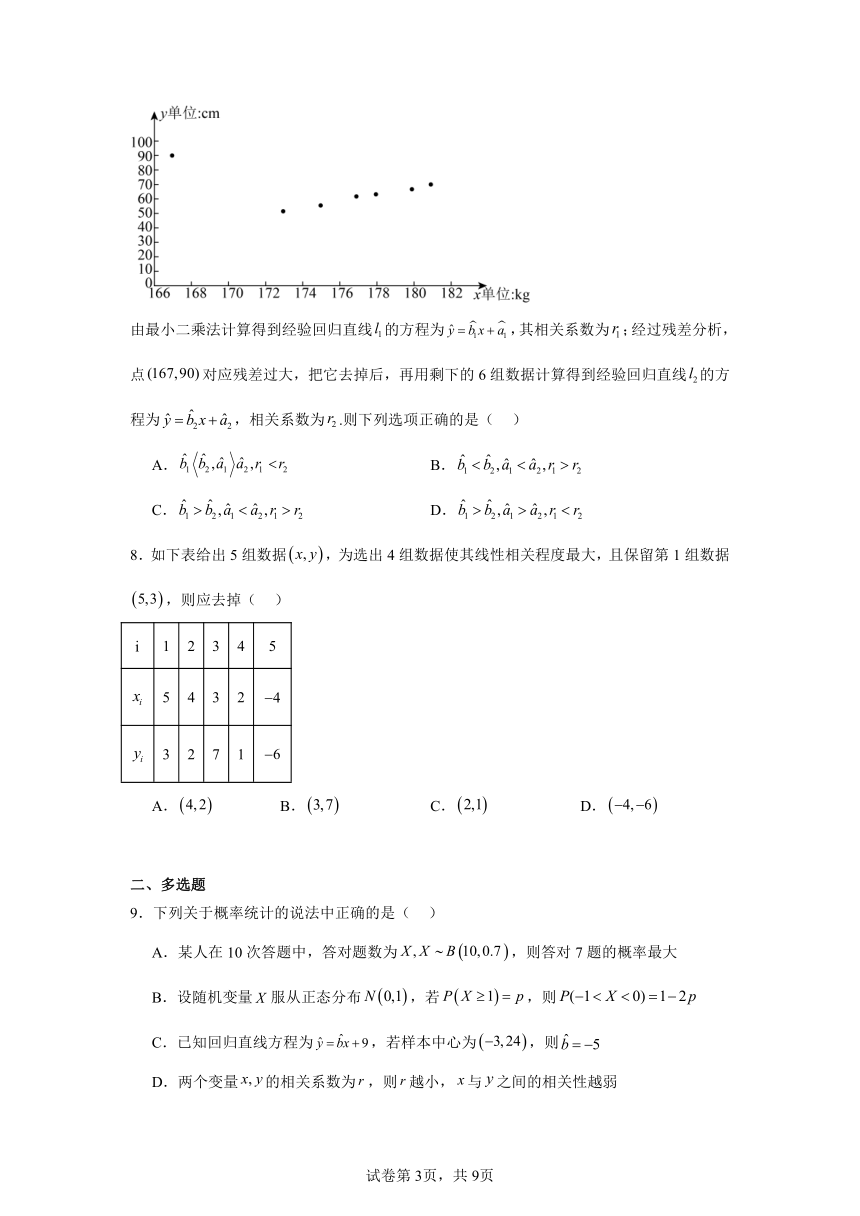
7.某校为了解本校高一男生身高和体重的相关关系,在该校高一年级随机抽取了7名男生,测量了他们的身高和体重得下表:
身高x(单位:) 167 173 175 177 178 180 181
体重y(单位:) 90 54 59 64 67 72 76
由表格制作成如图所示的散点图:
由最小二乘法计算得到经验回归直线的方程为,其相关系数为;经过残差分析,点对应残差过大,把它去掉后,再用剩下的6组数据计算得到经验回归直线的方程为,相关系数为.则下列选项正确的是( )
A. B.
C. D.
8.如下表给出5组数据,为选出4组数据使其线性相关程度最大,且保留第1组数据,则应去掉( )
1 2 3 4 5
5 4 3 2
3 2 7 1
A. B. C. D.
二、多选题
9.下列关于概率统计的说法中正确的是( )
A.某人在10次答题中,答对题数为,则答对7题的概率最大
B.设随机变量服从正态分布,若,则
C.已知回归直线方程为,若样本中心为,则
D.两个变量的相关系数为,则越小,与之间的相关性越弱
10.下列说法中,正确的是( )
A.一组数据10,11,11,12,13,14,16,18,20,22的第40百分位数为12
B.两组样本数据,,,和,,,的方差分别为,,若已知(),则
C.已知随机变量服从正态分布,若,则
D.已知一系列样本点()的回归方程为,若样本点与的残差(残差=实际值-模型预测值)相等,则
11.下列命题正确的是( )
A.已知由一组样本数据,得到的回归直线方程为,且,则这组样本数据中一定有
B.某学校高三年级学生有男生500人,女生400人,为了获得该校高三全体学生的身高信息,现采用样本量比例分配的分层随机抽样方法抽取了容量为180的样本,经计算得男生样本的均值为170,方差为19,女生样本的均值为161,方差为28,则抽取的样本的方差为43
C.已知互不相同的30个样本数据,若去掉其中最大和最小的数据,则剩下28个数据的分位数可能等于原样本数据的分位数
D.若随机变量,且,则
12.相关变量x,y的散点图如下,若剔除点13后,剩下数据得到的统计中,较剔除之前值变小的是( )
A.样本的相关系数 B.残差的平方和
C.样本数据y的平均值 D.回归直线中的回归系数
三、填空题
13.某工厂为研究某种产品的产量x(吨)与所需某种原材料的质量y(吨)的相关性,在生产过程中收集4组对应数据,如表所示.
x 3 4 5 6
y 2.5 3 4 m
根据表中数据,得出y关于x的经验回归方程为,则表中m的值为 .
14.已知,之间的一组数据:
若与满足回归方程,则此曲线必过点 .
15.某公司为了了解某商品的月销售量单位:万件与月销售单价单位:元件之间的关系,随机统计了个月的销售量与销售单价,并制作了如下对照表:
月销售单价元件
月销售量万件
由表中数据可得回归方程中,试预测当月销售单价为元件时,月销售量为 万件.
16.随着夏季的来临,遮阳帽开始畅销,某商家为了解某种遮阳帽如何定价才可以获得最大利润,现对这种遮阳帽进行试销售,经过统计发现销售量(单位:顶)与单价(单位:元)具有线性相关关系,且线性回归方程为,若想要销售量为80顶,则预计该遮阳帽的单价定为 元.
四、解答题
17.某商场推出“云闪付”购物活动,由于推广期内优惠力度较大,吸引了越来越多的顾客使用这种支付方式.现统计了活动刚推出一周内每天使用“云闪付”支付的人数,用表示活动推出的天数,表示每天使用该支付方式的人数,统计数据如下表所示:
1 2 3 4 5 6 7
6 13 25 40 73 110 201
根据散点图判断,在推广期内,支付的人数关于天数的回归方程适合用表示.
(1)求该回归方程,并预测活动推出第8天使用“云闪付”的人数;(的结果精确到0.01)
(2)推广期结束后,商场对顾客的支付方式进行统计,结果如下表:
支付方式 云闪付 会员卡 其它支付方式
比例
商场规定:使用会员卡支付的顾客享8折,“云闪付”的顾客随机优惠,其它支付方式的顾客无优惠,根据统计结果得知,使用“云闪付”的顾客,享7折的概率为,享8折的概率为,享9折的概率为.设顾客购买标价为元的商品支付的费用为,根据所给数据用事件发生的频率估计相应事件发生的概率,写出的分布列,并求.
参考数据:设.
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计公式分别为:.
18.某公司为考核员工,采用某方案对员工进行业务技能测试,并统计分析测试成绩以确定员工绩效等级.
(1)已知该公司甲部门有3名负责人,乙部门有4名负责人,该公司从甲、乙两部门中随机选取3名负责人做测试分析,记负责人来自甲部门的人数为,求的最有可能的取值:
(2)该公司统计了七个部门测试的平均成绩(满分100分)与绩效等级优秀率,如下表所示:
32 41 54 68 74 80 92
0.28 0.34 0.44 0.58 0.66 0.74 0.94
根据数据绘制散点图,初步判断,选用作为回归方程.令,经计算得,
(ⅰ)已知某部门测试的平均成绩为60分,估计其绩效等级优秀率;
(ⅱ)根据统计分析,大致认为各部门测试平均成绩,其中近似为样本平均数,近似为样本方差.经计算,求某个部门绩效等级优秀率不低于的概率.
参考公式与数据:①.
②线性回归方程中,,.
③若随机变量,则,,.
19.某公司为提升款产品的核心竞争力,准备加大款产品的研发投资,为确定投入款产品的年研发费用,需了解年研发费用(单位:万元)对年利润(单位:万元)的影响.该公司统计了最近8年每年投入款产品的年研发费用与年利润的数据,得到下图所示的散点图:
经数据分析知,与正线性相关,且相关程度较高.经计算得,.
(1)建立关于的经验回归方程;
(2)若该公司对款产品欲投入的年研发费用为30万元,根据(1)得到的经验回归方程,预测年利润为多少万元
附:.
20.某地5家超市春节期间的广告支出x(万元)与销售额y(万元)的数据如下:
超市 A B C D E
广告支出x 2 4 5 6 8
销售额y 30 40 60 60 70
(1)从A,B,C,D,E这5家超市中随机抽取3家,记销售额不少于60万元的超市个数为X,求随机变量X的分布列及期望;
(2)利用最小二乘法求y关于x的线性回归方程,并预测广告支出为10万元时的销售额.
附:线性回归方程中斜率和截距的最小二乘估计公式分别为:,.
21.某市2017年至2023年城镇居民人均可支配收入如下表,将其绘制成散点图(如下图),发现城镇居民人均可支配收入y(单位:万元)与年份代号x具有线性相关关系.
年份 2017 2018 2019 2020 2021 2022 2023
年份代号 1 2 3 4 5 6 7
人均可支配收入 3.65 3.89 4.08 4.30 4.65 4.90 5.12
(1)求y关于x的线性回归方程,并根据所求回归方程,预测2024年该市城镇居民人均可支配收入;
(2)某分析员从2017年至2023年人均可支配收入中,任取3年的数据进行分析,记其中人均可支配收入超过4.5万的年份个数为随机变量X,求X的分布列与数学期望.
参考数据及公式:,,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】由题意,求出剔除后的平均数,进而求出剔除前的平均数,根据回归直线必过样本点中心得到,进而得到,将点代入,即可求解.
【详解】设没剔除两对数据前的平均数分别为,,
剔除两对数据后的平均数分别为,,
因为,
所以,,
则,
所以,
又因为,
所以,
解得.
故选:C.
2.A
【分析】将样本点中心,并代入回归方程,求,并代入后,即可求解残差.
【详解】因为回归直线过样本点中心即,代入,可得,
解得,当时,,所以残差为.
故选:A
3.C
【分析】由题意求出剔除后的平均数,进而求出剔除前的平均数,根据回归直线必过样本点中心,得到,进而得到,将点代入,即可求解.
【详解】设没剔除两对数据前的,的平均数分别为,,
剔除两对数据后的,的平均数分别为,,
因为,所以,则,
因为两对数据为和,所以,
所以,
所以,解得.
故选:C.
4.B
【分析】首先由表示出样本中心点,再代入经验回归方程,计算可得.
【详解】由题可得,
,
因为经验回归直线必过样本中心点,
所以,解得.
故选:B.
5.C
【分析】根据样本中心求解,即可代入求解.
【详解】由表中数据可得,
将代入可得,
故,当时,所以万元,
故选:C
6.A
【分析】利用散点图的规律分析气压与高度、沸点与气压、沸点与海拔高度的相关性即可判定.
【详解】由图1知气压随海拔高度的增加而减小,由图2知沸点随气压的升高而升高,
所以气压与海拔高度呈负相关,沸点与气压呈正相关,沸点与海拔高度呈负相关.
由于两个散点图中的点都呈线性分布,
所以沸点与海拔高度、沸点与气压的相关性都很强,故B,C,D正确,A错误.
故选:A.
7.A
【分析】根据的特点判断斜率和截距;由于去掉,其它点的线性关系更强,从而可判断相关系数.
【详解】身高的平均数为,
因为离群点的横坐标167小于平均值176,纵坐标90相对过大,
所以去掉后经验回归直线的截距变小而斜率变大,故,
去掉后相关性更强,拟合效果也更好,且还是正相关,所以.
故选:A
8.B
【分析】画出散点图,根据线性相关性与偏离程度判断即可.
【详解】根据表格数据,得到散点图如下所示:
由散点图可知数据偏离程度最高,故应该去掉数据.
故选:B
9.AC
【分析】对于A,可利用不等式法求解;对于B,根据正态分布曲线的对称性即可验算;对于C,将样本中心坐标代入回归方程即可验算;对于D,由相关系数的意义即可判断.
【详解】对于,故,
令,解得,故,故A正确;
对于,故错误;
对于,回归直线必过样本中心,可得,解得,故C正确;
对于,两个变量的相关系数为越小,与之间的相关性越弱,故D错误.
故选:AC.
10.BC
【分析】A选项,根据百分位数的运算公式得到答案;B选项,利用平均数定义得到,根据方差的计算公式得到;C选项,由正态分布的对称性得到C正确;D选项,由题意得到,得到D错误.
【详解】A选项,,故从小到大从第4个和第5个数的平均数作为第40百分位数,即,A错误;
B选项,,,
因为,(),故,
故,
,
故,B正确;
C选项,因为,,
关于对称,所以,C正确;
D选项,由题意得,整理得,D错误.
故选:BC
11.BD
【分析】根据题意,结合回归方程的性质,样本均值和方程的计算方法,以及百分位数的计算方法,正态分布的概率计算,逐项判定,即可求解.
【详解】对于A中,根据回归方程经过样本中心,但样本中心不一定是数据中的点,
所以这组数据不一定有,所以A错误;
对于中,样本均值,
样本方差:
,所以B正确
对于C中,将这原来的30个数从小到大排列为,则,
所以原来的分位数为,
若去掉其中最大和最小的数据,剩下28个数据为,则,
以剩下28个数据的分位数为,由于互不相同,所以C不正确;
对于D中,由,
则,所以D正确.
故选:BD.
12.ABC
【分析】根据已知条件,结合变量间的相关关系,结合图象分析判断即可.
【详解】由散点图可知,去掉点后,与的线性相关加强,且为负相关,
所以样本的相关系数变小,残差的平方和变小,样本数据y的平均值变小,故ABC正确;
回归直线中的回归系数变大,故D错误.
故选:ABC.
13.4.5
【分析】表示出样本中心点的横、纵坐标,将其代入回归直线方程即可求解.
【详解】样本中心点的横坐标为,样本中心点的纵坐标为,
所以由样本中心点必在回归方程所对应的直线上,可得,解得.
故答案为:4.5.
14.
【分析】令,只需要求和即可得答案.
【详解】解:令,则,,
则必经过点.
故答案为:.
15.
【分析】根据给定数表求出样本中心点,再代入回归直线求出参数即可求得结果.
【详解】依题意,,,
所以样本中心点坐标为,代入回归方程得,,
解得,
所以回归方程为,
当时,,
即当月销售单价为元件时,月销售量约为万件.
故答案为:
16.40
【分析】线性回归方程中,当,求的值.
【详解】若销售量为80顶,则,解得,所以预计单价应定为40元.
故答案为:40
17.(1),355人;
(2)分布列见解析,.
【分析】(1)由两边取常用对数,利用换元法转化为线性归回直线方程并结合公式进行求解;
(2)根据概率的乘法公式进行求解列出分布列,根据期望公式计算结果.
【详解】(1)由,得,设,,,则.
,
.
把样本中心点代入方程得,
所以,即,
其回归方程为,
当时,.
(2)的可能取值为:.
分布列如下:
0.1 0.35 0.15 0.4
所以,购物的平均费用为:.
18.(1)
(2)(ⅰ)(ⅱ)
【分析】(1)依题意的可能取值为,,,,求出所对应的概率,即可判断;
(2)(ⅰ)对两边取对数,由参考数据可知,根据样本中心点求出,即可求出回归方程,再将代入计算可得;(ⅱ)依题意可得,,再令,求出的取值范围,再由正态分布的性质计算可得.
【详解】(1)依题意,随机变量服从超几何分布,且的可能取值为,,,,
则,,,.
由此可得最大,即的可能性最大,故最有可能的取值为;
(2)(ⅰ)依题意,两边取对数,得,
即,其中,
由提供的参考数据,可知,又,故,
所以,
由提供的参考数据,可得,故,
当时,,即估计其绩效等级优秀率为;
(ⅱ)由(ⅰ)及提供的参考数据可知,,,
又,即,可得,即.
又,且,
由正态分布的性质,得,
记“绩效等级优秀率不低于”为事件,则,
所以绩效等级优秀率不低于的概率等于.
19.(1)
(2)65万元
【分析】(1)根据所给数据求出,然后由求得可得回归方程;
(2)将代入回归方程即可得预测值.
【详解】(1),
.
.
关于的经验回归方程为.
(2)由(1)可得,.
当时,.
对款产品投入30万元年研发费用,年利润约为65万元.
20.(1)X的分布列见解析,期望
(2);预测广告费支出10万元时的销售额为87万元.
【分析】(1)根据超几何分布的概率公式求解分布列,进而可求解期望,
(2)利用最小二乘法求解线性回归方程即可.
【详解】(1)从A,B,C,D,E这5家超市中随机抽取3家,记销售额不少于60万元的超市有C,D,E这3家超市,
则随机变量的可能取值为1,2,3
,,,
的分布列为:
1 2 3
数学期望.
(2),,
,
.
关于的线性回归方程为;
在中,取,得.
预测广告费支出10万元时的销售额为87万元.
21.(1),5.37 万元
(2)分布列见解析,期望为.
【分析】(1)求出相关数据,代入公式得到回归直线方程,并代入即可;
(2)首先得到 的可能取值为 0,1,2,3,分步列出分布列,计算期望即可.
【详解】(1)由题意得,,
,
,
,
故,
,
故回归方程为,
又因为2024年的年份编号为8,将代入,解得,
预测2024年该市城镇居民人均可支配收入为5.37万元;
(2)由图表知,人均可支配收入超过4.5万的年份有3年,
故的可能取值为0,1,2,3,则,
,
,
,
故随机变量的分布列为:
0 1 2 3
故.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在研究变量与之间的关系时,进行实验后得到了一组样本数据利用此样本数据求得的经验回归方程为,现发现数据和误差较大,剔除这两对数据后,求得的经验回归方程为,且则( )
A.8 B.12 C.16 D.20
2.为维护市场秩序,保护消费者权益,在“五一”假期来临之际,我市物价部门对某商品在5家商场的售价(元)及其一天的销售量(件)进行调查,得到五对数据,经过分析、计算,得,关于的经验回归方程为,则相应于点的残差为( )
A. B.1 C. D.3
3.已知变量x与y具有线性相关关系,在研究变量x与y之间的关系时,进行实验后得到了一组样本数据,利用此样本数据求得的线性回归方程为,现发现数据和误差较大,剔除这两对数据后,求得的线性回归方程为,且,则( )
A.8 B.12 C.16 D.20
4.色差和色度是衡量毛绒玩具质量优劣的重要指标.现抽检一批毛绒玩具,测得的色差和色度数据如表所示:
色差x 21 23 25 27
色度y m 18 19 20
根据表中数据可得色度关于色差的经验回归方程为,则( )
A.14 B.15 C.16 D.17
5.已知某一家旗舰店近五年“五一”黄金周期间的成交额如下表:
年份 2019 2020 2021 2022 2023
年份代号 1 2 3 4 5
成交额y(万元) 50 60 70 80 100
若关于的线性回归方程为,则根据回归方程预测该店2024年“五一”黄金周的成交额是( )
A.84万元 B.96万元 C.108万元 D.120万元
6.某校地理小组在某座山测得海拔高度、气压和沸点的六组数据绘制成散点图如图,则下列说法不正确的是( )
A.气压与海拔高度呈正相关 B.沸点与气压呈正相关
C.沸点与海拔高度呈负相关 D.沸点与海拔高度、沸点与气压的相关性都很强
7.某校为了解本校高一男生身高和体重的相关关系,在该校高一年级随机抽取了7名男生,测量了他们的身高和体重得下表:
身高x(单位:) 167 173 175 177 178 180 181
体重y(单位:) 90 54 59 64 67 72 76
由表格制作成如图所示的散点图:
由最小二乘法计算得到经验回归直线的方程为,其相关系数为;经过残差分析,点对应残差过大,把它去掉后,再用剩下的6组数据计算得到经验回归直线的方程为,相关系数为.则下列选项正确的是( )
A. B.
C. D.
8.如下表给出5组数据,为选出4组数据使其线性相关程度最大,且保留第1组数据,则应去掉( )
1 2 3 4 5
5 4 3 2
3 2 7 1
A. B. C. D.
二、多选题
9.下列关于概率统计的说法中正确的是( )
A.某人在10次答题中,答对题数为,则答对7题的概率最大
B.设随机变量服从正态分布,若,则
C.已知回归直线方程为,若样本中心为,则
D.两个变量的相关系数为,则越小,与之间的相关性越弱
10.下列说法中,正确的是( )
A.一组数据10,11,11,12,13,14,16,18,20,22的第40百分位数为12
B.两组样本数据,,,和,,,的方差分别为,,若已知(),则
C.已知随机变量服从正态分布,若,则
D.已知一系列样本点()的回归方程为,若样本点与的残差(残差=实际值-模型预测值)相等,则
11.下列命题正确的是( )
A.已知由一组样本数据,得到的回归直线方程为,且,则这组样本数据中一定有
B.某学校高三年级学生有男生500人,女生400人,为了获得该校高三全体学生的身高信息,现采用样本量比例分配的分层随机抽样方法抽取了容量为180的样本,经计算得男生样本的均值为170,方差为19,女生样本的均值为161,方差为28,则抽取的样本的方差为43
C.已知互不相同的30个样本数据,若去掉其中最大和最小的数据,则剩下28个数据的分位数可能等于原样本数据的分位数
D.若随机变量,且,则
12.相关变量x,y的散点图如下,若剔除点13后,剩下数据得到的统计中,较剔除之前值变小的是( )
A.样本的相关系数 B.残差的平方和
C.样本数据y的平均值 D.回归直线中的回归系数
三、填空题
13.某工厂为研究某种产品的产量x(吨)与所需某种原材料的质量y(吨)的相关性,在生产过程中收集4组对应数据,如表所示.
x 3 4 5 6
y 2.5 3 4 m
根据表中数据,得出y关于x的经验回归方程为,则表中m的值为 .
14.已知,之间的一组数据:
若与满足回归方程,则此曲线必过点 .
15.某公司为了了解某商品的月销售量单位:万件与月销售单价单位:元件之间的关系,随机统计了个月的销售量与销售单价,并制作了如下对照表:
月销售单价元件
月销售量万件
由表中数据可得回归方程中,试预测当月销售单价为元件时,月销售量为 万件.
16.随着夏季的来临,遮阳帽开始畅销,某商家为了解某种遮阳帽如何定价才可以获得最大利润,现对这种遮阳帽进行试销售,经过统计发现销售量(单位:顶)与单价(单位:元)具有线性相关关系,且线性回归方程为,若想要销售量为80顶,则预计该遮阳帽的单价定为 元.
四、解答题
17.某商场推出“云闪付”购物活动,由于推广期内优惠力度较大,吸引了越来越多的顾客使用这种支付方式.现统计了活动刚推出一周内每天使用“云闪付”支付的人数,用表示活动推出的天数,表示每天使用该支付方式的人数,统计数据如下表所示:
1 2 3 4 5 6 7
6 13 25 40 73 110 201
根据散点图判断,在推广期内,支付的人数关于天数的回归方程适合用表示.
(1)求该回归方程,并预测活动推出第8天使用“云闪付”的人数;(的结果精确到0.01)
(2)推广期结束后,商场对顾客的支付方式进行统计,结果如下表:
支付方式 云闪付 会员卡 其它支付方式
比例
商场规定:使用会员卡支付的顾客享8折,“云闪付”的顾客随机优惠,其它支付方式的顾客无优惠,根据统计结果得知,使用“云闪付”的顾客,享7折的概率为,享8折的概率为,享9折的概率为.设顾客购买标价为元的商品支付的费用为,根据所给数据用事件发生的频率估计相应事件发生的概率,写出的分布列,并求.
参考数据:设.
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计公式分别为:.
18.某公司为考核员工,采用某方案对员工进行业务技能测试,并统计分析测试成绩以确定员工绩效等级.
(1)已知该公司甲部门有3名负责人,乙部门有4名负责人,该公司从甲、乙两部门中随机选取3名负责人做测试分析,记负责人来自甲部门的人数为,求的最有可能的取值:
(2)该公司统计了七个部门测试的平均成绩(满分100分)与绩效等级优秀率,如下表所示:
32 41 54 68 74 80 92
0.28 0.34 0.44 0.58 0.66 0.74 0.94
根据数据绘制散点图,初步判断,选用作为回归方程.令,经计算得,
(ⅰ)已知某部门测试的平均成绩为60分,估计其绩效等级优秀率;
(ⅱ)根据统计分析,大致认为各部门测试平均成绩,其中近似为样本平均数,近似为样本方差.经计算,求某个部门绩效等级优秀率不低于的概率.
参考公式与数据:①.
②线性回归方程中,,.
③若随机变量,则,,.
19.某公司为提升款产品的核心竞争力,准备加大款产品的研发投资,为确定投入款产品的年研发费用,需了解年研发费用(单位:万元)对年利润(单位:万元)的影响.该公司统计了最近8年每年投入款产品的年研发费用与年利润的数据,得到下图所示的散点图:
经数据分析知,与正线性相关,且相关程度较高.经计算得,.
(1)建立关于的经验回归方程;
(2)若该公司对款产品欲投入的年研发费用为30万元,根据(1)得到的经验回归方程,预测年利润为多少万元
附:.
20.某地5家超市春节期间的广告支出x(万元)与销售额y(万元)的数据如下:
超市 A B C D E
广告支出x 2 4 5 6 8
销售额y 30 40 60 60 70
(1)从A,B,C,D,E这5家超市中随机抽取3家,记销售额不少于60万元的超市个数为X,求随机变量X的分布列及期望;
(2)利用最小二乘法求y关于x的线性回归方程,并预测广告支出为10万元时的销售额.
附:线性回归方程中斜率和截距的最小二乘估计公式分别为:,.
21.某市2017年至2023年城镇居民人均可支配收入如下表,将其绘制成散点图(如下图),发现城镇居民人均可支配收入y(单位:万元)与年份代号x具有线性相关关系.
年份 2017 2018 2019 2020 2021 2022 2023
年份代号 1 2 3 4 5 6 7
人均可支配收入 3.65 3.89 4.08 4.30 4.65 4.90 5.12
(1)求y关于x的线性回归方程,并根据所求回归方程,预测2024年该市城镇居民人均可支配收入;
(2)某分析员从2017年至2023年人均可支配收入中,任取3年的数据进行分析,记其中人均可支配收入超过4.5万的年份个数为随机变量X,求X的分布列与数学期望.
参考数据及公式:,,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】由题意,求出剔除后的平均数,进而求出剔除前的平均数,根据回归直线必过样本点中心得到,进而得到,将点代入,即可求解.
【详解】设没剔除两对数据前的平均数分别为,,
剔除两对数据后的平均数分别为,,
因为,
所以,,
则,
所以,
又因为,
所以,
解得.
故选:C.
2.A
【分析】将样本点中心,并代入回归方程,求,并代入后,即可求解残差.
【详解】因为回归直线过样本点中心即,代入,可得,
解得,当时,,所以残差为.
故选:A
3.C
【分析】由题意求出剔除后的平均数,进而求出剔除前的平均数,根据回归直线必过样本点中心,得到,进而得到,将点代入,即可求解.
【详解】设没剔除两对数据前的,的平均数分别为,,
剔除两对数据后的,的平均数分别为,,
因为,所以,则,
因为两对数据为和,所以,
所以,
所以,解得.
故选:C.
4.B
【分析】首先由表示出样本中心点,再代入经验回归方程,计算可得.
【详解】由题可得,
,
因为经验回归直线必过样本中心点,
所以,解得.
故选:B.
5.C
【分析】根据样本中心求解,即可代入求解.
【详解】由表中数据可得,
将代入可得,
故,当时,所以万元,
故选:C
6.A
【分析】利用散点图的规律分析气压与高度、沸点与气压、沸点与海拔高度的相关性即可判定.
【详解】由图1知气压随海拔高度的增加而减小,由图2知沸点随气压的升高而升高,
所以气压与海拔高度呈负相关,沸点与气压呈正相关,沸点与海拔高度呈负相关.
由于两个散点图中的点都呈线性分布,
所以沸点与海拔高度、沸点与气压的相关性都很强,故B,C,D正确,A错误.
故选:A.
7.A
【分析】根据的特点判断斜率和截距;由于去掉,其它点的线性关系更强,从而可判断相关系数.
【详解】身高的平均数为,
因为离群点的横坐标167小于平均值176,纵坐标90相对过大,
所以去掉后经验回归直线的截距变小而斜率变大,故,
去掉后相关性更强,拟合效果也更好,且还是正相关,所以.
故选:A
8.B
【分析】画出散点图,根据线性相关性与偏离程度判断即可.
【详解】根据表格数据,得到散点图如下所示:
由散点图可知数据偏离程度最高,故应该去掉数据.
故选:B
9.AC
【分析】对于A,可利用不等式法求解;对于B,根据正态分布曲线的对称性即可验算;对于C,将样本中心坐标代入回归方程即可验算;对于D,由相关系数的意义即可判断.
【详解】对于,故,
令,解得,故,故A正确;
对于,故错误;
对于,回归直线必过样本中心,可得,解得,故C正确;
对于,两个变量的相关系数为越小,与之间的相关性越弱,故D错误.
故选:AC.
10.BC
【分析】A选项,根据百分位数的运算公式得到答案;B选项,利用平均数定义得到,根据方差的计算公式得到;C选项,由正态分布的对称性得到C正确;D选项,由题意得到,得到D错误.
【详解】A选项,,故从小到大从第4个和第5个数的平均数作为第40百分位数,即,A错误;
B选项,,,
因为,(),故,
故,
,
故,B正确;
C选项,因为,,
关于对称,所以,C正确;
D选项,由题意得,整理得,D错误.
故选:BC
11.BD
【分析】根据题意,结合回归方程的性质,样本均值和方程的计算方法,以及百分位数的计算方法,正态分布的概率计算,逐项判定,即可求解.
【详解】对于A中,根据回归方程经过样本中心,但样本中心不一定是数据中的点,
所以这组数据不一定有,所以A错误;
对于中,样本均值,
样本方差:
,所以B正确
对于C中,将这原来的30个数从小到大排列为,则,
所以原来的分位数为,
若去掉其中最大和最小的数据,剩下28个数据为,则,
以剩下28个数据的分位数为,由于互不相同,所以C不正确;
对于D中,由,
则,所以D正确.
故选:BD.
12.ABC
【分析】根据已知条件,结合变量间的相关关系,结合图象分析判断即可.
【详解】由散点图可知,去掉点后,与的线性相关加强,且为负相关,
所以样本的相关系数变小,残差的平方和变小,样本数据y的平均值变小,故ABC正确;
回归直线中的回归系数变大,故D错误.
故选:ABC.
13.4.5
【分析】表示出样本中心点的横、纵坐标,将其代入回归直线方程即可求解.
【详解】样本中心点的横坐标为,样本中心点的纵坐标为,
所以由样本中心点必在回归方程所对应的直线上,可得,解得.
故答案为:4.5.
14.
【分析】令,只需要求和即可得答案.
【详解】解:令,则,,
则必经过点.
故答案为:.
15.
【分析】根据给定数表求出样本中心点,再代入回归直线求出参数即可求得结果.
【详解】依题意,,,
所以样本中心点坐标为,代入回归方程得,,
解得,
所以回归方程为,
当时,,
即当月销售单价为元件时,月销售量约为万件.
故答案为:
16.40
【分析】线性回归方程中,当,求的值.
【详解】若销售量为80顶,则,解得,所以预计单价应定为40元.
故答案为:40
17.(1),355人;
(2)分布列见解析,.
【分析】(1)由两边取常用对数,利用换元法转化为线性归回直线方程并结合公式进行求解;
(2)根据概率的乘法公式进行求解列出分布列,根据期望公式计算结果.
【详解】(1)由,得,设,,,则.
,
.
把样本中心点代入方程得,
所以,即,
其回归方程为,
当时,.
(2)的可能取值为:.
分布列如下:
0.1 0.35 0.15 0.4
所以,购物的平均费用为:.
18.(1)
(2)(ⅰ)(ⅱ)
【分析】(1)依题意的可能取值为,,,,求出所对应的概率,即可判断;
(2)(ⅰ)对两边取对数,由参考数据可知,根据样本中心点求出,即可求出回归方程,再将代入计算可得;(ⅱ)依题意可得,,再令,求出的取值范围,再由正态分布的性质计算可得.
【详解】(1)依题意,随机变量服从超几何分布,且的可能取值为,,,,
则,,,.
由此可得最大,即的可能性最大,故最有可能的取值为;
(2)(ⅰ)依题意,两边取对数,得,
即,其中,
由提供的参考数据,可知,又,故,
所以,
由提供的参考数据,可得,故,
当时,,即估计其绩效等级优秀率为;
(ⅱ)由(ⅰ)及提供的参考数据可知,,,
又,即,可得,即.
又,且,
由正态分布的性质,得,
记“绩效等级优秀率不低于”为事件,则,
所以绩效等级优秀率不低于的概率等于.
19.(1)
(2)65万元
【分析】(1)根据所给数据求出,然后由求得可得回归方程;
(2)将代入回归方程即可得预测值.
【详解】(1),
.
.
关于的经验回归方程为.
(2)由(1)可得,.
当时,.
对款产品投入30万元年研发费用,年利润约为65万元.
20.(1)X的分布列见解析,期望
(2);预测广告费支出10万元时的销售额为87万元.
【分析】(1)根据超几何分布的概率公式求解分布列,进而可求解期望,
(2)利用最小二乘法求解线性回归方程即可.
【详解】(1)从A,B,C,D,E这5家超市中随机抽取3家,记销售额不少于60万元的超市有C,D,E这3家超市,
则随机变量的可能取值为1,2,3
,,,
的分布列为:
1 2 3
数学期望.
(2),,
,
.
关于的线性回归方程为;
在中,取,得.
预测广告费支出10万元时的销售额为87万元.
21.(1),5.37 万元
(2)分布列见解析,期望为.
【分析】(1)求出相关数据,代入公式得到回归直线方程,并代入即可;
(2)首先得到 的可能取值为 0,1,2,3,分步列出分布列,计算期望即可.
【详解】(1)由题意得,,
,
,
,
故,
,
故回归方程为,
又因为2024年的年份编号为8,将代入,解得,
预测2024年该市城镇居民人均可支配收入为5.37万元;
(2)由图表知,人均可支配收入超过4.5万的年份有3年,
故的可能取值为0,1,2,3,则,
,
,
,
故随机变量的分布列为:
0 1 2 3
故.
答案第1页,共2页
答案第1页,共2页
