19.1.2.2 函数的表示方法同步练习(含答案)
文档属性
| 名称 | 19.1.2.2 函数的表示方法同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 18:24:33 | ||
图片预览




文档简介
19.1 函数
19.1.2 函数的图像
第2课时 函数的表示方法
一、选择题
1.用长为50的栏杆围成一个长为x,宽为y的长方形,则y与x的函数关系式为( )
A.y=25-x B.y=25+x C.y=50-x D.y=50+x
2.李大爷想围成一个如图所示的长方形菜园,已知长方形菜园ABCD的面积为24平方米,设BC边的长为x米,AB边的长为y米,则y与x之间的函数解析式为( )
A.y= B.y=-2x+24 C.y=2x-24 D.y=x-12
第2题图 第4题图 第8题图
3.若每上6个台阶就升高1米,则上升高度h(米)与上的台阶数m(个)之间的函数解析式是( )
A.h=6m B.h=6+m C.h=m-6 D.h=
4.如果两个变量x、y之间的函数关系如图所示,则函数值y的取值范围是( )
A.-3≤y≤3 B.0≤y≤2 C.1≤y≤3 D.0≤y≤3
5.已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时.若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )
A.y=4x(x≥0) B.y=4x-3 C.y=3-4x(x≥0) D.y=3-4x
6.下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( )
华氏°F 23 32 41 a 59
摄氏℃ -5 0 5 10 15
A.45 B.50 C.53 D.68
7.在某次试验中,测得两个变量m和v之间的4组对应数据如表:
m 1 2 3 4
v 3 5 7 9
则m与v之间的关系最接近于下列各关系式中的( )
A.v=2m+1 B.v=m2+2 C.v=m+2 D.v=3m
8.如图所示是某市某一天内的气温变化图,根据图象,下列说法中错误的是( )
A.这一天最高气温是28 ℃
B.这一天中最高气温与最低气温的差为16 ℃
C.这一天中2时至14时之间的气温在逐渐升高
D.这一天中只有14时至24时之间的气温在逐渐降低
9.某学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
支撑物的高度h(cm) 10 20 30 40 50 60 70 80
小车下滑的时间t(s) 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50
下列说法中错误的是( )
A.当h=60 cm时,t=1.71 s B.随着h逐渐升高,t逐渐变小
C.h每增加10 cm,t减小1.23 s D.随着h逐渐升高,小车下滑的平均速度逐渐加快
10.如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)关于销售量x(件)的函数图象.给出下列说法,其中不正确的是( )
A.售2件时,甲、乙两家的售价相同 B.买1件时,买乙家的合算
C.买3件时,买甲家的合算 D.乙家的1件售价约为3元
第10题图 第14题图 第15题图
11.梓毅早晨坐出租车上学,他观察出租车启动之后,先加速行驶一段距离后开始匀速行驶,过了一段时间减速后在十字路口等待红灯,绿灯通行之后开始加速行驶,一段时间后又匀速行驶.如图所示的哪一幅图可以近似刻画出租车这段时间内的速度变化情况( )
二、填空题
12.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表.由表格中y与t的关系可知,当汽车行驶 小时时,油箱的余油量为0.
t(小时) 0 1 2 3
y(升) 120 112 104 96
13.已知变量x,y满足下表的关系:
x … -2 -1 0 1 2 …
y … -6 -3 0 3 6 …
则x,y之间的函数关系式为 .
14.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离(单位:米)与时间(单位:分钟)的对应关系如图所示,则小张骑车的速度为 米/分钟.
15.如图所示,为一个沙漏在计时过程中所剩沙子质量y(克)与时间x(小时)之间关系的图象,则从开始计时到沙子漏光所需的时间为 小时.
16.如图①是两圆柱形连通容器(连通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图②所示,根据提供的图象信息,若甲容器的底面半径为1 cm,则乙容器的底面半径为 2 cm.
三、解答题
17.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20 t,按每吨2.5元收费.如果超过20 t,未超过的部分按每吨2.5元收费,超过的部分按每吨3.3元收费.设某户每月用水量为x t,应缴水费为y元.
(1)分别写出每月用水量未超过20 t和超过20 t时,y与x间的函数关系式;
(2)若该城市某户4月份水费为平均每吨2.8元,求该户4月份用水多少吨?
18.威宁粮食二库需要把晾晒场上的120吨苞谷入库封存.受设备影响,每天只能入库15吨.入库所用的时间为x(单位:天),未入库苞谷数量为y(单位:吨).
(1)直接写出y和x间的关系式为: ;
(2)二库职工经过钻研,改进了入库设备,现在每天能比原来多入库5吨.则
①直接写出现在y和x间的关系式为: ;
②求将120吨苞谷入库封存所需天数现在比原来少多少天?
19.根据记录,从地面向上11 km以内,每升高1 km,气温降低6 ℃.又知在距离地面11 km以上的高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11 km以内的y与x之间的关系式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26 ℃时,飞机距离地面的高度为7 km,求当时这架飞机下方地面的气温;小敏想:假如飞机当时在距离地面12 km的高空,飞机外的气温是多少呢?请求出当飞机距离地面12 km时,飞机外的气温.
20.织金县某学校团支部书记暑假带领该校“优等生”去旅游,甲旅游社说:“若团支部书记买全票一张,则学生可享受半价优惠”.乙旅行社说:“包括团支部书记在内都6折优惠”.若全票价是1 200元,设学生人数为x,甲旅行社收费为y甲、乙旅行社收费为y乙.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)当学生人数是多少时,两家旅行社的收费是一样的?
21.声音在空气中传播的速度(简称“声速”)和气温有如下表中的关系:
气温/℃ 0 5 10 15 20
声速/(m/s) 331 334 337 340 343
(1)上表反映了 之间的关系,其中 是自变量, 是 的函数;
(2)若用T(℃)表示气温,v(m/s)表示声速,则随着T的增大,v将发生怎样的变化?
(3)根据表中数据的变化,你发现了什么规律?写出v与T之间的函数解析式(不需要写自变量的取值范围);
(4)根据你发现的规律,回答下列问题:在30 ℃发生闪电的夏夜,小明在看到闪电6 s后听到雷声,那么发生打雷的地方距小明大约有多远?(光传播的时间可忽略不计)
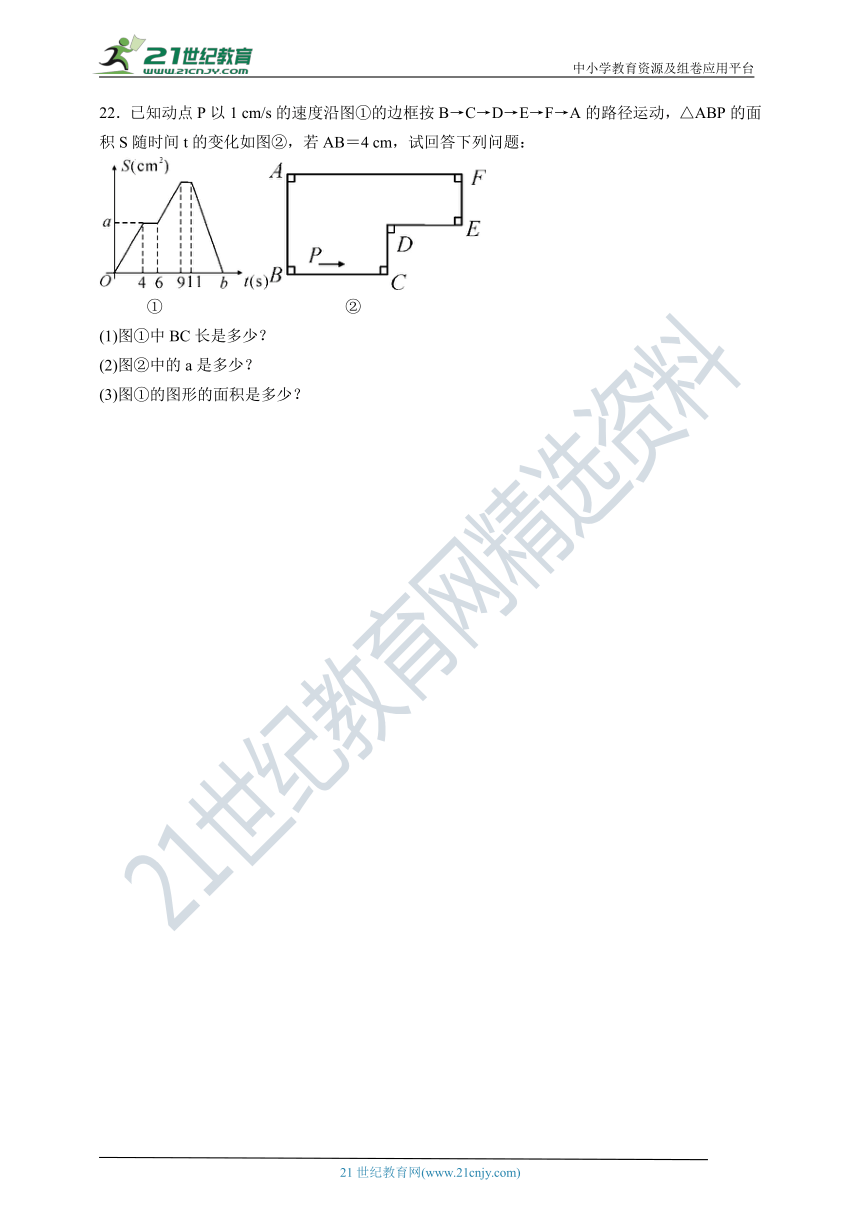
22.已知动点P以1 cm/s的速度沿图①的边框按B→C→D→E→F→A的路径运动,△ABP的面积S随时间t的变化如图②,若AB=4 cm,试回答下列问题:
① ②
(1)图①中BC长是多少?
(2)图②中的a是多少?
(3)图①的图形的面积是多少?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.用长为50的栏杆围成一个长为x,宽为y的长方形,则y与x的函数关系式为( A )
A.y=25-x B.y=25+x C.y=50-x D.y=50+x
2.李大爷想围成一个如图所示的长方形菜园,已知长方形菜园ABCD的面积为24平方米,设BC边的长为x米,AB边的长为y米,则y与x之间的函数解析式为( A )
A.y= B.y=-2x+24 C.y=2x-24 D.y=x-12
第2题图 第4题图 第8题图
3.若每上6个台阶就升高1米,则上升高度h(米)与上的台阶数m(个)之间的函数解析式是( D )
A.h=6m B.h=6+m C.h=m-6 D.h=
4.如果两个变量x、y之间的函数关系如图所示,则函数值y的取值范围是( D )
A.-3≤y≤3 B.0≤y≤2 C.1≤y≤3 D.0≤y≤3
5.已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时.若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( D )
A.y=4x(x≥0) B.y=4x-3 C.y=3-4x(x≥0) D.y=3-4x
6.下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( B )
华氏°F 23 32 41 a 59
摄氏℃ -5 0 5 10 15
A.45 B.50 C.53 D.68
7.在某次试验中,测得两个变量m和v之间的4组对应数据如表:
m 1 2 3 4
v 3 5 7 9
则m与v之间的关系最接近于下列各关系式中的( A )
A.v=2m+1 B.v=m2+2 C.v=m+2 D.v=3m
8.如图所示是某市某一天内的气温变化图,根据图象,下列说法中错误的是( D )
A.这一天最高气温是28 ℃
B.这一天中最高气温与最低气温的差为16 ℃
C.这一天中2时至14时之间的气温在逐渐升高
D.这一天中只有14时至24时之间的气温在逐渐降低
9.某学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
支撑物的高度h(cm) 10 20 30 40 50 60 70 80
小车下滑的时间t(s) 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50
下列说法中错误的是( C )
A.当h=60 cm时,t=1.71 s B.随着h逐渐升高,t逐渐变小
C.h每增加10 cm,t减小1.23 s D.随着h逐渐升高,小车下滑的平均速度逐渐加快
10.如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)关于销售量x(件)的函数图象.给出下列说法,其中不正确的是( D )
A.售2件时,甲、乙两家的售价相同 B.买1件时,买乙家的合算
C.买3件时,买甲家的合算 D.乙家的1件售价约为3元
第10题图 第14题图 第15题图
11.梓毅早晨坐出租车上学,他观察出租车启动之后,先加速行驶一段距离后开始匀速行驶,过了一段时间减速后在十字路口等待红灯,绿灯通行之后开始加速行驶,一段时间后又匀速行驶.如图所示的哪一幅图可以近似刻画出租车这段时间内的速度变化情况( C )
二、填空题
12.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表.由表格中y与t的关系可知,当汽车行驶 小时时,油箱的余油量为0.
t(小时) 0 1 2 3
y(升) 120 112 104 96
【答案】15
13.已知变量x,y满足下表的关系:
x … -2 -1 0 1 2 …
y … -6 -3 0 3 6 …
则x,y之间的函数关系式为 .
【答案】y=3x
14.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离(单位:米)与时间(单位:分钟)的对应关系如图所示,则小张骑车的速度为 米/分钟.
【答案】300
15.如图所示,为一个沙漏在计时过程中所剩沙子质量y(克)与时间x(小时)之间关系的图象,则从开始计时到沙子漏光所需的时间为 小时.
【答案】
16.如图①是两圆柱形连通容器(连通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图②所示,根据提供的图象信息,若甲容器的底面半径为1 cm,则乙容器的底面半径为 2 cm.
【答案】2
【解析】观察函数图象可知,乙容器底面积为甲容器底面积的4倍,∴乙容器底面半径为2 cm.
三、解答题
17.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20 t,按每吨2.5元收费.如果超过20 t,未超过的部分按每吨2.5元收费,超过的部分按每吨3.3元收费.设某户每月用水量为x t,应缴水费为y元.
(1)分别写出每月用水量未超过20 t和超过20 t时,y与x间的函数关系式;
(2)若该城市某户4月份水费为平均每吨2.8元,求该户4月份用水多少吨?
解:(1)当x≤20时,y=2.5x;
当x>20时,
y=3.3(x-20)+2.5×20=3.3x-16.
(2)由题意知,该户4月份用水超过了20 t.
设该户4月份用水a t,得
2.8a=3.3a-16,解得a=32.
答:该户4月份用水32 t.
18.威宁粮食二库需要把晾晒场上的120吨苞谷入库封存.受设备影响,每天只能入库15吨.入库所用的时间为x(单位:天),未入库苞谷数量为y(单位:吨).
(1)直接写出y和x间的关系式为: ;
【答案】y=120-15x
(2)二库职工经过钻研,改进了入库设备,现在每天能比原来多入库5吨.则
①直接写出现在y和x间的关系式为: ;
【答案】y=120-20x
②求将120吨苞谷入库封存所需天数现在比原来少多少天?
解:(2)②-=2(天).
答:将120吨苞谷入库封存所需天数现在比原来少2天.
19.根据记录,从地面向上11 km以内,每升高1 km,气温降低6 ℃.又知在距离地面11 km以上的高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11 km以内的y与x之间的关系式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26 ℃时,飞机距离地面的高度为7 km,求当时这架飞机下方地面的气温;小敏想:假如飞机当时在距离地面12 km的高空,飞机外的气温是多少呢?请求出当飞机距离地面12 km时,飞机外的气温.
解:(1)y=m-6x(0≤x<11).
(2)将x=7,y=-26代入y=m-6x,得
-26=m-42,∴m=16,
∴当时地面的气温为16 ℃.
∵x=12>11,∴y=16-6×11=-50(℃),
∴当飞机距离地面12 km时,飞机外的气温为-50 ℃.
20.织金县某学校团支部书记暑假带领该校“优等生”去旅游,甲旅游社说:“若团支部书记买全票一张,则学生可享受半价优惠”.乙旅行社说:“包括团支部书记在内都6折优惠”.若全票价是1 200元,设学生人数为x,甲旅行社收费为y甲、乙旅行社收费为y乙.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)当学生人数是多少时,两家旅行社的收费是一样的?
解:(1)设学生人数为x人,由题意,得
y甲=0.5×1200x+1200=600x+1200,
y乙=0.6×1200x+0.6×1200=720x+720.
(2)由题意,得当y甲=y乙时,
600x+1200=720x+720,解得x=4,
故当学生人数是4人时,两家旅行社的收费是一样的.
21.声音在空气中传播的速度(简称“声速”)和气温有如下表中的关系:
气温/℃ 0 5 10 15 20
声速/(m/s) 331 334 337 340 343
(1)上表反映了 之间的关系,其中 是自变量, 是 的函数;
【答案】声速与气温 气温 声速 气温
(2)若用T(℃)表示气温,v(m/s)表示声速,则随着T的增大,v将发生怎样的变化?
(3)根据表中数据的变化,你发现了什么规律?写出v与T之间的函数解析式(不需要写自变量的取值范围);
(4)根据你发现的规律,回答下列问题:在30 ℃发生闪电的夏夜,小明在看到闪电6 s后听到雷声,那么发生打雷的地方距小明大约有多远?(光传播的时间可忽略不计)
解:(2)随着T的增大,v也逐渐增大.
(3)v=331+T.
(4)v=331+×30=349,
s=349×6=2094(m).
∴发生打雷的地方距小明大约有2094 m.
22.已知动点P以1 cm/s的速度沿图①的边框按B→C→D→E→F→A的路径运动,△ABP的面积S随时间t的变化如图②,若AB=4 cm,试回答下列问题:
① ②
(1)图①中BC长是多少?
(2)图②中的a是多少?
(3)图①的图形的面积是多少?
解:(1)图①中的BC长是1×4=4(cm).
(2)由(1)可得,BC=4 cm,
则a=×BC×AB=8 cm2,图②中的a是8.
(3)由图可得CD=(6-4)×1=2(cm),
DE=(9-6)×1=3(cm),
EF=(11-9)×1=2(cm),
则AF=BC+DE=7 cm,又∵AB=4 cm,
∴图①的图形的面积为
AB×AF-CD×DE=4×7-2×3=22(cm2).
19.1.2 函数的图像
第2课时 函数的表示方法
一、选择题
1.用长为50的栏杆围成一个长为x,宽为y的长方形,则y与x的函数关系式为( )
A.y=25-x B.y=25+x C.y=50-x D.y=50+x
2.李大爷想围成一个如图所示的长方形菜园,已知长方形菜园ABCD的面积为24平方米,设BC边的长为x米,AB边的长为y米,则y与x之间的函数解析式为( )
A.y= B.y=-2x+24 C.y=2x-24 D.y=x-12
第2题图 第4题图 第8题图
3.若每上6个台阶就升高1米,则上升高度h(米)与上的台阶数m(个)之间的函数解析式是( )
A.h=6m B.h=6+m C.h=m-6 D.h=
4.如果两个变量x、y之间的函数关系如图所示,则函数值y的取值范围是( )
A.-3≤y≤3 B.0≤y≤2 C.1≤y≤3 D.0≤y≤3
5.已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时.若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )
A.y=4x(x≥0) B.y=4x-3 C.y=3-4x(x≥0) D.y=3-4x
6.下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( )
华氏°F 23 32 41 a 59
摄氏℃ -5 0 5 10 15
A.45 B.50 C.53 D.68
7.在某次试验中,测得两个变量m和v之间的4组对应数据如表:
m 1 2 3 4
v 3 5 7 9
则m与v之间的关系最接近于下列各关系式中的( )
A.v=2m+1 B.v=m2+2 C.v=m+2 D.v=3m
8.如图所示是某市某一天内的气温变化图,根据图象,下列说法中错误的是( )
A.这一天最高气温是28 ℃
B.这一天中最高气温与最低气温的差为16 ℃
C.这一天中2时至14时之间的气温在逐渐升高
D.这一天中只有14时至24时之间的气温在逐渐降低
9.某学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
支撑物的高度h(cm) 10 20 30 40 50 60 70 80
小车下滑的时间t(s) 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50
下列说法中错误的是( )
A.当h=60 cm时,t=1.71 s B.随着h逐渐升高,t逐渐变小
C.h每增加10 cm,t减小1.23 s D.随着h逐渐升高,小车下滑的平均速度逐渐加快
10.如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)关于销售量x(件)的函数图象.给出下列说法,其中不正确的是( )
A.售2件时,甲、乙两家的售价相同 B.买1件时,买乙家的合算
C.买3件时,买甲家的合算 D.乙家的1件售价约为3元
第10题图 第14题图 第15题图
11.梓毅早晨坐出租车上学,他观察出租车启动之后,先加速行驶一段距离后开始匀速行驶,过了一段时间减速后在十字路口等待红灯,绿灯通行之后开始加速行驶,一段时间后又匀速行驶.如图所示的哪一幅图可以近似刻画出租车这段时间内的速度变化情况( )
二、填空题
12.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表.由表格中y与t的关系可知,当汽车行驶 小时时,油箱的余油量为0.
t(小时) 0 1 2 3
y(升) 120 112 104 96
13.已知变量x,y满足下表的关系:
x … -2 -1 0 1 2 …
y … -6 -3 0 3 6 …
则x,y之间的函数关系式为 .
14.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离(单位:米)与时间(单位:分钟)的对应关系如图所示,则小张骑车的速度为 米/分钟.
15.如图所示,为一个沙漏在计时过程中所剩沙子质量y(克)与时间x(小时)之间关系的图象,则从开始计时到沙子漏光所需的时间为 小时.
16.如图①是两圆柱形连通容器(连通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图②所示,根据提供的图象信息,若甲容器的底面半径为1 cm,则乙容器的底面半径为 2 cm.
三、解答题
17.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20 t,按每吨2.5元收费.如果超过20 t,未超过的部分按每吨2.5元收费,超过的部分按每吨3.3元收费.设某户每月用水量为x t,应缴水费为y元.
(1)分别写出每月用水量未超过20 t和超过20 t时,y与x间的函数关系式;
(2)若该城市某户4月份水费为平均每吨2.8元,求该户4月份用水多少吨?
18.威宁粮食二库需要把晾晒场上的120吨苞谷入库封存.受设备影响,每天只能入库15吨.入库所用的时间为x(单位:天),未入库苞谷数量为y(单位:吨).
(1)直接写出y和x间的关系式为: ;
(2)二库职工经过钻研,改进了入库设备,现在每天能比原来多入库5吨.则
①直接写出现在y和x间的关系式为: ;
②求将120吨苞谷入库封存所需天数现在比原来少多少天?
19.根据记录,从地面向上11 km以内,每升高1 km,气温降低6 ℃.又知在距离地面11 km以上的高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11 km以内的y与x之间的关系式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26 ℃时,飞机距离地面的高度为7 km,求当时这架飞机下方地面的气温;小敏想:假如飞机当时在距离地面12 km的高空,飞机外的气温是多少呢?请求出当飞机距离地面12 km时,飞机外的气温.
20.织金县某学校团支部书记暑假带领该校“优等生”去旅游,甲旅游社说:“若团支部书记买全票一张,则学生可享受半价优惠”.乙旅行社说:“包括团支部书记在内都6折优惠”.若全票价是1 200元,设学生人数为x,甲旅行社收费为y甲、乙旅行社收费为y乙.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)当学生人数是多少时,两家旅行社的收费是一样的?
21.声音在空气中传播的速度(简称“声速”)和气温有如下表中的关系:
气温/℃ 0 5 10 15 20
声速/(m/s) 331 334 337 340 343
(1)上表反映了 之间的关系,其中 是自变量, 是 的函数;
(2)若用T(℃)表示气温,v(m/s)表示声速,则随着T的增大,v将发生怎样的变化?
(3)根据表中数据的变化,你发现了什么规律?写出v与T之间的函数解析式(不需要写自变量的取值范围);
(4)根据你发现的规律,回答下列问题:在30 ℃发生闪电的夏夜,小明在看到闪电6 s后听到雷声,那么发生打雷的地方距小明大约有多远?(光传播的时间可忽略不计)
22.已知动点P以1 cm/s的速度沿图①的边框按B→C→D→E→F→A的路径运动,△ABP的面积S随时间t的变化如图②,若AB=4 cm,试回答下列问题:
① ②
(1)图①中BC长是多少?
(2)图②中的a是多少?
(3)图①的图形的面积是多少?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.用长为50的栏杆围成一个长为x,宽为y的长方形,则y与x的函数关系式为( A )
A.y=25-x B.y=25+x C.y=50-x D.y=50+x
2.李大爷想围成一个如图所示的长方形菜园,已知长方形菜园ABCD的面积为24平方米,设BC边的长为x米,AB边的长为y米,则y与x之间的函数解析式为( A )
A.y= B.y=-2x+24 C.y=2x-24 D.y=x-12
第2题图 第4题图 第8题图
3.若每上6个台阶就升高1米,则上升高度h(米)与上的台阶数m(个)之间的函数解析式是( D )
A.h=6m B.h=6+m C.h=m-6 D.h=
4.如果两个变量x、y之间的函数关系如图所示,则函数值y的取值范围是( D )
A.-3≤y≤3 B.0≤y≤2 C.1≤y≤3 D.0≤y≤3
5.已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时.若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( D )
A.y=4x(x≥0) B.y=4x-3 C.y=3-4x(x≥0) D.y=3-4x
6.下表是摄氏温度和华氏温度之间的对应表,则字母a的值是( B )
华氏°F 23 32 41 a 59
摄氏℃ -5 0 5 10 15
A.45 B.50 C.53 D.68
7.在某次试验中,测得两个变量m和v之间的4组对应数据如表:
m 1 2 3 4
v 3 5 7 9
则m与v之间的关系最接近于下列各关系式中的( A )
A.v=2m+1 B.v=m2+2 C.v=m+2 D.v=3m
8.如图所示是某市某一天内的气温变化图,根据图象,下列说法中错误的是( D )
A.这一天最高气温是28 ℃
B.这一天中最高气温与最低气温的差为16 ℃
C.这一天中2时至14时之间的气温在逐渐升高
D.这一天中只有14时至24时之间的气温在逐渐降低
9.某学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
支撑物的高度h(cm) 10 20 30 40 50 60 70 80
小车下滑的时间t(s) 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50
下列说法中错误的是( C )
A.当h=60 cm时,t=1.71 s B.随着h逐渐升高,t逐渐变小
C.h每增加10 cm,t减小1.23 s D.随着h逐渐升高,小车下滑的平均速度逐渐加快
10.如图所示的是甲、乙两家商店销售同一种产品的销售价y(元)关于销售量x(件)的函数图象.给出下列说法,其中不正确的是( D )
A.售2件时,甲、乙两家的售价相同 B.买1件时,买乙家的合算
C.买3件时,买甲家的合算 D.乙家的1件售价约为3元
第10题图 第14题图 第15题图
11.梓毅早晨坐出租车上学,他观察出租车启动之后,先加速行驶一段距离后开始匀速行驶,过了一段时间减速后在十字路口等待红灯,绿灯通行之后开始加速行驶,一段时间后又匀速行驶.如图所示的哪一幅图可以近似刻画出租车这段时间内的速度变化情况( C )
二、填空题
12.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表.由表格中y与t的关系可知,当汽车行驶 小时时,油箱的余油量为0.
t(小时) 0 1 2 3
y(升) 120 112 104 96
【答案】15
13.已知变量x,y满足下表的关系:
x … -2 -1 0 1 2 …
y … -6 -3 0 3 6 …
则x,y之间的函数关系式为 .
【答案】y=3x
14.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离(单位:米)与时间(单位:分钟)的对应关系如图所示,则小张骑车的速度为 米/分钟.
【答案】300
15.如图所示,为一个沙漏在计时过程中所剩沙子质量y(克)与时间x(小时)之间关系的图象,则从开始计时到沙子漏光所需的时间为 小时.
【答案】
16.如图①是两圆柱形连通容器(连通处体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图②所示,根据提供的图象信息,若甲容器的底面半径为1 cm,则乙容器的底面半径为 2 cm.
【答案】2
【解析】观察函数图象可知,乙容器底面积为甲容器底面积的4倍,∴乙容器底面半径为2 cm.
三、解答题
17.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20 t,按每吨2.5元收费.如果超过20 t,未超过的部分按每吨2.5元收费,超过的部分按每吨3.3元收费.设某户每月用水量为x t,应缴水费为y元.
(1)分别写出每月用水量未超过20 t和超过20 t时,y与x间的函数关系式;
(2)若该城市某户4月份水费为平均每吨2.8元,求该户4月份用水多少吨?
解:(1)当x≤20时,y=2.5x;
当x>20时,
y=3.3(x-20)+2.5×20=3.3x-16.
(2)由题意知,该户4月份用水超过了20 t.
设该户4月份用水a t,得
2.8a=3.3a-16,解得a=32.
答:该户4月份用水32 t.
18.威宁粮食二库需要把晾晒场上的120吨苞谷入库封存.受设备影响,每天只能入库15吨.入库所用的时间为x(单位:天),未入库苞谷数量为y(单位:吨).
(1)直接写出y和x间的关系式为: ;
【答案】y=120-15x
(2)二库职工经过钻研,改进了入库设备,现在每天能比原来多入库5吨.则
①直接写出现在y和x间的关系式为: ;
【答案】y=120-20x
②求将120吨苞谷入库封存所需天数现在比原来少多少天?
解:(2)②-=2(天).
答:将120吨苞谷入库封存所需天数现在比原来少2天.
19.根据记录,从地面向上11 km以内,每升高1 km,气温降低6 ℃.又知在距离地面11 km以上的高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11 km以内的y与x之间的关系式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26 ℃时,飞机距离地面的高度为7 km,求当时这架飞机下方地面的气温;小敏想:假如飞机当时在距离地面12 km的高空,飞机外的气温是多少呢?请求出当飞机距离地面12 km时,飞机外的气温.
解:(1)y=m-6x(0≤x<11).
(2)将x=7,y=-26代入y=m-6x,得
-26=m-42,∴m=16,
∴当时地面的气温为16 ℃.
∵x=12>11,∴y=16-6×11=-50(℃),
∴当飞机距离地面12 km时,飞机外的气温为-50 ℃.
20.织金县某学校团支部书记暑假带领该校“优等生”去旅游,甲旅游社说:“若团支部书记买全票一张,则学生可享受半价优惠”.乙旅行社说:“包括团支部书记在内都6折优惠”.若全票价是1 200元,设学生人数为x,甲旅行社收费为y甲、乙旅行社收费为y乙.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)当学生人数是多少时,两家旅行社的收费是一样的?
解:(1)设学生人数为x人,由题意,得
y甲=0.5×1200x+1200=600x+1200,
y乙=0.6×1200x+0.6×1200=720x+720.
(2)由题意,得当y甲=y乙时,
600x+1200=720x+720,解得x=4,
故当学生人数是4人时,两家旅行社的收费是一样的.
21.声音在空气中传播的速度(简称“声速”)和气温有如下表中的关系:
气温/℃ 0 5 10 15 20
声速/(m/s) 331 334 337 340 343
(1)上表反映了 之间的关系,其中 是自变量, 是 的函数;
【答案】声速与气温 气温 声速 气温
(2)若用T(℃)表示气温,v(m/s)表示声速,则随着T的增大,v将发生怎样的变化?
(3)根据表中数据的变化,你发现了什么规律?写出v与T之间的函数解析式(不需要写自变量的取值范围);
(4)根据你发现的规律,回答下列问题:在30 ℃发生闪电的夏夜,小明在看到闪电6 s后听到雷声,那么发生打雷的地方距小明大约有多远?(光传播的时间可忽略不计)
解:(2)随着T的增大,v也逐渐增大.
(3)v=331+T.
(4)v=331+×30=349,
s=349×6=2094(m).
∴发生打雷的地方距小明大约有2094 m.
22.已知动点P以1 cm/s的速度沿图①的边框按B→C→D→E→F→A的路径运动,△ABP的面积S随时间t的变化如图②,若AB=4 cm,试回答下列问题:
① ②
(1)图①中BC长是多少?
(2)图②中的a是多少?
(3)图①的图形的面积是多少?
解:(1)图①中的BC长是1×4=4(cm).
(2)由(1)可得,BC=4 cm,
则a=×BC×AB=8 cm2,图②中的a是8.
(3)由图可得CD=(6-4)×1=2(cm),
DE=(9-6)×1=3(cm),
EF=(11-9)×1=2(cm),
则AF=BC+DE=7 cm,又∵AB=4 cm,
∴图①的图形的面积为
AB×AF-CD×DE=4×7-2×3=22(cm2).
