1.1.1任意角
图片预览







文档简介
课件35张PPT。问题一:
初中角的概念是如何定义的呢?
问题二:
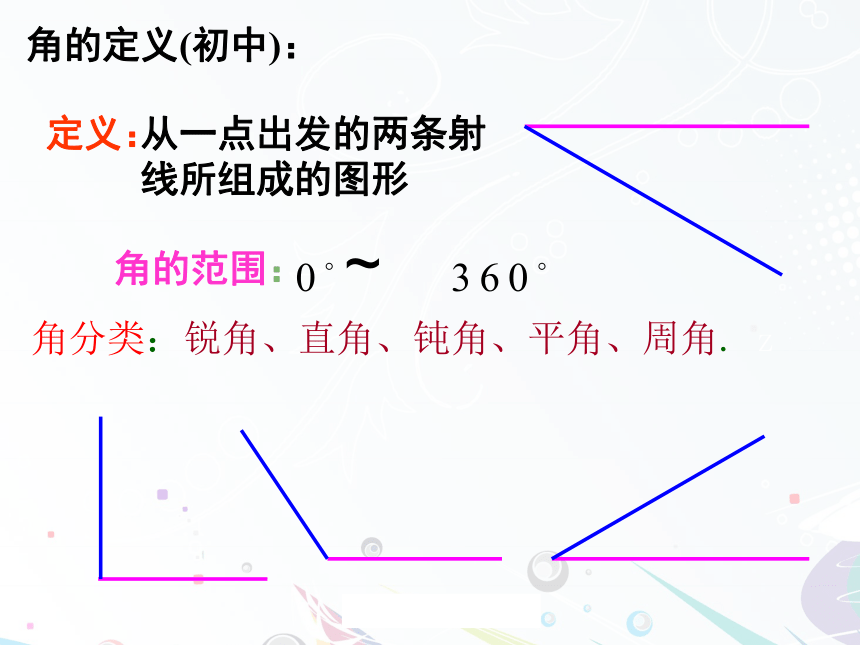
常见的角度有哪些?角的取值范围是从多少度到多少度?角的定义(初中):定义:从一点出发的两条射
线所组成的图形角的范围:~角分类:锐角、直角、钝角、平角、周角. z你的手表慢了5分钟,你是怎样将它校准的?分针应该旋转多少度?假如你的手表快了1.25小时,你应当如何将它校准?
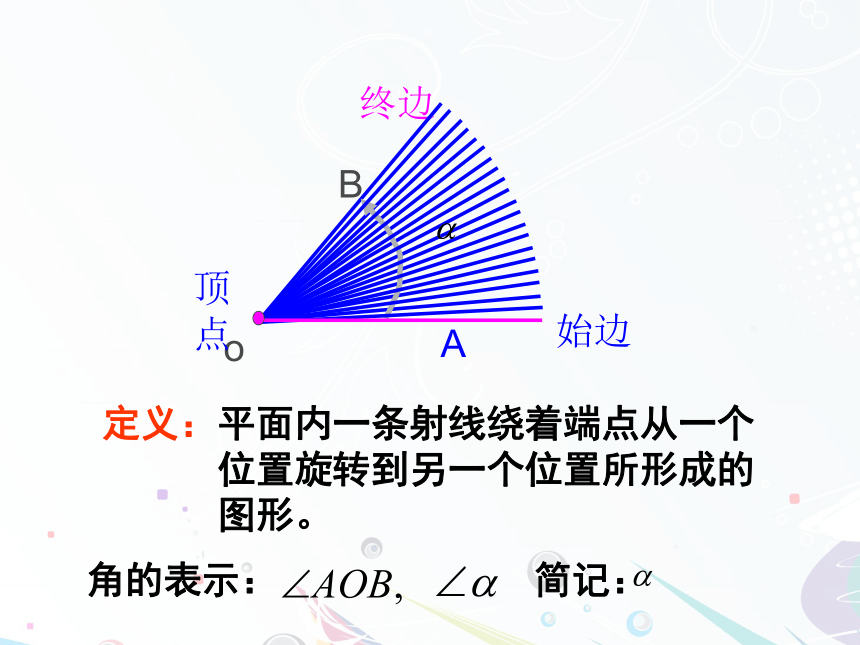
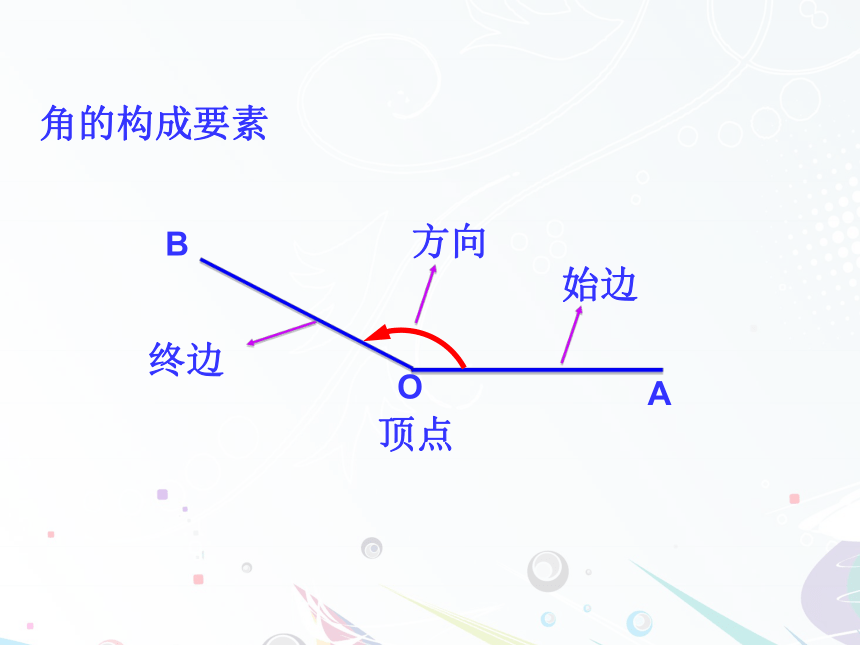
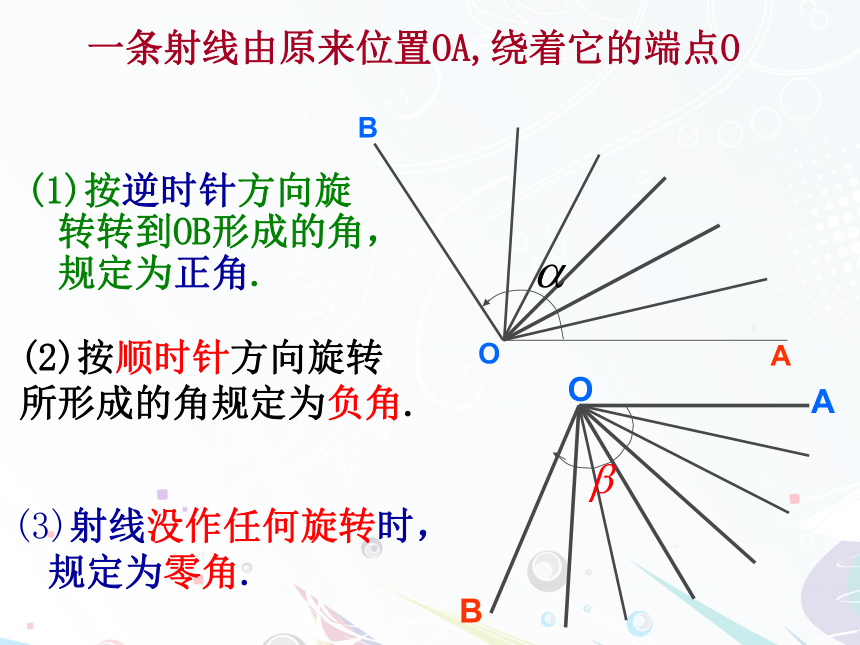
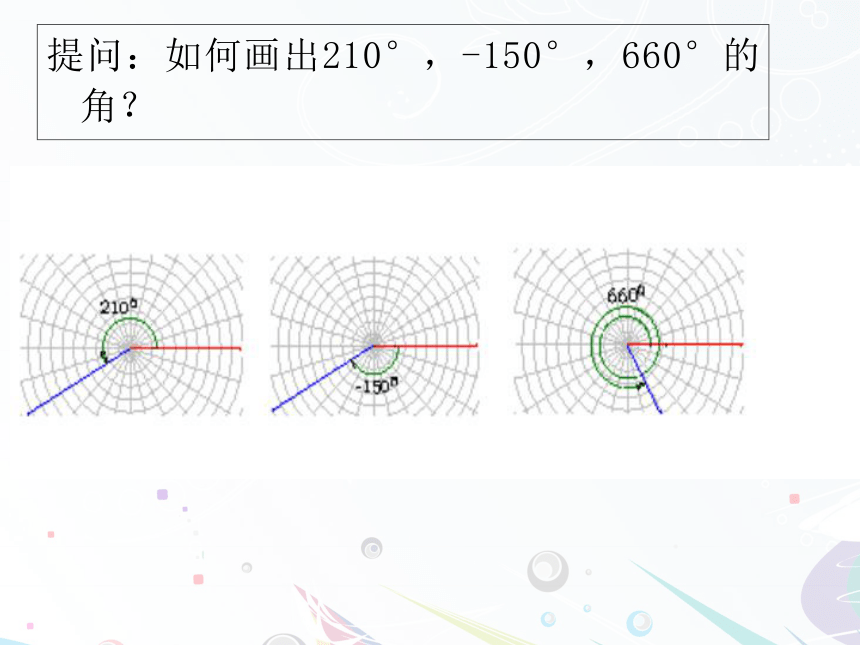
当时间校准后,分针旋转了多少度?思考:跳水运动员向内、向外转体两周半,这是多大角度?体操中有转体两周或转体两周半,如何度量这些角度呢?关键是用运动的观点来看待角的变化.这些例子不仅不在0°~360°范围内,而且有方向,如何解决这一问题?有必要将角的概念及范围推广1.1.1 任意角oAB始边 终边顶点定义:平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形。 角的表示:简记:角的构成要素始边终边顶点ABO方向B一条射线由原来位置OA,绕着它的端点O(2)按顺时针方向旋转所形成的角规定为负角.OAB(3)射线没作任何旋转时,规定为零角.(1)按逆时针方向旋转转到OB形成的角,规定为正角.提问:如何画出210°,-150°,660°的角?3.射线OA与x轴非负半轴重合,绕端点O逆时针旋转100°到达OB位置,OB绕端点O顺时针旋转230°到达OC位置,则∠AOC=( )
A.330° B.130° C.-130° D.不能确定C全优第3页基础夯实6.已知角α在0°~360°内,并且α的终边与 -50°角的终边关于x轴对称,则α=________.50°全优第3页能力提高xyo 1)置角的顶点于原点终边落在第几象限就是第几象限角2)始边重合于X轴的正半轴 Ⅰ Ⅱ Ⅲ Ⅳ
象限角:练习:课本:P5 3(1)(2),1角的终边在坐标轴上的角(角的终边不在任何象限的角),思考:90°是第一象限角?为什么?思考:小于90°的角是锐角吗?为什么?轴线角:如果角的终边落在坐标轴上,就说该角不属于任何象限,习惯上称其为轴线角.思考:锐角与第一象限的角是什么关系?
钝角与第二象限的角是什么关系?
直角与轴线角是什么关系?锐角一定是第一象限的角,第一象限角不一定是锐角.钝角一定是第二象限的角,第二象限角不一定是钝角.直角一定是轴线角,轴线角不一定是直角.思考:第二象限的角一定比第一象限的角大吗? 象限角只能反映角的终边所在象限,不能反映角的大小. 思考:一个角的角度一旦确定,其终边位置可否确定?思考:一个角的终边确定,其角度可否确定下来?1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A,B,C的关系是( )
A.B=A∩C B.B∪C=C
C.A?C D.A=B=CB全优83页限时规范训练4.若α是第四象限的角,则180°-α是第______象限的角.三【解析】∵α是第四象限的角,∴-α是第一象限角, 则由任意角的定义知,180°-α是第三象限角.【例】 在坐标系中画出下列各角,观察它们的终边具有什么关系?任意两角的关系是什么呢?
-32°,328°,-392°-32°-392°o328°解答:各角的终边相同思考:它们的终边具有什么关系呢?思考:终边相同的角间具有什么关系呢? 如何表示与∠α终边相同的角呢?-32°,328°,-392°思考:所有与-32°角终边相同的角,连同-32°
角在内,可构成一个集合S,你能用描述
法表示集合S吗? 终边相同的角所有与 终边相同的角,连同 在内都可以写成 (k 是整数)的形式 . 终边相同的二角相差360度的整数倍练习:课本5页 2所以与 角终边相同的角是 ,它是第二象限角.练习:课本5页 4(2)(3)7.已知角α=-1 000°,则与α终边相同的最小正角是________.80°【解析】∵-1 000°=-3×360°+80°,∴80°与-1 000°终边相同.又终边相同的两个角相差360°的整数倍,∴在[0°,360°)上,只有80°与-1 000°终边相同,∴与-1 000°终边相同的最小正角是80°.全优第3页能力提高5.如果θ为小于360°的正角且这个角θ的4倍角即4θ与这个角的终边重合,求θ的值.【解析】由题意得4θ=θ+k×360°(k∈Z),即θ=k×120°,而θ为小于360°的正角,所以θ的值为120°或240°.全优83页限时规范训练例2 写出终边在y轴上的角的集合。解: 0o~360o内,终边在y轴上的角有900,2700S1={β| β=900+k?3600,k∈Z} ={β| β= 900+(2k)?1800, k∈Z}S2={β| β=2700+k?3600,k∈Z}={β| β= 900+1800+2k?1800, k∈Z}={β| β= 900+(2k+1)1800 ,k∈Z}S=S1∪S2={β|β=900+k?1800 ,k∈Z}所以, 终边在y轴上的角的集合:例题补充:终边在x轴上的角的集合?例2:写出终边在Y轴上的角的集合:思路一:分正负半轴两种情况分析。思路二:Y轴可以看成是X轴按逆时针
旋转90°得到。终边在坐标轴上角的取值0090018002700 +K*3600+K*3600+K*3600+K*3600或3600+K*3600思考:如何表示象限角?象限角的表示:解:终边在射线 y = x 正方向上的角的集合是
A={ }终边在终边在射线 y= x负方向上的角的集合是
B={ }所以终边在y=x上的角的集合是S中适合 的元素是
45°-2×180°= -315° 45°-1×180°= -135°
45°+0×180°= 45° 45°+1×180°= 225°
45°+2×180°= 405° 45°+3×180°= 585°练习:课本5页 5(2)2.写出与角60°的终边在一条直线上的角的集合.【解析】在0°~360°内,与角60°的终边在一条直线上的角是60°与240°. 故与角60°的终边在一条直线上的角的集合是S={α|α=k×360°+60°,k∈Z}∪{α|α=k×360°+240°,k∈Z} ={α|α=2k×180°+60°,k∈Z}∪{α|α=2k×180°+180°+60°,k∈Z}={α|α=2k×180°+60°,k∈Z}∪{α|α=(2k+1)×180°+60°,k∈Z}={α|α=n×180°+60°,n∈Z}.全优第2页变式训练y=xS={β|β=450+k?1800 ,k∈Z}练习: 写出终边在如图位置的角的集合:练习:课本10页 5(2)2.下列表示中不正确的是( )
A.终边在坐标轴上的角的集合是{α|α=k×90°,k∈Z}
B.与-50°的终边相同的角的集合是{α|α=k×360°+310°,k∈Z}
C.终边在第二、四象限的角平分线上的角的集合是{α|α=k×360°-45°,k∈Z}
D.终边在直线y=x上的角的集合是{α|α=k×180°+45°,k∈Z}C全优83页限时规范训练3.如图所示的阴影部分是45°角(终边为OA)与300°角(终边为OB)的终边所夹的区域,试写出阴影区域内的角的集合(虚线表示不含边界).【解析】阴影区域内的角的集合是
S={α|k×360°-60°≤α≤k×360°+45°,k∈Z}.全优第3页变式训练
初中角的概念是如何定义的呢?
问题二:
常见的角度有哪些?角的取值范围是从多少度到多少度?角的定义(初中):定义:从一点出发的两条射
线所组成的图形角的范围:~角分类:锐角、直角、钝角、平角、周角. z你的手表慢了5分钟,你是怎样将它校准的?分针应该旋转多少度?假如你的手表快了1.25小时,你应当如何将它校准?
当时间校准后,分针旋转了多少度?思考:跳水运动员向内、向外转体两周半,这是多大角度?体操中有转体两周或转体两周半,如何度量这些角度呢?关键是用运动的观点来看待角的变化.这些例子不仅不在0°~360°范围内,而且有方向,如何解决这一问题?有必要将角的概念及范围推广1.1.1 任意角oAB始边 终边顶点定义:平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形。 角的表示:简记:角的构成要素始边终边顶点ABO方向B一条射线由原来位置OA,绕着它的端点O(2)按顺时针方向旋转所形成的角规定为负角.OAB(3)射线没作任何旋转时,规定为零角.(1)按逆时针方向旋转转到OB形成的角,规定为正角.提问:如何画出210°,-150°,660°的角?3.射线OA与x轴非负半轴重合,绕端点O逆时针旋转100°到达OB位置,OB绕端点O顺时针旋转230°到达OC位置,则∠AOC=( )
A.330° B.130° C.-130° D.不能确定C全优第3页基础夯实6.已知角α在0°~360°内,并且α的终边与 -50°角的终边关于x轴对称,则α=________.50°全优第3页能力提高xyo 1)置角的顶点于原点终边落在第几象限就是第几象限角2)始边重合于X轴的正半轴 Ⅰ Ⅱ Ⅲ Ⅳ
象限角:练习:课本:P5 3(1)(2),1角的终边在坐标轴上的角(角的终边不在任何象限的角),思考:90°是第一象限角?为什么?思考:小于90°的角是锐角吗?为什么?轴线角:如果角的终边落在坐标轴上,就说该角不属于任何象限,习惯上称其为轴线角.思考:锐角与第一象限的角是什么关系?
钝角与第二象限的角是什么关系?
直角与轴线角是什么关系?锐角一定是第一象限的角,第一象限角不一定是锐角.钝角一定是第二象限的角,第二象限角不一定是钝角.直角一定是轴线角,轴线角不一定是直角.思考:第二象限的角一定比第一象限的角大吗? 象限角只能反映角的终边所在象限,不能反映角的大小. 思考:一个角的角度一旦确定,其终边位置可否确定?思考:一个角的终边确定,其角度可否确定下来?1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A,B,C的关系是( )
A.B=A∩C B.B∪C=C
C.A?C D.A=B=CB全优83页限时规范训练4.若α是第四象限的角,则180°-α是第______象限的角.三【解析】∵α是第四象限的角,∴-α是第一象限角, 则由任意角的定义知,180°-α是第三象限角.【例】 在坐标系中画出下列各角,观察它们的终边具有什么关系?任意两角的关系是什么呢?
-32°,328°,-392°-32°-392°o328°解答:各角的终边相同思考:它们的终边具有什么关系呢?思考:终边相同的角间具有什么关系呢? 如何表示与∠α终边相同的角呢?-32°,328°,-392°思考:所有与-32°角终边相同的角,连同-32°
角在内,可构成一个集合S,你能用描述
法表示集合S吗? 终边相同的角所有与 终边相同的角,连同 在内都可以写成 (k 是整数)的形式 . 终边相同的二角相差360度的整数倍练习:课本5页 2所以与 角终边相同的角是 ,它是第二象限角.练习:课本5页 4(2)(3)7.已知角α=-1 000°,则与α终边相同的最小正角是________.80°【解析】∵-1 000°=-3×360°+80°,∴80°与-1 000°终边相同.又终边相同的两个角相差360°的整数倍,∴在[0°,360°)上,只有80°与-1 000°终边相同,∴与-1 000°终边相同的最小正角是80°.全优第3页能力提高5.如果θ为小于360°的正角且这个角θ的4倍角即4θ与这个角的终边重合,求θ的值.【解析】由题意得4θ=θ+k×360°(k∈Z),即θ=k×120°,而θ为小于360°的正角,所以θ的值为120°或240°.全优83页限时规范训练例2 写出终边在y轴上的角的集合。解: 0o~360o内,终边在y轴上的角有900,2700S1={β| β=900+k?3600,k∈Z} ={β| β= 900+(2k)?1800, k∈Z}S2={β| β=2700+k?3600,k∈Z}={β| β= 900+1800+2k?1800, k∈Z}={β| β= 900+(2k+1)1800 ,k∈Z}S=S1∪S2={β|β=900+k?1800 ,k∈Z}所以, 终边在y轴上的角的集合:例题补充:终边在x轴上的角的集合?例2:写出终边在Y轴上的角的集合:思路一:分正负半轴两种情况分析。思路二:Y轴可以看成是X轴按逆时针
旋转90°得到。终边在坐标轴上角的取值0090018002700 +K*3600+K*3600+K*3600+K*3600或3600+K*3600思考:如何表示象限角?象限角的表示:解:终边在射线 y = x 正方向上的角的集合是
A={ }终边在终边在射线 y= x负方向上的角的集合是
B={ }所以终边在y=x上的角的集合是S中适合 的元素是
45°-2×180°= -315° 45°-1×180°= -135°
45°+0×180°= 45° 45°+1×180°= 225°
45°+2×180°= 405° 45°+3×180°= 585°练习:课本5页 5(2)2.写出与角60°的终边在一条直线上的角的集合.【解析】在0°~360°内,与角60°的终边在一条直线上的角是60°与240°. 故与角60°的终边在一条直线上的角的集合是S={α|α=k×360°+60°,k∈Z}∪{α|α=k×360°+240°,k∈Z} ={α|α=2k×180°+60°,k∈Z}∪{α|α=2k×180°+180°+60°,k∈Z}={α|α=2k×180°+60°,k∈Z}∪{α|α=(2k+1)×180°+60°,k∈Z}={α|α=n×180°+60°,n∈Z}.全优第2页变式训练y=xS={β|β=450+k?1800 ,k∈Z}练习: 写出终边在如图位置的角的集合:练习:课本10页 5(2)2.下列表示中不正确的是( )
A.终边在坐标轴上的角的集合是{α|α=k×90°,k∈Z}
B.与-50°的终边相同的角的集合是{α|α=k×360°+310°,k∈Z}
C.终边在第二、四象限的角平分线上的角的集合是{α|α=k×360°-45°,k∈Z}
D.终边在直线y=x上的角的集合是{α|α=k×180°+45°,k∈Z}C全优83页限时规范训练3.如图所示的阴影部分是45°角(终边为OA)与300°角(终边为OB)的终边所夹的区域,试写出阴影区域内的角的集合(虚线表示不含边界).【解析】阴影区域内的角的集合是
S={α|k×360°-60°≤α≤k×360°+45°,k∈Z}.全优第3页变式训练
