1.1.2 弧度制课件
图片预览







文档简介
课件28张PPT。长度可以用米、厘米、英尺、码等不同的单位度量.
物体的重量可以用千克、磅等不同的单位度量.
不同的单位制能给解决问题带来方便,以度为单位度量角的大小是一种常用方法,为了进一步研究的需要,我们还需建立一个度量角的单位制. 角度制用“度”作单位来度量角的单位制称作 “角度制”.思考:在平面几何中,1°的角是怎样定义的? 将圆周分成360等份,每一段圆弧所对的圆心角就是1°的角. 角度制的单位有:度、分 在角度制下,当把两个带着度、分、秒为单位的角相加、相减时,由于运算进率不是十进制,总给我们带来不少困难.角度制弧度制1.1.2 弧度制 用弧度做单位来度量角的单位制叫做 弧度制. zxxk
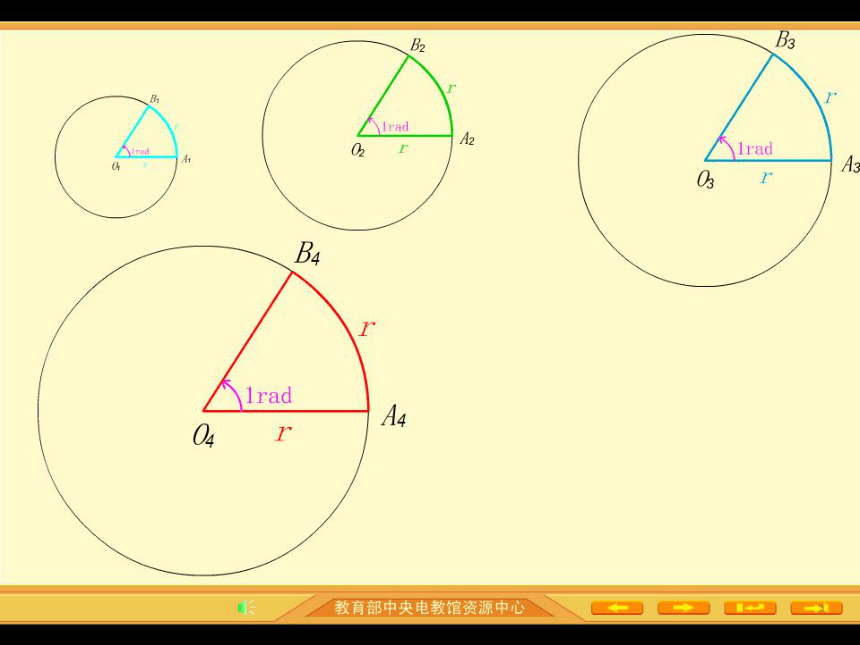
弧度制单位:弧度(或rad) 把长度等于半径长的圆弧所对的圆心角叫做1弧度的角。我们把长度等于半径长的弧所对的圆心角叫做1弧度的角。弧度制用符号rad表示,读作弧度。弧度制的单位rad可以省略不写,如:1 rad可以写成1约定: 正角的弧度数为正数,
负角的弧度数为负数,
零角的弧度数为0.思考:我们知道,在角度制里,角的大小与半径大小无关,那在弧度制里,角的大小是否与半径有关呢?如果半径为r的圆的圆心角a所对弧的长为l,那么,角a的弧度数的绝对值是
练习:课本9页 6思考:一个圆到底是多少弧度呢?为什么?解:∵一个圆对应的弧长为2πr,
∴其对应的圆心角的弧度说为:∵一个圆的度数是360°,
∴360°=2π,即:
π=180°π=180°1°=( ) rad
∵180°=π
∴1 rad=( )°
∵π=180°
∴
再次思考:弧度的大小是否与半径有关?完成课本P 6 探究的表格18003600逆时针57.30顺时针-114.60πr顺时针-18000未作旋转00πr逆时针2πr逆时针角度制与弧度制的互换:一些特殊角的弧度数:(课本8页)
角度
弧度
①、弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度; ②、1弧度是等于半径长的圆弧所对的圆心角的大小,而 是圆的 所对的圆心角的大小;
③、不论是以“弧度”还是以“度”为单位的角的大小都是一个与半径大小无关的定值.Z、xxk
角度制与弧度制的比较例题讲解例1(1)把67°30′化成弧度制。
(2)把 化成角度制。解(1)∵67°30′=67.5°= ,
又∵1°=
∴67°30′=67.5 =
(2) = 180°=405°P9 1【例1】 (1)将下列各角度化成弧度:①-2 220°;②765°.【解析】① -2 220°=②765°=全优第4页典例剖析P9 2练习3:用弧度表示:
(1)终边在x轴上的角的集合;
(2)终边在y轴上的角的集合。【例2】 (1)把-1 500°角化成2kπ+α(0≤α<2π,k∈Z)的形式;
(2)若β∈[-4π,0]且β与(1)中的角α的终边相同,求β.【解析】(1)因为-1 500°=-1 800°+300°所以全优5页典例剖析【例2】 (1)把-1 500°角化成2kπ+α(0≤α<2π,k∈Z)的形式;
(2)若β∈[-4π,0]且β与(1)中的角α的终边相同,求β.(2)因为β与角α的终边相同,所以而β∈[-4π,0],【解析】由题意,知∴当k=-3时,当k=-4时,全优第6页基础夯实例3.利用弧度制证明下列关于扇形的公式: 全优6页基础夯实DA.2°B.2C.4°D.4全优6页基础夯实6.直径为10 cm的滑轮上有一条长为6 cm的弦,P是此弦的中点,若滑轮以每秒5弧度的角速度旋转,则经过5秒钟后,点P转过的弧长等于________.【解析】如图,连接OP且延长到圆点A.∵CD=6 cm,OD=5 cm,∴OP=4 cm.∵A,P两点角速度相同,∴5秒后P点转过的角度为25弧度.∴点P转过的弧长为25×4=100(cm).全优第6页能力提高
物体的重量可以用千克、磅等不同的单位度量.
不同的单位制能给解决问题带来方便,以度为单位度量角的大小是一种常用方法,为了进一步研究的需要,我们还需建立一个度量角的单位制. 角度制用“度”作单位来度量角的单位制称作 “角度制”.思考:在平面几何中,1°的角是怎样定义的? 将圆周分成360等份,每一段圆弧所对的圆心角就是1°的角. 角度制的单位有:度、分 在角度制下,当把两个带着度、分、秒为单位的角相加、相减时,由于运算进率不是十进制,总给我们带来不少困难.角度制弧度制1.1.2 弧度制 用弧度做单位来度量角的单位制叫做 弧度制. zxxk
弧度制单位:弧度(或rad) 把长度等于半径长的圆弧所对的圆心角叫做1弧度的角。我们把长度等于半径长的弧所对的圆心角叫做1弧度的角。弧度制用符号rad表示,读作弧度。弧度制的单位rad可以省略不写,如:1 rad可以写成1约定: 正角的弧度数为正数,
负角的弧度数为负数,
零角的弧度数为0.思考:我们知道,在角度制里,角的大小与半径大小无关,那在弧度制里,角的大小是否与半径有关呢?如果半径为r的圆的圆心角a所对弧的长为l,那么,角a的弧度数的绝对值是
练习:课本9页 6思考:一个圆到底是多少弧度呢?为什么?解:∵一个圆对应的弧长为2πr,
∴其对应的圆心角的弧度说为:∵一个圆的度数是360°,
∴360°=2π,即:
π=180°π=180°1°=( ) rad
∵180°=π
∴1 rad=( )°
∵π=180°
∴
再次思考:弧度的大小是否与半径有关?完成课本P 6 探究的表格18003600逆时针57.30顺时针-114.60πr顺时针-18000未作旋转00πr逆时针2πr逆时针角度制与弧度制的互换:一些特殊角的弧度数:(课本8页)
角度
弧度
①、弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度; ②、1弧度是等于半径长的圆弧所对的圆心角的大小,而 是圆的 所对的圆心角的大小;
③、不论是以“弧度”还是以“度”为单位的角的大小都是一个与半径大小无关的定值.Z、xxk
角度制与弧度制的比较例题讲解例1(1)把67°30′化成弧度制。
(2)把 化成角度制。解(1)∵67°30′=67.5°= ,
又∵1°=
∴67°30′=67.5 =
(2) = 180°=405°P9 1【例1】 (1)将下列各角度化成弧度:①-2 220°;②765°.【解析】① -2 220°=②765°=全优第4页典例剖析P9 2练习3:用弧度表示:
(1)终边在x轴上的角的集合;
(2)终边在y轴上的角的集合。【例2】 (1)把-1 500°角化成2kπ+α(0≤α<2π,k∈Z)的形式;
(2)若β∈[-4π,0]且β与(1)中的角α的终边相同,求β.【解析】(1)因为-1 500°=-1 800°+300°所以全优5页典例剖析【例2】 (1)把-1 500°角化成2kπ+α(0≤α<2π,k∈Z)的形式;
(2)若β∈[-4π,0]且β与(1)中的角α的终边相同,求β.(2)因为β与角α的终边相同,所以而β∈[-4π,0],【解析】由题意,知∴当k=-3时,当k=-4时,全优第6页基础夯实例3.利用弧度制证明下列关于扇形的公式: 全优6页基础夯实DA.2°B.2C.4°D.4全优6页基础夯实6.直径为10 cm的滑轮上有一条长为6 cm的弦,P是此弦的中点,若滑轮以每秒5弧度的角速度旋转,则经过5秒钟后,点P转过的弧长等于________.【解析】如图,连接OP且延长到圆点A.∵CD=6 cm,OD=5 cm,∴OP=4 cm.∵A,P两点角速度相同,∴5秒后P点转过的角度为25弧度.∴点P转过的弧长为25×4=100(cm).全优第6页能力提高
