18.1.1 平行四边形的性质(第1课时 平行四边形的边、角特征)课件(共21张PPT)-2023-2024学年人教版初中数学八年级下册
文档属性
| 名称 | 18.1.1 平行四边形的性质(第1课时 平行四边形的边、角特征)课件(共21张PPT)-2023-2024学年人教版初中数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
18.1.1 平行四边形的性质
第十八章 平行四边形
第1课时 平行四边形的边、角特征
观察下列图片,你能抽象出什么几何图形?
情境引入
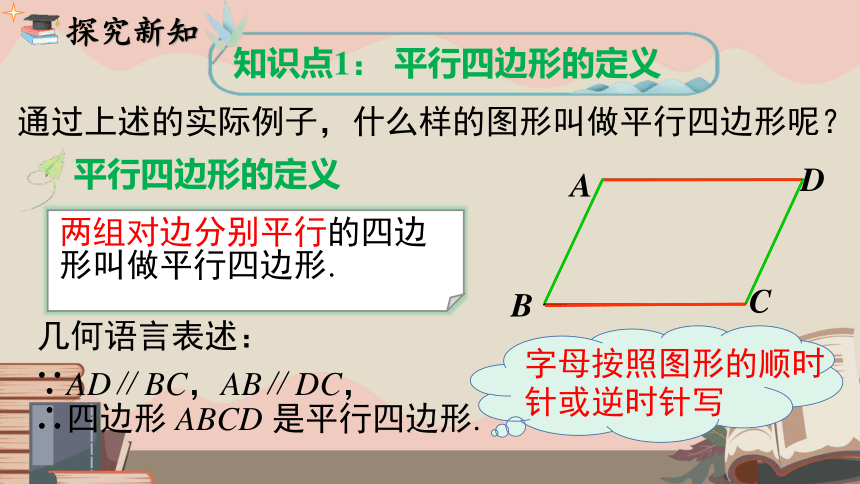
知识点1: 平行四边形的定义
探究新知
通过上述的实际例子,什么样的图形叫做平行四边形呢?
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
A
B
D
C
几何语言表述:
∵AD∥BC,AB∥DC,
∴四边形 ABCD 是平行四边形.
字母按照图形的顺时针或逆时针写
符号:□
记作:□ABCD
读作:平行四边形ABCD
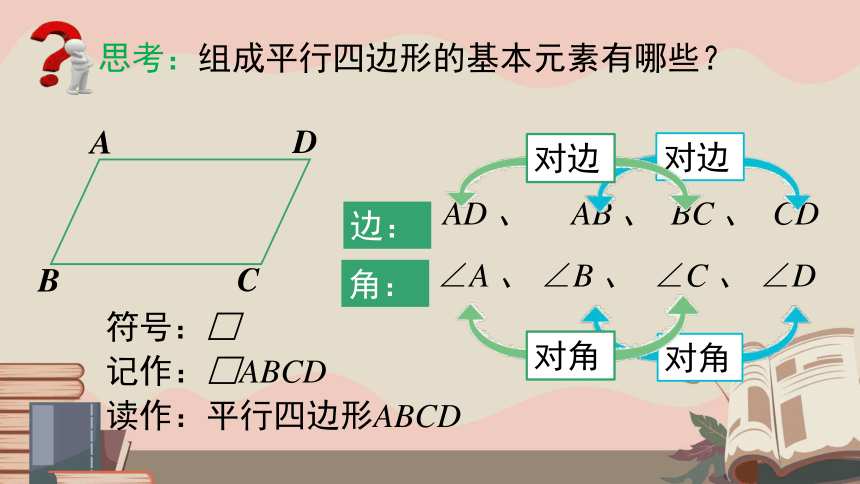
思考:组成平行四边形的基本元素有哪些?
A
B
D
C
边:
角:
AD 、 AB 、 BC 、 CD
∠A 、 ∠B 、 ∠C 、 ∠D
对边
对边
对角
对角
两组对边分别平行
思考:平行四边形和四边形的联系是什么?
一个“四边形”必须具备“两组对边分别平行”才是平行四边形;反之,平行四边形一定是“两组对边分别平行”的“四边形”
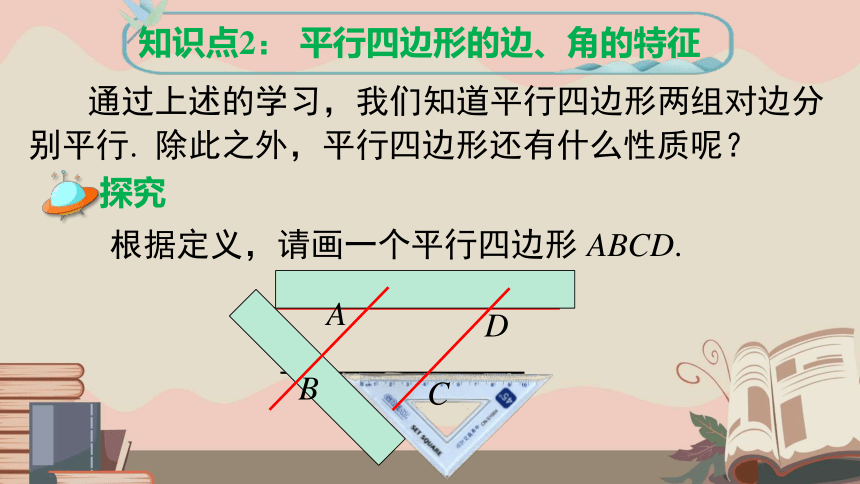
知识点2: 平行四边形的边、角的特征
通过上述的学习,我们知道平行四边形两组对边分别平行. 除此之外,平行四边形还有什么性质呢?
根据定义,请画一个平行四边形 ABCD.
探究
D
A
B
C
A
B
C
D
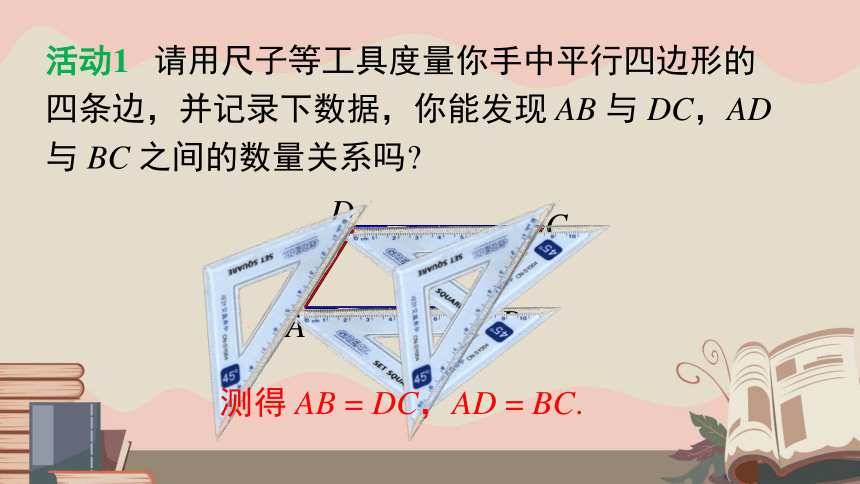
活动1 请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现 AB 与 DC,AD 与 BC 之间的数量关系吗
测得 AB = DC,AD = BC.
A
B
C
D
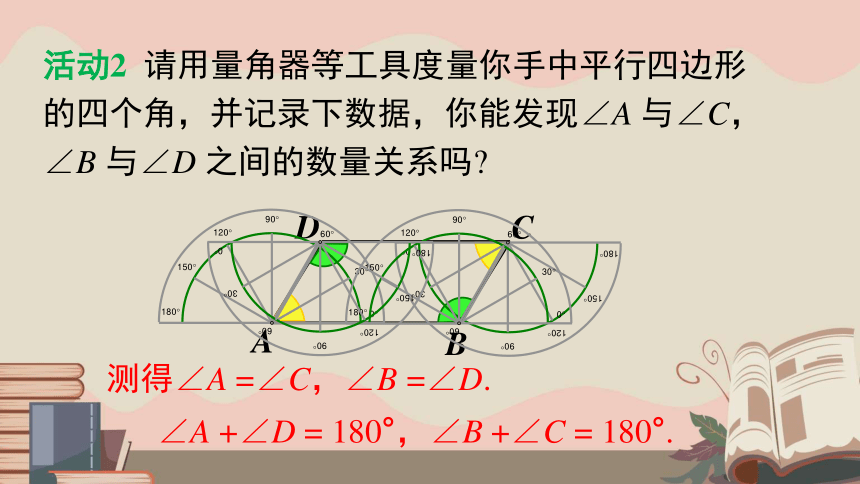
测得∠A =∠C,∠B =∠D.
活动2 请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A 与∠C,∠B 与∠D 之间的数量关系吗
∠A +∠D = 180°,∠B +∠C = 180°.
A
B
C
D
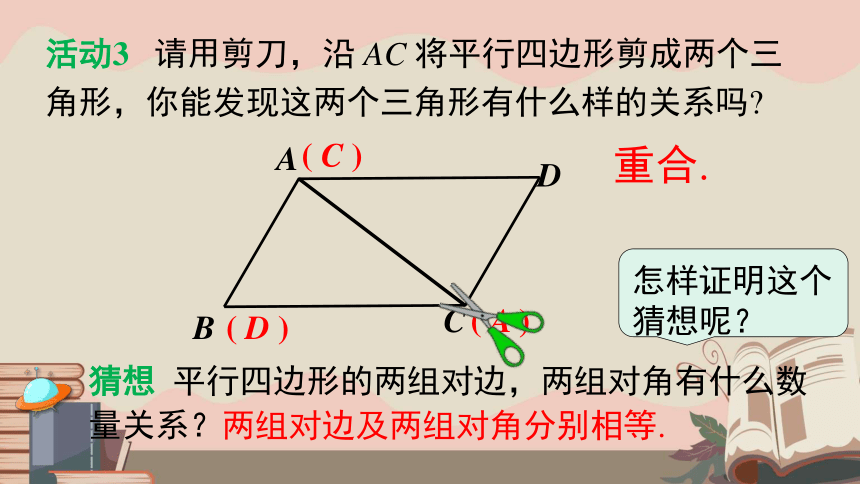
活动3 请用剪刀,沿 AC 将平行四边形剪成两个三角形,你能发现这两个三角形有什么样的关系吗
( C )
( A )
( D )
猜想 平行四边形的两组对边,两组对角有什么数量关系?
两组对边及两组对角分别相等.
怎样证明这个猜想呢?
重合.
已知:四边形 ABCD 是平行四边形.
求证:AD = BC,AB = CD,
∠BAD = ∠BCD,∠ABC = ∠ADC.
A
B
C
D
1
4
3
2
证一证
分析:
求证 AD = BC,AB = CD
AD∥BC,AB∥CD
连接 AC
全等
AC 是公共边
AD = BC,AB = CD,
∠ABC =∠ADC
△ABC≌△CDA
∠BAD = ∠BCD
逆向思维
∠1 =∠2,∠3 =∠4
思考:不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?
A
B
C
D
分析:
AD∥BC,AB∥CD
∠A +∠B = 180°,
∠A +∠D = 180°
∠B = ∠D
同理可得
∠A =∠C
正向思维
归纳总结
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的性质
几何语言表述:
∵ 四边形 ABCD 是平行四边形,
∴ AB = CD,AD = BC,
∠A =∠C,∠B = ∠D
A
B
C
D
典例精析
例1 如图,在 □ABCD 中,DE⊥AB,BF⊥CD,垂足分别是 E,F.
求证:AE = CF.
D
A
B
C
F
E
分析:
正向思维
□ABCD
AD = BC,∠A =∠C
DE⊥AB,BF⊥CD
∠DEA =∠BFC
逆向思维
求证 AE = CF
全等
△DEA≌△BFC
练一练
2. 如图,在□ABCD 中,BE、CF分别平分∠ABC和∠BCD,求证AF=DE.
C
D
A
B
E
F
知识点3: 平行线间的距离
追问1 如图 a∥b,c∥d ,我们能得出 AD = BC ?
a
b
c
d
D
A
B
C
总结
两条平行线之间的平行线段相等.
a
b
c
d
D
A
B
C
追问2 如图,直线 a∥b,D,C 为直线 a 上任意两点,点 D 到直线 b 的距离和点 C 到直线b 的距离相等吗?
F
E
总结
如果有两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离.
思考:两条平行线之间的距离和点与点之间的距离、点到直线的距离有何联系与区别?
C
a
b
D
A
B
F
E
总结
任何两条平行线之间的距离都是存在的、唯一的,都是夹在这两条平行线间最短的线段长度.
点与点之间的距离是定义点到直线的距离、两条平行线之间的距离的基础,它们本质都是点与点之间的距离.
3. 在同一平面上,直线 a,b,c 是三条平行直线.
如果直线 a 和 b 的距离为 7,直线 b 和 c 的距离为 3,
那么直线 a 和 c 的距离为 .
练一练
10 或4
C
B
A
D
E
F
当堂小结
平行
四边形
定义
_________________的四边形
性质
平行四边形的____________________
两条平行线之间的任何两条平行线段都____
平行四边形的___________________
两组对边分别平行
两组对边分别平行相等
边
角
两条平行线间的距离:一条直线上___________到另一条直线的距离
综合应用
两组对角分别相等
任意一点
相等
感谢您的观看
一切为了学生,为了一切学生,为了学生一切!
18.1.1 平行四边形的性质
第十八章 平行四边形
第1课时 平行四边形的边、角特征
观察下列图片,你能抽象出什么几何图形?
情境引入
知识点1: 平行四边形的定义
探究新知
通过上述的实际例子,什么样的图形叫做平行四边形呢?
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
A
B
D
C
几何语言表述:
∵AD∥BC,AB∥DC,
∴四边形 ABCD 是平行四边形.
字母按照图形的顺时针或逆时针写
符号:□
记作:□ABCD
读作:平行四边形ABCD
思考:组成平行四边形的基本元素有哪些?
A
B
D
C
边:
角:
AD 、 AB 、 BC 、 CD
∠A 、 ∠B 、 ∠C 、 ∠D
对边
对边
对角
对角
两组对边分别平行
思考:平行四边形和四边形的联系是什么?
一个“四边形”必须具备“两组对边分别平行”才是平行四边形;反之,平行四边形一定是“两组对边分别平行”的“四边形”
知识点2: 平行四边形的边、角的特征
通过上述的学习,我们知道平行四边形两组对边分别平行. 除此之外,平行四边形还有什么性质呢?
根据定义,请画一个平行四边形 ABCD.
探究
D
A
B
C
A
B
C
D
活动1 请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现 AB 与 DC,AD 与 BC 之间的数量关系吗
测得 AB = DC,AD = BC.
A
B
C
D
测得∠A =∠C,∠B =∠D.
活动2 请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A 与∠C,∠B 与∠D 之间的数量关系吗
∠A +∠D = 180°,∠B +∠C = 180°.
A
B
C
D
活动3 请用剪刀,沿 AC 将平行四边形剪成两个三角形,你能发现这两个三角形有什么样的关系吗
( C )
( A )
( D )
猜想 平行四边形的两组对边,两组对角有什么数量关系?
两组对边及两组对角分别相等.
怎样证明这个猜想呢?
重合.
已知:四边形 ABCD 是平行四边形.
求证:AD = BC,AB = CD,
∠BAD = ∠BCD,∠ABC = ∠ADC.
A
B
C
D
1
4
3
2
证一证
分析:
求证 AD = BC,AB = CD
AD∥BC,AB∥CD
连接 AC
全等
AC 是公共边
AD = BC,AB = CD,
∠ABC =∠ADC
△ABC≌△CDA
∠BAD = ∠BCD
逆向思维
∠1 =∠2,∠3 =∠4
思考:不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?
A
B
C
D
分析:
AD∥BC,AB∥CD
∠A +∠B = 180°,
∠A +∠D = 180°
∠B = ∠D
同理可得
∠A =∠C
正向思维
归纳总结
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的性质
几何语言表述:
∵ 四边形 ABCD 是平行四边形,
∴ AB = CD,AD = BC,
∠A =∠C,∠B = ∠D
A
B
C
D
典例精析
例1 如图,在 □ABCD 中,DE⊥AB,BF⊥CD,垂足分别是 E,F.
求证:AE = CF.
D
A
B
C
F
E
分析:
正向思维
□ABCD
AD = BC,∠A =∠C
DE⊥AB,BF⊥CD
∠DEA =∠BFC
逆向思维
求证 AE = CF
全等
△DEA≌△BFC
练一练
2. 如图,在□ABCD 中,BE、CF分别平分∠ABC和∠BCD,求证AF=DE.
C
D
A
B
E
F
知识点3: 平行线间的距离
追问1 如图 a∥b,c∥d ,我们能得出 AD = BC ?
a
b
c
d
D
A
B
C
总结
两条平行线之间的平行线段相等.
a
b
c
d
D
A
B
C
追问2 如图,直线 a∥b,D,C 为直线 a 上任意两点,点 D 到直线 b 的距离和点 C 到直线b 的距离相等吗?
F
E
总结
如果有两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离.
思考:两条平行线之间的距离和点与点之间的距离、点到直线的距离有何联系与区别?
C
a
b
D
A
B
F
E
总结
任何两条平行线之间的距离都是存在的、唯一的,都是夹在这两条平行线间最短的线段长度.
点与点之间的距离是定义点到直线的距离、两条平行线之间的距离的基础,它们本质都是点与点之间的距离.
3. 在同一平面上,直线 a,b,c 是三条平行直线.
如果直线 a 和 b 的距离为 7,直线 b 和 c 的距离为 3,
那么直线 a 和 c 的距离为 .
练一练
10 或4
C
B
A
D
E
F
当堂小结
平行
四边形
定义
_________________的四边形
性质
平行四边形的____________________
两条平行线之间的任何两条平行线段都____
平行四边形的___________________
两组对边分别平行
两组对边分别平行相等
边
角
两条平行线间的距离:一条直线上___________到另一条直线的距离
综合应用
两组对角分别相等
任意一点
相等
感谢您的观看
一切为了学生,为了一切学生,为了学生一切!
