18.2.1 矩形 第一课时 课件(共23张PPT)2023-2024学年人教版初中数学八年级下册
文档属性
| 名称 | 18.2.1 矩形 第一课时 课件(共23张PPT)2023-2024学年人教版初中数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-19 21:22:25 | ||
图片预览




文档简介
(共23张PPT)
18.2 特殊的平行四边形
18.2.1 矩形(第一课时)
形
边
四
形
平
人教版初中数学八年级下册
一、情境导入
想一想,这里面应用了平行四边形的什么性质?
一、情境引入
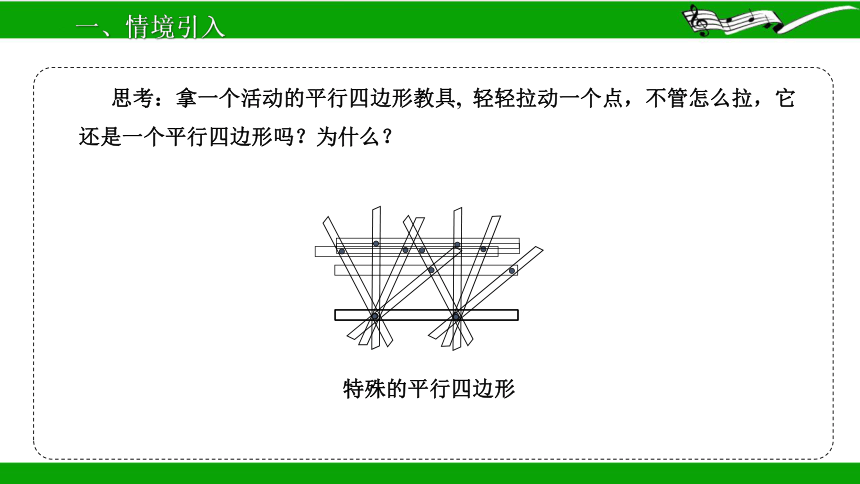
思考:拿一个活动的平行四边形教具, 轻轻拉动一个点,不管怎么拉,它还是一个平行四边形吗?为什么?
特殊的平行四边形
你能给这个图形下一个定义吗?
C
B
A
D
有一个角是直角的平行四边形叫做矩形, 也就是长方形.
概念
矩形
长方形
二、合作探究
矩形也是常见的图形, 能否举出生活中矩形形象的例子?
二、合作探究
四边形
平行四边形
矩形
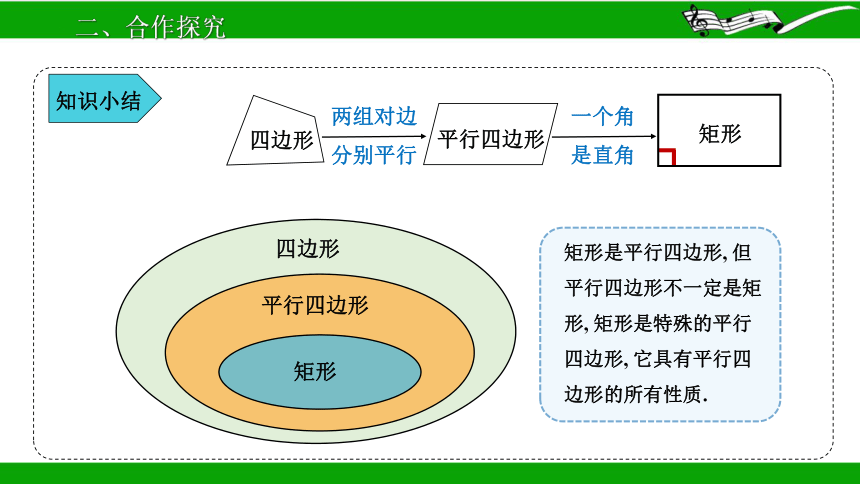
两组对边分别平行
一个角是直角
四边形
平行四边形
矩形
知识小结
二、合作探究
矩形是平行四边形, 但平行四边形不一定是矩形, 矩形是特殊的平行四边形, 它具有平行四边形的所有性质.
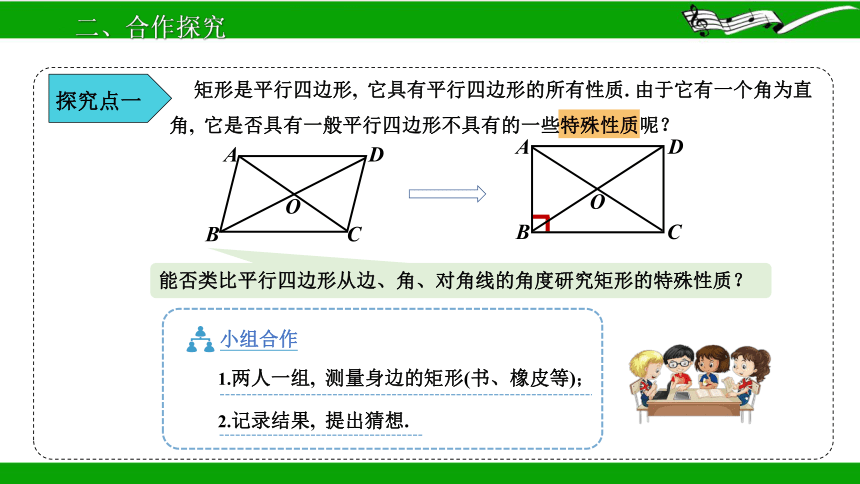
矩形是平行四边形, 它具有平行四边形的所有性质. 由于它有一个角为直角, 它是否具有一般平行四边形不具有的一些特殊性质呢?
A
B
C
D
O
C
B
A
D
O
能否类比平行四边形从边、角、对角线的角度研究矩形的特殊性质?
小组合作
1.两人一组, 测量身边的矩形(书、橡皮等);
2.记录结果, 提出猜想.
探究点一
二、合作探究
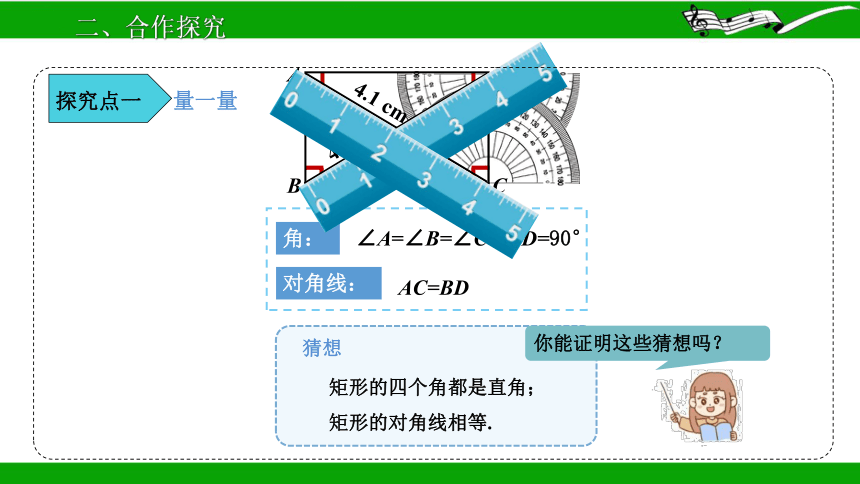
AC=BD
对角线:
角:
∠A=∠B=∠C=∠D=90°
C
B
A
D
O
4.1 cm
4.1 cm
矩形的四个角都是直角;
矩形的对角线相等.
你能证明这些猜想吗?
量一量
猜想
c
二、合作探究
探究点一
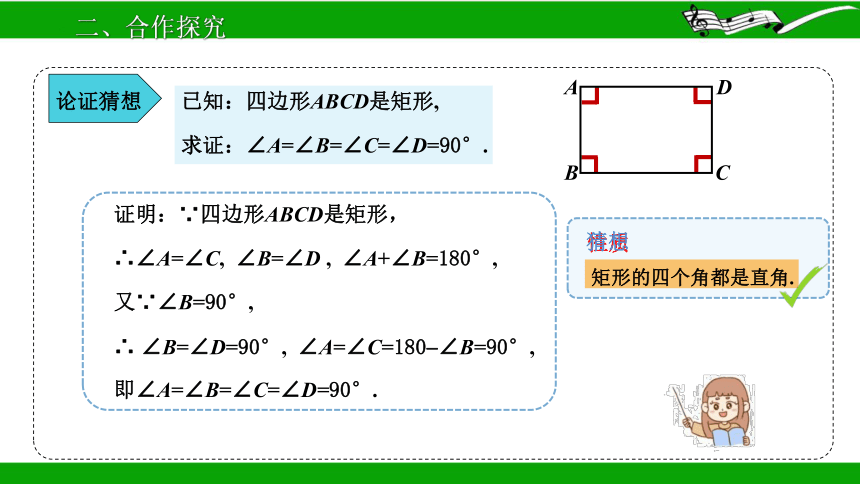
已知:四边形ABCD是矩形,
求证:∠A=∠B=∠C=∠D=90°.
矩形的四个角都是直角.
证明:∵四边形ABCD是矩形,
∴∠A=∠C, ∠B=∠D , ∠A+∠B=180°,
又∵∠B=90°,
∴ ∠B=∠D=90°, ∠A=∠C=180 ∠B=90°,
即∠A=∠B=∠C=∠D=90°.
C
B
A
D
论证猜想
性质
猜想
二、合作探究
已知:如图, 矩形ABCD的对角线AC、BD相交于点O, ∠ABC=90°.
求证:AC=BD.
矩形的对角线相等.
证明:∵四边形ABCD是矩形,
∴AB=DC, ∠ABC=∠DCB=90°,
在△ABC和△DCB中,
AB=DC
∠ABC=∠DCB
BC=CB
C
B
A
D
O
∴△ABC≌△DCB(SAS).
∴AC=DB.
论证猜想
性质
猜想
二、合作探究
总结归纳
图形 性质 几何语言
C
B
A
D
O
矩形的对边平行且相等
矩形的四个角都是直角
矩形的对角线相等且互相平分
矩形是轴对称图形且有两条对称轴
∵ 四边形ABCD是矩形
∴ AB CD , AD BC
∵ 四边形ABCD是矩形
∴ ∠DAB=∠ABC=…=90°
∵ 四边形ABCD是矩形
∴ AC=BD, OA=OB=OC=OD
矩形边的性质
矩形角的性质
矩形对角线的性质
矩形的对称性质
二、合作探究
如图,矩形ABCD的对角线AC, BD相交于点O. 我们观察Rt△ABC, 在Rt△ABC中, BO是斜边AC上的中线, BO与AC有什么关系?
C
B
A
D
O
四边形ABCD是矩形
矩形的对角线的性质
直角三角形斜边上的中线等于斜边的一半.
直角三角形的性质
二、合作探究
探究点二
BO= BD = AC
如图, 三位学生正在做投圈游戏, 他们分别站在一个直角三角形ABC的三个顶点处, 目标物放在斜边的中点D处. 这样的队形对每个人公平吗?请说明理由.
C
B
A
D
公平.
∵在Rt△ABC中, D为斜边AC的中点,
∴ AD=CD=BD,
即三位学生到目标物的距离相等.
∴这样的队形对每个人公平.
直角三角形斜边上的中线等于斜边的一半
想一想
二、合作探究
【例题1·填一填】如图, 矩形ABCD的对角线AC, BD相交于点O.
C
B
A
D
O
典型例题
(1)图中直角三角形的个数为 .
(2)图中等腰三角形的个数为 .
(3)若AB=6, BC=8, 则AO = .
(4)若AC=10, 点E、F分别为AO、AD的中点, 则MN= .
E
F
4
4
5
2.5
三、例题精讲
【例题2·证一证】如图, 四边形ABCD是矩形, 对角线AC, BD相交于点O, BE∥AC交DC的延长线于点E. 求证:BD=BE.
典型例题
A
B
C
D
O
E
证明:∵四边形ABCD是矩形,
∴AC= BD, AB∥CE.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
三、例题精讲
【例题3·算一算】如图, 矩形ABCD的对角线AC, BD相交于点O, ∠AOB=60°, AB=4, 求矩形对角线的长.
C
B
A
D
O
60°
4
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.
∴OA=OB.
又 ∠AOB=60°,
∴△OAB是等边三角形.
∴OA=AB=4.
∴ AC=BD=2OA=8.
4
典型例题
方法小结: 如果矩形两条对角线形成的角是60°或120°, 则其中必有等边三角形 .
三、例题精讲
【例题4·算一算】如图, 将矩形ABCD沿着直线BD折叠, 使点C落在C′处, BC′交AD于点E, AD=8, AB=4, 求△BED的面积.
解:∵四边形ABCD是矩形,
∴AD∥BC, ∠A=90°,
∴∠1=∠2.
又由折叠知∠2=∠3,
∴∠1=∠3, ∴BE=DE.
设BE=DE=x,则AE=8-x.
∵在Rt△ABE中, AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得x=5, 即DE=5.
典型例题
3
2
1
∴S△BED= DE·AB= ×5×4=10.
A
B
C
D
C′
E
三、例题精讲
【例题5·算一算】如图是一张长方形纸片ABCD, 已知AB=8, AD=7, E为AB上一点, AE=5, 现要剪下一张等腰三角形纸片(△AEP ), 使点P落在长方形ABCD的某一条边上, 则等腰三角形AEP的底边长是 .
典型例题
P
P
P
三、例题精讲
四、课堂小结
1.谈谈你在这节课中学了哪些知识?
2.学到了哪些数学思想方法?
四、课堂小结
矩形的定义及性质
定义:
有一个角是直角的平行四边形叫做矩形.
矩形特有的性质:
矩形的四个角都是直角.
矩形的对角线相等.
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
1.谈谈你在这节课中学了哪些知识?
四、课堂小结
数学思想方法
2.学到了哪些数学思想方法?
从一般到特殊思想
类比思想
方程思想
分类讨论
五、课后作业
1. 基础性作业
课本第55页 第1题和第2题
2. 巩固性作业
课本第60页 第1题和第2题
3. 拓展性作业
课本第61页 第12题(1)
谢谢
THANKS
18.2 特殊的平行四边形
18.2.1 矩形(第一课时)
形
边
四
形
平
人教版初中数学八年级下册
一、情境导入
想一想,这里面应用了平行四边形的什么性质?
一、情境引入
思考:拿一个活动的平行四边形教具, 轻轻拉动一个点,不管怎么拉,它还是一个平行四边形吗?为什么?
特殊的平行四边形
你能给这个图形下一个定义吗?
C
B
A
D
有一个角是直角的平行四边形叫做矩形, 也就是长方形.
概念
矩形
长方形
二、合作探究
矩形也是常见的图形, 能否举出生活中矩形形象的例子?
二、合作探究
四边形
平行四边形
矩形
两组对边分别平行
一个角是直角
四边形
平行四边形
矩形
知识小结
二、合作探究
矩形是平行四边形, 但平行四边形不一定是矩形, 矩形是特殊的平行四边形, 它具有平行四边形的所有性质.
矩形是平行四边形, 它具有平行四边形的所有性质. 由于它有一个角为直角, 它是否具有一般平行四边形不具有的一些特殊性质呢?
A
B
C
D
O
C
B
A
D
O
能否类比平行四边形从边、角、对角线的角度研究矩形的特殊性质?
小组合作
1.两人一组, 测量身边的矩形(书、橡皮等);
2.记录结果, 提出猜想.
探究点一
二、合作探究
AC=BD
对角线:
角:
∠A=∠B=∠C=∠D=90°
C
B
A
D
O
4.1 cm
4.1 cm
矩形的四个角都是直角;
矩形的对角线相等.
你能证明这些猜想吗?
量一量
猜想
c
二、合作探究
探究点一
已知:四边形ABCD是矩形,
求证:∠A=∠B=∠C=∠D=90°.
矩形的四个角都是直角.
证明:∵四边形ABCD是矩形,
∴∠A=∠C, ∠B=∠D , ∠A+∠B=180°,
又∵∠B=90°,
∴ ∠B=∠D=90°, ∠A=∠C=180 ∠B=90°,
即∠A=∠B=∠C=∠D=90°.
C
B
A
D
论证猜想
性质
猜想
二、合作探究
已知:如图, 矩形ABCD的对角线AC、BD相交于点O, ∠ABC=90°.
求证:AC=BD.
矩形的对角线相等.
证明:∵四边形ABCD是矩形,
∴AB=DC, ∠ABC=∠DCB=90°,
在△ABC和△DCB中,
AB=DC
∠ABC=∠DCB
BC=CB
C
B
A
D
O
∴△ABC≌△DCB(SAS).
∴AC=DB.
论证猜想
性质
猜想
二、合作探究
总结归纳
图形 性质 几何语言
C
B
A
D
O
矩形的对边平行且相等
矩形的四个角都是直角
矩形的对角线相等且互相平分
矩形是轴对称图形且有两条对称轴
∵ 四边形ABCD是矩形
∴ AB CD , AD BC
∵ 四边形ABCD是矩形
∴ ∠DAB=∠ABC=…=90°
∵ 四边形ABCD是矩形
∴ AC=BD, OA=OB=OC=OD
矩形边的性质
矩形角的性质
矩形对角线的性质
矩形的对称性质
二、合作探究
如图,矩形ABCD的对角线AC, BD相交于点O. 我们观察Rt△ABC, 在Rt△ABC中, BO是斜边AC上的中线, BO与AC有什么关系?
C
B
A
D
O
四边形ABCD是矩形
矩形的对角线的性质
直角三角形斜边上的中线等于斜边的一半.
直角三角形的性质
二、合作探究
探究点二
BO= BD = AC
如图, 三位学生正在做投圈游戏, 他们分别站在一个直角三角形ABC的三个顶点处, 目标物放在斜边的中点D处. 这样的队形对每个人公平吗?请说明理由.
C
B
A
D
公平.
∵在Rt△ABC中, D为斜边AC的中点,
∴ AD=CD=BD,
即三位学生到目标物的距离相等.
∴这样的队形对每个人公平.
直角三角形斜边上的中线等于斜边的一半
想一想
二、合作探究
【例题1·填一填】如图, 矩形ABCD的对角线AC, BD相交于点O.
C
B
A
D
O
典型例题
(1)图中直角三角形的个数为 .
(2)图中等腰三角形的个数为 .
(3)若AB=6, BC=8, 则AO = .
(4)若AC=10, 点E、F分别为AO、AD的中点, 则MN= .
E
F
4
4
5
2.5
三、例题精讲
【例题2·证一证】如图, 四边形ABCD是矩形, 对角线AC, BD相交于点O, BE∥AC交DC的延长线于点E. 求证:BD=BE.
典型例题
A
B
C
D
O
E
证明:∵四边形ABCD是矩形,
∴AC= BD, AB∥CE.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
三、例题精讲
【例题3·算一算】如图, 矩形ABCD的对角线AC, BD相交于点O, ∠AOB=60°, AB=4, 求矩形对角线的长.
C
B
A
D
O
60°
4
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分.
∴OA=OB.
又 ∠AOB=60°,
∴△OAB是等边三角形.
∴OA=AB=4.
∴ AC=BD=2OA=8.
4
典型例题
方法小结: 如果矩形两条对角线形成的角是60°或120°, 则其中必有等边三角形 .
三、例题精讲
【例题4·算一算】如图, 将矩形ABCD沿着直线BD折叠, 使点C落在C′处, BC′交AD于点E, AD=8, AB=4, 求△BED的面积.
解:∵四边形ABCD是矩形,
∴AD∥BC, ∠A=90°,
∴∠1=∠2.
又由折叠知∠2=∠3,
∴∠1=∠3, ∴BE=DE.
设BE=DE=x,则AE=8-x.
∵在Rt△ABE中, AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得x=5, 即DE=5.
典型例题
3
2
1
∴S△BED= DE·AB= ×5×4=10.
A
B
C
D
C′
E
三、例题精讲
【例题5·算一算】如图是一张长方形纸片ABCD, 已知AB=8, AD=7, E为AB上一点, AE=5, 现要剪下一张等腰三角形纸片(△AEP ), 使点P落在长方形ABCD的某一条边上, 则等腰三角形AEP的底边长是 .
典型例题
P
P
P
三、例题精讲
四、课堂小结
1.谈谈你在这节课中学了哪些知识?
2.学到了哪些数学思想方法?
四、课堂小结
矩形的定义及性质
定义:
有一个角是直角的平行四边形叫做矩形.
矩形特有的性质:
矩形的四个角都是直角.
矩形的对角线相等.
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
1.谈谈你在这节课中学了哪些知识?
四、课堂小结
数学思想方法
2.学到了哪些数学思想方法?
从一般到特殊思想
类比思想
方程思想
分类讨论
五、课后作业
1. 基础性作业
课本第55页 第1题和第2题
2. 巩固性作业
课本第60页 第1题和第2题
3. 拓展性作业
课本第61页 第12题(1)
谢谢
THANKS
