数学:第十六章梯形复习课教学设计(北京课改版八年级下)
文档属性
| 名称 | 数学:第十六章梯形复习课教学设计(北京课改版八年级下) | 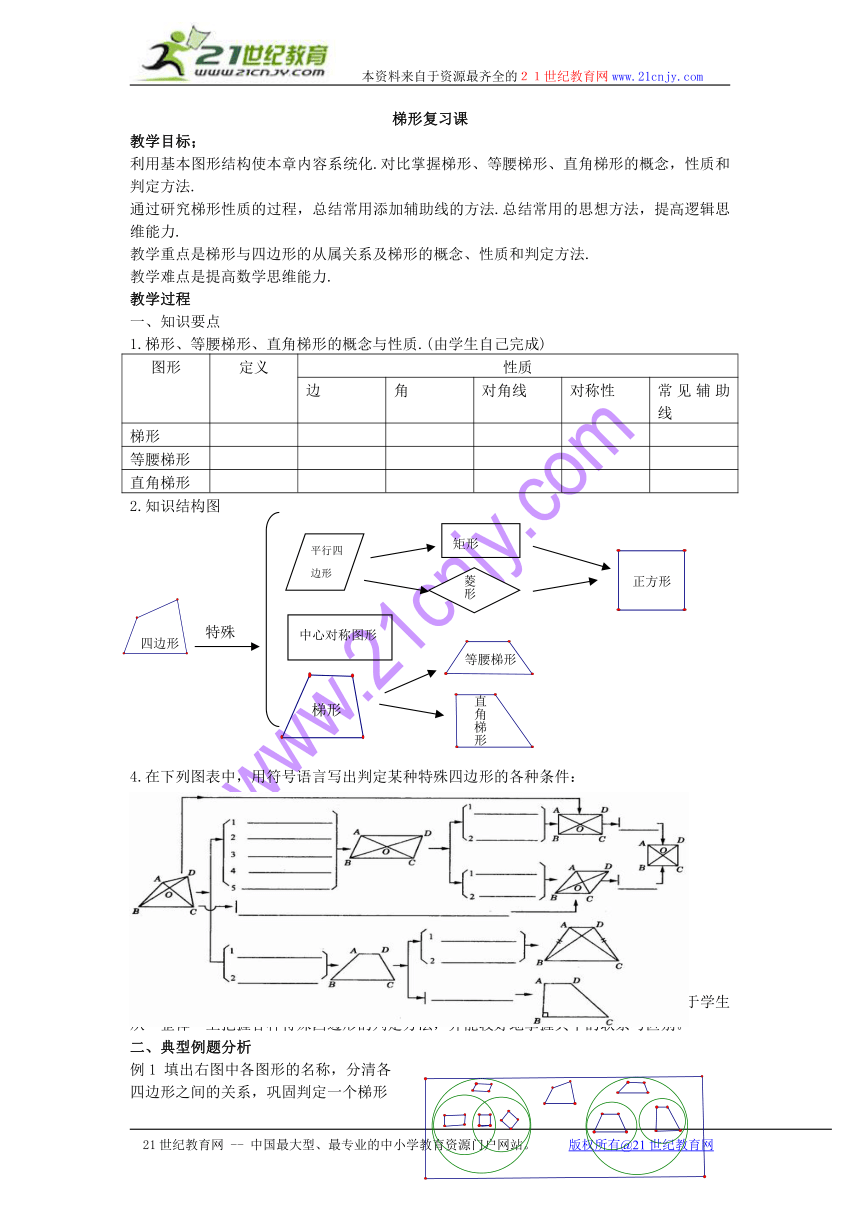 | |
| 格式 | rar | ||
| 文件大小 | 84.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-30 16:38:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
梯形复习课
教学目标;
利用基本图形结构使本章内容系统化.对比掌握梯形、等腰梯形、直角梯形的概念,性质和判定方法.
通过研究梯形性质的过程,总结常用添加辅助线的方法.总结常用的思想方法,提高逻辑思维能力.
教学重点是梯形与四边形的从属关系及梯形的概念、性质和判定方法.
教学难点是提高数学思维能力.
教学过程
一、知识要点
1.梯形、等腰梯形、直角梯形的概念与性质.(由学生自己完成)
图形 定义 性质
边 角 对角线 对称性 常见辅助线
梯形
等腰梯形
直角梯形
2.知识结构图
4.在下列图表中,用符号语言写出判定某种特殊四边形的各种条件:
说明:课前,教师可把上面的表图印发给学生,以便当堂看图填空。填写此表,有助于学生从“整体”上把握各种特殊四边形的判定方法,并能较好地掌握其中的联系与区别。
二、典型例题分析
例1 填出右图中各图形的名称,分清各
四边形之间的关系,巩固判定一个梯形
是等腰梯形的方法.
2. 等腰梯形的性质的应用,总结证明
两条线段相等的方法和添加辅助线的方法及
分析综合法的使用.
例2 已知:如图,在梯形ABCD中,AB∥CD,以AD和AC为边作ACED,DC的延长交EB于F.
求证:EF=FB.
分析:(1)分解基本图形:“ACED及对角线”,三个梯形.
(2)应用分析综合法探求解题思路,添加辅助线,将EF,
FB放在“证明两线段相等”所对应的基本图形中.
(3) 总结目前证明两条线段相等的方法,添设相应的辅助线.
特殊四边形的边、对角线的性质;
平行线间的距离相等;
过三角形一边的中点与底边平行的直线必平分第三边;
过梯形一腰的中点与底边平行的直线必平分另一腰. (补充)
说明:本题添加辅助线分为四大类.
(1) 构造三角形中位线或梯形中位线.
(延长EC交AB于G) (作EG∥DC交AD延长线于G) (联结AE) (作DG∥AC交BA延长线于G)
(2)构造全等的三角形
(3)构造等腰三角形
作FG=FB,联结EG .
(4) 构造以EB为对角线的平行四边形
3. 总结梯形中常用的辅助线,掌握化归的思想.
梯形中添加辅助线常常可以将梯形化归为三角形、平行四边形、矩形、直角梯形等.同时,还可以集中梯形中分散的已知条件,如右图中将梯形的两腰、两底角、两边之差集中到了一个三角形中.
另外还要注意:(1)从图形变换及化归角度理解梯形中
常用辅助线的作法及作用.
平移
旋转
对称
(2)其它几种作法.
一般梯形中,过上底两端点作下底的垂线;
向上延长两腰构成三角形;
例3 已知:如图,在梯形ABCD中,AB∥CD,AC┴DB,AD=BC=4,ADC=60°,E,F分别是AD,BC的中点,EF交BD于M,交AC于N.
(1) 求EF、MN的长及S梯形ABCD;
(2)观察MN的长与梯形上、下底的关系,
并思考结论能否推广到一般梯形?
分析:本题可采用(1)(2)中辅助线的作法,
解得EF=2,MN=2,S梯形ABCD=12,
MN=
三、师生共同小结
1.基本方法.
(1)利用基本图形结构使知识系统化;
(2)证明两条线段相等的方法及和差关系的方法,两线垂直、平行的方法.
(3)利用变换的思想添加辅助线的方法.
(4)探究解题思路时的分析、综合法.
2.基本思想及观点:
(1)“特殊---一般---特殊”认识事物的方法;
(2)化归的思想;
四、作业
板书设计:
矩形
特殊
平行四
边形
菱形
正方形
四边形
梯形
等腰梯形
直角梯形
中心对称图形
作FG∥CA
作EG┴DF,BH┴DF
作FG∥DA
(1)
(2)
例2已知:如图,在梯形ABCD中,
AB∥CD,以AD和AC为边
作ACED,DC的延长交EB于F.
求证:EF=FB.
1.梯形、等腰梯形、直角梯形的概念与性质.
图形 定义 性质
边 角 对角线 对称性 常见辅助线
梯形
等腰梯形
直角梯形
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
梯形复习课
教学目标;
利用基本图形结构使本章内容系统化.对比掌握梯形、等腰梯形、直角梯形的概念,性质和判定方法.
通过研究梯形性质的过程,总结常用添加辅助线的方法.总结常用的思想方法,提高逻辑思维能力.
教学重点是梯形与四边形的从属关系及梯形的概念、性质和判定方法.
教学难点是提高数学思维能力.
教学过程
一、知识要点
1.梯形、等腰梯形、直角梯形的概念与性质.(由学生自己完成)
图形 定义 性质
边 角 对角线 对称性 常见辅助线
梯形
等腰梯形
直角梯形
2.知识结构图
4.在下列图表中,用符号语言写出判定某种特殊四边形的各种条件:
说明:课前,教师可把上面的表图印发给学生,以便当堂看图填空。填写此表,有助于学生从“整体”上把握各种特殊四边形的判定方法,并能较好地掌握其中的联系与区别。
二、典型例题分析
例1 填出右图中各图形的名称,分清各
四边形之间的关系,巩固判定一个梯形
是等腰梯形的方法.
2. 等腰梯形的性质的应用,总结证明
两条线段相等的方法和添加辅助线的方法及
分析综合法的使用.
例2 已知:如图,在梯形ABCD中,AB∥CD,以AD和AC为边作ACED,DC的延长交EB于F.
求证:EF=FB.
分析:(1)分解基本图形:“ACED及对角线”,三个梯形.
(2)应用分析综合法探求解题思路,添加辅助线,将EF,
FB放在“证明两线段相等”所对应的基本图形中.
(3) 总结目前证明两条线段相等的方法,添设相应的辅助线.
特殊四边形的边、对角线的性质;
平行线间的距离相等;
过三角形一边的中点与底边平行的直线必平分第三边;
过梯形一腰的中点与底边平行的直线必平分另一腰. (补充)
说明:本题添加辅助线分为四大类.
(1) 构造三角形中位线或梯形中位线.
(延长EC交AB于G) (作EG∥DC交AD延长线于G) (联结AE) (作DG∥AC交BA延长线于G)
(2)构造全等的三角形
(3)构造等腰三角形
作FG=FB,联结EG .
(4) 构造以EB为对角线的平行四边形
3. 总结梯形中常用的辅助线,掌握化归的思想.
梯形中添加辅助线常常可以将梯形化归为三角形、平行四边形、矩形、直角梯形等.同时,还可以集中梯形中分散的已知条件,如右图中将梯形的两腰、两底角、两边之差集中到了一个三角形中.
另外还要注意:(1)从图形变换及化归角度理解梯形中
常用辅助线的作法及作用.
平移
旋转
对称
(2)其它几种作法.
一般梯形中,过上底两端点作下底的垂线;
向上延长两腰构成三角形;
例3 已知:如图,在梯形ABCD中,AB∥CD,AC┴DB,AD=BC=4,ADC=60°,E,F分别是AD,BC的中点,EF交BD于M,交AC于N.
(1) 求EF、MN的长及S梯形ABCD;
(2)观察MN的长与梯形上、下底的关系,
并思考结论能否推广到一般梯形?
分析:本题可采用(1)(2)中辅助线的作法,
解得EF=2,MN=2,S梯形ABCD=12,
MN=
三、师生共同小结
1.基本方法.
(1)利用基本图形结构使知识系统化;
(2)证明两条线段相等的方法及和差关系的方法,两线垂直、平行的方法.
(3)利用变换的思想添加辅助线的方法.
(4)探究解题思路时的分析、综合法.
2.基本思想及观点:
(1)“特殊---一般---特殊”认识事物的方法;
(2)化归的思想;
四、作业
板书设计:
矩形
特殊
平行四
边形
菱形
正方形
四边形
梯形
等腰梯形
直角梯形
中心对称图形
作FG∥CA
作EG┴DF,BH┴DF
作FG∥DA
(1)
(2)
例2已知:如图,在梯形ABCD中,
AB∥CD,以AD和AC为边
作ACED,DC的延长交EB于F.
求证:EF=FB.
1.梯形、等腰梯形、直角梯形的概念与性质.
图形 定义 性质
边 角 对角线 对称性 常见辅助线
梯形
等腰梯形
直角梯形
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
