26.1.2 反比例函数的图像与性质教案( 第1课时 ) 人教版数学九年级下册
文档属性
| 名称 | 26.1.2 反比例函数的图像与性质教案( 第1课时 ) 人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 626.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 11:09:36 | ||
图片预览

文档简介
第二十六章 反比例函数
26.1.2反比例函数的图象和性质
第一课时
教学目标
【知识与技能】 1会用描点法画反比例函数的图像。
2 理解反比例函数的性质并应用。
【过程与方法】经历实验操作,探索思考,观察分析的过程中,培养学生探究,归纳及概括的能力。
【情感与态度】在通过画图探究反比例函数图像及性质的过程中,发展学生的合作交流意识,增强求知欲望。
二、教学重难点
重点:画反比例函数图像,理解反比例函数的性质。
难点:理解反比例函数的性质,能用性质解决问题。
三、教学过程
【新课导入】
[复习导入]
我们学过的函数有哪些
一次函数解析式是什么 图像是什么?
二次函数的解析式是什么?图像是什么?
什么是反比例函数
画函数图像的步骤是什么
【新知探究】
(一)画反比例函数 和 的图象。
1.思考:①反比例函数中x的取值范围是什么?
②它的图像与坐标轴有交点吗?
③我们如何取值才能使图像更匀称?
2.画图:分组分别画出 和 的图像。
3.展示学生作品
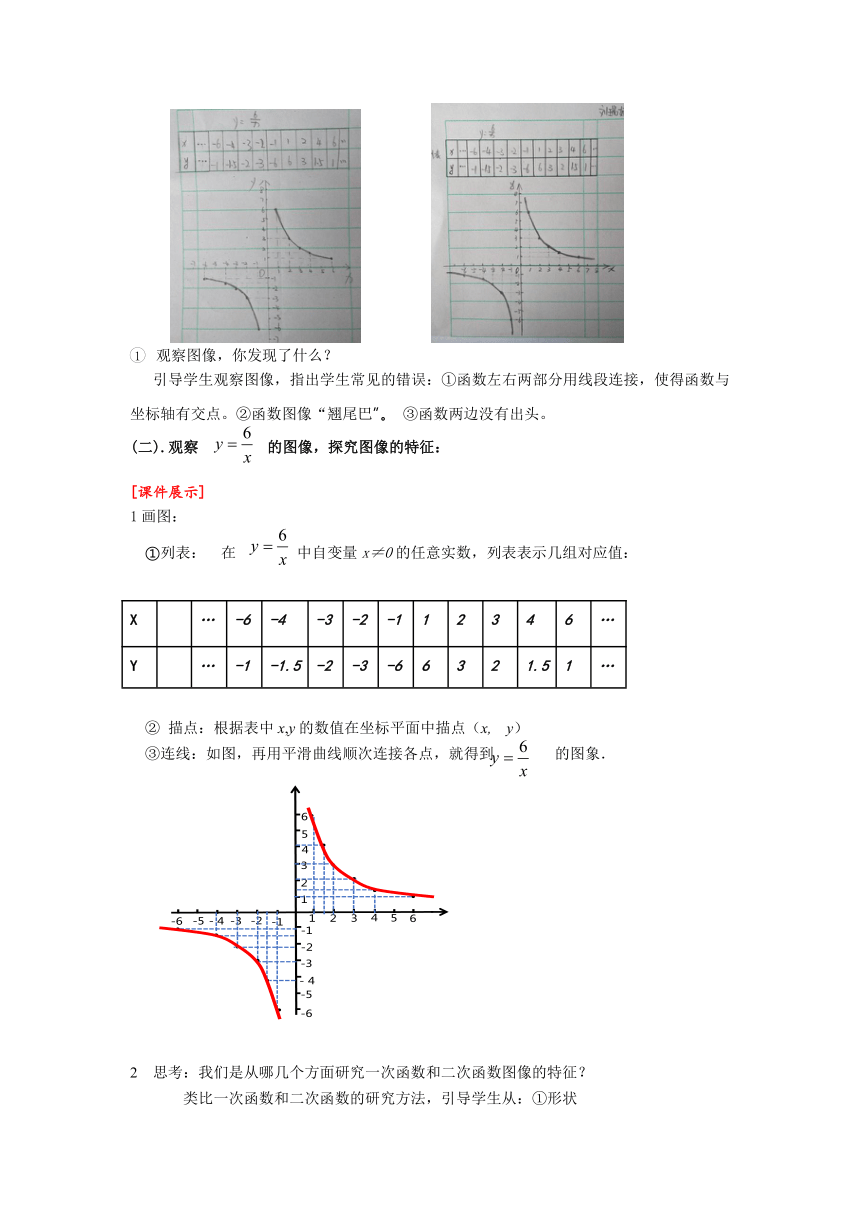
观察图像,你发现了什么?
引导学生观察图像,指出学生常见的错误:①函数左右两部分用线段连接,使得函数与坐标轴有交点。②函数图像“翘尾巴”。 ③函数两边没有出头。
(二).观察 的图像,探究图像的特征:
[课件展示]
1画图:
①列表: 在 中自变量x≠0的任意实数,列表表示几组对应值:
X … -6 -4 -3 -2 -1 1 2 3 4 6 …
Y … -1 -1.5 -2 -3 -6 6 3 2 1.5 1 …
② 描点:根据表中x,y的数值在坐标平面中描点(x, y)
③连线:如图,再用平滑曲线顺次连接各点,就得到 的图象.
2 思考:我们是从哪几个方面研究一次函数和二次函数图像的特征?
类比一次函数和二次函数的研究方法,引导学生从:①形状
②位置③增减性④对称性 进行探究反比例函数的性质。
[课件展示]
(三) 总结反比例函数图形的特征:
反比例函数解析式
形状 双曲线
位置 K>0位于一三象限 K<0位于二四象限
增减性 在每个象限内,y随x的增大而减小. 在每个象限内,y随x的 增大而增大.
对称性 都是轴对称图形(对称轴为y=x和y=-x)也是中心对称图形(对称中心为原点) .
(四) 类比k>0的分析方法探究k<0时反比例函数的特征
(五) 反比例函数性质应用
例1:如图它是反比例函数 图像的一支,根据图像,
回答下列问题:
(1)图像的另一支在第几象限?常数m的取值范围是什么?
(2)在这个函数的某一支上有两个点 A(x1,y1)和B(x2,y2)
当x1>x2时,y1与y2的大小关系是什么
(3)引伸:把第二问中的“在函数的某一支上”改为“在函数的图像上”其他条件不变,结论如何?
例2 :已知反比例函数的图像经过点A(2,6),
这个函数的图像位于哪些象限 y随x的增大如何变化
②点B(3,4) , , D(2,5)是否在这个函数的图像上
【课堂训练】
1.下列图像是反比例函数图像的是( )
2.已知反比例函数 (k为常数,k≠2)的图像位于第一
三象限,则k的取值范围是_______________
3.当x>0时, 的图像在______________象限。
4.已知反比例函数 (k为常数,且k≠1)
①若点A(1,2)在这个函数的图像上,求k的值。
②若在这个函数图像的每一支上,y随x的增大而减小,
求k的取值范围。
③若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图像上?
5.在反比例函数 的图像上有三点(x1,y1)
(x2,y2)(x3,y3),当x1>x2>0>x3时,则y1,y2,y3的大小关系是______________
【课堂小结】
1反比例函数的图像和性质
反比例函数解析式
形状 双曲线
位置 K>0位于一三象限 K<0位于二四象限
增减性 在每个象限内,y随x的增大而减小。 在每个象限内,y随x的 增大而增大。
对称性 都是轴对称图形(对称轴为y=x和y=-x)也是中心对称图形(对称中心为原点) 。
【布置作业】
书本第8页第3题和书9页第9题。
【教学反思】
在教学过程中学生通过画图直观的理解反比例函数图像的特征,类比一次函数和二次函数的研究方法,探索反比例函数的图像和性。学生更深刻的体会到数形结合的魅力。
26.1.2反比例函数的图象和性质
第一课时
教学目标
【知识与技能】 1会用描点法画反比例函数的图像。
2 理解反比例函数的性质并应用。
【过程与方法】经历实验操作,探索思考,观察分析的过程中,培养学生探究,归纳及概括的能力。
【情感与态度】在通过画图探究反比例函数图像及性质的过程中,发展学生的合作交流意识,增强求知欲望。
二、教学重难点
重点:画反比例函数图像,理解反比例函数的性质。
难点:理解反比例函数的性质,能用性质解决问题。
三、教学过程
【新课导入】
[复习导入]
我们学过的函数有哪些
一次函数解析式是什么 图像是什么?
二次函数的解析式是什么?图像是什么?
什么是反比例函数
画函数图像的步骤是什么
【新知探究】
(一)画反比例函数 和 的图象。
1.思考:①反比例函数中x的取值范围是什么?
②它的图像与坐标轴有交点吗?
③我们如何取值才能使图像更匀称?
2.画图:分组分别画出 和 的图像。
3.展示学生作品
观察图像,你发现了什么?
引导学生观察图像,指出学生常见的错误:①函数左右两部分用线段连接,使得函数与坐标轴有交点。②函数图像“翘尾巴”。 ③函数两边没有出头。
(二).观察 的图像,探究图像的特征:
[课件展示]
1画图:
①列表: 在 中自变量x≠0的任意实数,列表表示几组对应值:
X … -6 -4 -3 -2 -1 1 2 3 4 6 …
Y … -1 -1.5 -2 -3 -6 6 3 2 1.5 1 …
② 描点:根据表中x,y的数值在坐标平面中描点(x, y)
③连线:如图,再用平滑曲线顺次连接各点,就得到 的图象.
2 思考:我们是从哪几个方面研究一次函数和二次函数图像的特征?
类比一次函数和二次函数的研究方法,引导学生从:①形状
②位置③增减性④对称性 进行探究反比例函数的性质。
[课件展示]
(三) 总结反比例函数图形的特征:
反比例函数解析式
形状 双曲线
位置 K>0位于一三象限 K<0位于二四象限
增减性 在每个象限内,y随x的增大而减小. 在每个象限内,y随x的 增大而增大.
对称性 都是轴对称图形(对称轴为y=x和y=-x)也是中心对称图形(对称中心为原点) .
(四) 类比k>0的分析方法探究k<0时反比例函数的特征
(五) 反比例函数性质应用
例1:如图它是反比例函数 图像的一支,根据图像,
回答下列问题:
(1)图像的另一支在第几象限?常数m的取值范围是什么?
(2)在这个函数的某一支上有两个点 A(x1,y1)和B(x2,y2)
当x1>x2时,y1与y2的大小关系是什么
(3)引伸:把第二问中的“在函数的某一支上”改为“在函数的图像上”其他条件不变,结论如何?
例2 :已知反比例函数的图像经过点A(2,6),
这个函数的图像位于哪些象限 y随x的增大如何变化
②点B(3,4) , , D(2,5)是否在这个函数的图像上
【课堂训练】
1.下列图像是反比例函数图像的是( )
2.已知反比例函数 (k为常数,k≠2)的图像位于第一
三象限,则k的取值范围是_______________
3.当x>0时, 的图像在______________象限。
4.已知反比例函数 (k为常数,且k≠1)
①若点A(1,2)在这个函数的图像上,求k的值。
②若在这个函数图像的每一支上,y随x的增大而减小,
求k的取值范围。
③若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图像上?
5.在反比例函数 的图像上有三点(x1,y1)
(x2,y2)(x3,y3),当x1>x2>0>x3时,则y1,y2,y3的大小关系是______________
【课堂小结】
1反比例函数的图像和性质
反比例函数解析式
形状 双曲线
位置 K>0位于一三象限 K<0位于二四象限
增减性 在每个象限内,y随x的增大而减小。 在每个象限内,y随x的 增大而增大。
对称性 都是轴对称图形(对称轴为y=x和y=-x)也是中心对称图形(对称中心为原点) 。
【布置作业】
书本第8页第3题和书9页第9题。
【教学反思】
在教学过程中学生通过画图直观的理解反比例函数图像的特征,类比一次函数和二次函数的研究方法,探索反比例函数的图像和性。学生更深刻的体会到数形结合的魅力。
