5.3垂径定理同步同步辅导(含答案)
图片预览
文档简介
5.3垂径定理及其应用
一、知识梳理
1、垂径定理: 。
2、垂径定理推论: 。
二、典例精析
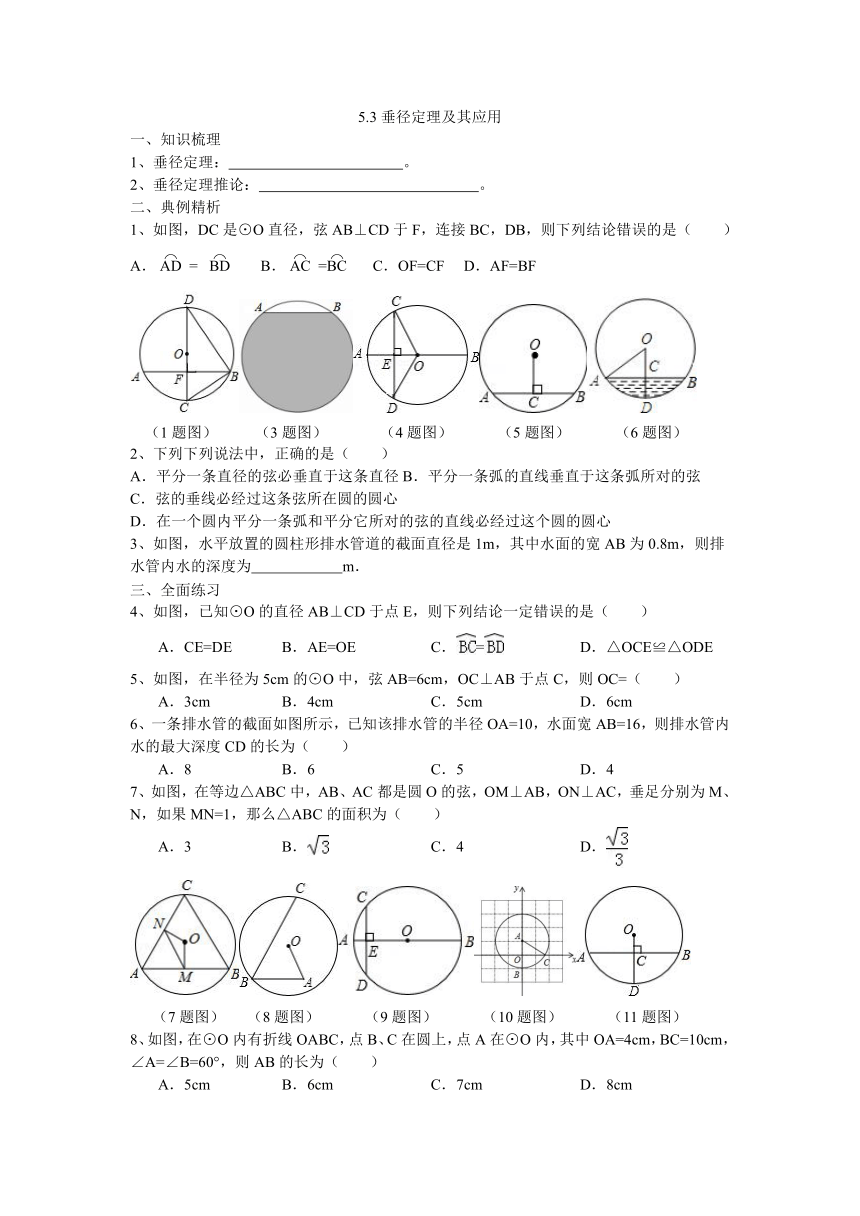
1、如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.= B.= C.OF=CF D.AF=BF
(1题图) (3题图) (4题图) (5题图) (6题图)
2、下列下列说法中,正确的是( )
A.平分一条直径的弦必垂直于这条直径B.平分一条弧的直线垂直于这条弧所对的弦
C.弦的垂线必经过这条弦所在圆的圆心
D.在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心
3、如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为 m.
三、全面练习
4、如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
A.CE=DE B. AE=OE C. = D. △OCE≌△ODE
5、如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
A.3cm B. 4cm C. 5cm D. 6cm
6、一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )
A.8 B. 6 C. 5 D. 4
7、如图,在等边△ABC中,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=1,那么△ABC的面积为( )
A.3 B. C. 4 D.
(7题图) (8题图) (9题图) (10题图) (11题图)
8、如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为( )
A.5cm B. 6cm C. 7cm D. 8cm
9.如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为 .
10.(2015 义乌市)如图,已知点A(0,1),B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于 度.
11.如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD= cm.
12、如图将半径为4米的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为 米.
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
(12题图) (14题图) (15题图)
13、CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.8 B.2 C.2或8 D.3或7
14、如图,在⊙O中,AB是直径,BC是弦,点P是上任意一点.若AB=5,BC=3,则AP的长不可能为( )
A.3 B. 4 C. D. 5
15、如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8cm B.cm C.6cm D.2cm
16、如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
17、如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
参考答案
1、C 2、D. 3、 0.8 4、B. 5、 B.6、D.7.B.8.B.9. .10. 60
11. 8 12、 4 13、C 14、A 15、A
16、解:过点O作OE⊥AB于点E,连接OB,
∵AB=8cm,∴AE=BE=AB=×8=4cm,
∵⊙O的直径为10cm,∴OB=×10=5cm,
∴OE===3cm,
∵垂线段最短,半径最长,
∴3cm≤OP≤5cm.
17、(1)证明:∵AD是直径,∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,,∴Rt△ABD≌Rt△ACD,∴∠BAD=∠CAD,
∵AB=AC,∴BE=CE;
(2)四边形BFCD是菱形.证明:∵AD是直径,AB=AC,∴AD⊥BC,BE=CE,
∵CF∥BD,∴∠FCE=∠DBE,
在△BED和△CEF中,∴△BED≌△CEF,∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,∴CE2=DE AE,设DE=x,
∵BC=8,AD=10,
∴42=x(10﹣x),
解得:x=2或x=8(舍去)
在Rt△CED中,
CD===2.
一、知识梳理
1、垂径定理: 。
2、垂径定理推论: 。
二、典例精析
1、如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.= B.= C.OF=CF D.AF=BF
(1题图) (3题图) (4题图) (5题图) (6题图)
2、下列下列说法中,正确的是( )
A.平分一条直径的弦必垂直于这条直径B.平分一条弧的直线垂直于这条弧所对的弦
C.弦的垂线必经过这条弦所在圆的圆心
D.在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心
3、如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为 m.
三、全面练习
4、如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
A.CE=DE B. AE=OE C. = D. △OCE≌△ODE
5、如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
A.3cm B. 4cm C. 5cm D. 6cm
6、一条排水管的截面如图所示,已知该排水管的半径OA=10,水面宽AB=16,则排水管内水的最大深度CD的长为( )
A.8 B. 6 C. 5 D. 4
7、如图,在等边△ABC中,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=1,那么△ABC的面积为( )
A.3 B. C. 4 D.
(7题图) (8题图) (9题图) (10题图) (11题图)
8、如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为( )
A.5cm B. 6cm C. 7cm D. 8cm
9.如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为 .
10.(2015 义乌市)如图,已知点A(0,1),B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于 度.
11.如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD= cm.
12、如图将半径为4米的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为 米.
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
(12题图) (14题图) (15题图)
13、CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.8 B.2 C.2或8 D.3或7
14、如图,在⊙O中,AB是直径,BC是弦,点P是上任意一点.若AB=5,BC=3,则AP的长不可能为( )
A.3 B. 4 C. D. 5
15、如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8cm B.cm C.6cm D.2cm
16、如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
17、如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
参考答案
1、C 2、D. 3、 0.8 4、B. 5、 B.6、D.7.B.8.B.9. .10. 60
11. 8 12、 4 13、C 14、A 15、A
16、解:过点O作OE⊥AB于点E,连接OB,
∵AB=8cm,∴AE=BE=AB=×8=4cm,
∵⊙O的直径为10cm,∴OB=×10=5cm,
∴OE===3cm,
∵垂线段最短,半径最长,
∴3cm≤OP≤5cm.
17、(1)证明:∵AD是直径,∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,,∴Rt△ABD≌Rt△ACD,∴∠BAD=∠CAD,
∵AB=AC,∴BE=CE;
(2)四边形BFCD是菱形.证明:∵AD是直径,AB=AC,∴AD⊥BC,BE=CE,
∵CF∥BD,∴∠FCE=∠DBE,
在△BED和△CEF中,∴△BED≌△CEF,∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,∴CE2=DE AE,设DE=x,
∵BC=8,AD=10,
∴42=x(10﹣x),
解得:x=2或x=8(舍去)
在Rt△CED中,
CD===2.
