5.5确定圆的条件同步辅导(含答案)
图片预览
文档简介
5.5确定圆的条件
一知识梳理
1、确定圆的条件:(1) (2) 。
2、直角三角形的外接圆的直径是 。
3、圆内接四边形的对角 ,外角等于它的 。
二、典例精析
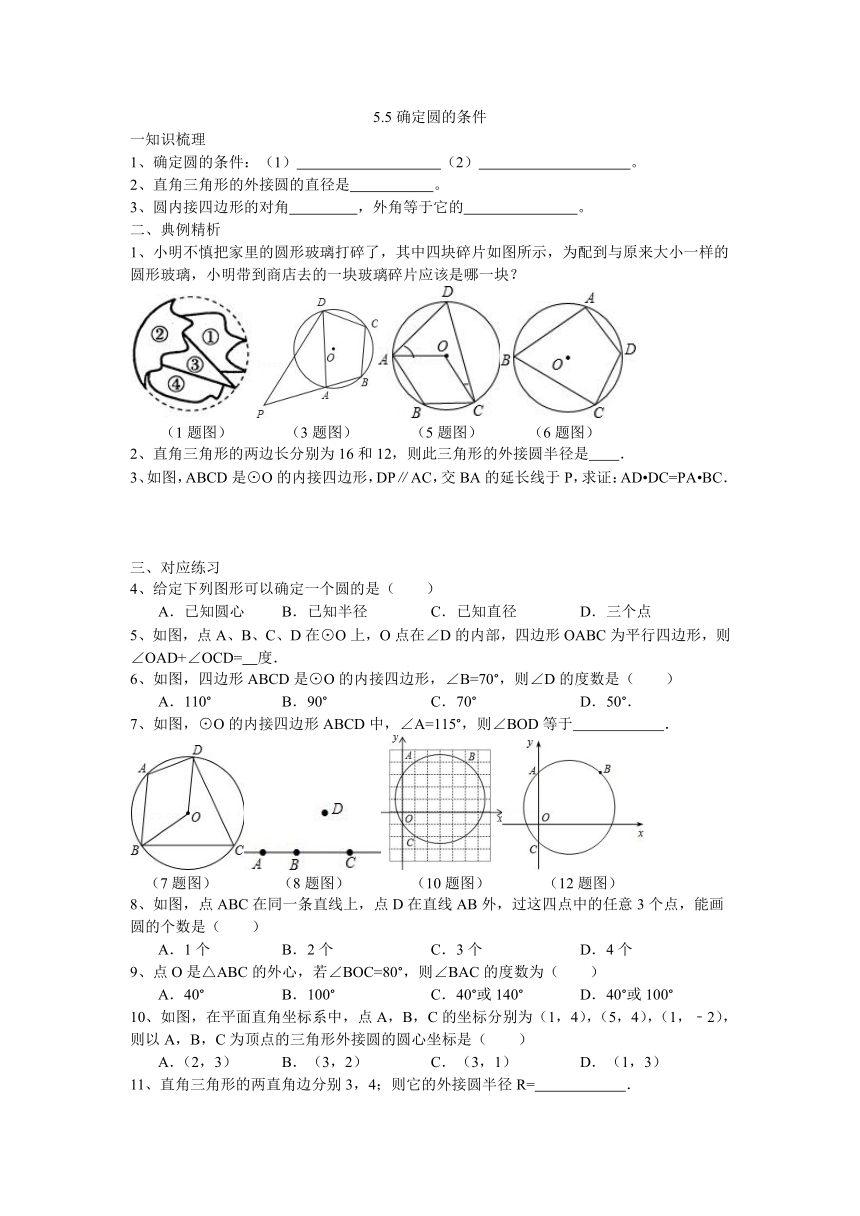
1、小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是哪一块?
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ) ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
(1题图) (3题图) (5题图) (6题图)
2、直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 .
3、如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD DC=PA BC.
三、对应练习
4、给定下列图形可以确定一个圆的是( )
A.已知圆心 B. 已知半径 C. 已知直径 D. 三个点
5、如图,点A、B、C ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= 度.
6、如图,四边形ABCD是⊙O的内接四边形,∠B=70°,则∠D的度数是( )
A.110° B. 90° C. 70° D. 50°.
7、如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于 .
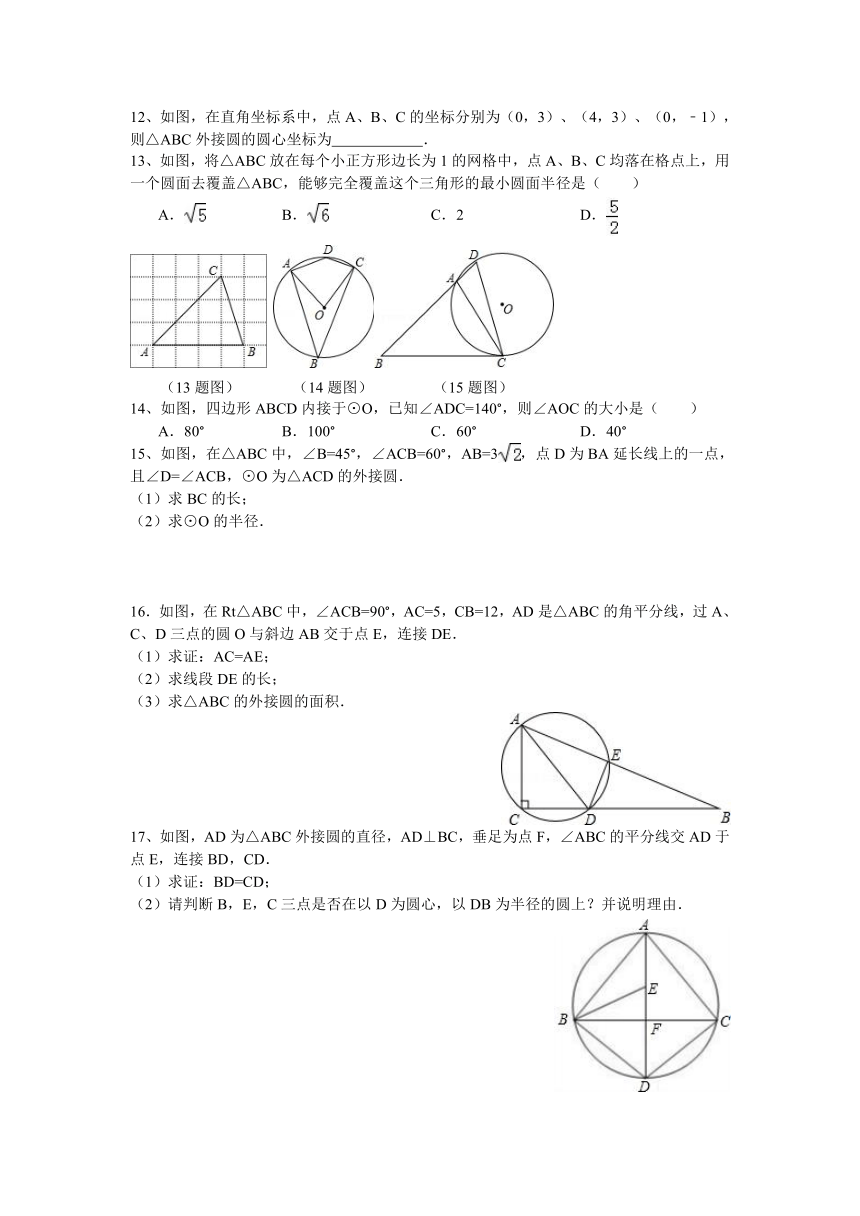
(7题图) (8题图) (10题图) (12题图)
8、如图,点ABC在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个 B. 2个 C. 3个 D. 4个
9、点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B. 100° C. 40°或140° D. 40°或100°
10、如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,﹣2),则以A,B,C为顶点的三角形外接圆的圆心坐标是( )
A.(2,3) B. (3,2) C. (3,1) D. (1,3)
11、直角三角形的两直角边分别3,4;则它的外接圆半径R= .
12、如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 .
13、如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A. B. C. 2 D.
(13题图) (14题图) (15题图)
14、如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
A.80° B. 100° C. 60° D. 40°
15、如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
16.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求线段DE的长;
(3)求△ABC的外接圆的面积.
17、如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
参考答案
1、② 2、8或10 3、证明:如图,连接AC,连接BD.∵DP∥AC,∴∠PDA=∠DAC.
∵∠DAC=∠DBC,∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,∴∠DAP=∠DCB.∴△PAD∽△DCB.
得PA:DC=AD:BC,即AD DC=PA BC.
4、C 5、 60 度6、A.7、 65 °.8、C. 9、C. 10、A
11、2或2.5 12、(2,1) 13、A.14、A
15、解:(1)过点A作AE⊥BC,垂足为E,∴∠AEB=∠AEC=90°,
在Rt△ABE中,∵sinB=,∴AE=ABsinB=3sin45°=3×=3,
∵∠B=45°,∴∠BAE=45°,∴BE=AE=3,
在Rt△ACE中,∵tan∠ACB=,
∴EC====,∴BC=BE+EC=3+;
(2)连接AO并延长到⊙O上一点M,连接CM,
由(1)得,在Rt△ACE中,∵∠EAC=30°,EC=,∴AC=2,
∵∠D=∠M=60°,∴sin60°===,解得:AM=4,∴⊙O的半径为2.
16、(1)证明:∵∠ACB=90°,且∠ACB为圆O的圆周角,
∴AD为圆O的直径,∴∠AED=90°,
又∵AD是△ABC的∠BAC的平分线,∴∠CAD=∠EAD,∴CD=DE
在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴AC=AE
(2)解:∵在Rt△ABC中,∠ACB=90°,AC=5,CB=12,∴AB===13,
设DE=x,则BD=12﹣x,BE=13﹣5=8,故x2+82=(12﹣x)2,解得:x=,
故DE的长为:;
(3)解:由(2)得:△ABC外接圆的半径=AB=×13=,面积为:π×()2=π.
17、(1)证明:∵AD为直径,AD⊥BC,∴∴BD=CD.
(2)B,E,C三点在以D为圆心,以DB为半径的圆上.理由:由(1)知:,
∴∠BAD=∠CBD,
又∵BE平分∠ABC,∴∠CBE=∠ABE,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,∠CBE=∠ABE,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD
∴DB=DE=DC.
∴B,E,C三点在以D为圆心,以DB为半径的圆上.
一知识梳理
1、确定圆的条件:(1) (2) 。
2、直角三角形的外接圆的直径是 。
3、圆内接四边形的对角 ,外角等于它的 。
二、典例精析
1、小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是哪一块?
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ) ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
(1题图) (3题图) (5题图) (6题图)
2、直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 .
3、如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD DC=PA BC.
三、对应练习
4、给定下列图形可以确定一个圆的是( )
A.已知圆心 B. 已知半径 C. 已知直径 D. 三个点
5、如图,点A、B、C ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= 度.
6、如图,四边形ABCD是⊙O的内接四边形,∠B=70°,则∠D的度数是( )
A.110° B. 90° C. 70° D. 50°.
7、如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于 .
(7题图) (8题图) (10题图) (12题图)
8、如图,点ABC在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画圆的个数是( )
A.1个 B. 2个 C. 3个 D. 4个
9、点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B. 100° C. 40°或140° D. 40°或100°
10、如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,﹣2),则以A,B,C为顶点的三角形外接圆的圆心坐标是( )
A.(2,3) B. (3,2) C. (3,1) D. (1,3)
11、直角三角形的两直角边分别3,4;则它的外接圆半径R= .
12、如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,﹣1),则△ABC外接圆的圆心坐标为 .
13、如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A. B. C. 2 D.
(13题图) (14题图) (15题图)
14、如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
A.80° B. 100° C. 60° D. 40°
15、如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
16.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求线段DE的长;
(3)求△ABC的外接圆的面积.
17、如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
参考答案
1、② 2、8或10 3、证明:如图,连接AC,连接BD.∵DP∥AC,∴∠PDA=∠DAC.
∵∠DAC=∠DBC,∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,∴∠DAP=∠DCB.∴△PAD∽△DCB.
得PA:DC=AD:BC,即AD DC=PA BC.
4、C 5、 60 度6、A.7、 65 °.8、C. 9、C. 10、A
11、2或2.5 12、(2,1) 13、A.14、A
15、解:(1)过点A作AE⊥BC,垂足为E,∴∠AEB=∠AEC=90°,
在Rt△ABE中,∵sinB=,∴AE=ABsinB=3sin45°=3×=3,
∵∠B=45°,∴∠BAE=45°,∴BE=AE=3,
在Rt△ACE中,∵tan∠ACB=,
∴EC====,∴BC=BE+EC=3+;
(2)连接AO并延长到⊙O上一点M,连接CM,
由(1)得,在Rt△ACE中,∵∠EAC=30°,EC=,∴AC=2,
∵∠D=∠M=60°,∴sin60°===,解得:AM=4,∴⊙O的半径为2.
16、(1)证明:∵∠ACB=90°,且∠ACB为圆O的圆周角,
∴AD为圆O的直径,∴∠AED=90°,
又∵AD是△ABC的∠BAC的平分线,∴∠CAD=∠EAD,∴CD=DE
在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴AC=AE
(2)解:∵在Rt△ABC中,∠ACB=90°,AC=5,CB=12,∴AB===13,
设DE=x,则BD=12﹣x,BE=13﹣5=8,故x2+82=(12﹣x)2,解得:x=,
故DE的长为:;
(3)解:由(2)得:△ABC外接圆的半径=AB=×13=,面积为:π×()2=π.
17、(1)证明:∵AD为直径,AD⊥BC,∴∴BD=CD.
(2)B,E,C三点在以D为圆心,以DB为半径的圆上.理由:由(1)知:,
∴∠BAD=∠CBD,
又∵BE平分∠ABC,∴∠CBE=∠ABE,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,∠CBE=∠ABE,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD
∴DB=DE=DC.
∴B,E,C三点在以D为圆心,以DB为半径的圆上.
