数学:16.5三角形的中位线定理教案3(北京课改版八年级下)
文档属性
| 名称 | 数学:16.5三角形的中位线定理教案3(北京课改版八年级下) |

|
|
| 格式 | rar | ||
| 文件大小 | 51.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-30 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
三角形的中位线
一、教学目标设计
本节课的认知目的是使学生了解三角形的中位线概念及其性质定理,重点是熟悉和掌握三角形中位线定理,并能正确地运用这个定理去解决一些简单的几何问题。
本节课利用几何画版平台,动态演示了例题几何图形的多种变化,使学生
初步认识事物的动与静、变与不变这一矛盾的对立与统一的辨证唯物主义思想。
二、教学内容及重点、难点分析
三角形中位线定理是三角形的一个重要性质,本节课的重点之一是掌握定理的实质:在同一个题设下有两个独立的结论,一个结论是表明位置关系,另一个结论是表明数量关系。一定要向学生说明,在应用这个定理时,可以同时用两个结论,也可以只选用平行关系,或只选用倍分关系,要根据具体情况按需选用。
本节课的另一重点是定理的应用,必要时须添加辅助线,将四边形分成两个
(或两个以上)含有中位线的三角形。
本节课的难点是定理的证明,课本用的是同一法思想,但又不是规范的同一
法证明,因此只要学生阅读了解即可,不作为重点讲解。
三、教学对象分析
初二的学生,已经掌握了几何最基本的分析和推理方法,大多数学生都能独
立完成例题的证明和课后的练习。但思维的灵活性和多样化还有限,在熟知课本
知识的基础上不失时机地灌输新的数学思想和思维方式很有必要,对他们今后的
学习将起到一个重大的转变。
四、教学策略及教法设计
本节课是一个探索性课型,改变以往只着重推理证明的教学模式,而是先探索再结论。教学设计的宗旨是:取材源于课本又高于课本;选题多于课本而决不超纲。教学策略是利用几何画板动态演示例题图形的多种变化,使学生意识到我们平常所看到的静态几何图形,只是动态图形在运动过程中的某一瞬间,在动态中探索图形变化的规律,在静态中寻求解决问题的方案,题变而理(推理的依据和方法)不变,思维导向从一般到特殊,再回到更一般,前后连贯,一气呵成,课堂容量大而教学效果好,充分显示了多媒体教学的优势。
五、教学媒体设计
本多媒体课件用 Authorware 制作,并引进几何画板,课件设计力求简洁、精细、美观、明了,交互方便。主页突出课题和主目录,主目录设置层次较高,始终显现于画面,可随时点击任何一个目录,打开你所需要的一页。若要程序
继续进行,只需按空格键或点击鼠标。可自由控制课堂节奏。
六、教学过程设计和分析
教 学 过 程 设计思路及应用分析
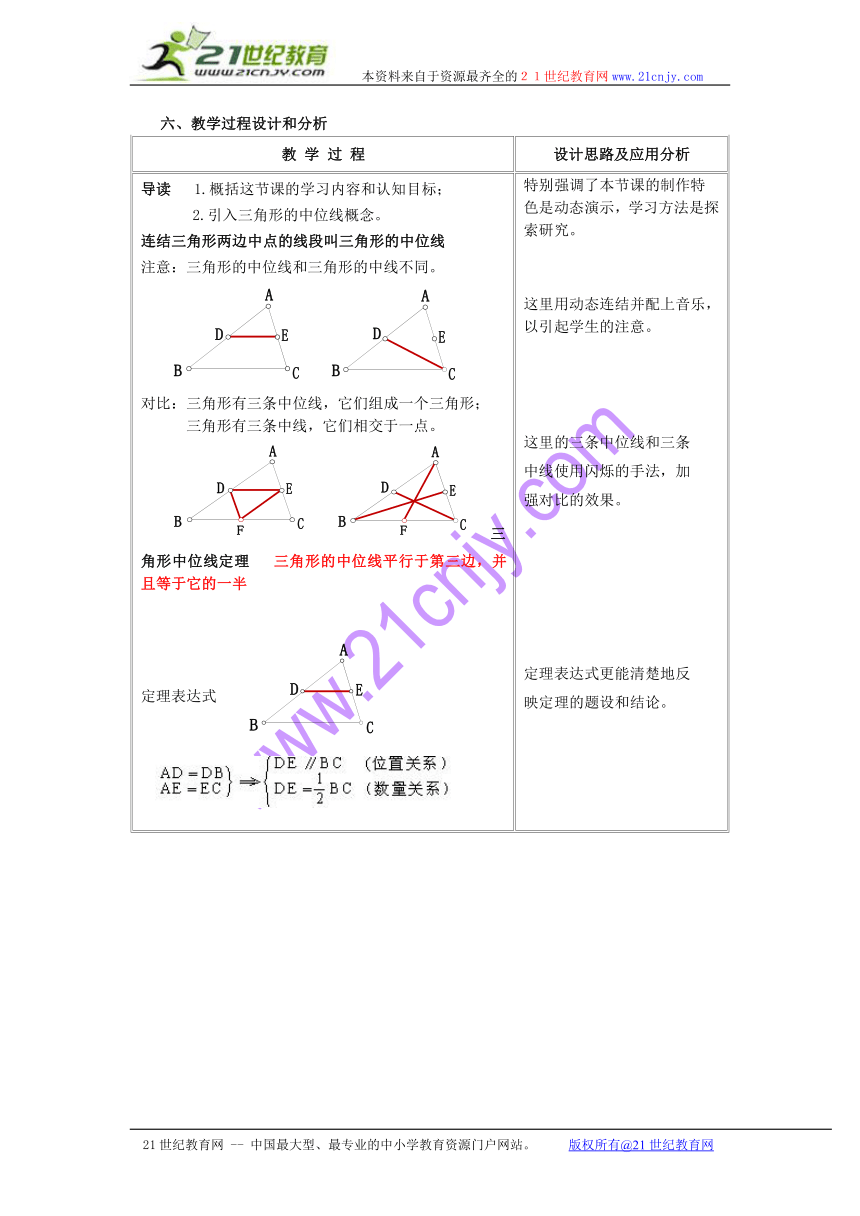
导读 1.概括这节课的学习内容和认知目标;2.引入三角形的中位线概念。连结三角形两边中点的线段叫三角形的中位线注意:三角形的中位线和三角形的中线不同。 对比:三角形有三条中位线,它们组成一个三角形;三角形有三条中线,它们相交于一点。 三角形中位线定理 三角形的中位线平行于第三边,并且等于它的一半定理表达式 特别强调了本节课的制作特色是动态演示,学习方法是探索研究。这里用动态连结并配上音乐,以引起学生的注意。这里的三条中位线和三条中线使用闪烁的手法,加强对比的效果。定理表达式更能清楚地反映定理的题设和结论。
证明:延长DE到F,使EF=DE,连结CF.演示:打开几何画板1.依次拖动三角形的三个顶点,注意DE 和 BC长度的变化,观察它们的数量关系。2.自点 D 作 BC 的平行线 FG,再拖动三个顶点,观察 DE 与 BC 的位置关系。例题 求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。 已知:如图,在四边形 ABCD 中,E、F、G、H 分别是 AB、BC、CD、DA 的中点。 求证:四边形 EFGH 是平行四边形。证法一:联结 AC.证法二:连结 AC、BD.继续运行程序可以看到,把等量关系改为平行关系,证明过程完全相同。探索:把例题中的四边形 ABCD 称为原四边形,顺次连结四边中点所得到的四边形叫做中点四边形,可知,如果原四边形是凸四边形,其中点四边形是平行四边形。探索一:若原四边形是矩形、菱形、等腰梯形,那么中点四边形是什么图形?探索二:若原四边形的对角线垂直、或相等、或垂直且相等,那么中点四边形是什么图形?探索三:若原四边形改变形状,中点四边形有什么变化?打开几何画板探索一 观察1ABCD是矩形,EFGH是什么四边形。观察2ABCD是菱形,EFGH是什么四边形。观察3ABCD是等腰梯形,EFGH是什么四边形。打开几何画板探索二观察1.ABCD对角线互相垂直,EFGH是什么四边形。观察2.ABCD对角线相等,EFGH是什么四边形。观察3.ABCD对角线垂直且相等,EFGH是什么四边形。打开几何画板探索三变化1.ABCD变为凹四边形。变化2.ABCD变为扭曲四边形。变化3.AB与BC重合。动画:设置A、B、C、D四点在某一轨道上不停地运动,四边形ABCD的形状也不停地变化,可以发现,只要四条线段AB、BC、CD、DA首尾相连,四边形EFGH始终是平行四边形。只要在画面任何一处点击鼠标,图形即停止在一种静止状态。上面的三种图形都是运动过程中的某一瞬间。 可以让学生自己操作,图形静止后,根据当前的图形自编一道题。练习 1.如左下图,△ABC中,D、E、F 分别为AB、BC、CA的中点,∠DEF = ∠BAC 吗? 2.如右下图,△ABC中,AG 是 BC边的高,D、F是AB、AC的中点,∠DGF = BAC 吗?3.把上面两个图形合并在一起,如下图,根据合并后的图形编一道题,并证明你的结论。作业 1.求证:顺次连结矩形四边中点所得的四边形是菱形。2.求证:顺次连结菱形四边中点所得的四边形是矩形。课堂小结1.中位线定理在同一条件下有两个结论,一是表明位置关系,一是表明数量关系,应用时要根据需要而选择。2.在应用中位线解四边形问题时,关键是作辅助线,构造含有中位线的三角形。 3.我们平常见到的几何图形都是静态的,本节课利用几何画板演示了动态图形的变化,可以清楚地看到几何图形的位置关系处在相互依存的状态之中,静态图形只是动态图形在变化过程中的某一瞬间。动是绝对的,静是相对的,在动态中探索图形变化的规律,在静态中寻求解决问题的方案,这正是数学这门学科的创新和发展。 中位线定理的证明方法较多,因为不作为本节课的重点,所以这里只选用了一种学生比较熟悉的直接证法。也可以先演示再证明,通过演示,使学生更直观地了解三角形的中位线和第三边的数量关系以及位置关系。说明:关闭几何画板时,选择“不保存”。本例题选自课本,证法一与课本相同。引导学生分析为什么要连辅助线。这里增加的证法二,是让学生知道单独使用定理的两个结论同样可以达到目的。这里运用了Authorware的擦除和显现效果,把“=”号渐变为“∥”号,节省从新书写的时间,且又起到对比的效果。这里的探索是本节课的重点,也是最能吸引学生注意力的一种教学手段。利用几何画板制作动态演示,可以清楚地看到每个不同的图形都处在变化的过程当中。每幅画面都安置了四个按钮,每双击一个按钮,原四边形即可缓慢演变为矩形、菱形、等腰梯形等,(顺序可以随意)。学生可以根据显示的线段长度及有关角度来判断原四边形和中点四边形的形状。再双击“变化”,即可看到变化的全过程。使学生感受到不同的静态图形只是动态图形在运动过程中的某一瞬间。在探索二之前,可以设疑提问:当中点四边形是矩形或菱形时,原四边形是什么图形?探索三中的动画设计与前面的动态设计不同,前面用的是几何画板中的移动效果,把四个顶点A、B、C、D动态移动到某一固定位置,得到一种特殊的静止图形,以便对这种图形分析研究。而动画则是不停地运动,观察到的图形更加多样化和一般化。这就是从一般到特殊,再回到更一般的思维方式。本课件可以让学生动手动脑,完成观察、分析、探索、结论这一学习过程。这道练习分三步完成,第2小题是把三角形的中位线和直角三角形斜边的中线加以对比,区分使用,第3小题则是两个知识概念的综合应用。这里运用Authorware的移动效果将两个图形合并。课堂着重探索,结论的证明让学生课后完成。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
三角形的中位线
一、教学目标设计
本节课的认知目的是使学生了解三角形的中位线概念及其性质定理,重点是熟悉和掌握三角形中位线定理,并能正确地运用这个定理去解决一些简单的几何问题。
本节课利用几何画版平台,动态演示了例题几何图形的多种变化,使学生
初步认识事物的动与静、变与不变这一矛盾的对立与统一的辨证唯物主义思想。
二、教学内容及重点、难点分析
三角形中位线定理是三角形的一个重要性质,本节课的重点之一是掌握定理的实质:在同一个题设下有两个独立的结论,一个结论是表明位置关系,另一个结论是表明数量关系。一定要向学生说明,在应用这个定理时,可以同时用两个结论,也可以只选用平行关系,或只选用倍分关系,要根据具体情况按需选用。
本节课的另一重点是定理的应用,必要时须添加辅助线,将四边形分成两个
(或两个以上)含有中位线的三角形。
本节课的难点是定理的证明,课本用的是同一法思想,但又不是规范的同一
法证明,因此只要学生阅读了解即可,不作为重点讲解。
三、教学对象分析
初二的学生,已经掌握了几何最基本的分析和推理方法,大多数学生都能独
立完成例题的证明和课后的练习。但思维的灵活性和多样化还有限,在熟知课本
知识的基础上不失时机地灌输新的数学思想和思维方式很有必要,对他们今后的
学习将起到一个重大的转变。
四、教学策略及教法设计
本节课是一个探索性课型,改变以往只着重推理证明的教学模式,而是先探索再结论。教学设计的宗旨是:取材源于课本又高于课本;选题多于课本而决不超纲。教学策略是利用几何画板动态演示例题图形的多种变化,使学生意识到我们平常所看到的静态几何图形,只是动态图形在运动过程中的某一瞬间,在动态中探索图形变化的规律,在静态中寻求解决问题的方案,题变而理(推理的依据和方法)不变,思维导向从一般到特殊,再回到更一般,前后连贯,一气呵成,课堂容量大而教学效果好,充分显示了多媒体教学的优势。
五、教学媒体设计
本多媒体课件用 Authorware 制作,并引进几何画板,课件设计力求简洁、精细、美观、明了,交互方便。主页突出课题和主目录,主目录设置层次较高,始终显现于画面,可随时点击任何一个目录,打开你所需要的一页。若要程序
继续进行,只需按空格键或点击鼠标。可自由控制课堂节奏。
六、教学过程设计和分析
教 学 过 程 设计思路及应用分析
导读 1.概括这节课的学习内容和认知目标;2.引入三角形的中位线概念。连结三角形两边中点的线段叫三角形的中位线注意:三角形的中位线和三角形的中线不同。 对比:三角形有三条中位线,它们组成一个三角形;三角形有三条中线,它们相交于一点。 三角形中位线定理 三角形的中位线平行于第三边,并且等于它的一半定理表达式 特别强调了本节课的制作特色是动态演示,学习方法是探索研究。这里用动态连结并配上音乐,以引起学生的注意。这里的三条中位线和三条中线使用闪烁的手法,加强对比的效果。定理表达式更能清楚地反映定理的题设和结论。
证明:延长DE到F,使EF=DE,连结CF.演示:打开几何画板1.依次拖动三角形的三个顶点,注意DE 和 BC长度的变化,观察它们的数量关系。2.自点 D 作 BC 的平行线 FG,再拖动三个顶点,观察 DE 与 BC 的位置关系。例题 求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。 已知:如图,在四边形 ABCD 中,E、F、G、H 分别是 AB、BC、CD、DA 的中点。 求证:四边形 EFGH 是平行四边形。证法一:联结 AC.证法二:连结 AC、BD.继续运行程序可以看到,把等量关系改为平行关系,证明过程完全相同。探索:把例题中的四边形 ABCD 称为原四边形,顺次连结四边中点所得到的四边形叫做中点四边形,可知,如果原四边形是凸四边形,其中点四边形是平行四边形。探索一:若原四边形是矩形、菱形、等腰梯形,那么中点四边形是什么图形?探索二:若原四边形的对角线垂直、或相等、或垂直且相等,那么中点四边形是什么图形?探索三:若原四边形改变形状,中点四边形有什么变化?打开几何画板探索一 观察1ABCD是矩形,EFGH是什么四边形。观察2ABCD是菱形,EFGH是什么四边形。观察3ABCD是等腰梯形,EFGH是什么四边形。打开几何画板探索二观察1.ABCD对角线互相垂直,EFGH是什么四边形。观察2.ABCD对角线相等,EFGH是什么四边形。观察3.ABCD对角线垂直且相等,EFGH是什么四边形。打开几何画板探索三变化1.ABCD变为凹四边形。变化2.ABCD变为扭曲四边形。变化3.AB与BC重合。动画:设置A、B、C、D四点在某一轨道上不停地运动,四边形ABCD的形状也不停地变化,可以发现,只要四条线段AB、BC、CD、DA首尾相连,四边形EFGH始终是平行四边形。只要在画面任何一处点击鼠标,图形即停止在一种静止状态。上面的三种图形都是运动过程中的某一瞬间。 可以让学生自己操作,图形静止后,根据当前的图形自编一道题。练习 1.如左下图,△ABC中,D、E、F 分别为AB、BC、CA的中点,∠DEF = ∠BAC 吗? 2.如右下图,△ABC中,AG 是 BC边的高,D、F是AB、AC的中点,∠DGF = BAC 吗?3.把上面两个图形合并在一起,如下图,根据合并后的图形编一道题,并证明你的结论。作业 1.求证:顺次连结矩形四边中点所得的四边形是菱形。2.求证:顺次连结菱形四边中点所得的四边形是矩形。课堂小结1.中位线定理在同一条件下有两个结论,一是表明位置关系,一是表明数量关系,应用时要根据需要而选择。2.在应用中位线解四边形问题时,关键是作辅助线,构造含有中位线的三角形。 3.我们平常见到的几何图形都是静态的,本节课利用几何画板演示了动态图形的变化,可以清楚地看到几何图形的位置关系处在相互依存的状态之中,静态图形只是动态图形在变化过程中的某一瞬间。动是绝对的,静是相对的,在动态中探索图形变化的规律,在静态中寻求解决问题的方案,这正是数学这门学科的创新和发展。 中位线定理的证明方法较多,因为不作为本节课的重点,所以这里只选用了一种学生比较熟悉的直接证法。也可以先演示再证明,通过演示,使学生更直观地了解三角形的中位线和第三边的数量关系以及位置关系。说明:关闭几何画板时,选择“不保存”。本例题选自课本,证法一与课本相同。引导学生分析为什么要连辅助线。这里增加的证法二,是让学生知道单独使用定理的两个结论同样可以达到目的。这里运用了Authorware的擦除和显现效果,把“=”号渐变为“∥”号,节省从新书写的时间,且又起到对比的效果。这里的探索是本节课的重点,也是最能吸引学生注意力的一种教学手段。利用几何画板制作动态演示,可以清楚地看到每个不同的图形都处在变化的过程当中。每幅画面都安置了四个按钮,每双击一个按钮,原四边形即可缓慢演变为矩形、菱形、等腰梯形等,(顺序可以随意)。学生可以根据显示的线段长度及有关角度来判断原四边形和中点四边形的形状。再双击“变化”,即可看到变化的全过程。使学生感受到不同的静态图形只是动态图形在运动过程中的某一瞬间。在探索二之前,可以设疑提问:当中点四边形是矩形或菱形时,原四边形是什么图形?探索三中的动画设计与前面的动态设计不同,前面用的是几何画板中的移动效果,把四个顶点A、B、C、D动态移动到某一固定位置,得到一种特殊的静止图形,以便对这种图形分析研究。而动画则是不停地运动,观察到的图形更加多样化和一般化。这就是从一般到特殊,再回到更一般的思维方式。本课件可以让学生动手动脑,完成观察、分析、探索、结论这一学习过程。这道练习分三步完成,第2小题是把三角形的中位线和直角三角形斜边的中线加以对比,区分使用,第3小题则是两个知识概念的综合应用。这里运用Authorware的移动效果将两个图形合并。课堂着重探索,结论的证明让学生课后完成。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
