2023-2024学年 苏科版数学八年级下册9.5 三角形的中位线 同步练习(无答案)
文档属性
| 名称 | 2023-2024学年 苏科版数学八年级下册9.5 三角形的中位线 同步练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 272.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 16:19:41 | ||
图片预览

文档简介
9.5 三角形的中位线
一.选择题
1.一个三角形的三条中位线的长为6、7、8,则此三角形的周长为( )
A.40 B.41 C.42 D.43
2.如图,D是内一点,,,,,E、F、G、H分别是、、、的中点,则四边形的周长是( )
A.7 B.9 C.11 D.13
3.如图,在中,,点D,E分别是,的中点,若点F在线段上,且,则的度数为( )
A. B. C. D.
4.如图, 的对角线,交于点,平分交于点,且,,连接.下列结论:①;②;③;④,成立的个数有( )
A.1个 B.2个 C.3个 D.4个
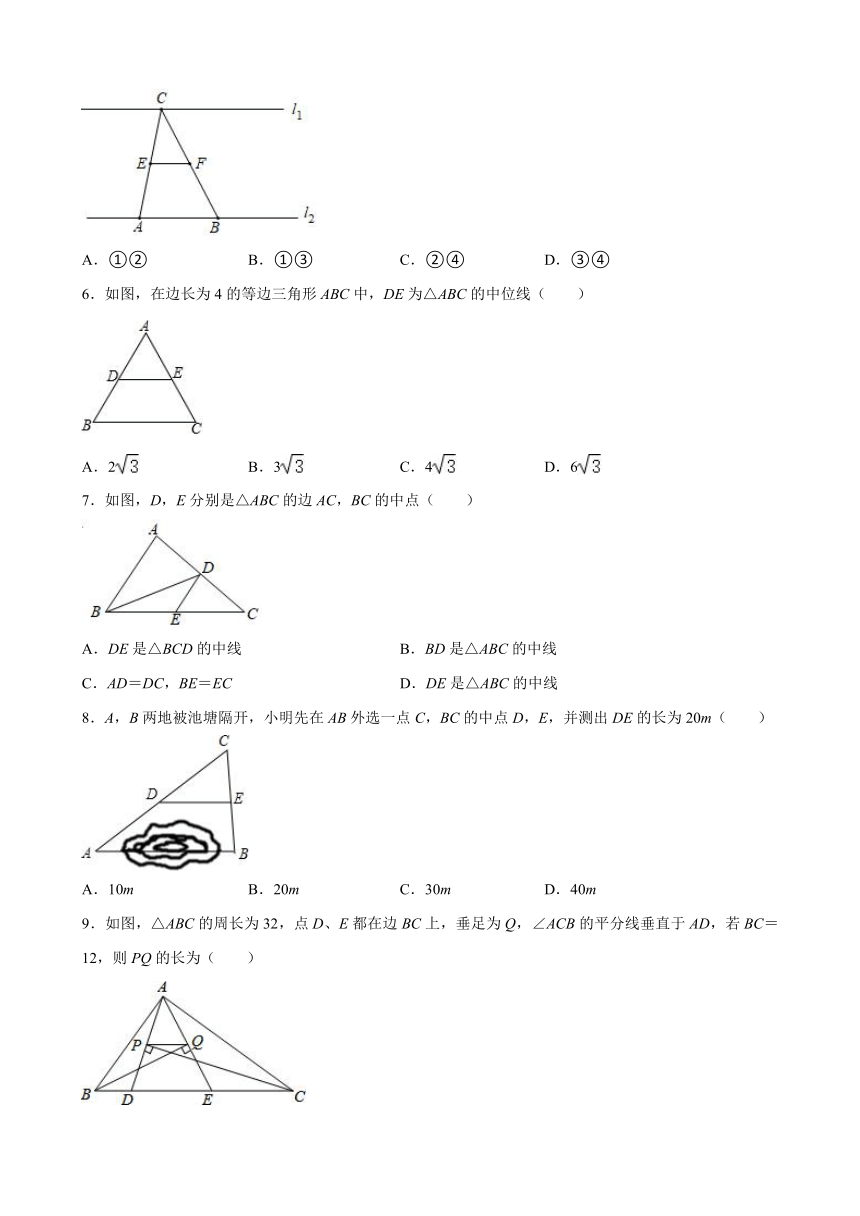
5.如图,直线l1∥l2,点A、B固定在直线l2上,点C是直线l1上一动点,若点E、F分别为CA、CB中点,对于下列各值:①线段EF的长;③△CEF的面积;④∠ECF的度数( )
A.①② B.①③ C.②④ D.③④
6.如图,在边长为4的等边三角形ABC中,DE为△ABC的中位线( )
A.2 B.3 C.4 D.6
7.如图,D,E分别是△ABC的边AC,BC的中点( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.DE是△ABC的中线
8.A,B两地被池塘隔开,小明先在AB外选一点C,BC的中点D,E,并测出DE的长为20m( )
A.10m B.20m C.30m D.40m
9.如图,△ABC的周长为32,点D、E都在边BC上,垂足为Q,∠ACB的平分线垂直于AD,若BC=12,则PQ的长为( )
A.3 B.4 C.5 D.6
10.如图,顺次连接△ABC三边的中点D,E,F得到的三角形面积为S1,顺次连接△CEF三边的中点M,G,H得到的三角形面积为S2,顺次连接△CGH三边的中点得到的三角形面积为S3,设△ABC的面积为64,则S1+S2+S3=( )
A.21 B.24 C.27 D.32
二.填空题
1.如图,在△ABC中,已知AB=8,点D,E分别为BC,BF平分∠ABC交DE于点F,则EF的长为 .
2.如图,在Rt△ABC中,∠C=90°,D,E分别是AC,AB的中点.将线段DE绕着点E逆时针能转角α(0°<α≤180°),连接BD′,若△D'BE是直角三角形 °.
3.如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,若DE=1,则FG= .
4.如图,四边形ABCD中,AB=CD=6,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S .
5.如图,AC,BD是四边形ABCD的对角线,F分别是AD,BC的中点,N分别是AC,BD的中点,MF,FN,若AB=CD=2,则四边形ENFM的周长是 .
三.解答题
1.如图,△ABC中,过点A分别作∠ABC,AE.D,E为垂足
(1)ED∥BC;
(2)ED=(AB+AC+BC).
2.如图,在平面直角坐标系中,点B在x轴正半轴上,点A的坐标为(0,6),点P在线段AB上,∠OAB=∠AOP=30°.
(1)求点P的坐标;
(2)将△AOP绕点O顺时针方向旋转,旋转角度为α(0°<α<180°),旋转中的三角形记为△A1OP1(点A、P的对应点分别A1、P1),在旋转过程中,直线OA1交直线AB于点M,直线OP1交直线AB于点N,当△OMN为等腰三角形时,请直接写出α的值.
3.我们已经学行四边形的知识,借助平行四边形的相关性质、判定定理,我们研究学习了三角形的中位线的定义和性质.根据研究图形的规律,请回答以下问题:
(1)三角形中位线定理是:__________________________________________
(2)梯形也是一种常见的四边形,它是有一组对边平行,另一组对边不平行的四边形,连接梯形两腰的中点,得到的线段叫做梯形的中位线.
①请在图中画出梯形的中位线;(请在答题卡上画出此梯形后,画出梯形中位线)
②通过观察、度量、猜想梯形中位线具有的性质并证明.
猜想:梯形的中位线________________.(请在答题卡上把这句话写全)
已知:
求证:
证明:
4.如图,在四边形ABCD中,AB=CD,连接EF并延长,分别与BA,N,则∠BME=∠CNE(不必证明)
(温馨提示:在图(1)中,连接BD,取BD的中点H,根据三角形中位线定理,证明HE=HF,再利用平行线的性质,可证明∠BME=∠CNE)
(1)如图(2),在四边形ADBC中,AB与CD相交于点O,E.F分别是BC.AD的中点,连接EF,判断△OMN的形状,请直接写出结论.
(2)如图(3)中,在△ABC中,AC>AB,AB=CD,E.F分别是BC.AD的中点,与BA的延长线交于点G,若∠EFC=60°,判断△AGD形状并证明.
一.选择题
1.一个三角形的三条中位线的长为6、7、8,则此三角形的周长为( )
A.40 B.41 C.42 D.43
2.如图,D是内一点,,,,,E、F、G、H分别是、、、的中点,则四边形的周长是( )
A.7 B.9 C.11 D.13
3.如图,在中,,点D,E分别是,的中点,若点F在线段上,且,则的度数为( )
A. B. C. D.
4.如图, 的对角线,交于点,平分交于点,且,,连接.下列结论:①;②;③;④,成立的个数有( )
A.1个 B.2个 C.3个 D.4个
5.如图,直线l1∥l2,点A、B固定在直线l2上,点C是直线l1上一动点,若点E、F分别为CA、CB中点,对于下列各值:①线段EF的长;③△CEF的面积;④∠ECF的度数( )
A.①② B.①③ C.②④ D.③④
6.如图,在边长为4的等边三角形ABC中,DE为△ABC的中位线( )
A.2 B.3 C.4 D.6
7.如图,D,E分别是△ABC的边AC,BC的中点( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.DE是△ABC的中线
8.A,B两地被池塘隔开,小明先在AB外选一点C,BC的中点D,E,并测出DE的长为20m( )
A.10m B.20m C.30m D.40m
9.如图,△ABC的周长为32,点D、E都在边BC上,垂足为Q,∠ACB的平分线垂直于AD,若BC=12,则PQ的长为( )
A.3 B.4 C.5 D.6
10.如图,顺次连接△ABC三边的中点D,E,F得到的三角形面积为S1,顺次连接△CEF三边的中点M,G,H得到的三角形面积为S2,顺次连接△CGH三边的中点得到的三角形面积为S3,设△ABC的面积为64,则S1+S2+S3=( )
A.21 B.24 C.27 D.32
二.填空题
1.如图,在△ABC中,已知AB=8,点D,E分别为BC,BF平分∠ABC交DE于点F,则EF的长为 .
2.如图,在Rt△ABC中,∠C=90°,D,E分别是AC,AB的中点.将线段DE绕着点E逆时针能转角α(0°<α≤180°),连接BD′,若△D'BE是直角三角形 °.
3.如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,若DE=1,则FG= .
4.如图,四边形ABCD中,AB=CD=6,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S .
5.如图,AC,BD是四边形ABCD的对角线,F分别是AD,BC的中点,N分别是AC,BD的中点,MF,FN,若AB=CD=2,则四边形ENFM的周长是 .
三.解答题
1.如图,△ABC中,过点A分别作∠ABC,AE.D,E为垂足
(1)ED∥BC;
(2)ED=(AB+AC+BC).
2.如图,在平面直角坐标系中,点B在x轴正半轴上,点A的坐标为(0,6),点P在线段AB上,∠OAB=∠AOP=30°.
(1)求点P的坐标;
(2)将△AOP绕点O顺时针方向旋转,旋转角度为α(0°<α<180°),旋转中的三角形记为△A1OP1(点A、P的对应点分别A1、P1),在旋转过程中,直线OA1交直线AB于点M,直线OP1交直线AB于点N,当△OMN为等腰三角形时,请直接写出α的值.
3.我们已经学行四边形的知识,借助平行四边形的相关性质、判定定理,我们研究学习了三角形的中位线的定义和性质.根据研究图形的规律,请回答以下问题:
(1)三角形中位线定理是:__________________________________________
(2)梯形也是一种常见的四边形,它是有一组对边平行,另一组对边不平行的四边形,连接梯形两腰的中点,得到的线段叫做梯形的中位线.
①请在图中画出梯形的中位线;(请在答题卡上画出此梯形后,画出梯形中位线)
②通过观察、度量、猜想梯形中位线具有的性质并证明.
猜想:梯形的中位线________________.(请在答题卡上把这句话写全)
已知:
求证:
证明:
4.如图,在四边形ABCD中,AB=CD,连接EF并延长,分别与BA,N,则∠BME=∠CNE(不必证明)
(温馨提示:在图(1)中,连接BD,取BD的中点H,根据三角形中位线定理,证明HE=HF,再利用平行线的性质,可证明∠BME=∠CNE)
(1)如图(2),在四边形ADBC中,AB与CD相交于点O,E.F分别是BC.AD的中点,连接EF,判断△OMN的形状,请直接写出结论.
(2)如图(3)中,在△ABC中,AC>AB,AB=CD,E.F分别是BC.AD的中点,与BA的延长线交于点G,若∠EFC=60°,判断△AGD形状并证明.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
