第19章《 一次函数 》单元同步检测试题(含答案)
文档属性
| 名称 | 第19章《 一次函数 》单元同步检测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 16:41:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.已知函数y=,则自变量x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠1 C.﹣1<x<1 D.x≠1
2.一次函数y=﹣2x+b上有两点A(2,m),B(3,n),则下列结论成立的是( )
A.m>n B.m<n C.m=n D.不能确定
6.将直线y=3x向下平移5个单位,再向左平移4个单位,得到直线( )
A.y=3x﹣1 B.y=3x﹣11 C.y=3x+7 D.y=3x+9
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.两条直线y1=kx﹣k与y2=﹣x在同一平面坐标系中的图象可能是( )
A.B. C.D.
6.如图,将点P(﹣1,3)向右平移n个单位后落在直线y=2x﹣1上的点P′处,则n等于( )
A.2 B.2.5 C.3 D.4
7.已知点A(﹣1,y1),点B(2,y2)在函数y=﹣3x+2的图象上,那么y1与y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
8.在平面直角坐标系中,已知点和点,当直线为常数与线段AB有交点时,k的取值范围为
A. 或 B.
C. 或 D. 或
9.如图,直线经过点,当时,则x的取值范围为
A. B. C. D.
10.如图1,在平面直角坐标系中, ABCD在第一象限,且轴.直线从原点O出发沿x轴正方向平移,在平移过程中,直线被 ABCD截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 ABCD的面积为
A. 3 B. C. 6 D.
二、填空题(每题3分,共30分)
11.函数y=中,自变量x的取值范围是 .
12.若y=(k+1)x|k|+m+4是一次函数,则k= .
13.写出一个过点(0,0)且函数值y随自变量x的增大而减小的一次函数关系式 .
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.汽车的剩余油量y(L)随着行驶的距离x(km)的变化而变化,若一辆车y与x之间的关系式为y=-0.08x,则y随x的增大而____________.
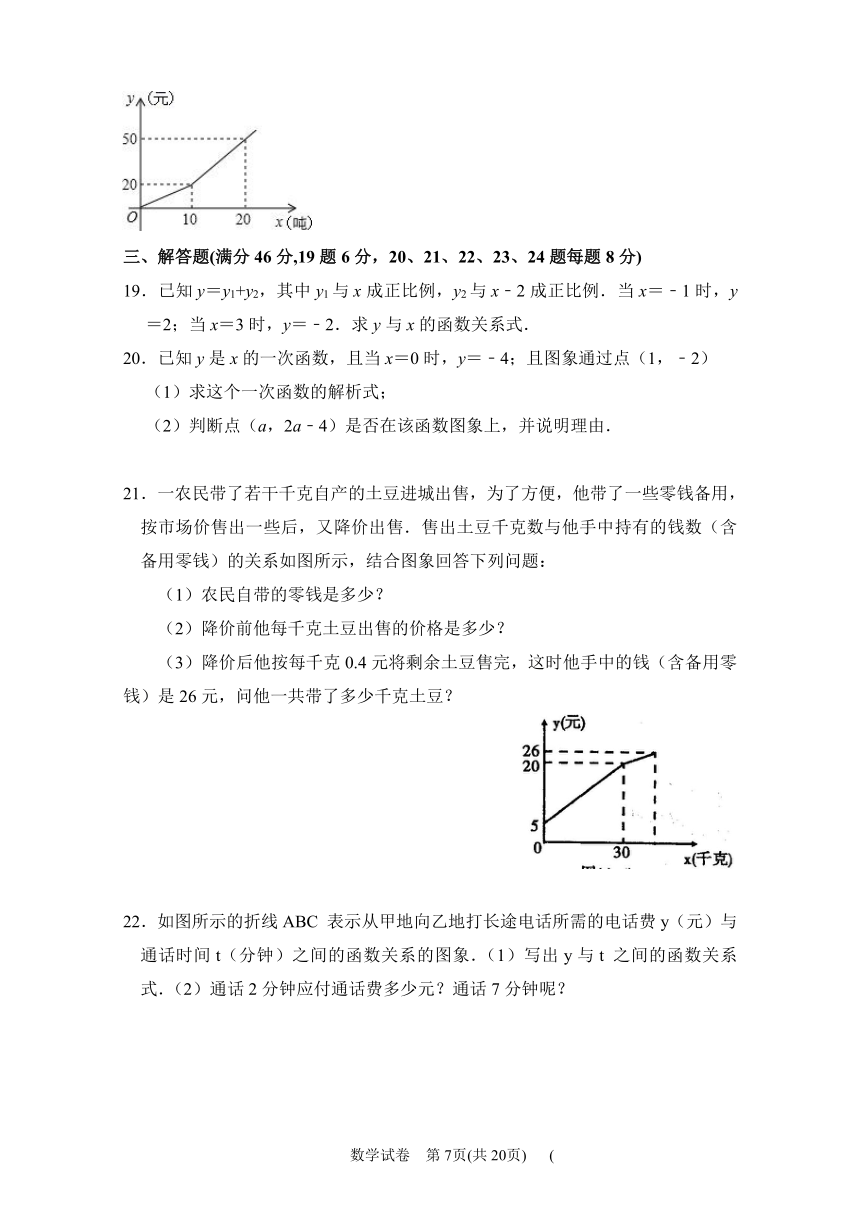
18.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费(元与用水量(吨之间的函数关系如图所示.按上述分段收费标准,小明家三、四月份分别交水费29元和18元,则四月份比三月份节约用水__吨.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知y=y1+y2,其中y1与x成正比例,y2与x﹣2成正比例.当x=﹣1时,y=2;当x=3时,y=﹣2.求y与x的函数关系式.
20.已知y是x的一次函数,且当x=0时,y=﹣4;且图象通过点(1,﹣2)
(1)求这个一次函数的解析式;
(2)判断点(a,2a﹣4)是否在该函数图象上,并说明理由.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.如图,已知长方形ABCD中,AB=CD=16,BC=DA=24,E为CD边的中点,P为长方形ABCD边上的动点,动点P以4个单位/秒的速度从A出发,沿着A→B→C→E运动到E点停止,设点P运动的时间为t秒,△APE的面积为y.
(1)求当t=2时,y的值是 ;当t=6时,y的值是 .
(2)点P运动过程中,求出y与t之间的关系式;
24.商丘市梁园区紧紧围绕十九大报告提出的阶段性目标任务,深化农业供给侧结构性改革,调整种植结构,深入进行了四大结构调整,分别是:水池铺乡的辣椒产业、刘口乡的杂果基地,孙福集乡的山药、莲藕产业,双八镇的草莓产业.目前,这四种产业享誉省内外.
某外地客商慕名来商丘考查,他准备购入山药和草莓进行试销,经市场调查,若购进山药和草莓各2箱共花费170元,购进山药3箱和草莓4箱共花费300元.
(1)求购进山药和草莓的单价;
(2)若该客商购进了山药和草莓共1000箱,其中山药销售单价为60元,草莓的销售单价为70元.设购进山药x箱,获得总利润为y元.
①求y关于x的函数关系式;
②由于草莓的保鲜期较短,该客商购进草莓箱数不超过山药箱数的,要使销售这批山药和草莓的利润最大,请你帮该客商设计一个进货方案,并求出其所获利润的最大值.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A A C D D A C B C A
二、填空题(每题3分,共24分)
11.
12.平行
13. y=3x
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:根据题意设y1=k1x,y2=k2(x﹣2),即y=y1+y2=k1x+k2(x﹣2),
将x=﹣1时,y=2;x=3时,y=﹣2分别代入得:,
解得:k1=﹣,k2=﹣,
则y=﹣x﹣(x﹣2)=﹣x+1.
即y与x的函数关系式为y=﹣x+1.
20.解:(1)设这个一次函数的解析式为y=kx+b(k≠0),
将(0,﹣4),(1,﹣2)代入y=kx+b,得:,
解得:.
∴这个一次函数的解析式为y=2x﹣4.
(2)点(a,2a﹣4)在该函数图象上,理由如下:
∵当x=a时,y=2a﹣4,
∴点(a,2a﹣4)在函数图象上.
21.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23.解:(1)长方形ABCD中,AB=CD=16,BC=DA=24,AD∥BC,∠BAD=∠B=∠C=∠D=90°,
∵P以4个单位/秒的速度从A出发,沿着A→B→C→E运动到E点停止,
∴当t=2时,则AP=4×2=8=AB,
即P为AB的中点,
∵E为CD边的中点,
∴四边形APED是矩形(如图1所示)
∴CE=DE=8,∠APE=∠B=90°,PE⊥AB,PE=BC=24
∴△APE的面积为;
当t=6时(如图2所示),
BP=6×4﹣AB=24﹣16=8,
∴PC=BC﹣BP﹣16
∴△APE的面积为;
故答案为:96;160;
(2)①当P在AB上时(如图1),
即0≤t≤4时,
此时,AP=4t,
∴△APE的面积为y=4t×24=48t,
②当点P在BC上时(如图2)
即4<t≤10,
此时BP=4t﹣16,
则PC=24﹣(4t﹣16)=40﹣4t
.
所以y与之间的关系式为y=﹣16t+256
③当P在CD上时(如图3)
即10<t≤12,
PE=48﹣4t,
∴△APE的面积为y=48﹣4t)×24=﹣48t+576.
24.解:(1)设购进每箱山药的单价为x元,购进每箱草莓的单价为y元,
根据题意得,
解得,
答:每箱山药的单价为40元,每箱草莓的单价为45元;
(2)①由题意可得,
y=(60﹣40)x+(70﹣45)(1000﹣x)=﹣5x+25000;
②由题意可得,
,
解得:x≥750,
又y=﹣5x+25000,k=﹣5<0,
∴y随x的增大而减小,
∴当x=750时,y达到最大值,即最大利润y=﹣5×750+25000=21250(元),
此时1000﹣x=1000﹣750=250(箱),
答:购进山药750箱,草莓250箱时所获利润最大,利润最大为21250元.
数学试卷 第19页(共22页) ( 数学试卷 第20页(共22页)
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.已知函数y=,则自变量x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠1 C.﹣1<x<1 D.x≠1
2.一次函数y=﹣2x+b上有两点A(2,m),B(3,n),则下列结论成立的是( )
A.m>n B.m<n C.m=n D.不能确定
6.将直线y=3x向下平移5个单位,再向左平移4个单位,得到直线( )
A.y=3x﹣1 B.y=3x﹣11 C.y=3x+7 D.y=3x+9
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.两条直线y1=kx﹣k与y2=﹣x在同一平面坐标系中的图象可能是( )
A.B. C.D.
6.如图,将点P(﹣1,3)向右平移n个单位后落在直线y=2x﹣1上的点P′处,则n等于( )
A.2 B.2.5 C.3 D.4
7.已知点A(﹣1,y1),点B(2,y2)在函数y=﹣3x+2的图象上,那么y1与y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
8.在平面直角坐标系中,已知点和点,当直线为常数与线段AB有交点时,k的取值范围为
A. 或 B.
C. 或 D. 或
9.如图,直线经过点,当时,则x的取值范围为
A. B. C. D.
10.如图1,在平面直角坐标系中, ABCD在第一象限,且轴.直线从原点O出发沿x轴正方向平移,在平移过程中,直线被 ABCD截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 ABCD的面积为
A. 3 B. C. 6 D.
二、填空题(每题3分,共30分)
11.函数y=中,自变量x的取值范围是 .
12.若y=(k+1)x|k|+m+4是一次函数,则k= .
13.写出一个过点(0,0)且函数值y随自变量x的增大而减小的一次函数关系式 .
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.汽车的剩余油量y(L)随着行驶的距离x(km)的变化而变化,若一辆车y与x之间的关系式为y=-0.08x,则y随x的增大而____________.
18.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费(元与用水量(吨之间的函数关系如图所示.按上述分段收费标准,小明家三、四月份分别交水费29元和18元,则四月份比三月份节约用水__吨.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知y=y1+y2,其中y1与x成正比例,y2与x﹣2成正比例.当x=﹣1时,y=2;当x=3时,y=﹣2.求y与x的函数关系式.
20.已知y是x的一次函数,且当x=0时,y=﹣4;且图象通过点(1,﹣2)
(1)求这个一次函数的解析式;
(2)判断点(a,2a﹣4)是否在该函数图象上,并说明理由.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.如图,已知长方形ABCD中,AB=CD=16,BC=DA=24,E为CD边的中点,P为长方形ABCD边上的动点,动点P以4个单位/秒的速度从A出发,沿着A→B→C→E运动到E点停止,设点P运动的时间为t秒,△APE的面积为y.
(1)求当t=2时,y的值是 ;当t=6时,y的值是 .
(2)点P运动过程中,求出y与t之间的关系式;
24.商丘市梁园区紧紧围绕十九大报告提出的阶段性目标任务,深化农业供给侧结构性改革,调整种植结构,深入进行了四大结构调整,分别是:水池铺乡的辣椒产业、刘口乡的杂果基地,孙福集乡的山药、莲藕产业,双八镇的草莓产业.目前,这四种产业享誉省内外.
某外地客商慕名来商丘考查,他准备购入山药和草莓进行试销,经市场调查,若购进山药和草莓各2箱共花费170元,购进山药3箱和草莓4箱共花费300元.
(1)求购进山药和草莓的单价;
(2)若该客商购进了山药和草莓共1000箱,其中山药销售单价为60元,草莓的销售单价为70元.设购进山药x箱,获得总利润为y元.
①求y关于x的函数关系式;
②由于草莓的保鲜期较短,该客商购进草莓箱数不超过山药箱数的,要使销售这批山药和草莓的利润最大,请你帮该客商设计一个进货方案,并求出其所获利润的最大值.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A A C D D A C B C A
二、填空题(每题3分,共24分)
11.
12.平行
13. y=3x
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:根据题意设y1=k1x,y2=k2(x﹣2),即y=y1+y2=k1x+k2(x﹣2),
将x=﹣1时,y=2;x=3时,y=﹣2分别代入得:,
解得:k1=﹣,k2=﹣,
则y=﹣x﹣(x﹣2)=﹣x+1.
即y与x的函数关系式为y=﹣x+1.
20.解:(1)设这个一次函数的解析式为y=kx+b(k≠0),
将(0,﹣4),(1,﹣2)代入y=kx+b,得:,
解得:.
∴这个一次函数的解析式为y=2x﹣4.
(2)点(a,2a﹣4)在该函数图象上,理由如下:
∵当x=a时,y=2a﹣4,
∴点(a,2a﹣4)在函数图象上.
21.①5元;②0.5元;③45千克
22.①当0
②2.4元;6.4元
23.解:(1)长方形ABCD中,AB=CD=16,BC=DA=24,AD∥BC,∠BAD=∠B=∠C=∠D=90°,
∵P以4个单位/秒的速度从A出发,沿着A→B→C→E运动到E点停止,
∴当t=2时,则AP=4×2=8=AB,
即P为AB的中点,
∵E为CD边的中点,
∴四边形APED是矩形(如图1所示)
∴CE=DE=8,∠APE=∠B=90°,PE⊥AB,PE=BC=24
∴△APE的面积为;
当t=6时(如图2所示),
BP=6×4﹣AB=24﹣16=8,
∴PC=BC﹣BP﹣16
∴△APE的面积为;
故答案为:96;160;
(2)①当P在AB上时(如图1),
即0≤t≤4时,
此时,AP=4t,
∴△APE的面积为y=4t×24=48t,
②当点P在BC上时(如图2)
即4<t≤10,
此时BP=4t﹣16,
则PC=24﹣(4t﹣16)=40﹣4t
.
所以y与之间的关系式为y=﹣16t+256
③当P在CD上时(如图3)
即10<t≤12,
PE=48﹣4t,
∴△APE的面积为y=48﹣4t)×24=﹣48t+576.
24.解:(1)设购进每箱山药的单价为x元,购进每箱草莓的单价为y元,
根据题意得,
解得,
答:每箱山药的单价为40元,每箱草莓的单价为45元;
(2)①由题意可得,
y=(60﹣40)x+(70﹣45)(1000﹣x)=﹣5x+25000;
②由题意可得,
,
解得:x≥750,
又y=﹣5x+25000,k=﹣5<0,
∴y随x的增大而减小,
∴当x=750时,y达到最大值,即最大利润y=﹣5×750+25000=21250(元),
此时1000﹣x=1000﹣750=250(箱),
答:购进山药750箱,草莓250箱时所获利润最大,利润最大为21250元.
数学试卷 第19页(共22页) ( 数学试卷 第20页(共22页)
