第三单元圆柱与圆锥(单元测试)-2023-2024学年六年级下册数学人教版(含答案)
文档属性
| 名称 | 第三单元圆柱与圆锥(单元测试)-2023-2024学年六年级下册数学人教版(含答案) | 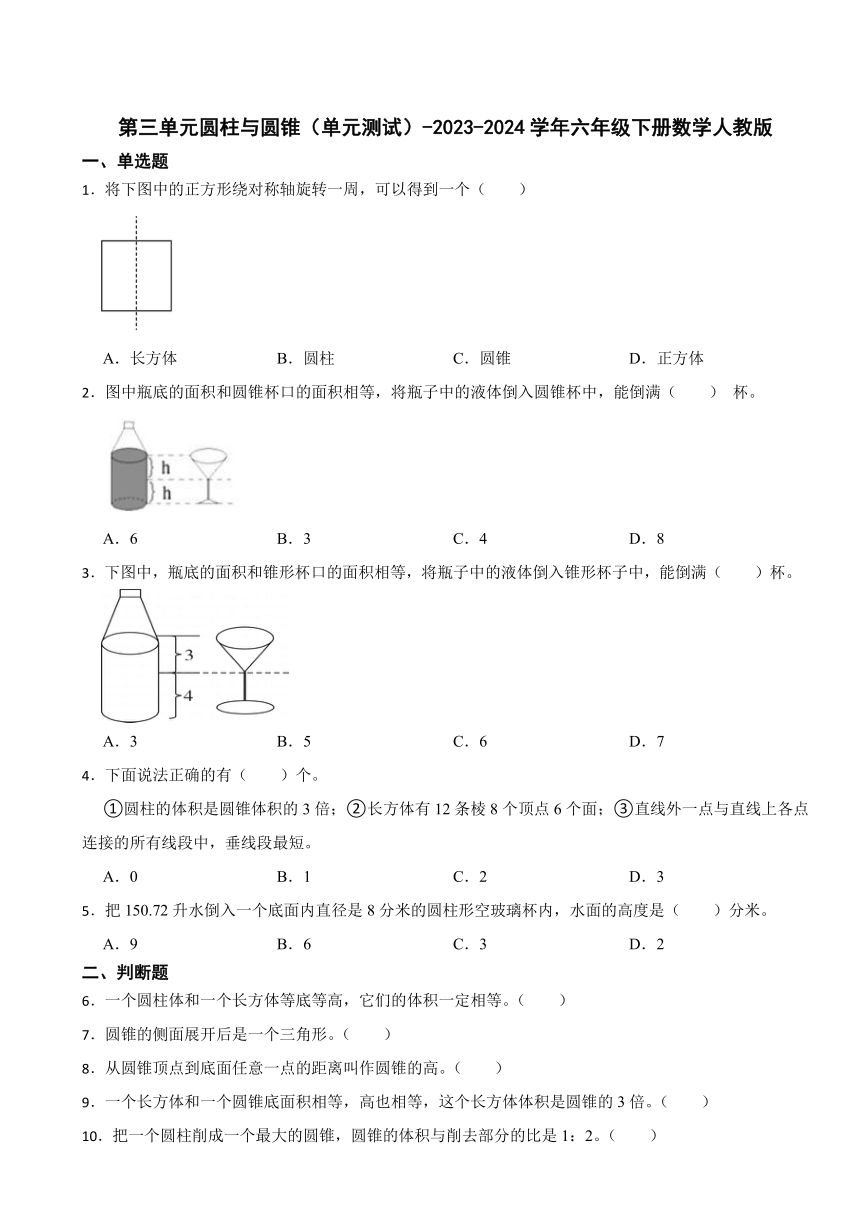 | |
| 格式 | docx | ||
| 文件大小 | 111.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 14:34:33 | ||
图片预览


文档简介
第三单元圆柱与圆锥(单元测试)-2023-2024学年六年级下册数学人教版
一、单选题
1.将下图中的正方形绕对称轴旋转一周,可以得到一个( )
A.长方体 B.圆柱 C.圆锥 D.正方体
2.图中瓶底的面积和圆锥杯口的面积相等,将瓶子中的液体倒入圆锥杯中,能倒满( ) 杯。
A.6 B.3 C.4 D.8
3.下图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子中,能倒满( )杯。
A.3 B.5 C.6 D.7
4.下面说法正确的有( )个。
①圆柱的体积是圆锥体积的3倍;②长方体有12条棱8个顶点6个面;③直线外一点与直线上各点连接的所有线段中,垂线段最短。
A.0 B.1 C.2 D.3
5.把150.72升水倒入一个底面内直径是8分米的圆柱形空玻璃杯内,水面的高度是( )分米。
A.9 B.6 C.3 D.2
二、判断题
6.一个圆柱体和一个长方体等底等高,它们的体积一定相等。( )
7.圆锥的侧面展开后是一个三角形。( )
8.从圆锥顶点到底面任意一点的距离叫作圆锥的高。( )
9.一个长方体和一个圆锥底面积相等,高也相等,这个长方体体积是圆锥的3倍。( )
10.把一个圆柱削成一个最大的圆锥,圆锥的体积与削去部分的比是1:2。( )
三、填空题
11.一个盛满水的圆锥形容器,水深21厘米,将水全部倒入和它等底等高的圆柱形容器里,水深是 厘米。
12.将一个圆柱的底面平均分成若干等份,切开后拼成一个近似的长方体(如图所示),长方体的长相当于圆柱体的 , 长方体的宽相当于圆柱体的 。
13.一个圆柱和一个圆锥的体积之比是8:3,圆柱的底面半径等于圆锥的底面直径。若圆锥的高是36dm,则圆柱的高是 dm。
14.一个圆锥形沙堆量得底面周长是12.56米,高1.5米,这个沙堆的体积是 立方米。
15.一根圆柱形木料,长1.5米,把它平均锯成两个小圆柱后,表面积增加了0.6平方米,这根木料的体积是 立方米。
16.一个圆柱体和一个圆锥体等底等高,他们的体积和是72立方分米,圆锥的体积是 立方分米,圆柱体的体积是 立方分米.
17.一个圆柱和一个圆锥的底面积相等,体积也相等,已知圆柱的高是6厘米,那么圆锥的高是 厘米。
四、解答题
18.有一条泥泞小路,李叔叔运来了一堆沙准备铺路。这堆沙堆成圆锥形,占地面积是9m2,高1.6m。把这堆沙铺在这条宽4m的泥泞小路上,平均铺5cm厚,可以铺多长?
19.矩形ABCD的边AB=2cm,AD=4cm,分别以AB、AD为轴旋转一周得两个不同的圆柱,哪个的表面积大?
20.一个圆柱形铁皮水桶(无盖),底面直径是8dm,高12dm。做这个水桶大约要用多少铁皮?(结果保留整数)
21.用一块硬纸板制作一个无盖圆柱形的笔筒(接缝处忽略不计),底面直径是10厘米,高是10厘米。一共需要硬纸板多少平方厘米?
22.如图,有一个高为8cm、容积为50mL的圆柱形容器A,里面装满了水。现将长为16 cm的圆柱体B垂直放入水中,使B的底面和A的底面接触,这时一部分水从容器中溢出。当把B从A中拿出后,A中水的高度为6 cm。求圆柱体B的体积。
23.分别绕AB和AC边旋转得到的圆锥体积相差多少.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】正确
7.【答案】错误
8.【答案】错误
9.【答案】正确
10.【答案】正确
11.【答案】7
12.【答案】底面周长的一半;底面半径
13.【答案】8
14.【答案】6.28
15.【答案】0.45
16.【答案】18;54
17.【答案】18
18.【答案】解:5厘米=0.05米
(9×1.6×)÷(4×0.05)
=(14.4×)÷0.2
=4.8÷0.2
=24(米)
答:可以铺24米。
19.【答案】解:以AB为轴,AD为底面半径时,底面积是最大的,所以AB为轴的表面积大.
20.【答案】解:3.14×8×12+3.14×42
=301.44+50.24
=351.68
≈352(平方分米)
答:大约要用352平方分米。
21.【答案】解:3.14×10×10+3.14×(10÷2) =392.5(平方厘米)
答:一共需要硬纸板392.5平方厘米。
22.【答案】解:50mL=50cm3
(8-6)÷8=2÷4=
50××2=12.5×2=25( cm3)
答:圆柱体B的体积是25立方厘米。
23.【答案】解: ×3.14×42×3﹣ ×3.14×32×4= ×3.14×16×3- ×3.14×9×4=50.24﹣37.68=12.56(立方厘米)答:得到的圆锥的体积相差12.56立方厘米。
一、单选题
1.将下图中的正方形绕对称轴旋转一周,可以得到一个( )
A.长方体 B.圆柱 C.圆锥 D.正方体
2.图中瓶底的面积和圆锥杯口的面积相等,将瓶子中的液体倒入圆锥杯中,能倒满( ) 杯。
A.6 B.3 C.4 D.8
3.下图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子中,能倒满( )杯。
A.3 B.5 C.6 D.7
4.下面说法正确的有( )个。
①圆柱的体积是圆锥体积的3倍;②长方体有12条棱8个顶点6个面;③直线外一点与直线上各点连接的所有线段中,垂线段最短。
A.0 B.1 C.2 D.3
5.把150.72升水倒入一个底面内直径是8分米的圆柱形空玻璃杯内,水面的高度是( )分米。
A.9 B.6 C.3 D.2
二、判断题
6.一个圆柱体和一个长方体等底等高,它们的体积一定相等。( )
7.圆锥的侧面展开后是一个三角形。( )
8.从圆锥顶点到底面任意一点的距离叫作圆锥的高。( )
9.一个长方体和一个圆锥底面积相等,高也相等,这个长方体体积是圆锥的3倍。( )
10.把一个圆柱削成一个最大的圆锥,圆锥的体积与削去部分的比是1:2。( )
三、填空题
11.一个盛满水的圆锥形容器,水深21厘米,将水全部倒入和它等底等高的圆柱形容器里,水深是 厘米。
12.将一个圆柱的底面平均分成若干等份,切开后拼成一个近似的长方体(如图所示),长方体的长相当于圆柱体的 , 长方体的宽相当于圆柱体的 。
13.一个圆柱和一个圆锥的体积之比是8:3,圆柱的底面半径等于圆锥的底面直径。若圆锥的高是36dm,则圆柱的高是 dm。
14.一个圆锥形沙堆量得底面周长是12.56米,高1.5米,这个沙堆的体积是 立方米。
15.一根圆柱形木料,长1.5米,把它平均锯成两个小圆柱后,表面积增加了0.6平方米,这根木料的体积是 立方米。
16.一个圆柱体和一个圆锥体等底等高,他们的体积和是72立方分米,圆锥的体积是 立方分米,圆柱体的体积是 立方分米.
17.一个圆柱和一个圆锥的底面积相等,体积也相等,已知圆柱的高是6厘米,那么圆锥的高是 厘米。
四、解答题
18.有一条泥泞小路,李叔叔运来了一堆沙准备铺路。这堆沙堆成圆锥形,占地面积是9m2,高1.6m。把这堆沙铺在这条宽4m的泥泞小路上,平均铺5cm厚,可以铺多长?
19.矩形ABCD的边AB=2cm,AD=4cm,分别以AB、AD为轴旋转一周得两个不同的圆柱,哪个的表面积大?
20.一个圆柱形铁皮水桶(无盖),底面直径是8dm,高12dm。做这个水桶大约要用多少铁皮?(结果保留整数)
21.用一块硬纸板制作一个无盖圆柱形的笔筒(接缝处忽略不计),底面直径是10厘米,高是10厘米。一共需要硬纸板多少平方厘米?
22.如图,有一个高为8cm、容积为50mL的圆柱形容器A,里面装满了水。现将长为16 cm的圆柱体B垂直放入水中,使B的底面和A的底面接触,这时一部分水从容器中溢出。当把B从A中拿出后,A中水的高度为6 cm。求圆柱体B的体积。
23.分别绕AB和AC边旋转得到的圆锥体积相差多少.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】正确
7.【答案】错误
8.【答案】错误
9.【答案】正确
10.【答案】正确
11.【答案】7
12.【答案】底面周长的一半;底面半径
13.【答案】8
14.【答案】6.28
15.【答案】0.45
16.【答案】18;54
17.【答案】18
18.【答案】解:5厘米=0.05米
(9×1.6×)÷(4×0.05)
=(14.4×)÷0.2
=4.8÷0.2
=24(米)
答:可以铺24米。
19.【答案】解:以AB为轴,AD为底面半径时,底面积是最大的,所以AB为轴的表面积大.
20.【答案】解:3.14×8×12+3.14×42
=301.44+50.24
=351.68
≈352(平方分米)
答:大约要用352平方分米。
21.【答案】解:3.14×10×10+3.14×(10÷2) =392.5(平方厘米)
答:一共需要硬纸板392.5平方厘米。
22.【答案】解:50mL=50cm3
(8-6)÷8=2÷4=
50××2=12.5×2=25( cm3)
答:圆柱体B的体积是25立方厘米。
23.【答案】解: ×3.14×42×3﹣ ×3.14×32×4= ×3.14×16×3- ×3.14×9×4=50.24﹣37.68=12.56(立方厘米)答:得到的圆锥的体积相差12.56立方厘米。
