第19章《 一次函数 》单元同步检测试题(含答案)
文档属性
| 名称 | 第19章《 一次函数 》单元同步检测试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 17:01:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.已知函数是正比例函数,且图像在第二、四象限内,则的值是( )
A.2 B. C.4 D.
2.已知点 , 都在直线 上,则, 的值的大小关系是( )
A. B. C. D.不能确定
3.下列给出的四个点中,在直线的是( )
A. B. C. D.
4.如图,某正比例函数的图象过点M(﹣2,1),则此正比例函数表达式为( )
A.y=﹣x B.y=x C.y=﹣2x D.y=2x
5.某地海拔高度h与温度T的关系可用T=21﹣6h来表示(其中温度单位为℃,高度单位为千米),则该地区海拔高度为2000米的山顶上的温度是( )
A.15℃ B.3℃ C.﹣1179℃ D.9℃
6.若正比例函数y=kx(k≠0)的图象经过点(1,﹣2),则其表达式为( )
A.y=x B.y=﹣x C.y=2x D.y=﹣2x
7.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.如果每盒羽毛球有20个,每盒售价为24元,那么羽毛球的售价(元)与羽毛球个数(个)之间的关系式为( )
A. B. C. D.
9. 已知两地相距3千米,小黄从地到地,平均速度为4千米/小时,若用表示行走的时间(小时),表示余下的路程(千米),则关于的函数解析式是
A. B.
C. D.
10. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
二、填空题(每题3分,共30分)
11.已知点,都在直线上,则,大小关系是:__________.
12.若个直三棱柱的面的个数为个,则关于的函数表达式为__________.
13.已知点P(x,y)是一次函数y=x+4图象上的任意一点,连接原点O与点P,则线段OP长度的最小值为_____.
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
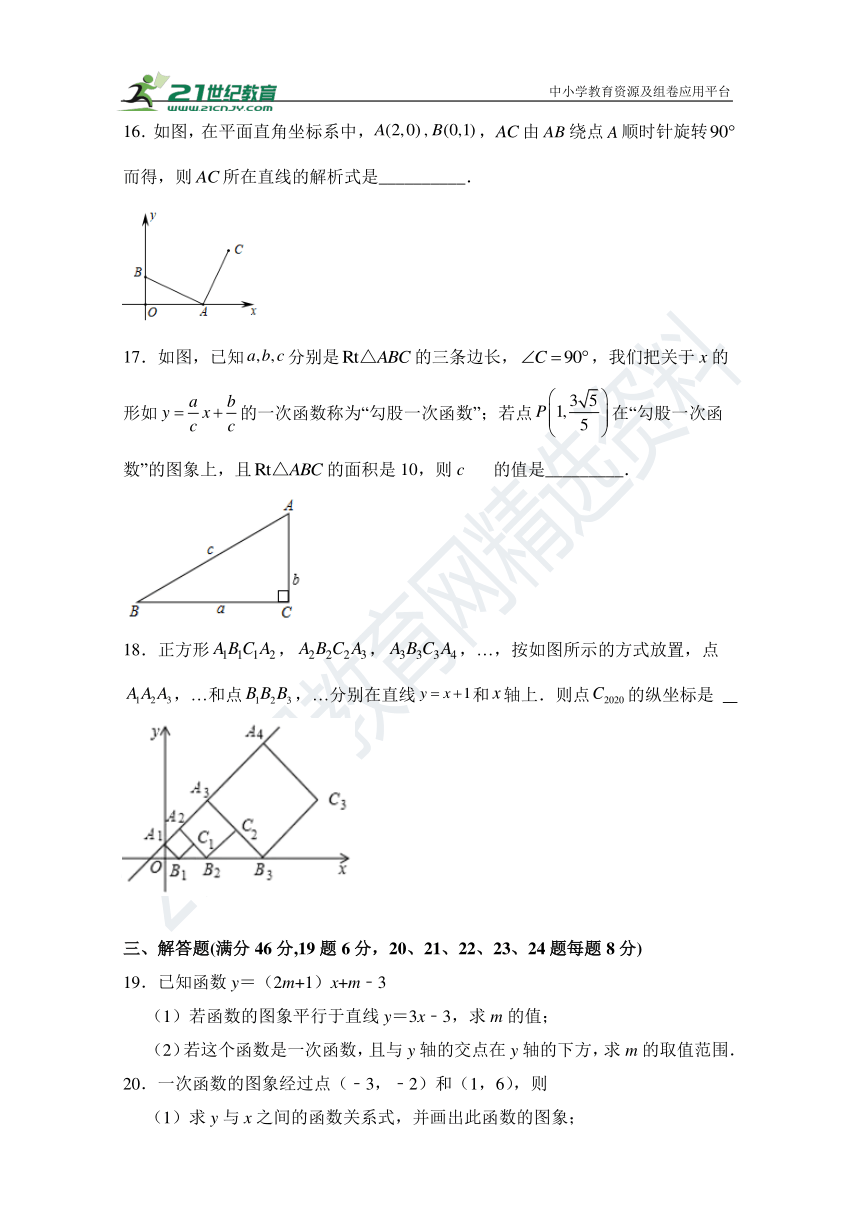
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.如图,已知分别是的三条边长,,我们把关于x的形如的一次函数称为“勾股一次函数”;若点在“勾股一次函数”的图象上,且的面积是10,则c的值是_________.
18.正方形,,,…,按如图所示的方式放置,点,…和点,…分别在直线和轴上.则点的纵坐标是
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知函数y=(2m+1)x+m﹣3
(1)若函数的图象平行于直线y=3x﹣3,求m的值;
(2)若这个函数是一次函数,且与y轴的交点在y轴的下方,求m的取值范围.
20.一次函数的图象经过点(﹣3,﹣2)和(1,6),则
(1)求y与x之间的函数关系式,并画出此函数的图象;
(2)若函数的图象过点(m,3m),试求m的值
(3)如果y的取值为﹣1≤y≤2,求x的取值范围.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.为了落实党的“精准扶贫”政策,A,B两城决定向C,D两乡运送肥料以支持农村生产.已知A,B两城分别有肥料210吨和290吨,从A城往C,D两乡运送肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运送肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)设从A城运往C乡的肥料有x吨.
①用含x的代数式完成下表:
C乡(吨) D乡(吨)
A城 x
B城
②设总运费为y元,写出y与x的函数关系式,并求出最少总运费.
(2)由于更换车型,使A城运往C乡的运费每吨减少a(024.如图8①,在平面直角坐标系中,直线AB分别交x轴、y轴于点A(a,0)、点B(0,b),且a,b满足a2+4a+4+|2a+b|=0.
(1)a= ,b= .
(2)点P在直线AB的右侧,且∠APB=45°.
①若点P在x轴上,则点P的坐标为 ;
②若△ABP为直角三角形,求点P的坐标.
(3)如图②,在(2)的条件下,∠BAP=90°且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接MN.求证:∠1=∠2.(提示:过点P作PH⊥AP交x轴于点H)
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D D D A C B C A
二、填空题(每题3分,共24分)
11.
12.平行
13. y=3x
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知函数y=(2m+1)x+m﹣3
(1)若函数的图象平行于直线y=3x﹣3,求m的值;
(2)若这个函数是一次函数,且与y轴的交点在y轴的下方,求m的取值范围.
【分析】(1)根据直线y=(2m+1)x+m﹣3与直线y=3x﹣3平行,即可得出关于m的一元一次方程及一元一次不等式,解之即可得出结论;
(2)根据一次函数的定义及一次函数图象上点的坐标特征,即可得出关于m的一元一次不等式组,解不等式组即可得出结论.
【解答】解:(1)∵直线y=(2m+1)x+m﹣3与直线y=3x﹣3平行,
∴,
解得:m=1.
(2)∵函数y=(2m+1)x+m﹣3是一次函数,且与y轴的交点在y轴的下方,
∴,
∴m<3且m≠﹣.
20.一次函数的图象经过点(﹣3,﹣2)和(1,6),则
(1)求y与x之间的函数关系式,并画出此函数的图象;
(2)若函数的图象过点(m,3m),试求m的值
(3)如果y的取值为﹣1≤y≤2,求x的取值范围.
【分析】(1)设一次函数的关系式为y=kx+b(k≠0),再把点(﹣3,﹣2)和(1,6)代入即可求出kb的值,进而得出其关系式;在坐标系内描出两点,画出函数图象即可;
(2)把点(m,3m)代入(1)中所求函数关系式,求出m的值即可;
(3)根据y的取值为﹣1≤y≤2得出关于x的不等式组,求出x的取值范围即可.
【解答】解:(1)设一次函数的关系式为y=kx+b(k≠0),
∵点(﹣3,﹣2)和(1,6)在一次函数的图象上,
∴,解得,
∴此一次函数的解析式为:y=2x+4.
其图象为:
(2)∵函数的图象过点(m,3m),
∴2m+4=3m,解得m=4;
(3)∵一次函数的解析式为:y=2x+4,
∴y的取值为﹣1≤y≤2时,即,解得﹣≤x≤﹣1.
21.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23.解:(1)①由从A城运往C乡的肥料有x吨,可得从A城运往D乡的肥料为(210-x)吨;从B城运往C乡的肥料为(240-x)吨,从B城运往D乡的肥料为(50+x)吨.
故答案为210-x,240-x,50+x.
②y=20x+25(210-x)+15(240-x)+24(x+50)=4x+10050.
因为y=4x+10050是一次函数,k=4>0,
所以y随x的增大而增大.
因为x≥0,所以当x=0时,总运费最少,最少总运费是10050元.
(2)y=(20-a)x+25(210-x)+15(240-x)+24(x+50)=(4-a)x+10050.
当00,
∴当x=0时,总运费最少是10050元;
当4∵4-a<0,
∴当x最大时,总运费最少.即当x=210时,总运费最少.
当a=4时,不管A城运往C乡的肥料有多少吨(不超过210吨),总运费都是10050元.
综上所述,当024.解:(1)-2 4
(2)①(4,0)
②若∠BAP=90°,过点P作PG⊥x轴于点G,如图(a)所示.
∵∠BAP=∠AOB=90°,
∴∠GAP+∠BAG=90°,∠ABO+∠BAG=90°,
∴∠ABO=∠GAP.
∵∠APB=45°,∠BAP=90°,
∴AP=AB.
又∵∠AOB=∠AGP=90°,
∴△AOB≌△PGA(AAS),
∴PG=AO=2,AG=OB=4,
∴OG=AG-AO=2,
故点P的坐标为(2,-2).
若∠ABP=90°,
同理可得点P的坐标为(4,2).
故点P的坐标为(2,-2)或(4,2).
(3)证明:过点P作PH⊥AP交x轴于点H,过点P分别作PE⊥y轴,PF⊥x轴,垂足分别为E,F,如图(b).
由(2)知,PE=PF=2.
∵∠MPN=45°,
∴∠MPE+∠NPF=∠EPF-∠MPN=90°-45°=45°,
∠HPF+∠NPF=∠MPH-∠MPN=90°-45°=45°,
∴∠MPE=∠HPF.
又∵∠HFP=∠MEP=90°,
∴△MEP≌△HFP,
∴∠2=∠NHP,MP=HP.
又∵∠HPN=∠HPF+∠NPF=45°=∠MPN,PN=PN,
∴△MNP≌△HNP,
∴∠1=∠NHP,
∴∠1=∠2.
数学试卷 第3页(共20页) ( 数学试卷 第4页(共20页)
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.已知函数是正比例函数,且图像在第二、四象限内,则的值是( )
A.2 B. C.4 D.
2.已知点 , 都在直线 上,则, 的值的大小关系是( )
A. B. C. D.不能确定
3.下列给出的四个点中,在直线的是( )
A. B. C. D.
4.如图,某正比例函数的图象过点M(﹣2,1),则此正比例函数表达式为( )
A.y=﹣x B.y=x C.y=﹣2x D.y=2x
5.某地海拔高度h与温度T的关系可用T=21﹣6h来表示(其中温度单位为℃,高度单位为千米),则该地区海拔高度为2000米的山顶上的温度是( )
A.15℃ B.3℃ C.﹣1179℃ D.9℃
6.若正比例函数y=kx(k≠0)的图象经过点(1,﹣2),则其表达式为( )
A.y=x B.y=﹣x C.y=2x D.y=﹣2x
7.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.如果每盒羽毛球有20个,每盒售价为24元,那么羽毛球的售价(元)与羽毛球个数(个)之间的关系式为( )
A. B. C. D.
9. 已知两地相距3千米,小黄从地到地,平均速度为4千米/小时,若用表示行走的时间(小时),表示余下的路程(千米),则关于的函数解析式是
A. B.
C. D.
10. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
二、填空题(每题3分,共30分)
11.已知点,都在直线上,则,大小关系是:__________.
12.若个直三棱柱的面的个数为个,则关于的函数表达式为__________.
13.已知点P(x,y)是一次函数y=x+4图象上的任意一点,连接原点O与点P,则线段OP长度的最小值为_____.
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.如图,已知分别是的三条边长,,我们把关于x的形如的一次函数称为“勾股一次函数”;若点在“勾股一次函数”的图象上,且的面积是10,则c的值是_________.
18.正方形,,,…,按如图所示的方式放置,点,…和点,…分别在直线和轴上.则点的纵坐标是
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知函数y=(2m+1)x+m﹣3
(1)若函数的图象平行于直线y=3x﹣3,求m的值;
(2)若这个函数是一次函数,且与y轴的交点在y轴的下方,求m的取值范围.
20.一次函数的图象经过点(﹣3,﹣2)和(1,6),则
(1)求y与x之间的函数关系式,并画出此函数的图象;
(2)若函数的图象过点(m,3m),试求m的值
(3)如果y的取值为﹣1≤y≤2,求x的取值范围.
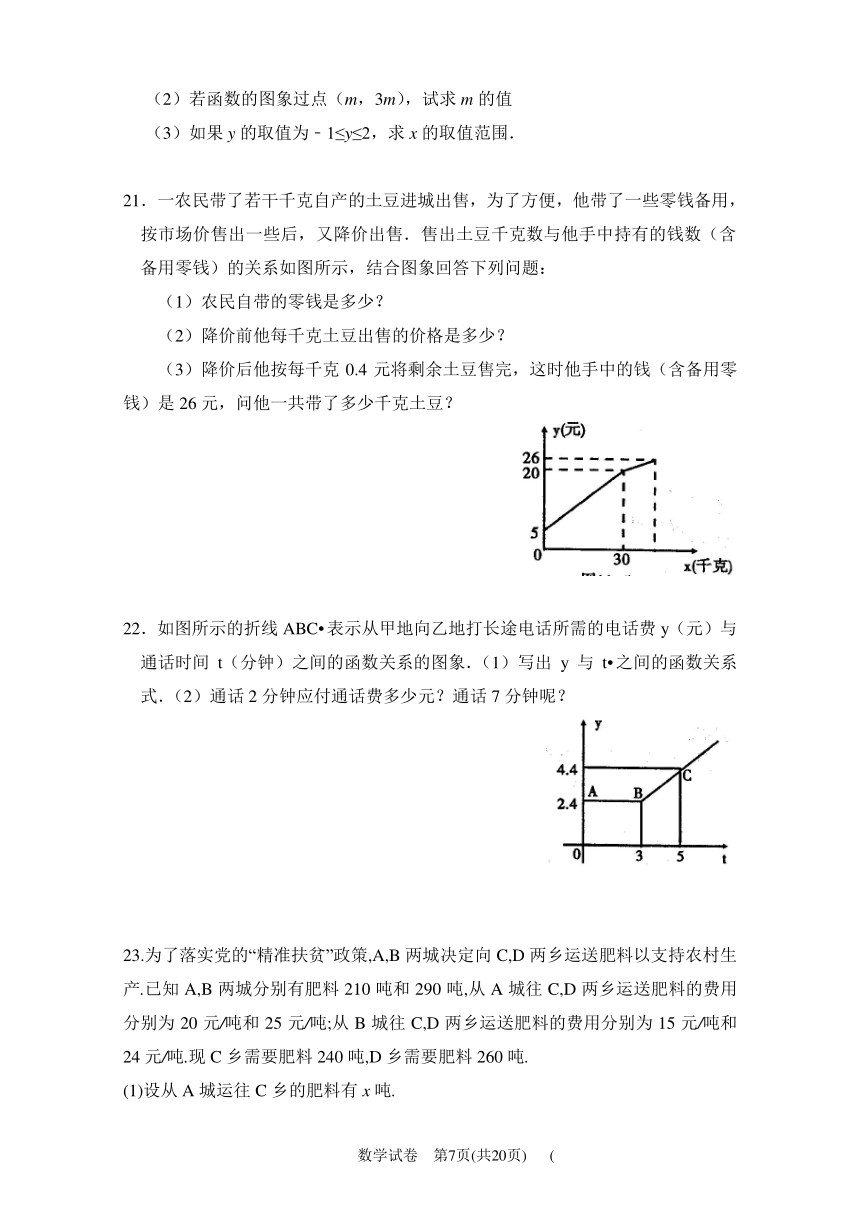
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.为了落实党的“精准扶贫”政策,A,B两城决定向C,D两乡运送肥料以支持农村生产.已知A,B两城分别有肥料210吨和290吨,从A城往C,D两乡运送肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运送肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)设从A城运往C乡的肥料有x吨.
①用含x的代数式完成下表:
C乡(吨) D乡(吨)
A城 x
B城
②设总运费为y元,写出y与x的函数关系式,并求出最少总运费.
(2)由于更换车型,使A城运往C乡的运费每吨减少a(0
(1)a= ,b= .
(2)点P在直线AB的右侧,且∠APB=45°.
①若点P在x轴上,则点P的坐标为 ;
②若△ABP为直角三角形,求点P的坐标.
(3)如图②,在(2)的条件下,∠BAP=90°且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接MN.求证:∠1=∠2.(提示:过点P作PH⊥AP交x轴于点H)
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D D D A C B C A
二、填空题(每题3分,共24分)
11.
12.平行
13. y=3x
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知函数y=(2m+1)x+m﹣3
(1)若函数的图象平行于直线y=3x﹣3,求m的值;
(2)若这个函数是一次函数,且与y轴的交点在y轴的下方,求m的取值范围.
【分析】(1)根据直线y=(2m+1)x+m﹣3与直线y=3x﹣3平行,即可得出关于m的一元一次方程及一元一次不等式,解之即可得出结论;
(2)根据一次函数的定义及一次函数图象上点的坐标特征,即可得出关于m的一元一次不等式组,解不等式组即可得出结论.
【解答】解:(1)∵直线y=(2m+1)x+m﹣3与直线y=3x﹣3平行,
∴,
解得:m=1.
(2)∵函数y=(2m+1)x+m﹣3是一次函数,且与y轴的交点在y轴的下方,
∴,
∴m<3且m≠﹣.
20.一次函数的图象经过点(﹣3,﹣2)和(1,6),则
(1)求y与x之间的函数关系式,并画出此函数的图象;
(2)若函数的图象过点(m,3m),试求m的值
(3)如果y的取值为﹣1≤y≤2,求x的取值范围.
【分析】(1)设一次函数的关系式为y=kx+b(k≠0),再把点(﹣3,﹣2)和(1,6)代入即可求出kb的值,进而得出其关系式;在坐标系内描出两点,画出函数图象即可;
(2)把点(m,3m)代入(1)中所求函数关系式,求出m的值即可;
(3)根据y的取值为﹣1≤y≤2得出关于x的不等式组,求出x的取值范围即可.
【解答】解:(1)设一次函数的关系式为y=kx+b(k≠0),
∵点(﹣3,﹣2)和(1,6)在一次函数的图象上,
∴,解得,
∴此一次函数的解析式为:y=2x+4.
其图象为:
(2)∵函数的图象过点(m,3m),
∴2m+4=3m,解得m=4;
(3)∵一次函数的解析式为:y=2x+4,
∴y的取值为﹣1≤y≤2时,即,解得﹣≤x≤﹣1.
21.①5元;②0.5元;③45千克
22.①当0
②2.4元;6.4元
23.解:(1)①由从A城运往C乡的肥料有x吨,可得从A城运往D乡的肥料为(210-x)吨;从B城运往C乡的肥料为(240-x)吨,从B城运往D乡的肥料为(50+x)吨.
故答案为210-x,240-x,50+x.
②y=20x+25(210-x)+15(240-x)+24(x+50)=4x+10050.
因为y=4x+10050是一次函数,k=4>0,
所以y随x的增大而增大.
因为x≥0,所以当x=0时,总运费最少,最少总运费是10050元.
(2)y=(20-a)x+25(210-x)+15(240-x)+24(x+50)=(4-a)x+10050.
当0
∴当x=0时,总运费最少是10050元;
当4
∴当x最大时,总运费最少.即当x=210时,总运费最少.
当a=4时,不管A城运往C乡的肥料有多少吨(不超过210吨),总运费都是10050元.
综上所述,当0
(2)①(4,0)
②若∠BAP=90°,过点P作PG⊥x轴于点G,如图(a)所示.
∵∠BAP=∠AOB=90°,
∴∠GAP+∠BAG=90°,∠ABO+∠BAG=90°,
∴∠ABO=∠GAP.
∵∠APB=45°,∠BAP=90°,
∴AP=AB.
又∵∠AOB=∠AGP=90°,
∴△AOB≌△PGA(AAS),
∴PG=AO=2,AG=OB=4,
∴OG=AG-AO=2,
故点P的坐标为(2,-2).
若∠ABP=90°,
同理可得点P的坐标为(4,2).
故点P的坐标为(2,-2)或(4,2).
(3)证明:过点P作PH⊥AP交x轴于点H,过点P分别作PE⊥y轴,PF⊥x轴,垂足分别为E,F,如图(b).
由(2)知,PE=PF=2.
∵∠MPN=45°,
∴∠MPE+∠NPF=∠EPF-∠MPN=90°-45°=45°,
∠HPF+∠NPF=∠MPH-∠MPN=90°-45°=45°,
∴∠MPE=∠HPF.
又∵∠HFP=∠MEP=90°,
∴△MEP≌△HFP,
∴∠2=∠NHP,MP=HP.
又∵∠HPN=∠HPF+∠NPF=45°=∠MPN,PN=PN,
∴△MNP≌△HNP,
∴∠1=∠NHP,
∴∠1=∠2.
数学试卷 第3页(共20页) ( 数学试卷 第4页(共20页)
