沪教版七年级数学下册试题 14.2全等三角形(含解析)
文档属性
| 名称 | 沪教版七年级数学下册试题 14.2全等三角形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 17:04:54 | ||
图片预览


文档简介
第二节 全等三角形
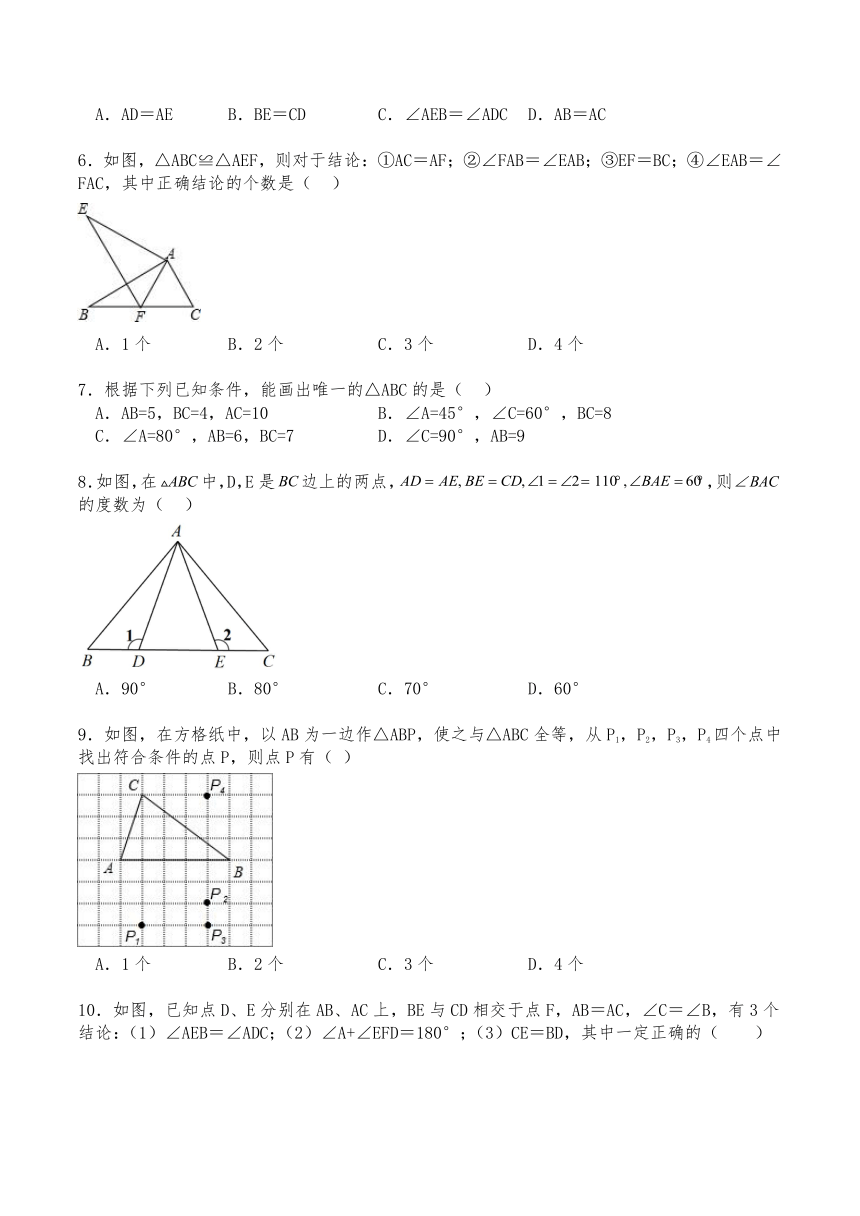
一、单选题
1.关于全等三角形,下列说法正确的是( )
A.大小相等的三角形是全等三角形
B.面积相等的三角形是全等三角形
C.三个角对应相等的三角形是全等三角形
D.两个三角形全等,它们的形状一定相同
2.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
3.如图,用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( )
A. B. C. D.
4.小刚把一块三角形玻璃打碎成了如图所示的三块,现要到玻璃店取配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
5.如图,已知∠B=∠C,补充下列条件后,不能判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.∠AEB=∠ADC D.AB=AC
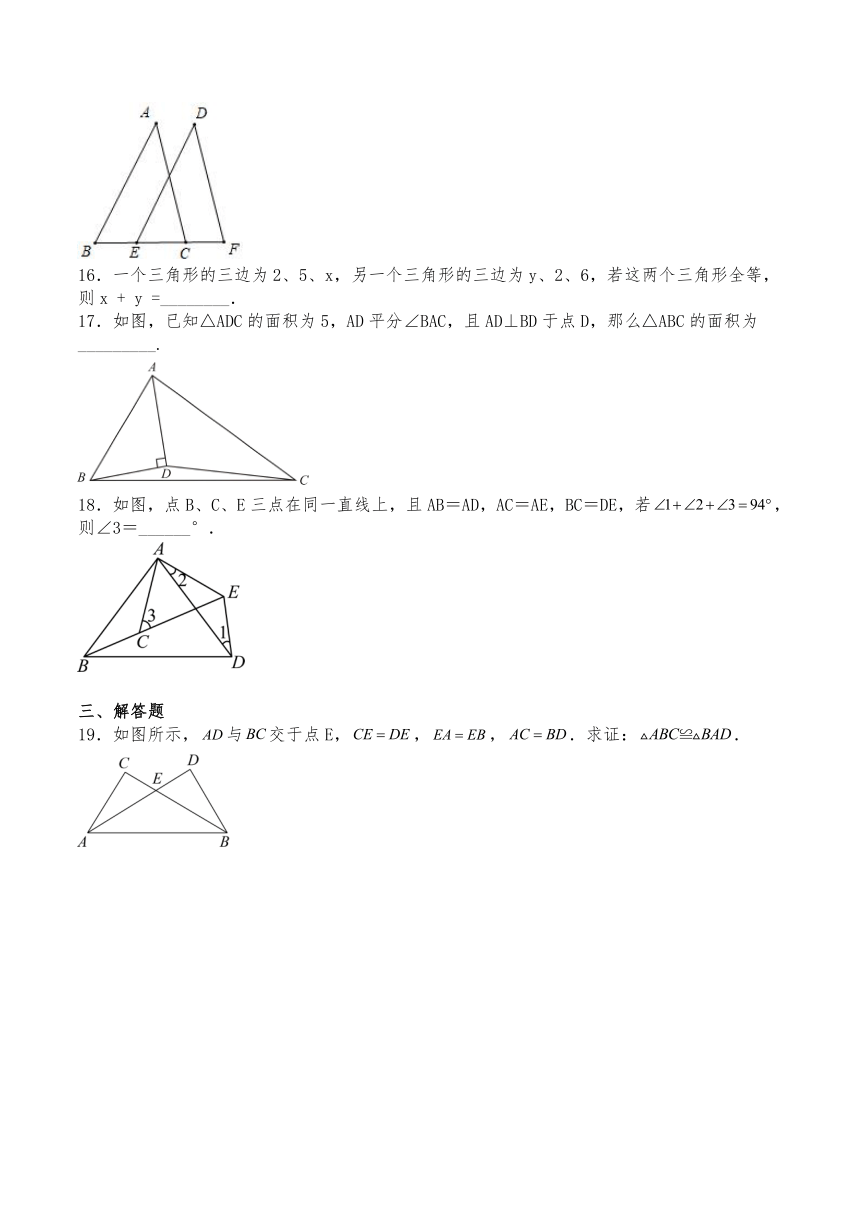
6.如图,△ABC≌△AEF,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
7.根据下列已知条件,能画出唯一的△ABC的是( )
A.AB=5,BC=4,AC=10 B.∠A=45°,∠C=60°,BC=8
C.∠A=80°,AB=6,BC=7 D.∠C=90°,AB=9
8.如图,在中,D,E是边上的两点,,则的度数为( )
A.90° B.80° C.70° D.60°
9.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
10.如图,已知点D、E分别在AB、AC上,BE与CD相交于点F,AB=AC,∠C=∠B,有3个结论:(1)∠AEB=∠ADC;(2)∠A+∠EFD=180°;(3)CE=BD,其中一定正确的( )
A.0个 B.1个 C.2个 D.3个
二、填空题
11.如图,在△ABC与△ACD中,AB∥CD,请添加一个条件:______,使△ABC≌△CDA.
12.如图,有两根钢条、,在中点处以小转轴连在一起做成工具(卡错),可测量工件内槽的宽.如果测量,那么工件内槽的宽______cm.
13.如图,在△ABC和△BAD中,因为AB=BA,∠ABC=∠BAD,_____=_____,根据“SAS”可以得到△ABC≌△BAD.
14.如图,已知△ABC≌△ABD,其中AC、BC的对应边分别是AD、BD,∠C=60°,∠ABC=80°,那么∠CAD=___度.
15.如图,点B、E、C、F在同一条直线上,AB∥DE,AB=DE,∠A=∠D,BF=10,BC=6,则EC=_____.
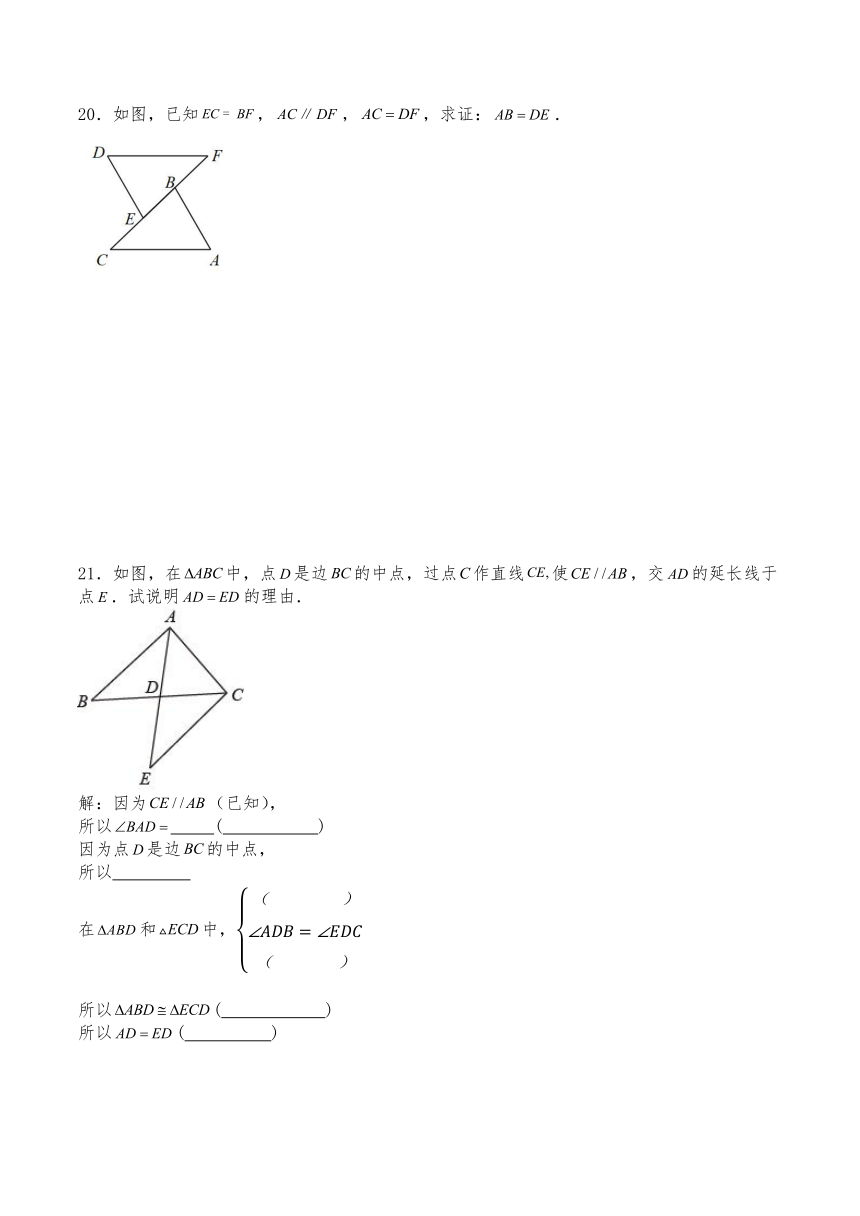
16.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x + y =________.
17.如图,已知△ADC的面积为5,AD平分∠BAC,且AD⊥BD于点D,那么△ABC的面积为_________.
18.如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若,则∠3=______°.
三、解答题
19.如图所示,与交于点E,,,.求证:.
20.如图,已知,,,求证:.
21.如图,在中,点是边的中点,过点作直线使,交的延长线于点.试说明的理由.
解:因为(已知),
所以 ( )
因为点是边的中点,
所以
在和中,
所以( )
所以( )
22.如图,已知E、F是BD上的两点,BE=DF,AE=CF,AE∥CF,请填写AD∥BC的理由.
解:因为AE∥CF(已知),
所以∠AED= (两直线平行,内错角相等).
因为BE=DF(已知),
所以BE+EF=DF+EF( ),
即BF=DE.
在△ADE与△CBF中
,
所以△ADE≌△CBF( ).
得∠ADE=∠CBF( ).
所以AD∥BC( ).
23.已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.
(1)请说明△AOC≌△BOD的理由;
(2)请说明OM=ON的理由.
24. 如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长
25.如图,已知在△ABC中,AM是△ABC的中线,MP平分∠AMBA,MQ平分∠AMC,且BP⊥MP于点P,CQ⊥MQ于点Q.
(1)求证:MP⊥MQ;
(2)求证:△BMP≌△MCQ.
26.已知:中,,,D为直线BC上一动点,连接AD,在直线AC右侧作,且.
(1)如图1,当点D在线段BC上时,过点E作于H,连接DE,求证:;
(2)如图2,当点D在线段BC的延长线上时,连接BE交CA的延长线于点M.
求证:;
(3)当点D在射线CB上时,连接BE交直线AC于M,若,则的值为______.
答案
一、单选题
1.D
【分析】根据全等三角形的定义:能够完全重合的两个三角形,对各个选项进行判断即可.
【解析】解:A、大小相等的三角形,形状不一定相同,所以不一定完全重合,故该选项不符合题意;
B、面积相等的三角形,形状不一定相同,所以不一定完全重合,故该选项不符合题意;
C、三个角对应相等的三角形,边长不一定相等,所以不一定完全重合,故该选项不符合题意;
D、两个三角形全等,它们的形状一定相同,故该选项符合题意;
故选:D.
2.A
【分析】根据∠α是b、c边的夹角,然后写出即可.
【解析】解:∵两个三角形全等,
∴∠α的度数是72°.
故选:A.
3.A
【分析】利用全等三角形的判定方法判断即可.
【解析】解:由作法易得,,,
在和中,
,
,
∴,
故选:A.
4.C
【分析】根据三角形全等的条件进行判断即可.
【解析】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据来配一块一样的玻璃,应带③去.
故选:C.
5.C
【分析】根据全等三角形的判定定理逐个判断即可.A可利用AAS判定;B可利用AAS判定;C只有三个对应角相等,无法证明;D可利用ASA判定.
【解析】A.∵∠B=∠C,∠A=∠A,AE=AD,
∴△ABE≌△ACD(AAS),故该选项不符合题意;
B.∵∠A=∠A,∠B=∠C,BE=CD,
∴△ABE≌△ACD(AAS),故该选项不符合题意;
C.由题意可知只有∠A=∠A,∠B=∠C,∠AEB=∠ADC三个已知条件,
∴无法由三个角对应相等证明三角形全等,故该选项符合题意;
D.∵∠B=∠C,AB=AC,∠A=∠A,
∴△ABE≌△ACD(ASA),故该选项不符合题意;
故选C.
6.C
【分析】根据全等三角形的性质即可进行判断.
【解析】∵△ABC≌△AEF,
∴AC=AF,EF=BC,
故①③正确;
∵△ABC≌△AEF,
∴∠EAF=∠BAC,
∴∠EAF-∠BAF=∠BAC-∠BAF,
∴∠EAB=∠FAC,
故④正确;
∠FAB=∠EAB不一定相等,故②不符合题意;
综上:正确的有3个,
故选:C.
7.B
【分析】要满足唯一画出△ABC,就要求选项给出的条件符合三角形全等的判定方法,不符合判定方法的画出的图形不一样,也就是三角形不唯一,而各选项中只有C选项符合ASA,是满足题目要求的,于是答案可得.
【解析】解:A、因为AB+BC<AC,所以这三边不能构成三角形;
B、已知两角可得到第三个角的度数,已知一边,则可以根据ASA来画一个三角形;
C、因为∠A不是已知两边的夹角,无法确定其他角的度数与边的长度;
D、只有一个角和一个边无法根据此作出一个三角形.
故选:B.
8.B
【分析】先证明BD=CE,然后证明△ADB≌△AEC,∠ADE=∠AED=70°,得到∠BAD=∠CAE,根据三角形内角和定理求出∠DAE=40°,从而求出∠BAD的度数即可得到答案.
【解析】解:∵BE=CD,
∴BE-DE=CD-DE,即BD=CE,
∵∠1=∠2=110°,AD=AE,
∴△ADB≌△AEC(SAS),∠ADE=∠AED=70°,
∴∠BAD=∠CAE,∠DAE=180°-∠ADE-∠AED=40°,
∵∠BAE=60°,
∴∠BAD=∠CAE=20°,
∴∠BAC=80°,
故选B.
9.C
【解析】要使△ABP与△ABC全等,
必须使点P到AB的距离等于点C到AB的距离,
即3个单位长度,
所以点P的位置可以是P1,P,P4三个,
故选C.
10.C
【分析】(1)通过证得△AEB≌△ADC,即可证得结论;
(2)根据题意,只有在CD⊥AB,BE⊥AC时,∠A+∠EFD=180°才成立;
(3)根据全等三角形的性质即可证得AD=AE,进而即可证得结论.
【解析】解:(1)在△AEB和△ADC中,
,
∴△AEB≌△ADC(ASA),
∴∠AEB=∠ADC,
故(1)正确;
(2)∵∠EFD=∠CEF+∠C,
∴∠A+∠EFD=∠CEF+∠A+∠C=∠CEF+∠BDF,
∵∠AEB=∠ADC,
∴∠CEF=∠BDF,
若∠A+∠EFD=180°,则∠CEF=∠BDF=90°,
故只有在CD⊥AB,BE⊥AC时,∠A+∠EFD=180°才成立,
故(2)错误;
(3)∵△AEB≌△ADC,
∴AD=AE,
∵AB=AC,
∴CE=BD,
故(3)正确;
综上,3个结论中一定正确的是(1)(3)两个,
故选:C.
二、填空题
11.AB=CD(答案不唯一)
【分析】根据平行线的性质可得∠BAC=∠DCA,再添加AB=CD可利用SAS判定△ABC≌△CDA.
【解析】解:添加AB=CD,理由如下:
∵AB∥CD,
∴∠BAC=∠DCA,
在△ABC和△CDA中,,
∴△ABC≌△CDA(SAS),
故答案为:AB=CD(答案不唯一).
12.2
【分析】利用SAS证明,即可得到答案.
【解析】解:由题意得:在△BOD和△AOC中,
,
∴,
∴,
故答案为:2.
13. BC AD
【分析】因为夹∠ABC的两边分别为AB的BC,所以再加上BC=AD,得△ABC≌△BAD(SAS).
【解析】解:∵AB=BA,∠ABC=∠BAD,
∴再加上BC=AD,
∴△ABC≌△BAD(SAS).
故答案为:①BC;②AD.
14.80
【分析】根据三角形的内角和定理得到∠CAB=180°-∠C-∠ABC=40°,根据全等三角形的性质得到∠DAB=∠CAB=40°,于是得到结论.
【解析】解:∵∠C=60°,∠ABC=80°,
∴∠CAB=180°-∠C-∠ABC=180°-60°-80°=40°,
∵△ABC≌△ABD,
∴∠DAB=∠CAB=40°,
∴∠CAD=∠CAB+∠DAB=80°,
故答案为:80.
15.2
【分析】根据平行线的性质得出∠B=∠DEF,即可利用ASA证明△ABC≌△DEF,根据全等三角形的性质得出BC=EF=6,即可根据线段的和差得解.
【解析】解:∵AB∥DE,
∴∠B=∠DEF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴BC=EF,
∵BF=10,BC=6,
∴EF=6,CF=BF﹣BC=4,
∴EC=EF﹣CF=2,
故答案为:2.
16.11
【分析】根据全等三角形的性质求出x和y即可.
【解析】解:∵这两个三角形全等
∴x=6,y=5
∴x + y =11
故答案为11.
17.10
【分析】首先延长BD,交AC于点E,再根据“ASA”证明△ABD≌△AED,由S△ADE+S△CDE=S△ABD+S△BCD,可知S△ABC=2 S△ACD,可得答案.
【解析】延长BD,交AC于点E,
∵AD平分∠BAE,
∴∠BAD=∠EAD.
∵∠ADB=∠ADE,AD=AD,
∴△ABD≌△AED,
∴BD=DE,
∴S△BCD= S△CDE,
∴S△ADE+S△CDE=S△ABD+S△BCD=5,
∴S△ABC=2 S△ACD=10.
故答案为:10
18.47
【分析】根据“边边边”证明,再根据全等三角形的性质可得∠ABC=∠1,∠BAC=∠2,然后利用三角形的一个外角等于与它不相邻的两个内角和求出∠3=∠1+∠2,然后求解即可.
【解析】解:在△ABC和△ADE中,,
∴(SSS),
∴∠ABC=∠1,∠BAC=∠2,
∴∠3=∠ABC+∠BAC=∠1+∠2,
∵,
∴,
∴.
故答案为:47.
三、解答题
19.,,
,
即BC=AD,
在和中,
(SSS)
20.∵
∴,即
∵
∴
又∵
∴ △DEF≌△ABC(SAS)
∴.
21.解:因为(已知),
所以∠E(两直线平行,内错角相等)
因为点是边的中点,
所以BD=CD.
在和中,
(对顶角相等)
所以(AAS)
所以(全等三角形的对应边相等)
22.证明:因为AE∥CF(已知),
所以∠AED=∠CFB(两直线平行,内错角相等),
因为BE=DF(已知),
所以BE+EF=DF+EF(等式的性质),
即BF=DE.
在△ADE与△CBF中,
,
所以△ADE≌△CBF(SAS),
得∠ADE=∠CBF(全等三角形的对应角相等),
所以AD∥BC(内错角相等,两直线平行),
故答案为:∠CFB;等式的性质;AE=CF,DE=BF;SAS;全等三角形的对应角相等;内错角相等,两直线平行.
23.(1)∵∠AOB=∠BOC=∠COD,
∴∠AOC=∠BOD,
在△AOC与△BOD中,
,
∴△AOC≌△BOD;
(2)∵△AOC≌△BOD,
∴∠A=∠B,
在△AOM与△BON中,
,
∴△AOM≌△BON,
∴OM=ON.
24.(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
在△DBC和△ECA中,
∵,
∴△DBC≌△ECA(AAS).
∴AE=CD;
(2)解:∵△CDB≌△AEC,
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC=BC=AC,且AC=12cm.
∴BD=6cm.
25.(1)∵MP平分∠AMB,MQ平分∠AMC,
∴∠AMP=∠AMB,∠AMQ=∠AMC,
∴∠PMQ=∠AMP+∠AMQ=∠AMB+∠AMC
=(∠AMB+∠AMQ)
=×180°
=90°,
∴MP⊥MQ;
(2)∵BP⊥MP,CQ⊥MQ,
∴BP∥QM,∠BPM=90°,∠CQM=90°,
∴∠PBM=∠QMC,
∵AM是△ABC的中线,
∴BM=MC,
在△BMP和△MCQ中
,
∴△BMP≌△MCQ(AAS).
26.(1)∵,
∴,
∵,,
∴,
在和中,
,
∴,
∴.
(2)如图,作交的延长线于点F,
∵,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∵,
∴,
在和中,
,
∴,
∵.
(3)当点D在的延长线上时,作交的延长线于点G,则,
∵,
∵,,
∴,
在和中,
,
∴,
∴,
∵,
∴
∴,
∴,
∵,
∴,
在和中,
,
∴,
∴,
设,则,
∵,
∴,
∴,
∴,
,
∴,
∴的值为;
当点D在线段上时,作于点G,
同理可证:,,
设,则,
∵,
∴,
∴,
∴,
,
∴,
综上所述,的值为或,
故答案为:或.
一、单选题
1.关于全等三角形,下列说法正确的是( )
A.大小相等的三角形是全等三角形
B.面积相等的三角形是全等三角形
C.三个角对应相等的三角形是全等三角形
D.两个三角形全等,它们的形状一定相同
2.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
3.如图,用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是( )
A. B. C. D.
4.小刚把一块三角形玻璃打碎成了如图所示的三块,现要到玻璃店取配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去 B.带②去 C.带③去 D.带①和②去
5.如图,已知∠B=∠C,补充下列条件后,不能判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.∠AEB=∠ADC D.AB=AC
6.如图,△ABC≌△AEF,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
7.根据下列已知条件,能画出唯一的△ABC的是( )
A.AB=5,BC=4,AC=10 B.∠A=45°,∠C=60°,BC=8
C.∠A=80°,AB=6,BC=7 D.∠C=90°,AB=9
8.如图,在中,D,E是边上的两点,,则的度数为( )
A.90° B.80° C.70° D.60°
9.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
10.如图,已知点D、E分别在AB、AC上,BE与CD相交于点F,AB=AC,∠C=∠B,有3个结论:(1)∠AEB=∠ADC;(2)∠A+∠EFD=180°;(3)CE=BD,其中一定正确的( )
A.0个 B.1个 C.2个 D.3个
二、填空题
11.如图,在△ABC与△ACD中,AB∥CD,请添加一个条件:______,使△ABC≌△CDA.
12.如图,有两根钢条、,在中点处以小转轴连在一起做成工具(卡错),可测量工件内槽的宽.如果测量,那么工件内槽的宽______cm.
13.如图,在△ABC和△BAD中,因为AB=BA,∠ABC=∠BAD,_____=_____,根据“SAS”可以得到△ABC≌△BAD.
14.如图,已知△ABC≌△ABD,其中AC、BC的对应边分别是AD、BD,∠C=60°,∠ABC=80°,那么∠CAD=___度.
15.如图,点B、E、C、F在同一条直线上,AB∥DE,AB=DE,∠A=∠D,BF=10,BC=6,则EC=_____.
16.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x + y =________.
17.如图,已知△ADC的面积为5,AD平分∠BAC,且AD⊥BD于点D,那么△ABC的面积为_________.
18.如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若,则∠3=______°.
三、解答题
19.如图所示,与交于点E,,,.求证:.
20.如图,已知,,,求证:.
21.如图,在中,点是边的中点,过点作直线使,交的延长线于点.试说明的理由.
解:因为(已知),
所以 ( )
因为点是边的中点,
所以
在和中,
所以( )
所以( )
22.如图,已知E、F是BD上的两点,BE=DF,AE=CF,AE∥CF,请填写AD∥BC的理由.
解:因为AE∥CF(已知),
所以∠AED= (两直线平行,内错角相等).
因为BE=DF(已知),
所以BE+EF=DF+EF( ),
即BF=DE.
在△ADE与△CBF中
,
所以△ADE≌△CBF( ).
得∠ADE=∠CBF( ).
所以AD∥BC( ).
23.已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.
(1)请说明△AOC≌△BOD的理由;
(2)请说明OM=ON的理由.
24. 如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长
25.如图,已知在△ABC中,AM是△ABC的中线,MP平分∠AMBA,MQ平分∠AMC,且BP⊥MP于点P,CQ⊥MQ于点Q.
(1)求证:MP⊥MQ;
(2)求证:△BMP≌△MCQ.
26.已知:中,,,D为直线BC上一动点,连接AD,在直线AC右侧作,且.
(1)如图1,当点D在线段BC上时,过点E作于H,连接DE,求证:;
(2)如图2,当点D在线段BC的延长线上时,连接BE交CA的延长线于点M.
求证:;
(3)当点D在射线CB上时,连接BE交直线AC于M,若,则的值为______.
答案
一、单选题
1.D
【分析】根据全等三角形的定义:能够完全重合的两个三角形,对各个选项进行判断即可.
【解析】解:A、大小相等的三角形,形状不一定相同,所以不一定完全重合,故该选项不符合题意;
B、面积相等的三角形,形状不一定相同,所以不一定完全重合,故该选项不符合题意;
C、三个角对应相等的三角形,边长不一定相等,所以不一定完全重合,故该选项不符合题意;
D、两个三角形全等,它们的形状一定相同,故该选项符合题意;
故选:D.
2.A
【分析】根据∠α是b、c边的夹角,然后写出即可.
【解析】解:∵两个三角形全等,
∴∠α的度数是72°.
故选:A.
3.A
【分析】利用全等三角形的判定方法判断即可.
【解析】解:由作法易得,,,
在和中,
,
,
∴,
故选:A.
4.C
【分析】根据三角形全等的条件进行判断即可.
【解析】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据来配一块一样的玻璃,应带③去.
故选:C.
5.C
【分析】根据全等三角形的判定定理逐个判断即可.A可利用AAS判定;B可利用AAS判定;C只有三个对应角相等,无法证明;D可利用ASA判定.
【解析】A.∵∠B=∠C,∠A=∠A,AE=AD,
∴△ABE≌△ACD(AAS),故该选项不符合题意;
B.∵∠A=∠A,∠B=∠C,BE=CD,
∴△ABE≌△ACD(AAS),故该选项不符合题意;
C.由题意可知只有∠A=∠A,∠B=∠C,∠AEB=∠ADC三个已知条件,
∴无法由三个角对应相等证明三角形全等,故该选项符合题意;
D.∵∠B=∠C,AB=AC,∠A=∠A,
∴△ABE≌△ACD(ASA),故该选项不符合题意;
故选C.
6.C
【分析】根据全等三角形的性质即可进行判断.
【解析】∵△ABC≌△AEF,
∴AC=AF,EF=BC,
故①③正确;
∵△ABC≌△AEF,
∴∠EAF=∠BAC,
∴∠EAF-∠BAF=∠BAC-∠BAF,
∴∠EAB=∠FAC,
故④正确;
∠FAB=∠EAB不一定相等,故②不符合题意;
综上:正确的有3个,
故选:C.
7.B
【分析】要满足唯一画出△ABC,就要求选项给出的条件符合三角形全等的判定方法,不符合判定方法的画出的图形不一样,也就是三角形不唯一,而各选项中只有C选项符合ASA,是满足题目要求的,于是答案可得.
【解析】解:A、因为AB+BC<AC,所以这三边不能构成三角形;
B、已知两角可得到第三个角的度数,已知一边,则可以根据ASA来画一个三角形;
C、因为∠A不是已知两边的夹角,无法确定其他角的度数与边的长度;
D、只有一个角和一个边无法根据此作出一个三角形.
故选:B.
8.B
【分析】先证明BD=CE,然后证明△ADB≌△AEC,∠ADE=∠AED=70°,得到∠BAD=∠CAE,根据三角形内角和定理求出∠DAE=40°,从而求出∠BAD的度数即可得到答案.
【解析】解:∵BE=CD,
∴BE-DE=CD-DE,即BD=CE,
∵∠1=∠2=110°,AD=AE,
∴△ADB≌△AEC(SAS),∠ADE=∠AED=70°,
∴∠BAD=∠CAE,∠DAE=180°-∠ADE-∠AED=40°,
∵∠BAE=60°,
∴∠BAD=∠CAE=20°,
∴∠BAC=80°,
故选B.
9.C
【解析】要使△ABP与△ABC全等,
必须使点P到AB的距离等于点C到AB的距离,
即3个单位长度,
所以点P的位置可以是P1,P,P4三个,
故选C.
10.C
【分析】(1)通过证得△AEB≌△ADC,即可证得结论;
(2)根据题意,只有在CD⊥AB,BE⊥AC时,∠A+∠EFD=180°才成立;
(3)根据全等三角形的性质即可证得AD=AE,进而即可证得结论.
【解析】解:(1)在△AEB和△ADC中,
,
∴△AEB≌△ADC(ASA),
∴∠AEB=∠ADC,
故(1)正确;
(2)∵∠EFD=∠CEF+∠C,
∴∠A+∠EFD=∠CEF+∠A+∠C=∠CEF+∠BDF,
∵∠AEB=∠ADC,
∴∠CEF=∠BDF,
若∠A+∠EFD=180°,则∠CEF=∠BDF=90°,
故只有在CD⊥AB,BE⊥AC时,∠A+∠EFD=180°才成立,
故(2)错误;
(3)∵△AEB≌△ADC,
∴AD=AE,
∵AB=AC,
∴CE=BD,
故(3)正确;
综上,3个结论中一定正确的是(1)(3)两个,
故选:C.
二、填空题
11.AB=CD(答案不唯一)
【分析】根据平行线的性质可得∠BAC=∠DCA,再添加AB=CD可利用SAS判定△ABC≌△CDA.
【解析】解:添加AB=CD,理由如下:
∵AB∥CD,
∴∠BAC=∠DCA,
在△ABC和△CDA中,,
∴△ABC≌△CDA(SAS),
故答案为:AB=CD(答案不唯一).
12.2
【分析】利用SAS证明,即可得到答案.
【解析】解:由题意得:在△BOD和△AOC中,
,
∴,
∴,
故答案为:2.
13. BC AD
【分析】因为夹∠ABC的两边分别为AB的BC,所以再加上BC=AD,得△ABC≌△BAD(SAS).
【解析】解:∵AB=BA,∠ABC=∠BAD,
∴再加上BC=AD,
∴△ABC≌△BAD(SAS).
故答案为:①BC;②AD.
14.80
【分析】根据三角形的内角和定理得到∠CAB=180°-∠C-∠ABC=40°,根据全等三角形的性质得到∠DAB=∠CAB=40°,于是得到结论.
【解析】解:∵∠C=60°,∠ABC=80°,
∴∠CAB=180°-∠C-∠ABC=180°-60°-80°=40°,
∵△ABC≌△ABD,
∴∠DAB=∠CAB=40°,
∴∠CAD=∠CAB+∠DAB=80°,
故答案为:80.
15.2
【分析】根据平行线的性质得出∠B=∠DEF,即可利用ASA证明△ABC≌△DEF,根据全等三角形的性质得出BC=EF=6,即可根据线段的和差得解.
【解析】解:∵AB∥DE,
∴∠B=∠DEF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴BC=EF,
∵BF=10,BC=6,
∴EF=6,CF=BF﹣BC=4,
∴EC=EF﹣CF=2,
故答案为:2.
16.11
【分析】根据全等三角形的性质求出x和y即可.
【解析】解:∵这两个三角形全等
∴x=6,y=5
∴x + y =11
故答案为11.
17.10
【分析】首先延长BD,交AC于点E,再根据“ASA”证明△ABD≌△AED,由S△ADE+S△CDE=S△ABD+S△BCD,可知S△ABC=2 S△ACD,可得答案.
【解析】延长BD,交AC于点E,
∵AD平分∠BAE,
∴∠BAD=∠EAD.
∵∠ADB=∠ADE,AD=AD,
∴△ABD≌△AED,
∴BD=DE,
∴S△BCD= S△CDE,
∴S△ADE+S△CDE=S△ABD+S△BCD=5,
∴S△ABC=2 S△ACD=10.
故答案为:10
18.47
【分析】根据“边边边”证明,再根据全等三角形的性质可得∠ABC=∠1,∠BAC=∠2,然后利用三角形的一个外角等于与它不相邻的两个内角和求出∠3=∠1+∠2,然后求解即可.
【解析】解:在△ABC和△ADE中,,
∴(SSS),
∴∠ABC=∠1,∠BAC=∠2,
∴∠3=∠ABC+∠BAC=∠1+∠2,
∵,
∴,
∴.
故答案为:47.
三、解答题
19.,,
,
即BC=AD,
在和中,
(SSS)
20.∵
∴,即
∵
∴
又∵
∴ △DEF≌△ABC(SAS)
∴.
21.解:因为(已知),
所以∠E(两直线平行,内错角相等)
因为点是边的中点,
所以BD=CD.
在和中,
(对顶角相等)
所以(AAS)
所以(全等三角形的对应边相等)
22.证明:因为AE∥CF(已知),
所以∠AED=∠CFB(两直线平行,内错角相等),
因为BE=DF(已知),
所以BE+EF=DF+EF(等式的性质),
即BF=DE.
在△ADE与△CBF中,
,
所以△ADE≌△CBF(SAS),
得∠ADE=∠CBF(全等三角形的对应角相等),
所以AD∥BC(内错角相等,两直线平行),
故答案为:∠CFB;等式的性质;AE=CF,DE=BF;SAS;全等三角形的对应角相等;内错角相等,两直线平行.
23.(1)∵∠AOB=∠BOC=∠COD,
∴∠AOC=∠BOD,
在△AOC与△BOD中,
,
∴△AOC≌△BOD;
(2)∵△AOC≌△BOD,
∴∠A=∠B,
在△AOM与△BON中,
,
∴△AOM≌△BON,
∴OM=ON.
24.(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
在△DBC和△ECA中,
∵,
∴△DBC≌△ECA(AAS).
∴AE=CD;
(2)解:∵△CDB≌△AEC,
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC=BC=AC,且AC=12cm.
∴BD=6cm.
25.(1)∵MP平分∠AMB,MQ平分∠AMC,
∴∠AMP=∠AMB,∠AMQ=∠AMC,
∴∠PMQ=∠AMP+∠AMQ=∠AMB+∠AMC
=(∠AMB+∠AMQ)
=×180°
=90°,
∴MP⊥MQ;
(2)∵BP⊥MP,CQ⊥MQ,
∴BP∥QM,∠BPM=90°,∠CQM=90°,
∴∠PBM=∠QMC,
∵AM是△ABC的中线,
∴BM=MC,
在△BMP和△MCQ中
,
∴△BMP≌△MCQ(AAS).
26.(1)∵,
∴,
∵,,
∴,
在和中,
,
∴,
∴.
(2)如图,作交的延长线于点F,
∵,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∵,
∴,
在和中,
,
∴,
∵.
(3)当点D在的延长线上时,作交的延长线于点G,则,
∵,
∵,,
∴,
在和中,
,
∴,
∴,
∵,
∴
∴,
∴,
∵,
∴,
在和中,
,
∴,
∴,
设,则,
∵,
∴,
∴,
∴,
,
∴,
∴的值为;
当点D在线段上时,作于点G,
同理可证:,,
设,则,
∵,
∴,
∴,
∴,
,
∴,
综上所述,的值为或,
故答案为:或.
