七年级数学沪教版下册 14.2 全等三角形 试题(含解析)
文档属性
| 名称 | 七年级数学沪教版下册 14.2 全等三角形 试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 18:32:47 | ||
图片预览



文档简介
第2节 全等三角形
一、单选题
1.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形 B.两个等边三角形是全等图形
C.两个全等图形的面积一定相等 D.若两个图形周长相等,则它们一定是全等图形
2.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( ).
A.带其中的任意两块去都可以 B.带1、2或2、3去就可以了
C.带1、4或3、4去就可以了 D.带1、4或2、4或3、4去均可
3.如图,已知∠1=∠2,要使△ABC≌△ADE,还需条件( )
A.AB=AD,BC=DE B.BC=DE,AC=AE
C.∠B=∠D,∠C=∠E D.AC=AE,AB=AD
4.在和中,①,,;②,,;③,,;④,,;⑤,,能判断这两个三角形全等的条件有( )
A.①②④ B.①③⑤ C.④⑤ D.①③
5.如图,在中,,,是边上的中线,则的取值范围是( )
A. B. C. D.
6.如图,,点B和点C是对应顶点,,记,当时,与之间的数量关系为( )
A. B. C. D.
7.在和中,,,,,则这两个三角形的关系是( )
A.不一定全等 B.不全等 C.根据“ASA”全等 D.根据“SAS”全等
8.如图所示,设甲、乙、丙、丁分别表示△ABC,△ACD,△EFG,△EGH.已知∠ACB=∠CAD=∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则叙述正确的是( )
A.甲、乙全等,丙、丁全等 B.甲、乙全等,丙、丁不全等
C.甲、乙不全等,丙、丁全等 D.甲、乙不全等,丙、丁不全等
9.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位量为CD,当一端C下滑至时,另一端D向右滑到,则下列说法正确的是( )
A.下滑过程中,始终有
B.下滑过程中,始终有
C.若,则下滑过程中,一定存在某个位置使得
D.若,则下滑过程中,一定存在某个位置使得
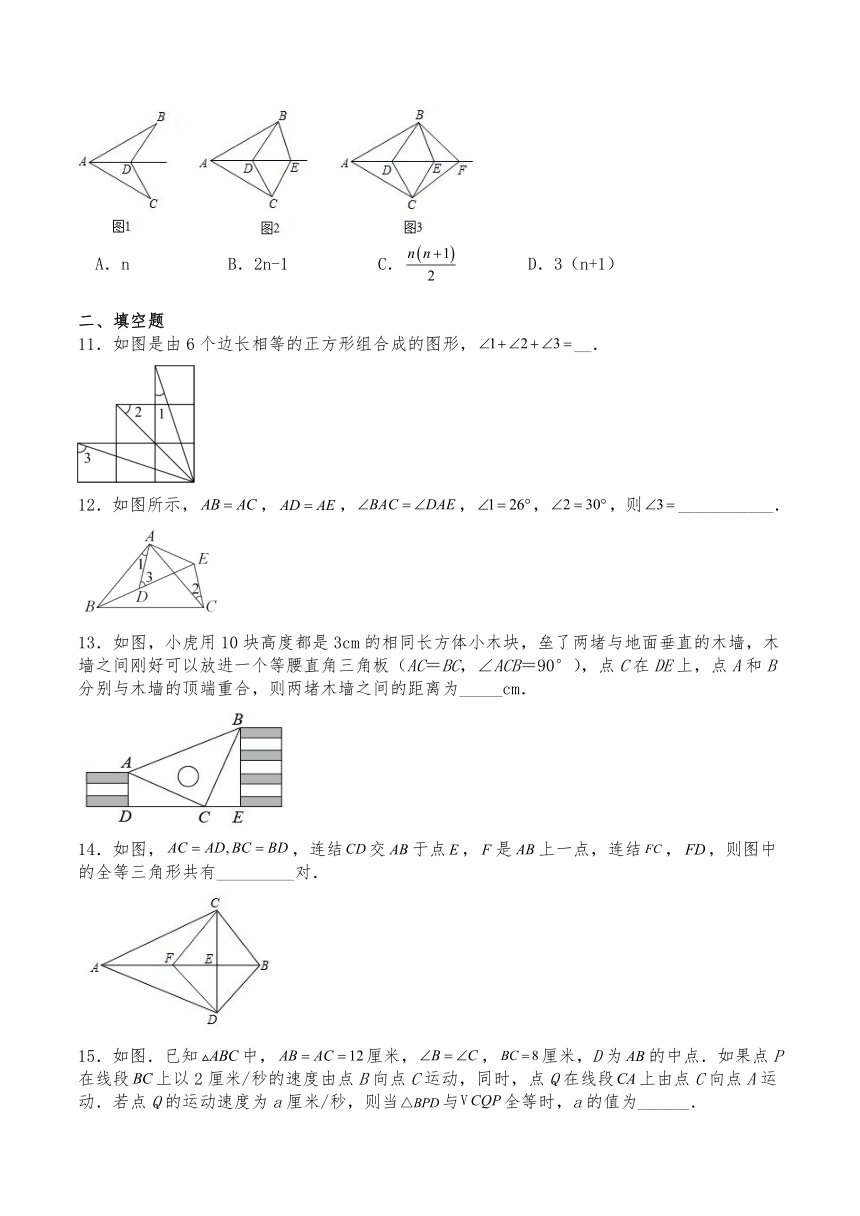
10.如图1,已知 AB=AC,D为∠BAC 的平分线上一点,连接 BD、 CD;如图2,已知 AB= AC,D、E为∠BAC的平分线上两点,连接 BD、CD、BE、CE;如图3,已知 AB=AC,D、E、F为∠BAC的平分线上三点,连接BD、CD、BE、CE、 BF、CF;…,依次规律,第 n个图形中全等三角形的对数是( )
A.n B.2n-1 C. D.3(n+1)
二、填空题
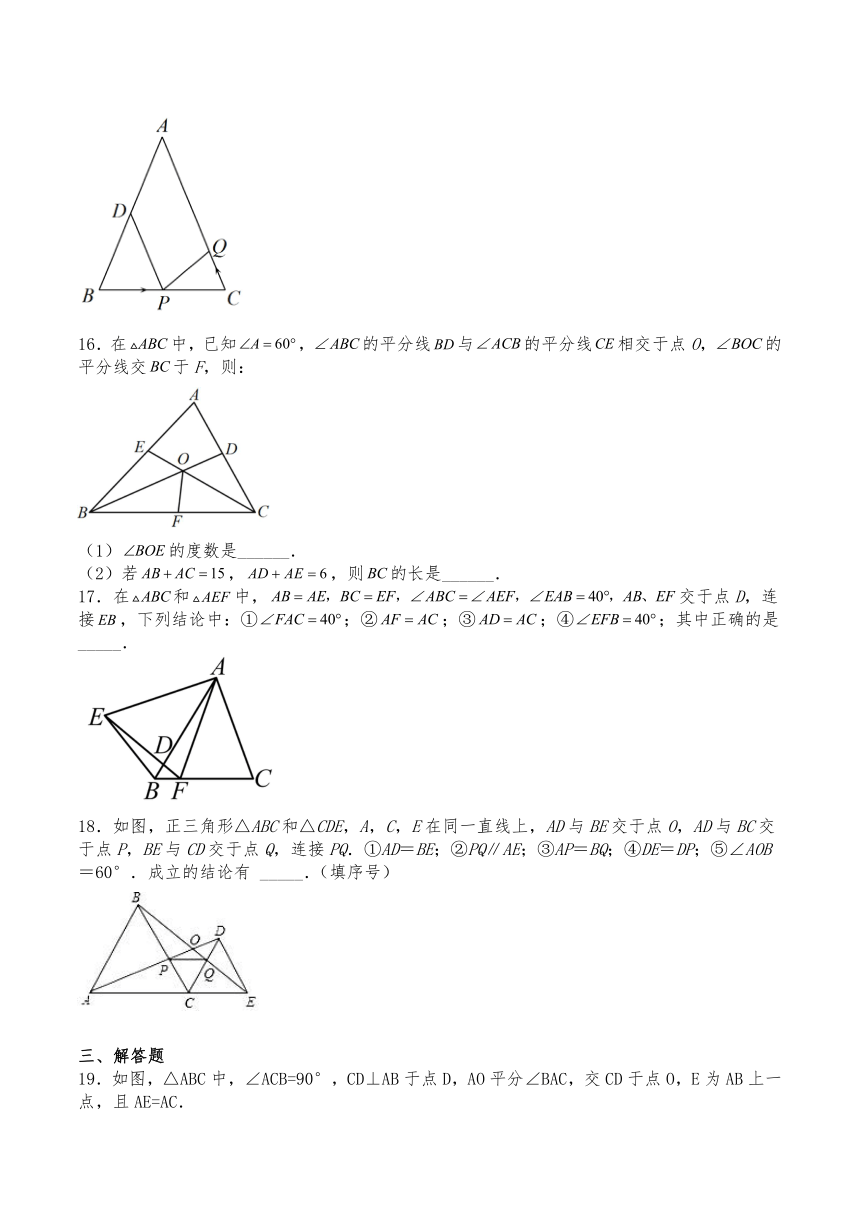
11.如图是由6个边长相等的正方形组合成的图形,__.
12.如图所示,,,,,,则___________.
13.如图,小虎用10块高度都是3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为_____cm.
14.如图,,连结交于点,是上一点,连结,,则图中的全等三角形共有_________对.
15.如图.已知中,厘米,,厘米,D为的中点.如果点P在线段上以2厘米/秒的速度由点B向点C运动,同时,点Q在线段上由点C向点A运动.若点Q的运动速度为a厘米/秒,则当与全等时,a的值为______.
16.在中,已知,的平分线与的平分线相交于点O,的平分线交于F,则:
(1)的度数是______.
(2)若,,则的长是______.
17.在和中,交于点D,连接,下列结论中:①;②;③;④;其中正确的是_____.
18.如图,正三角形△ABC和△CDE,A,C,E在同一直线上,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.成立的结论有 _____.(填序号)
三、解答题
19.如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC.
(1)求证:△AOC≌△AOE;
(2)求证:OE∥BC.
20.如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
解:EF、BC的位置关系是 .
说理如下:
因为AD是∠BAC的角平分线(已知)
所以∠1=∠2
在△AED和△ACD中,
所以△AED≌△ACD(SAS).
得 (全等三角形的对应边相等).
(完成以下说理过程)
21.如图,在中,,,是边上的中线,过点作于点,过点作交的延长线于点,连接.
(1)求证:;
(2)若,求的面积.
22.如图,已知,,,当不动,绕点旋转时,连接,交于点,试判断与的位置关系与数量关系,并证明你的结论.
23.如图,分别是的边上的高,且,.
求证:
(1);
(2).
24.如图,在中,,点在边上,,且,连,.
(1)求证:;
(2)求的度数.
25.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕点C旋转到图1所示位置时,求证:DE=AD-BE;
(2)当直线MN绕点C旋转到图2、图3所示位置时,补全图形,并探索线段DE、AD、BE之间的数量关系(直接写出答案).
26.已知:等边△ABC边长为3,点D、点E分别在射线AB、射线BC上,且BD=CE=a(0<a<3),将直线DE绕点E顺时针旋转60°,得到直线EF交直线AC于点F.
(1)如图1,当点D在线段AB上,点E在线段BC上时,说明BD+CF=3的理由.
(2)如图2,当点D在线段AB上,点E在线段BC的延长线上时,请判断线段BD,CF之间的数量关系并说明理由.
(3)当点D在线段AB延长线上时,线段BD,CF之间的数量关系又如何?请在备用图中画图探究,并直接写出线段BD,CF之间的数量关系.
27.问题提出,如图(1),在和中,,,,点E在内部,直线与交于点F,线段之间存在怎样的数量关系?
问题探究
(1)先将问题特殊化.如图(2),当点D,F重合时,直接写出一个等式,表示之间的数量关系;
(2)再探究一般情形.如图(1),当点D,F不重合时,证明(1)中的结论仍然成立.
问题拓展
(3)如图(3),在和中,,,,点E在内部,直线与交于点F,直线与交于点G,点H为线段上一点,,与交于点I,若,,则___________(用含m,n的式子表示)
答案
一、单选题
1.C
【分析】根据全等图形的判定和性质,对每个选项进行判断,即可得到答案.
【解析】解:A、两个面积相等的图形不一定是全等图形,故A错误;
B、两个等边三角形不一定是全等图形,故B错误;
C、两个全等图形的面积一定相等,正确;
D、若两个图形的周长相等,则它们不一定是全等形,故D错误;
故选:C.
2.D
【分析】②④虽没有原三角形完整的边,又没有角,但延长可得出原三角形的形状;带①、④可以用“角边角”确定三角形;带③、④也可以用“角边角”确定三角形.
【解析】解:带③、④可以用“角边角”确定三角形,
带①、④可以用“角边角”确定三角形,
带②④可以延长还原出原三角形,
故选D.
3.D
【分析】根据全等三角形的判定方法进行分析即可.根据:SSS、SAS、ASA、AAS、HL.
【解析】只有选项D. AC=AE,AB=AD,根据SAS,能使△ABC≌△ADE.其他是AAA、SSA,不能判定两个三角形全等.
故选D
4.B
【分析】依据全等三角形的判定定理进行判断即可.
【解析】解:第①组满足AAS,能证明△ABC≌△EFD.
第②组不是两角及一边对应相等,不能证明△ABC和△DEF全等.
第③组满足ASA,能证明△ABC≌△FDE.
第④组只是SSA,不能证明△ABC≌△FED.
第⑤组满足AAS,能证明△ABC≌△DEF.
故选B.
5.C
【分析】延长AD至点E,使得DE=AD,可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,从而得到的取值范围.
【解析】如图,延长AD至点E,使得DE=AD,
∵是边上的中线,
∴,
在△ABD和△CDE中,
,
∴△ABD△CDE(SAS),
∴AB=CE=5,AD=DE,
∵△ACE中,AC-CE<AE<AC+CE,
∴4<AE<14,
∴2<AD<7.
故选:C.
6.B
【分析】根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
【解析】∵,
∴,
∴,
在中,
∵,
∴,
∵,
∴,
∴,整理得,
故选:B.
7.D
【分析】由角度数量关系与三角形内角和定理可得,,由线段的数量关系可得,,进而可证明三角形全等.
【解析】解:∵,
∴,
∵
①+②得
②-①得
∴在和中,
∵
∴
故选D.
8.B
【分析】根据题意即是判断甲、乙是否全等,丙丁是否全等.运用判定定理解答.
【解析】解:∵∠ACB=CAD=70°,∠BAC=∠ACD=50°,AC为公共边,
∴△ABC≌△ACD,即甲、乙全等;
△EHG中,∠EGH=70°≠∠EHG=50°,即EH≠EG,
虽∠EFG=∠EGH=70°,∠EGF=∠EHG=50°,
∴△EFG不全等于△EGH,即丙、丁不全等.
综上所述甲、乙全等,丙、丁不全等,B正确,
故选:B.
9.D
【分析】根据全等三角形的性质解答即可.
【解析】将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至时,另端D向右滑到,当△OCD与全等时,,
A、下过程中,与不一定相等,说法错误;
B、下滑过程中,当△OCD与△ODC全等时,,说法错误;
C、若OC<OD,则下过程中,不存在某个位置使得,说法错误;
D、若OC>OD,则下过程中,当△OCD与△ODC全等时,一定存在某个位置使得,说法正确;
故选:D.
10.C
【分析】根据条件可得图1中△ABD≌△ACD有1对三角形全等;图2中可证出△ABD≌△ACD,△BDE≌△CDE,△ABE≌△ACE有3对三角形全等;图3中有6对三角形全等,根据数据可分析出第n个图形中全等三角形的对数.
【解析】解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD.
∴图1中有1对三角形全等;
同理图2中,△ABE≌△ACE,
∴BE=EC,
∵△ABD≌△ACD.
∴BD=CD,
又DE=DE,
∴△BDE≌△CDE,
∴图2中有3对三角形全等;
同理:图3中有6对三角形全等;
由此发现:第n个图形中全等三角形的对数是.
故选:C.
二、填空题
11.
【分析】根据已知先证明,得到,再根据求出结果.
【解析】解:如图,
根据题意得,,,,
为等腰直角三角形,
,
在和中,
,
∴,
,
,
,
.
故答案为.
12.
【分析】根据,得出,即可证明,根据三角形全等的性质得,最后利用可求解.
【解析】解:,
,
,
在和中,
,
,
,
,
故答案为:.
13.30
【分析】根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可,利用全等三角形的性质进行解答.
【解析】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=9cm,DC=BE=21cm,
∴DE=DC+CE=30(cm),
答:两堵木墙之间的距离为30cm.
故答案为:30.
14.6
【分析】根据全等三角形的判定定理逐个判断即可.
【解析】解:解:在△ACB和ADB中,
,
∴△ACB≌ADB,
∴∠CAB=∠DAB,∠CBA=∠DBA,
∵AC=AD,∠CAB=∠DAB,AF=AF
∴△CAF≌△DAF,CF=DF,
∵AC=AD,∠CAB=∠DAB,AE=AE
∴△ACE≌△ADE,CE=DE,
∵BC=BD,∠CBA=∠DBA,BE=BE
∴△CBE≌△DBE,
∵BC=BD,∠CBA=∠DBA,BF=BF
∴△FCB≌△FDB,
∵CF=DF,CE=DE,EF=EF,
∴△CEF≌△DEF,
∴图中全等的三角形有6对,
图中全等三角形有△ACB≌△ADB,△ACF≌△ADF,△ACE≌△ADE,△BCE≌△BDE,△BCF≌△BDF,△FCE≌△FDE,共6对,
故答案为:6 .
15.2或3
【分析】此题要分两种情况:①当BD=PC时,△BPD与△CQP全等,计算出BP的长,进而可得运动时间,然后再求a;②当BD=CQ时,△BDP≌△CQP,计算出BP的长,进而可得运动时间,然后再求a.
【解析】解:当BD=PC时,△BPD与△CQP全等,
∵点D为AB的中点,
∴BD=AB=6cm,
∵BD=PC,
∴BP=8-6=2(cm),
∵点P在线段BC上以2厘米/秒的速度由B点向C点运动,
∴运动时间时1s,
∵△DBP≌△PCQ,
∴BP=CQ=2cm,
∴a=2÷1=2;
当BD=CQ时,△BDP≌△CQP,
∵BD=6cm,PB=PC,
∴QC=6cm,
∵BC=8cm,
∴BP=4cm,
∴运动时间为4÷2=2(s),
∴a=6÷2=3(m/s),
故答案为:2或3.
16. 9
【分析】(1)利用三角形内角和定理和角平分线的定义求出的度数即可利用平角的定义求出的度数;
(2)利用证明,得到,同理,利用线段和差关系得到即可得到答案.
【解析】解:(1)∵在中,,
∴,
∵的平分线与的平分线相交于点O,
∴,
∴,
∴,
故答案为:;
(2)∵平分,
∴,
又∵,
∴,
∴,
同理,
∵,,
∴,即,
∴,
故答案为:9.
17.①②④
【分析】由“”可证,由全等三角形的性质依次判断可求解.
【解析】解:在和中,
,
∴,
∴故②正确,
∴,故①正确,
∵,
∴,故④正确,
无法证明,故③错误,
故答案为:①②④.
18.①②③⑤
【分析】①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE;
③由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ(ASA),所以AP=BQ;故③正确;
②根据③△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;
④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;
⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.
【解析】解:①∵等边△ABC和等边△DCE,
∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
故①正确;
③∵△ACD≌△BCE(已证),
∴∠CAD=∠CBE,
∵∠ACB=∠ECD=60°(已证),
∴∠BCQ=180°﹣60°×2=60°,
∴∠ACB=∠BCQ=60°,
在△ACP与△BCQ中,
,
∴△ACP≌△BCQ(ASA),
∴AP=BQ;
故③正确;
②∵△ACP≌△BCQ,
∴PC=QC,
∴△PCQ是等边三角形,
∴∠CPQ=60°,
∴∠ACB=∠CPQ,
∴PQ∥AE;
故②正确;
④∵AD=BE,AP=BQ,
∴AD﹣AP=BE﹣BQ,
即DP=QE,
∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,
∴DE≠QE,
∴DP≠DE;
故④错误;
⑤∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵等边△DCE,
∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.
故⑤正确;
综上所述,正确的结论有:①②③⑤.
故答案为:①②③⑤.
三、解答题
19.
(1)∵AO平分∠BAC,
∴∠CAO=∠EAO.
在△ACO和△AEO中:
,
∴△AOC≌△AOE.
(2)∵△AOC≌△AOE,
∴∠ACO=∠AEO,
∵ CD⊥AB于点D,
∴∠ODE=∠ACB=90°,
∴∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,
∴∠DCB=∠DOE,
∴OE∥BC.
20.解:EF、BC的位置关系是EF∥BC.
理由如下:
如图,
∵AD是∠BAC的角平分线(已知)
∴∠1=∠2.
在△AED和△ACD中,
∴△AED≌△ACD(SAS).
∴DE=DC (全等三角形的对应边相等),
∴∠3=∠4.
∵EC平分∠DEF(已知),
∴∠3=∠5.
∴∠4=∠5.
所以EF∥BC(内错角相等,两直线平行).
故答案为:EF∥BC;;DE=DC;
21.(1)证明:∵在中,,,
∴,
∴,
又∵,
∴,
在和中,
∵,
∴;
(2)解:∵是边上的中线,
∴,
由(1)知,
∴,
∴.
22.解:,,证明如下:
∠ACB=∠DCE=900,
,即,
在和中,,
,
,,
又,
,
,即,
,
.
23.(1)证明:由题意得,
∴,,
∴,
在△ADC和△CEB中,
∵,
∴△ABP≌△QCA(SAS) ,
∴.
(2)证明:∵△ABP≌△QCA(SAS),
∴,
∵,
∴,
∴,
∴.
24.(1)证明:∵,
∴,即,
在和中,
∴,
∴;
(2)解:∵,
∴,
∴.
25.
(1)
证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90,
在Rt△CEB中,∠CBE+∠BCE=90,
又∠ACB=90°,
∴∠ACD+∠BCE=90,
∴∠CBE=∠ACD,
在△ADC与△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CE-CD=AD-BE;
(2)
如图2所示:DE=BE-AD;如图3所示:DE=BE+AD,
理由:如图2,∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90,
在Rt△CEB中,∠CBE+∠BCE=90,
又∠ACB=90°,
∴∠ACD+∠BCE=90,
∴∠CBE=∠ACD,
在△ADC与△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CD-CE=BE-AD;
图3的证明方法与图2相同,均是通过证明△ADC≌△CEB(AAS)来得到结论.
26.解:(1)∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE且∠DEF﹣60°=∠B,
∴∠BDE=∠FEC,
又∵BD=CE,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD+CF=CE+BE=BC=3;
(2)如下图,设G点在FE的延长线,AF与DE交点为H,
∴∠DEG=∠F+∠FHE=60°,∠BCA=∠FHE+∠BED=60°,
∴∠F=∠BED,
又∵∠B=∠FCE=60°,CE=BD,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD=CE=BE﹣BC=CF﹣BC,
即BD=CF﹣3;
(3)①若E在线段BC上,设DE延长线交AC于点I,
∵∠ABC=∠BDE+∠BED=60°,∠IEF=∠IEC+∠CEF=60°,∠BED=∠IEC,
∴∠BDE=∠CEF,
又∵∠DBE=∠ECF=120°,CE=BD,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD+CF=CE+BE=BC=3;
②若E在BC延长线上,
∵∠ABC=∠BDE+∠BED=60°,∠FED=∠FEC+∠BED=60°,
∴∠BDE=∠FEC,
又∵∠DBE=∠FCE=120°,BD=CE,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴CF﹣BD=BE﹣CE=BC=3;
综上,若E在线段BC上,BD+CF=3;若E在BC延长线上,CF﹣BD=3.
27.(1)解:如图2,
在和中,
,,,
和是等边三角形,
,
即,
,
,
,
又,,
,
,
即,
,
即;
(2)成立,
如图,将绕点C旋转交于点M,
,
,
,
由(1)可知,
,
,
又,
,
,,
又,
是等边三角形,
,
,
即;
(3)如图,将绕点C旋转交的延长线于点N,连接,
,
,
,
,
,
由(1)可知,
,
,
又,
,,
又,
,
,
,
,
,
,
,
,
,
,,
,
故答案为:.
一、单选题
1.下列说法中正确的是( )
A.两个面积相等的图形,一定是全等图形 B.两个等边三角形是全等图形
C.两个全等图形的面积一定相等 D.若两个图形周长相等,则它们一定是全等图形
2.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( ).
A.带其中的任意两块去都可以 B.带1、2或2、3去就可以了
C.带1、4或3、4去就可以了 D.带1、4或2、4或3、4去均可
3.如图,已知∠1=∠2,要使△ABC≌△ADE,还需条件( )
A.AB=AD,BC=DE B.BC=DE,AC=AE
C.∠B=∠D,∠C=∠E D.AC=AE,AB=AD
4.在和中,①,,;②,,;③,,;④,,;⑤,,能判断这两个三角形全等的条件有( )
A.①②④ B.①③⑤ C.④⑤ D.①③
5.如图,在中,,,是边上的中线,则的取值范围是( )
A. B. C. D.
6.如图,,点B和点C是对应顶点,,记,当时,与之间的数量关系为( )
A. B. C. D.
7.在和中,,,,,则这两个三角形的关系是( )
A.不一定全等 B.不全等 C.根据“ASA”全等 D.根据“SAS”全等
8.如图所示,设甲、乙、丙、丁分别表示△ABC,△ACD,△EFG,△EGH.已知∠ACB=∠CAD=∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则叙述正确的是( )
A.甲、乙全等,丙、丁全等 B.甲、乙全等,丙、丁不全等
C.甲、乙不全等,丙、丁全等 D.甲、乙不全等,丙、丁不全等
9.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位量为CD,当一端C下滑至时,另一端D向右滑到,则下列说法正确的是( )
A.下滑过程中,始终有
B.下滑过程中,始终有
C.若,则下滑过程中,一定存在某个位置使得
D.若,则下滑过程中,一定存在某个位置使得
10.如图1,已知 AB=AC,D为∠BAC 的平分线上一点,连接 BD、 CD;如图2,已知 AB= AC,D、E为∠BAC的平分线上两点,连接 BD、CD、BE、CE;如图3,已知 AB=AC,D、E、F为∠BAC的平分线上三点,连接BD、CD、BE、CE、 BF、CF;…,依次规律,第 n个图形中全等三角形的对数是( )
A.n B.2n-1 C. D.3(n+1)
二、填空题
11.如图是由6个边长相等的正方形组合成的图形,__.
12.如图所示,,,,,,则___________.
13.如图,小虎用10块高度都是3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为_____cm.
14.如图,,连结交于点,是上一点,连结,,则图中的全等三角形共有_________对.
15.如图.已知中,厘米,,厘米,D为的中点.如果点P在线段上以2厘米/秒的速度由点B向点C运动,同时,点Q在线段上由点C向点A运动.若点Q的运动速度为a厘米/秒,则当与全等时,a的值为______.
16.在中,已知,的平分线与的平分线相交于点O,的平分线交于F,则:
(1)的度数是______.
(2)若,,则的长是______.
17.在和中,交于点D,连接,下列结论中:①;②;③;④;其中正确的是_____.
18.如图,正三角形△ABC和△CDE,A,C,E在同一直线上,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.成立的结论有 _____.(填序号)
三、解答题
19.如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC.
(1)求证:△AOC≌△AOE;
(2)求证:OE∥BC.
20.如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
解:EF、BC的位置关系是 .
说理如下:
因为AD是∠BAC的角平分线(已知)
所以∠1=∠2
在△AED和△ACD中,
所以△AED≌△ACD(SAS).
得 (全等三角形的对应边相等).
(完成以下说理过程)
21.如图,在中,,,是边上的中线,过点作于点,过点作交的延长线于点,连接.
(1)求证:;
(2)若,求的面积.
22.如图,已知,,,当不动,绕点旋转时,连接,交于点,试判断与的位置关系与数量关系,并证明你的结论.
23.如图,分别是的边上的高,且,.
求证:
(1);
(2).
24.如图,在中,,点在边上,,且,连,.
(1)求证:;
(2)求的度数.
25.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕点C旋转到图1所示位置时,求证:DE=AD-BE;
(2)当直线MN绕点C旋转到图2、图3所示位置时,补全图形,并探索线段DE、AD、BE之间的数量关系(直接写出答案).
26.已知:等边△ABC边长为3,点D、点E分别在射线AB、射线BC上,且BD=CE=a(0<a<3),将直线DE绕点E顺时针旋转60°,得到直线EF交直线AC于点F.
(1)如图1,当点D在线段AB上,点E在线段BC上时,说明BD+CF=3的理由.
(2)如图2,当点D在线段AB上,点E在线段BC的延长线上时,请判断线段BD,CF之间的数量关系并说明理由.
(3)当点D在线段AB延长线上时,线段BD,CF之间的数量关系又如何?请在备用图中画图探究,并直接写出线段BD,CF之间的数量关系.
27.问题提出,如图(1),在和中,,,,点E在内部,直线与交于点F,线段之间存在怎样的数量关系?
问题探究
(1)先将问题特殊化.如图(2),当点D,F重合时,直接写出一个等式,表示之间的数量关系;
(2)再探究一般情形.如图(1),当点D,F不重合时,证明(1)中的结论仍然成立.
问题拓展
(3)如图(3),在和中,,,,点E在内部,直线与交于点F,直线与交于点G,点H为线段上一点,,与交于点I,若,,则___________(用含m,n的式子表示)
答案
一、单选题
1.C
【分析】根据全等图形的判定和性质,对每个选项进行判断,即可得到答案.
【解析】解:A、两个面积相等的图形不一定是全等图形,故A错误;
B、两个等边三角形不一定是全等图形,故B错误;
C、两个全等图形的面积一定相等,正确;
D、若两个图形的周长相等,则它们不一定是全等形,故D错误;
故选:C.
2.D
【分析】②④虽没有原三角形完整的边,又没有角,但延长可得出原三角形的形状;带①、④可以用“角边角”确定三角形;带③、④也可以用“角边角”确定三角形.
【解析】解:带③、④可以用“角边角”确定三角形,
带①、④可以用“角边角”确定三角形,
带②④可以延长还原出原三角形,
故选D.
3.D
【分析】根据全等三角形的判定方法进行分析即可.根据:SSS、SAS、ASA、AAS、HL.
【解析】只有选项D. AC=AE,AB=AD,根据SAS,能使△ABC≌△ADE.其他是AAA、SSA,不能判定两个三角形全等.
故选D
4.B
【分析】依据全等三角形的判定定理进行判断即可.
【解析】解:第①组满足AAS,能证明△ABC≌△EFD.
第②组不是两角及一边对应相等,不能证明△ABC和△DEF全等.
第③组满足ASA,能证明△ABC≌△FDE.
第④组只是SSA,不能证明△ABC≌△FED.
第⑤组满足AAS,能证明△ABC≌△DEF.
故选B.
5.C
【分析】延长AD至点E,使得DE=AD,可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,从而得到的取值范围.
【解析】如图,延长AD至点E,使得DE=AD,
∵是边上的中线,
∴,
在△ABD和△CDE中,
,
∴△ABD△CDE(SAS),
∴AB=CE=5,AD=DE,
∵△ACE中,AC-CE<AE<AC+CE,
∴4<AE<14,
∴2<AD<7.
故选:C.
6.B
【分析】根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
【解析】∵,
∴,
∴,
在中,
∵,
∴,
∵,
∴,
∴,整理得,
故选:B.
7.D
【分析】由角度数量关系与三角形内角和定理可得,,由线段的数量关系可得,,进而可证明三角形全等.
【解析】解:∵,
∴,
∵
①+②得
②-①得
∴在和中,
∵
∴
故选D.
8.B
【分析】根据题意即是判断甲、乙是否全等,丙丁是否全等.运用判定定理解答.
【解析】解:∵∠ACB=CAD=70°,∠BAC=∠ACD=50°,AC为公共边,
∴△ABC≌△ACD,即甲、乙全等;
△EHG中,∠EGH=70°≠∠EHG=50°,即EH≠EG,
虽∠EFG=∠EGH=70°,∠EGF=∠EHG=50°,
∴△EFG不全等于△EGH,即丙、丁不全等.
综上所述甲、乙全等,丙、丁不全等,B正确,
故选:B.
9.D
【分析】根据全等三角形的性质解答即可.
【解析】将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至时,另端D向右滑到,当△OCD与全等时,,
A、下过程中,与不一定相等,说法错误;
B、下滑过程中,当△OCD与△ODC全等时,,说法错误;
C、若OC<OD,则下过程中,不存在某个位置使得,说法错误;
D、若OC>OD,则下过程中,当△OCD与△ODC全等时,一定存在某个位置使得,说法正确;
故选:D.
10.C
【分析】根据条件可得图1中△ABD≌△ACD有1对三角形全等;图2中可证出△ABD≌△ACD,△BDE≌△CDE,△ABE≌△ACE有3对三角形全等;图3中有6对三角形全等,根据数据可分析出第n个图形中全等三角形的对数.
【解析】解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD.
∴图1中有1对三角形全等;
同理图2中,△ABE≌△ACE,
∴BE=EC,
∵△ABD≌△ACD.
∴BD=CD,
又DE=DE,
∴△BDE≌△CDE,
∴图2中有3对三角形全等;
同理:图3中有6对三角形全等;
由此发现:第n个图形中全等三角形的对数是.
故选:C.
二、填空题
11.
【分析】根据已知先证明,得到,再根据求出结果.
【解析】解:如图,
根据题意得,,,,
为等腰直角三角形,
,
在和中,
,
∴,
,
,
,
.
故答案为.
12.
【分析】根据,得出,即可证明,根据三角形全等的性质得,最后利用可求解.
【解析】解:,
,
,
在和中,
,
,
,
,
故答案为:.
13.30
【分析】根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可,利用全等三角形的性质进行解答.
【解析】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=9cm,DC=BE=21cm,
∴DE=DC+CE=30(cm),
答:两堵木墙之间的距离为30cm.
故答案为:30.
14.6
【分析】根据全等三角形的判定定理逐个判断即可.
【解析】解:解:在△ACB和ADB中,
,
∴△ACB≌ADB,
∴∠CAB=∠DAB,∠CBA=∠DBA,
∵AC=AD,∠CAB=∠DAB,AF=AF
∴△CAF≌△DAF,CF=DF,
∵AC=AD,∠CAB=∠DAB,AE=AE
∴△ACE≌△ADE,CE=DE,
∵BC=BD,∠CBA=∠DBA,BE=BE
∴△CBE≌△DBE,
∵BC=BD,∠CBA=∠DBA,BF=BF
∴△FCB≌△FDB,
∵CF=DF,CE=DE,EF=EF,
∴△CEF≌△DEF,
∴图中全等的三角形有6对,
图中全等三角形有△ACB≌△ADB,△ACF≌△ADF,△ACE≌△ADE,△BCE≌△BDE,△BCF≌△BDF,△FCE≌△FDE,共6对,
故答案为:6 .
15.2或3
【分析】此题要分两种情况:①当BD=PC时,△BPD与△CQP全等,计算出BP的长,进而可得运动时间,然后再求a;②当BD=CQ时,△BDP≌△CQP,计算出BP的长,进而可得运动时间,然后再求a.
【解析】解:当BD=PC时,△BPD与△CQP全等,
∵点D为AB的中点,
∴BD=AB=6cm,
∵BD=PC,
∴BP=8-6=2(cm),
∵点P在线段BC上以2厘米/秒的速度由B点向C点运动,
∴运动时间时1s,
∵△DBP≌△PCQ,
∴BP=CQ=2cm,
∴a=2÷1=2;
当BD=CQ时,△BDP≌△CQP,
∵BD=6cm,PB=PC,
∴QC=6cm,
∵BC=8cm,
∴BP=4cm,
∴运动时间为4÷2=2(s),
∴a=6÷2=3(m/s),
故答案为:2或3.
16. 9
【分析】(1)利用三角形内角和定理和角平分线的定义求出的度数即可利用平角的定义求出的度数;
(2)利用证明,得到,同理,利用线段和差关系得到即可得到答案.
【解析】解:(1)∵在中,,
∴,
∵的平分线与的平分线相交于点O,
∴,
∴,
∴,
故答案为:;
(2)∵平分,
∴,
又∵,
∴,
∴,
同理,
∵,,
∴,即,
∴,
故答案为:9.
17.①②④
【分析】由“”可证,由全等三角形的性质依次判断可求解.
【解析】解:在和中,
,
∴,
∴故②正确,
∴,故①正确,
∵,
∴,故④正确,
无法证明,故③错误,
故答案为:①②④.
18.①②③⑤
【分析】①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE;
③由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ(ASA),所以AP=BQ;故③正确;
②根据③△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;
④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;
⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.
【解析】解:①∵等边△ABC和等边△DCE,
∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
故①正确;
③∵△ACD≌△BCE(已证),
∴∠CAD=∠CBE,
∵∠ACB=∠ECD=60°(已证),
∴∠BCQ=180°﹣60°×2=60°,
∴∠ACB=∠BCQ=60°,
在△ACP与△BCQ中,
,
∴△ACP≌△BCQ(ASA),
∴AP=BQ;
故③正确;
②∵△ACP≌△BCQ,
∴PC=QC,
∴△PCQ是等边三角形,
∴∠CPQ=60°,
∴∠ACB=∠CPQ,
∴PQ∥AE;
故②正确;
④∵AD=BE,AP=BQ,
∴AD﹣AP=BE﹣BQ,
即DP=QE,
∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,
∴DE≠QE,
∴DP≠DE;
故④错误;
⑤∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵等边△DCE,
∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.
故⑤正确;
综上所述,正确的结论有:①②③⑤.
故答案为:①②③⑤.
三、解答题
19.
(1)∵AO平分∠BAC,
∴∠CAO=∠EAO.
在△ACO和△AEO中:
,
∴△AOC≌△AOE.
(2)∵△AOC≌△AOE,
∴∠ACO=∠AEO,
∵ CD⊥AB于点D,
∴∠ODE=∠ACB=90°,
∴∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,
∴∠DCB=∠DOE,
∴OE∥BC.
20.解:EF、BC的位置关系是EF∥BC.
理由如下:
如图,
∵AD是∠BAC的角平分线(已知)
∴∠1=∠2.
在△AED和△ACD中,
∴△AED≌△ACD(SAS).
∴DE=DC (全等三角形的对应边相等),
∴∠3=∠4.
∵EC平分∠DEF(已知),
∴∠3=∠5.
∴∠4=∠5.
所以EF∥BC(内错角相等,两直线平行).
故答案为:EF∥BC;;DE=DC;
21.(1)证明:∵在中,,,
∴,
∴,
又∵,
∴,
在和中,
∵,
∴;
(2)解:∵是边上的中线,
∴,
由(1)知,
∴,
∴.
22.解:,,证明如下:
∠ACB=∠DCE=900,
,即,
在和中,,
,
,,
又,
,
,即,
,
.
23.(1)证明:由题意得,
∴,,
∴,
在△ADC和△CEB中,
∵,
∴△ABP≌△QCA(SAS) ,
∴.
(2)证明:∵△ABP≌△QCA(SAS),
∴,
∵,
∴,
∴,
∴.
24.(1)证明:∵,
∴,即,
在和中,
∴,
∴;
(2)解:∵,
∴,
∴.
25.
(1)
证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90,
在Rt△CEB中,∠CBE+∠BCE=90,
又∠ACB=90°,
∴∠ACD+∠BCE=90,
∴∠CBE=∠ACD,
在△ADC与△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CE-CD=AD-BE;
(2)
如图2所示:DE=BE-AD;如图3所示:DE=BE+AD,
理由:如图2,∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90,
在Rt△CEB中,∠CBE+∠BCE=90,
又∠ACB=90°,
∴∠ACD+∠BCE=90,
∴∠CBE=∠ACD,
在△ADC与△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CD-CE=BE-AD;
图3的证明方法与图2相同,均是通过证明△ADC≌△CEB(AAS)来得到结论.
26.解:(1)∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE且∠DEF﹣60°=∠B,
∴∠BDE=∠FEC,
又∵BD=CE,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD+CF=CE+BE=BC=3;
(2)如下图,设G点在FE的延长线,AF与DE交点为H,
∴∠DEG=∠F+∠FHE=60°,∠BCA=∠FHE+∠BED=60°,
∴∠F=∠BED,
又∵∠B=∠FCE=60°,CE=BD,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD=CE=BE﹣BC=CF﹣BC,
即BD=CF﹣3;
(3)①若E在线段BC上,设DE延长线交AC于点I,
∵∠ABC=∠BDE+∠BED=60°,∠IEF=∠IEC+∠CEF=60°,∠BED=∠IEC,
∴∠BDE=∠CEF,
又∵∠DBE=∠ECF=120°,CE=BD,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴BD+CF=CE+BE=BC=3;
②若E在BC延长线上,
∵∠ABC=∠BDE+∠BED=60°,∠FED=∠FEC+∠BED=60°,
∴∠BDE=∠FEC,
又∵∠DBE=∠FCE=120°,BD=CE,
∴△DBE≌△ECF(AAS),
∴CF=BE,
∴CF﹣BD=BE﹣CE=BC=3;
综上,若E在线段BC上,BD+CF=3;若E在BC延长线上,CF﹣BD=3.
27.(1)解:如图2,
在和中,
,,,
和是等边三角形,
,
即,
,
,
,
又,,
,
,
即,
,
即;
(2)成立,
如图,将绕点C旋转交于点M,
,
,
,
由(1)可知,
,
,
又,
,
,,
又,
是等边三角形,
,
,
即;
(3)如图,将绕点C旋转交的延长线于点N,连接,
,
,
,
,
,
由(1)可知,
,
,
又,
,,
又,
,
,
,
,
,
,
,
,
,
,,
,
故答案为:.
