七年级数学下册试题第13章《相交线 平行线》单元综合复习题-沪教版(含解析)
文档属性
| 名称 | 七年级数学下册试题第13章《相交线 平行线》单元综合复习题-沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
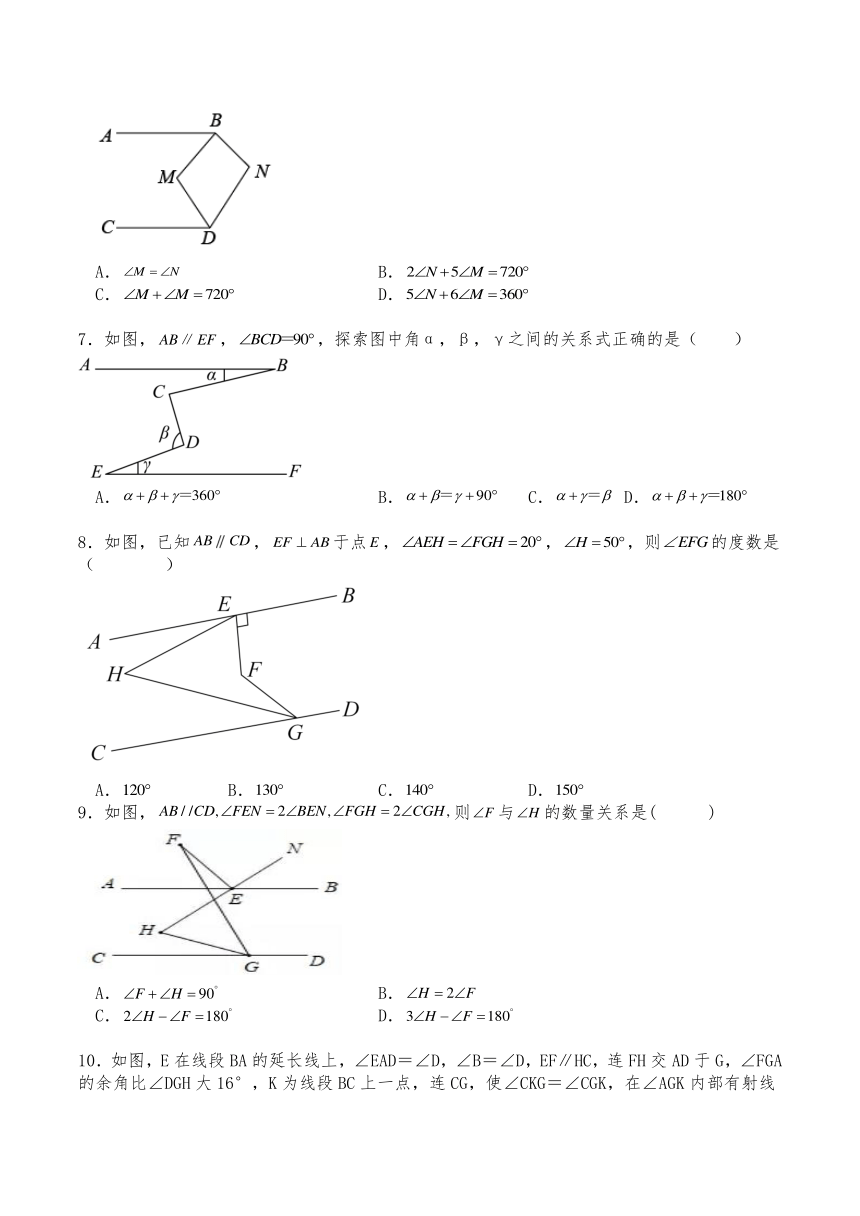
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 16:18:21 | ||
图片预览




文档简介
第13章《相交线 平行线》单元综合复习题
一、单选题
1.两条平行直线被第三条直线所截时,产生的八个角中,角平分线互相平行的两个角是( ).
A.同位角 B.同旁内角 C.内错角 D.同位角或内错角
2.一副直角三角板如图放置,点C在的延长线上,,,,,则为( )
A. B. C. D.
3.如图,已知直线,被直线所截,,E是平面内任意一点(点E不在直线,,上),设,.下列各式:①,②,③,④,的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
4.平面内三条直线的交点个数可能有〔 〕
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3
5.一辆汽车在笔直的公路上行驶,两次拐弯后,还在原来的方向上平行前进,那么这两次拐弯的角度应是( )
A.第一次右拐,第二次左拐 B.第一次左拐,第二次右拐
C.第一次左拐,第二次左拐 D.第一次右拐,第二次右拐
6.如图,已知AB∥CD,,.则与之间满足的数量关系是( )
A. B.
C. D.
7.如图,,,探索图中角α,β,γ之间的关系式正确的是( )
A. B. C. D.
8.如图,已知,于点,,,则的度数是( )
A. B. C. D.
9.如图,则与的数量关系是( )
A. B.
C. D.
10.如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EF∥HC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①AD∥BC;②GK平分∠AGC;③∠E+∠EAG+∠HCK=180°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.如图,已知∠1=72°,∠4=110°,∠3=70°,则∠2=____________.
12.如图,,与相交于点,且,,若,则______.
13.如图,,一副三角板(其中,,)按如图所示的位置摆放.若,则的度数为__________(用含的代数式表示).
14.如图,直线相交于点O.已知把分成两个角,且,将射线绕点O逆时针旋转到,若时,的度数是___________.
15.如图,已知,,,则________度.
16.某市拟定在中央公园建设大型灯光秀,在某平行湖道两岸所在直线、安装探照灯,若灯P发出的光束自逆时针旋转至便立即回转,灯Q发出的光束自逆时针旋转至便立即回转,每天晚间两灯同时开启不停交叉照射巡视.设灯P光束转动的速度是10度/秒,灯Q光束转动的速度是4度/秒,在两灯同时开启后的35秒内,开启______秒时,两灯的光束互相垂直.
17.如图,已知直线,点,分别在直线,上,点为,之间一点,且点在的右侧,.若与的平分线相交于点,与的平分线相交于点,与的平分线相交于点……以此类推,若,则的值是______.
三、解答题
18.如图所示的正方形网格,所有小正方形的边长都为1,、、都在格点上.
(1)利用网格作图:
①过点画直线的平行线;
②过点画直线的垂线,垂足为点;
(2)线段的长度是点________到直线________的距离;
(3)比较大小:________(填>、<或=),理由:________.
19.如图,已知,,,试判定 与 的位置关系,并说明理由.
解:.
理由:∵(已知)
∴
∵(已知)
∴______ (同位角相等,两直线平行)
∴______(______)
∵(已知)
∴______ (等量代换)
∴DEBF(______)
∴(______)
∴(垂直的定义)
(1)请补全上面说理过程;
(2)若,求出的度数,并说明理由;
(3)直接写出和的关系______.
20.(1)如图(1),当、、满足条件______时,有ABCD,并说明理由.
(2)如图(2),当ABCD时,,,的关系是______.
21.已知,点为平面内的一点,.
(1)当点在如图①的位置时,求与的数量关系.
解: .(根据如图填射线的画法)
因为,
所以 ( ).
所以(两直线平行,内错角相等);
(请继续完成接下去的说理过程)
(2)当点在如图②的位置时,与的数量关系是 (直接写出答案);
(3)在(2)的条件下,如图③,过点作,垂足为点,与的平分线分别交射线于点、,回答下列问题(直接写出答案):图中与相等的角是 , 度.
22.如图,AB//CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P,且满足0°<∠EPF<180°,QE,QF分别平分∠PEB和∠PFD.在探究∠EPF与∠EQF之间的数量关系时,我们需要对点P的位置进行分类讨论:
(1)如图1,当P点在EF的右侧时,若∠EPF=110°,则∠EQF= ;猜想∠EPF与∠EQF的数量关系,请直接写出结果;
(2)如图2,当P点在EF的左侧时,探究∠EPF与∠EQF的数量关系,请说明理由;
(3)若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3;…以此类推,则∠EPF与∠EQ2021F满足怎样的数量关系?
23.已知:如图(1)直线AB、CD被直线MN所截,∠1=∠2.
(1)求证:AB∥CD;
(2)如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;
(3)如图(3),在(2)的条件下,过P点作PH∥EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.
24.“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯,如图1所示,灯A射线从开始顺时针旋转至便立即回转,灯B射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度,假定主道路是平行的,即,且.
(1)填空:_________;
(2)①若灯B射线先转动,灯A射线才开始转动,在灯B射线到达之前,设灯A转动t秒,则_________, ________;(用含t的式子表示)
②在①的条件下,若,则________秒.
(3)如图3,若两灯同时转动,在灯A射线到达之前,若射出的光束交于点C,过C作交于点D,且,则在转动过程中,请探究与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
25.已知,直角的边与直线a分别相交于O、G两点,与直线b分别交于E、F点,.
(1)将直角如图1位置摆放,如果,则______;
(2)将直角如图2位置摆放,N为AC上一点,,请写出与之间的等量关系,并说明理由.
(3)将直角如图3位置摆放,若,延长AC交直线b于点Q,点P是射线GF上一动点,探究,与的数量关系,请直接写出结论.
26.已知:直线l分别交AB、CD与E、F两点,且AB∥CD.
(1) 说明:∠1=∠2;
(2) 如图2,点M、N在AB、CD之间,且在直线l左侧,若∠EMN+∠FNM=260°,
①求:∠AEM+∠CFN的度数;
②如图3,若EP平分∠AEM,FP平分∠CFN,求∠P的度数;
(3) 如图4,∠2=80°,点G在射线EB上,点H在AB上方的直线l上,点Q是平面内一点,连接QG、QH,若∠AGQ=18°,∠FHQ=24°,直接写出∠GQH的度数.
27.已知:如图所示,直线MN∥GH,另一直线交GH于A,交MN于B,且∠MBA=80°,点C为直线GH上一动点,点D为直线MN上一动点,且∠GCD=50°.
(1)如图1,当点C在点A右边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(2)如图2,当点C在点A右边且点D在点B右边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(3)当点C在点A左边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线所在直线交于点P,请直接写出∠BPC的度数,不说明理由.
28.直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图①,探究∠AME,∠MEN,∠ENC的数量关系,并说明理由;
(2)如图②,∠AME=30°,EF平分∠MEN,NP平分∠ENC,EQ∥NP,求∠FEQ的度数;
(3)如图③,点G为CD上一点,∠AMN=m∠EMN,∠GEK=m∠GEM,EH∥MN交AB于点H,直接写出∠GEK,∠BMN,∠GEH之间的数量关系(用含m的式子表示).
29.综合与探究,问题情境:综合实践课上,王老师组织同学们开展了探究三角之间数量关系的数学活动.
(1)如图1,,点A,B分别为直线,上的一点,点P为平行线间一点且,,求度数;
问题迁移
(2)如图2,射线与射线交于点O,直线 ,直线m分别交于点A,D,直线n分别交于点B,C,点P在射线上运动.
①当点P在A,B(不与A,B重合)两点之间运动时,设,.则之间有何数量关系?请说明理由;
②若点P不在线段上运动时(点P与点A,B,O三点都不重合),请你直接写出间的数量关系.
答案
一、单选题
1.D
【分析】根据题意,画出图形,不难看出,同位角和内错角的角平分线互相平行.
【解析】如图所示:
,
可得角平分线互相平行的是同位角和内错角.
故选D.
2.C
【分析】直接利用三角板的特点结合根据平行线的性质,计算得,,利用邻补角互补可求得,在中可得到
【解析】∵,
∴,
∵,
∴,
∵,
∴,
∴
在中,,,
∴,
故选:C
3.D
【分析】由题意根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形内角和定理进行计算求解即可.
【解析】解:(1)如图1,由,可得,
∵,
∴.
(2)如图2,过作平行线,则由,
可得,,
∴.
当平分,平分时,
∴,即,
又∵,
∴;
(3)如图3,由,可得,
同理可得:,
∴.
(4)如图4,过E作,由,
∴,
∴,,
∴,
∴.
(5)(6)当点E在的下方时,同理可得,或.
综上所述,的度数可能为,,,,.
故选:D.
4.D
【分析】根据三直线互相平行,可得交点个数;两直线平行与第三条指向相交,可得交点个数;三条直线相交于一点;三条直线两两相交,可得交点个数.
【解析】解:①三直线互相平行,交点个数为0;
②两直线平行与第三条指向相交,交点个数为2个;
③三条直线相交于一点,交点个数为1个;
④三条直线两两相交,交点个数为3个;
故选D.
5.B
【分析】根据两条直线平行的性质:两条直线平行,同位角相等.再根据题意可得两次拐弯的方向不相同,但角度相等.
【解析】解:如图,第一次拐的角是,第二次拐的角是,
由两次拐弯后,还在原来的方向上平行前进得:,
由此可知,两次拐弯的方向不相同,但角度相等,
观察四个选项可知,只有选项B符合,
故选:B.
6.B
【分析】作NE∥AB,MF∥AB,根据两直线平行,内错角相等、同旁内角互补,建立与 的等式即可得到答案.
【解析】如下图所示,作NE∥AB,MF∥AB,
∵AB∥CD,
∴AB∥CD∥MF∥EN
得,,,;
∴,
∵,,
∴,
∴,
∴,
故选:B.
7.B
【分析】首先过点C作,过点D作,由,即可得,然后由两直线平行,内错角相等,即可求得答案.
【解析】解:过点C作,过点D作,
∵,
∴,
∴,
∵,,
由①②得:.
即
故选:B.
8.C
【分析】如图,过点H作,过点F作,根据平行线的性质定理进行解答即可.
【解析】解:如图,过点H作,过点F作,
∴,,
∵,
∴,
∴,
∵, , ,
∴, ,
∴,,
∵,,
∴,
∴,
∵,
∴,
∴,
∴.
故选:C.
9.D
【分析】先设角,利用平行线的性质表示出待求角,再利用整体思想即可求解.
【解析】设
则
∵
∴
∴
故选:D.
10.B
【分析】根据平行线的判定定理得到AD∥BC,故①正确;由平行线的性质得到∠AGK=∠CKG,等量代换得到∠AGK=∠CGK,求得GK平分∠AGC;故②正确;延长EF交AD于P,延长CH交AD于Q,根据平行线的性质和三角形外角的性质得到∠E+∠EAG+∠HCK=180°;故③正确;根据题意列方程得到∠FGA=∠DGH=37°,设∠AGM=α,∠MGK=β,得到∠AGK=α+β,根据角平分线的定义即可得到结论.
【解析】解:∵∠EAD=∠D,∠B=∠D,
∴∠EAD=∠B,
∴AD∥BC,故①正确;
∴∠AGK=∠CKG,
∵∠CKG=∠CGK,
∴∠AGK=∠CGK,
∴GK平分∠AGC;故②正确;
延长EF交AD于P,延长CH交AD于Q,
∵EF∥CH,
∴∠EPQ=∠CQP,
∵∠EPQ=∠E+∠EAG,
∴∠CQG=∠E+∠EAG,
∵AD∥BC,
∴∠HCK+∠CQG=180°,
∴∠E+∠EAG+∠HCK=180°;故③正确;
∵∠FGA的余角比∠DGH大16°,
∴90°-∠FGA-∠DGH=16°,
∵∠FGA=∠DGH,
∴90°-2∠FGA=16°,
∴∠FGA=∠DGH=37°,
设∠AGM=α,∠MGK=β,
∴∠AGK=α+β,
∵GK平分∠AGC,
∴∠CGK=∠AGK=α+β,
∵GM平分∠FGC,
∴∠FGM=∠CGM,
∴∠FGA+∠AGM=∠MGK+∠CGK,
∴37°+α=β+α+β,
∴β=18.5°,
∴∠MGK=18.5°,故④错误,
故选:B.
二、填空题
11.72°
【分析】先根据平行线的判定定理得到ab,然后再利用平行线的性质即可解答.
【解析】解:∵∠4=110°,∠3=70°,
∴∠3+∠4=180°,
∴ab,
∴∠2=∠1=72°.
故答案为:72°.
12.3
【分析】过点作,根据平行线的性质可得,再根据平行线的性质可得,,依此即可求解.
【解析】解:如图,过点作,
∵,
∴,
∴,,,
∴,
∵,,
∴,
∴.
故答案为:3.
13.
【分析】根据得到,再根据即可得到答案.
【解析】解:∵,
∴,
∴,
故答案为:.
14.90°或210°
【分析】OF在运动过程中由两个位置可以使∠AOF=120°,分别作出对应的图像,根据∠AOC的度数以及∠AOE与∠COE间的比例求出两角的值,进而可求出角α的度数.
【解析】解:①当OF运动到如图所示的位置时,
∵∠BOD=75°,
∴∠AOC=∠BOD=75°,
∵ ,
∴,
当时,
∴α=∠AOF-∠AOE=120°-30°=90°,
②如图所示,当OF运动到如图所示的位置时,
∵∠BOD=75°,
∴∠AOC=∠BOD=75°,
∵ ,
∴,
当时,
∴α=360°-(∠AOF+∠AOE)=360°-150°=210°,
故答案为:90°或210°.
15.120
【分析】过E作一条直线,根据题意,得;根据平行线同旁内角互补的性质,推导得,再根据平行线内错角相等的性质计算,即可得到答案.
【解析】解:过E作一条直线,
∵,,
∴,
∵,,
∴,
∴
又∵,
∴.
故答案为:120.
16.或或
【分析】设开启秒后,两灯的光束互相垂直,分,时,灯光返回,第一次与垂直和时,灯光返回,第二次与垂直,三种情况讨论求解即可.
【解析】解:灯P照射一次,需要秒,灯Q照射一次,需要秒,设开启秒后,两灯的光束互相垂直;
①当时,两灯光垂直于点,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
②当时,灯光返回,第一次与垂直,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
③当时,灯光返回,第二次与垂直,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
综上:开启秒或秒或秒时,两灯的光束互相垂直.
17.4
【分析】作EF//AB则AB//CD//EF,根据平行线的性质得出∠MEN=∠BME+∠DME=128°,同理∠ME1N=(∠BME+∠DME) =64°,∠ME2N=(∠BME1+∠DME1) =32°,可归纳规律∠MEnN=(∠BMEn-1+∠DMEn-1) =,依此建立方程=8°求解即可解答.
【解析】解:如图:作EF//AB
∵AB//CD
∴AB//CD//EF
∴∠FEM=∠BME, ∠FEN=∠DNE,
∴∠MEN=∠BME+∠DME=∠FEM +∠FEN =∠MEN= 128°
同理:ME1N=(∠BME+∠DME) =64°,
∠ME2N=(∠BME1+∠DME1) =32°
…
∠MEnN=(∠BMEn-1+∠DMEn-1) =
由题意得:=8°,解得n=4.
故答案为4.
三、解答题
18.(1)解:①如图,直线即为所求作.
②如图,直线即为所求作.
(2)线段的长度是点C到直线的距离,
(3).
理由:垂线段最短.
19.(1)
解:根据题意,利用平行线的性质和判断得,
∵(已知)
∴
∵(已知)
∴FGBC(同位角相等,两直线平行)
∴(两直线平行,内错角相等)
∵(已知)
∴(等量代换)
∴DEBF(同旁内角互补,两直线平行)
∴(两直线平行,同位角相等)
∴(垂直的定义)
故答案是: ; ;两直线平行,内错角相等;;同旁内角互补,两直线平行;两直线平行,同位角相等.
(2)
解:有(1)的结论得,
∵DEBF, , ,
∴ ,
∵
∴,
∴ .
故答案是:.
(3)
解:∵DEBF , ,
∴ , ,
又∵ ,
∴ ,
∴ ,
∴,
故答案是:.
20.解:(1)当∠A、∠C、∠AEC满足条件∠AEC=∠A+∠C时,有ABCD.
理由如下:
过点E作EFAB,如图:
∴∠A=∠1(两直线平行,内错角相等),
∵∠AEC=∠A+∠C,∠AEC=∠1+∠2,
∴∠2=∠C,
∴EFCD(内错角相等,两直线平行),
∵EFAB,
∴ABCD(平行于同一条直线的两条直线互相平行);
故答案为:∠AEC=∠A+∠C;
(2)当ABCD时,∠1,∠2,∠AEC的关系是∠1+∠2-∠AEC=180°,
理由如下:
过点E作EFAB,如图:
∴∠3+∠1=180°(两直线平行,同旁内角互补),
∵ABCD(已知),
∴EFCD(平行于同一条直线的两条直线互相平行),
∴∠FEC=∠2(两直线平行,内错角相等),
即∠AEC+∠3=∠2,
∴∠3=∠2-∠AEC,
∴∠2-∠AEC+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.
故答案为:∠1+∠2-∠AEC=180°.
21.(1)
解:如图①,过点作,
,
(如果一条直线和两条平行线中的一条平行,那么它和另一条也平行).
.
,
.
.
,
.
.
(2)
解:如图②,过点作,
.
,
.
.
,
.
.
.
故答案为:.
(3)
解:如图③,过点作,
,
,
.
,
,
.
.
,
由(2)已得:,
;
平分,
.
平分,
.
,
故答案为:,45.
22.解:(1)过P作PM//AB,过Q作QN//AB,
∵AB//CD,
∴AB//CD//PM,AB//CD//QN,
∴∠BEP=∠MPE,∠DFP=∠MPF,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP=∠MPE+∠MPF=∠EPF=110°,∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=(∠BEP+∠DFP)=×110°=55°;
猜想:∠EPF与∠EQF的数量关系为∠EPF=2∠EQF.理由如下:
∵AB//CD,
∴AB//CD//PM,AB//CD//QN,
∴∠BEP=∠MPE,∠DFP=∠MPF,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP=∠MPE+∠MPF=∠EPF,∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴2(∠BEQ+∠DFQ)=∠BEP+∠DFP=∠EPF,
即∠EPF=2∠EQF;
故答案为:55°;
(2)2∠EQF+∠EPF=360°.理由如下:
如图2,过P作PM//AB,过Q作QN//AB,
∵AB//CD,
∴AB//CD//PM,AB//CD//QN,
∴∠BEP+∠MPE=180°,∠DFP+∠MPF=180°,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP+∠MPE+∠MPF=360°,即∠BEP+∠DFP+∠EPF=360°,∠EQF∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=(∠BEP+∠DFP)=∠EQF,即∠BEP+∠DFP=2∠EQF,
∴2∠EQF+∠EPF=360°;
(3)当点P在EF的左侧,
根据(1)的方法可得∠Q1=(∠BEP+∠DFP)=∠EQF,
∠Q2=(∠BEP+∠DFP)=∠EQF,
…
则∠Qn=()n(∠BEP+∠DFP)=()n∠EQF,
∵2∠EQF+∠EPF=360°,∠BEP+∠DFP=2∠EQF,
∴∠EPF+2n+1 ∠EQnF=360°.
当点P在EF的右侧,同理可求∠EPF=2n+1∠EQnF.
综上,∠EPF+22022 ∠EQ2021F=360°或∠EPF=22022∠EQ2021F.
23.(1)如图1中,
∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴AB∥CD.
(2)结论:如图2中,∠PEQ+2∠PFQ=360°.
理由:作EH∥AB.
∵AB∥CD,EH∥AB,
∴EH∥CD,
∴∠1=∠2,∠3=∠4,
∴∠2+∠3=∠1+∠4,
∴∠PEQ=∠1+∠4,
同法可证:∠PFQ=∠BPF+∠FQD,
∵∠BPE=2∠BPF,∠EQD=2∠FQD,∠1+∠BPE=180°,∠4+∠EQD=180°,
∴∠1+∠4+∠EQD+∠BPE=2×180°,
即∠PEQ+2(∠FQD+∠BPF)=360°,
∴∠PEQ+2∠PFQ=360°.
(3)如图3中,设∠QPF=y,∠PHQ=x.∠EPQ=z,则∠EQF=∠FQH=5y,
∵EQ∥PH,
∴∠EQC=∠PHQ=x,
∴x+10y=180°,
∵AB∥CD,
∴∠BPH=∠PHQ=x,
∵PF平分∠BPE,
∴∠EPQ+∠FPQ=∠FPH+∠BPH,
∴∠FPH=y+z﹣x,
∵PQ平分∠EPH,
∴Z=y+y+z﹣x,
∴x=2y,
∴12y=180°,
∴y=15°,
∴x=30°,
∴∠PHQ=30°.
24.解:(1)∵∠BAM+∠BAN=180°,∠BAM:∠BAN=2:1,
∴∠BAN=180°×=60°,
故答案为:60°;
(2)①由题意可得:,,
故答案为:,;
②设A灯转动t秒,两灯的光束互相平行,
当0<t<90时,如图,
∵PQ∥MN,
∴∠PBD=∠BDA,
∵AC∥BD,
∴∠CAM=∠BDA,
∴∠CAM=∠PBD,
∴2t=1 (30+t),
解得 t=30;
(3)∠BAC和∠BCD关系不会变化.
理由:设灯A射线转动时间为t秒,
∵∠CAN=180°-2t,
∴∠BAC=60°-(180°-2t)=2t-120°,
又∵∠ABC=120°-t,
∴∠BCA=180°-∠ABC-∠BAC=180°-t,而∠ACD=120°,
∴∠BCD=120°-∠BCA=120°-(180°-t)=t-60°,
∴∠BAC:∠BCD=2:1,
即∠BAC=2∠BCD,
∴∠BAC和∠BCD关系不会变化.
25.解:(1)如图1,作CP∥a,
∵,
∴CP∥a∥b,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
∴∠BCP=180°﹣∠CEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+180°﹣∠CEF=90°,
∵∠AOG=46°,
∴∠CEF=136°,
故答案为136°;
(2)∠AOG+∠NEF=90°.
理由如下:如图2,作CP∥a,
则CP∥a∥b,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
而∠NEF+∠CEF=180°,
∴∠BCP=∠NEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+∠NEF=90°;
(3)如图3,当点P在GF上时,过点P作PN∥OG,
∴NP∥OG∥EF,
∴∠GOP=∠OPN,∠PQF=∠NPQ,
∴∠OPQ=∠GOP+∠PQF,
∴∠OPQ=140°﹣∠POQ+∠PQF;
如图4,当点P在线段GF的延长线上时,过点P作PN∥OG,
∴NP∥OG∥EF,
∴∠GOP=∠OPN,∠PQF=∠NPQ,
∵∠OPN=∠OPQ+∠QPN,
∴∠GOP=∠OPQ+∠PQF,
∴140°﹣∠POQ=∠OPQ+∠PQF.
26.(1)
,
;
(2)①分别过点M,N作直线GH,IJ与AB平行,则,如图:
,,,
;
②过点P作AB的平行线,
根据平行线的性质可得:,,
∵EP平分∠AEM,FP平分∠CFN,
∴,
即;
(3)分四种情况进行讨论:
由已知条件可得,
①如图:
②如图:
,
;
③如图:
,
;
④如图:
,
;
综上所述,∠GQH的度数为38°、74°、86°、122°.
27.(1)如图1,过点P作PE∥MN.
∵PB平分∠DBA,
∴∠DBP=∠PBA=40°,
∵PE∥MN,
∴∠BPE=∠DBP=40°,
同理可证:,
∴∠BPC=40°+25°=65°;
(2)如图2,过点P作PE∥MN.
∵∠MBA=80°.
∴∠DBA=180° 80°=100°.
∵BP平分∠DBA.
∴,
∵MN∥PE,
∴∠BPE=180° ∠DBP=130°,
∵PC平分∠DCA.
∴,
∵MN∥PE,MN∥GH,
∴PE∥GH,
∴∠EPC=∠PCA=25°,
∴∠BPC=130°+25°=155°;
(3)如图3,过点P作PE∥MN.
∵BP平分∠DBA.
∴∠DBP=∠PBA=40°,
∵PE∥MN,
∴∠BPE=∠DBP=40°,
∵CP平分∠DCA,∠DCA=180° ∠DCG=130°,
∴,
∵PE∥MN,MN∥GH,
∴PE∥GH,
∴∠CPE=180° ∠PCA=115°,
∴∠BPC=40°+115°=155°.
28.解:(1)过点E作l∥AB,
∵AB∥CD,∴l∥AB∥CD
∴∠1=∠AME,∠2=∠CNE.
∵∠MEN=∠1+∠2,
∴∠MEN=∠AME+∠ENC;
(2)∵EF平分∠MEN,NP平分∠ENC,
∴∠NEF=∠MEN,∠ENP=∠ENC.
∵EQ∥NP,∴∠QEN=∠ENP=∠ENC.
由(1)可得∠MEN=∠AME+∠ENC,∴∠MEN-∠ENC=∠AME=30°.
∴∠FEQ=∠NEF-∠NEQ=(∠MEN-∠ENC)=×30°=15°;
(3)∠BMN+∠GEK-m∠GEH=180°.理由如下:
∵∠AMN=m∠EMN,∠GEK=m∠GEM,
∴∠EMN=∠AMN,∠GEM=∠GEK.
∵EH∥MN,∴∠HEM=∠EMN=∠AMN.
∵∠GEH=∠GEM-∠HEM=∠GEK-∠AMN,
∴m∠GEH=∠GEK-∠AMN.
∵∠BMN+∠AMN=180°,
∴∠BMN+∠GEK-m∠GEH=180°.
29.(1)解: 过P作,如图:
∵,
∴,
∴,,
∴,
即,
∵,,
∴;
(2)解:①,理由如下:
过P作交于E,如图:
∵,
∴,
∴,,
∴ ;
②当P在延长线时,过P作交的延长线于E,如图:
∵,
∴,
∴,,
∴,
此时;
当P在之间时,过P作交的延长线于E,如图:
∵,
∴,
∴,,
∴,
此时.
一、单选题
1.两条平行直线被第三条直线所截时,产生的八个角中,角平分线互相平行的两个角是( ).
A.同位角 B.同旁内角 C.内错角 D.同位角或内错角
2.一副直角三角板如图放置,点C在的延长线上,,,,,则为( )
A. B. C. D.
3.如图,已知直线,被直线所截,,E是平面内任意一点(点E不在直线,,上),设,.下列各式:①,②,③,④,的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
4.平面内三条直线的交点个数可能有〔 〕
A.1个或3个 B.2个或3个
C.1个或2个或3个 D.0个或1个或2个或3
5.一辆汽车在笔直的公路上行驶,两次拐弯后,还在原来的方向上平行前进,那么这两次拐弯的角度应是( )
A.第一次右拐,第二次左拐 B.第一次左拐,第二次右拐
C.第一次左拐,第二次左拐 D.第一次右拐,第二次右拐
6.如图,已知AB∥CD,,.则与之间满足的数量关系是( )
A. B.
C. D.
7.如图,,,探索图中角α,β,γ之间的关系式正确的是( )
A. B. C. D.
8.如图,已知,于点,,,则的度数是( )
A. B. C. D.
9.如图,则与的数量关系是( )
A. B.
C. D.
10.如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EF∥HC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①AD∥BC;②GK平分∠AGC;③∠E+∠EAG+∠HCK=180°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.如图,已知∠1=72°,∠4=110°,∠3=70°,则∠2=____________.
12.如图,,与相交于点,且,,若,则______.
13.如图,,一副三角板(其中,,)按如图所示的位置摆放.若,则的度数为__________(用含的代数式表示).
14.如图,直线相交于点O.已知把分成两个角,且,将射线绕点O逆时针旋转到,若时,的度数是___________.
15.如图,已知,,,则________度.
16.某市拟定在中央公园建设大型灯光秀,在某平行湖道两岸所在直线、安装探照灯,若灯P发出的光束自逆时针旋转至便立即回转,灯Q发出的光束自逆时针旋转至便立即回转,每天晚间两灯同时开启不停交叉照射巡视.设灯P光束转动的速度是10度/秒,灯Q光束转动的速度是4度/秒,在两灯同时开启后的35秒内,开启______秒时,两灯的光束互相垂直.
17.如图,已知直线,点,分别在直线,上,点为,之间一点,且点在的右侧,.若与的平分线相交于点,与的平分线相交于点,与的平分线相交于点……以此类推,若,则的值是______.
三、解答题
18.如图所示的正方形网格,所有小正方形的边长都为1,、、都在格点上.
(1)利用网格作图:
①过点画直线的平行线;
②过点画直线的垂线,垂足为点;
(2)线段的长度是点________到直线________的距离;
(3)比较大小:________(填>、<或=),理由:________.
19.如图,已知,,,试判定 与 的位置关系,并说明理由.
解:.
理由:∵(已知)
∴
∵(已知)
∴______ (同位角相等,两直线平行)
∴______(______)
∵(已知)
∴______ (等量代换)
∴DEBF(______)
∴(______)
∴(垂直的定义)
(1)请补全上面说理过程;
(2)若,求出的度数,并说明理由;
(3)直接写出和的关系______.
20.(1)如图(1),当、、满足条件______时,有ABCD,并说明理由.
(2)如图(2),当ABCD时,,,的关系是______.
21.已知,点为平面内的一点,.
(1)当点在如图①的位置时,求与的数量关系.
解: .(根据如图填射线的画法)
因为,
所以 ( ).
所以(两直线平行,内错角相等);
(请继续完成接下去的说理过程)
(2)当点在如图②的位置时,与的数量关系是 (直接写出答案);
(3)在(2)的条件下,如图③,过点作,垂足为点,与的平分线分别交射线于点、,回答下列问题(直接写出答案):图中与相等的角是 , 度.
22.如图,AB//CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P,且满足0°<∠EPF<180°,QE,QF分别平分∠PEB和∠PFD.在探究∠EPF与∠EQF之间的数量关系时,我们需要对点P的位置进行分类讨论:
(1)如图1,当P点在EF的右侧时,若∠EPF=110°,则∠EQF= ;猜想∠EPF与∠EQF的数量关系,请直接写出结果;
(2)如图2,当P点在EF的左侧时,探究∠EPF与∠EQF的数量关系,请说明理由;
(3)若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3;…以此类推,则∠EPF与∠EQ2021F满足怎样的数量关系?
23.已知:如图(1)直线AB、CD被直线MN所截,∠1=∠2.
(1)求证:AB∥CD;
(2)如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;
(3)如图(3),在(2)的条件下,过P点作PH∥EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.
24.“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯,如图1所示,灯A射线从开始顺时针旋转至便立即回转,灯B射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度,假定主道路是平行的,即,且.
(1)填空:_________;
(2)①若灯B射线先转动,灯A射线才开始转动,在灯B射线到达之前,设灯A转动t秒,则_________, ________;(用含t的式子表示)
②在①的条件下,若,则________秒.
(3)如图3,若两灯同时转动,在灯A射线到达之前,若射出的光束交于点C,过C作交于点D,且,则在转动过程中,请探究与的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
25.已知,直角的边与直线a分别相交于O、G两点,与直线b分别交于E、F点,.
(1)将直角如图1位置摆放,如果,则______;
(2)将直角如图2位置摆放,N为AC上一点,,请写出与之间的等量关系,并说明理由.
(3)将直角如图3位置摆放,若,延长AC交直线b于点Q,点P是射线GF上一动点,探究,与的数量关系,请直接写出结论.
26.已知:直线l分别交AB、CD与E、F两点,且AB∥CD.
(1) 说明:∠1=∠2;
(2) 如图2,点M、N在AB、CD之间,且在直线l左侧,若∠EMN+∠FNM=260°,
①求:∠AEM+∠CFN的度数;
②如图3,若EP平分∠AEM,FP平分∠CFN,求∠P的度数;
(3) 如图4,∠2=80°,点G在射线EB上,点H在AB上方的直线l上,点Q是平面内一点,连接QG、QH,若∠AGQ=18°,∠FHQ=24°,直接写出∠GQH的度数.
27.已知:如图所示,直线MN∥GH,另一直线交GH于A,交MN于B,且∠MBA=80°,点C为直线GH上一动点,点D为直线MN上一动点,且∠GCD=50°.
(1)如图1,当点C在点A右边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(2)如图2,当点C在点A右边且点D在点B右边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(3)当点C在点A左边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线所在直线交于点P,请直接写出∠BPC的度数,不说明理由.
28.直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图①,探究∠AME,∠MEN,∠ENC的数量关系,并说明理由;
(2)如图②,∠AME=30°,EF平分∠MEN,NP平分∠ENC,EQ∥NP,求∠FEQ的度数;
(3)如图③,点G为CD上一点,∠AMN=m∠EMN,∠GEK=m∠GEM,EH∥MN交AB于点H,直接写出∠GEK,∠BMN,∠GEH之间的数量关系(用含m的式子表示).
29.综合与探究,问题情境:综合实践课上,王老师组织同学们开展了探究三角之间数量关系的数学活动.
(1)如图1,,点A,B分别为直线,上的一点,点P为平行线间一点且,,求度数;
问题迁移
(2)如图2,射线与射线交于点O,直线 ,直线m分别交于点A,D,直线n分别交于点B,C,点P在射线上运动.
①当点P在A,B(不与A,B重合)两点之间运动时,设,.则之间有何数量关系?请说明理由;
②若点P不在线段上运动时(点P与点A,B,O三点都不重合),请你直接写出间的数量关系.
答案
一、单选题
1.D
【分析】根据题意,画出图形,不难看出,同位角和内错角的角平分线互相平行.
【解析】如图所示:
,
可得角平分线互相平行的是同位角和内错角.
故选D.
2.C
【分析】直接利用三角板的特点结合根据平行线的性质,计算得,,利用邻补角互补可求得,在中可得到
【解析】∵,
∴,
∵,
∴,
∵,
∴,
∴
在中,,,
∴,
故选:C
3.D
【分析】由题意根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形内角和定理进行计算求解即可.
【解析】解:(1)如图1,由,可得,
∵,
∴.
(2)如图2,过作平行线,则由,
可得,,
∴.
当平分,平分时,
∴,即,
又∵,
∴;
(3)如图3,由,可得,
同理可得:,
∴.
(4)如图4,过E作,由,
∴,
∴,,
∴,
∴.
(5)(6)当点E在的下方时,同理可得,或.
综上所述,的度数可能为,,,,.
故选:D.
4.D
【分析】根据三直线互相平行,可得交点个数;两直线平行与第三条指向相交,可得交点个数;三条直线相交于一点;三条直线两两相交,可得交点个数.
【解析】解:①三直线互相平行,交点个数为0;
②两直线平行与第三条指向相交,交点个数为2个;
③三条直线相交于一点,交点个数为1个;
④三条直线两两相交,交点个数为3个;
故选D.
5.B
【分析】根据两条直线平行的性质:两条直线平行,同位角相等.再根据题意可得两次拐弯的方向不相同,但角度相等.
【解析】解:如图,第一次拐的角是,第二次拐的角是,
由两次拐弯后,还在原来的方向上平行前进得:,
由此可知,两次拐弯的方向不相同,但角度相等,
观察四个选项可知,只有选项B符合,
故选:B.
6.B
【分析】作NE∥AB,MF∥AB,根据两直线平行,内错角相等、同旁内角互补,建立与 的等式即可得到答案.
【解析】如下图所示,作NE∥AB,MF∥AB,
∵AB∥CD,
∴AB∥CD∥MF∥EN
得,,,;
∴,
∵,,
∴,
∴,
∴,
故选:B.
7.B
【分析】首先过点C作,过点D作,由,即可得,然后由两直线平行,内错角相等,即可求得答案.
【解析】解:过点C作,过点D作,
∵,
∴,
∴,
∵,,
由①②得:.
即
故选:B.
8.C
【分析】如图,过点H作,过点F作,根据平行线的性质定理进行解答即可.
【解析】解:如图,过点H作,过点F作,
∴,,
∵,
∴,
∴,
∵, , ,
∴, ,
∴,,
∵,,
∴,
∴,
∵,
∴,
∴,
∴.
故选:C.
9.D
【分析】先设角,利用平行线的性质表示出待求角,再利用整体思想即可求解.
【解析】设
则
∵
∴
∴
故选:D.
10.B
【分析】根据平行线的判定定理得到AD∥BC,故①正确;由平行线的性质得到∠AGK=∠CKG,等量代换得到∠AGK=∠CGK,求得GK平分∠AGC;故②正确;延长EF交AD于P,延长CH交AD于Q,根据平行线的性质和三角形外角的性质得到∠E+∠EAG+∠HCK=180°;故③正确;根据题意列方程得到∠FGA=∠DGH=37°,设∠AGM=α,∠MGK=β,得到∠AGK=α+β,根据角平分线的定义即可得到结论.
【解析】解:∵∠EAD=∠D,∠B=∠D,
∴∠EAD=∠B,
∴AD∥BC,故①正确;
∴∠AGK=∠CKG,
∵∠CKG=∠CGK,
∴∠AGK=∠CGK,
∴GK平分∠AGC;故②正确;
延长EF交AD于P,延长CH交AD于Q,
∵EF∥CH,
∴∠EPQ=∠CQP,
∵∠EPQ=∠E+∠EAG,
∴∠CQG=∠E+∠EAG,
∵AD∥BC,
∴∠HCK+∠CQG=180°,
∴∠E+∠EAG+∠HCK=180°;故③正确;
∵∠FGA的余角比∠DGH大16°,
∴90°-∠FGA-∠DGH=16°,
∵∠FGA=∠DGH,
∴90°-2∠FGA=16°,
∴∠FGA=∠DGH=37°,
设∠AGM=α,∠MGK=β,
∴∠AGK=α+β,
∵GK平分∠AGC,
∴∠CGK=∠AGK=α+β,
∵GM平分∠FGC,
∴∠FGM=∠CGM,
∴∠FGA+∠AGM=∠MGK+∠CGK,
∴37°+α=β+α+β,
∴β=18.5°,
∴∠MGK=18.5°,故④错误,
故选:B.
二、填空题
11.72°
【分析】先根据平行线的判定定理得到ab,然后再利用平行线的性质即可解答.
【解析】解:∵∠4=110°,∠3=70°,
∴∠3+∠4=180°,
∴ab,
∴∠2=∠1=72°.
故答案为:72°.
12.3
【分析】过点作,根据平行线的性质可得,再根据平行线的性质可得,,依此即可求解.
【解析】解:如图,过点作,
∵,
∴,
∴,,,
∴,
∵,,
∴,
∴.
故答案为:3.
13.
【分析】根据得到,再根据即可得到答案.
【解析】解:∵,
∴,
∴,
故答案为:.
14.90°或210°
【分析】OF在运动过程中由两个位置可以使∠AOF=120°,分别作出对应的图像,根据∠AOC的度数以及∠AOE与∠COE间的比例求出两角的值,进而可求出角α的度数.
【解析】解:①当OF运动到如图所示的位置时,
∵∠BOD=75°,
∴∠AOC=∠BOD=75°,
∵ ,
∴,
当时,
∴α=∠AOF-∠AOE=120°-30°=90°,
②如图所示,当OF运动到如图所示的位置时,
∵∠BOD=75°,
∴∠AOC=∠BOD=75°,
∵ ,
∴,
当时,
∴α=360°-(∠AOF+∠AOE)=360°-150°=210°,
故答案为:90°或210°.
15.120
【分析】过E作一条直线,根据题意,得;根据平行线同旁内角互补的性质,推导得,再根据平行线内错角相等的性质计算,即可得到答案.
【解析】解:过E作一条直线,
∵,,
∴,
∵,,
∴,
∴
又∵,
∴.
故答案为:120.
16.或或
【分析】设开启秒后,两灯的光束互相垂直,分,时,灯光返回,第一次与垂直和时,灯光返回,第二次与垂直,三种情况讨论求解即可.
【解析】解:灯P照射一次,需要秒,灯Q照射一次,需要秒,设开启秒后,两灯的光束互相垂直;
①当时,两灯光垂直于点,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
②当时,灯光返回,第一次与垂直,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
③当时,灯光返回,第二次与垂直,过作,如图,
∵,
∴,
∴,,
∴,
解得:;
综上:开启秒或秒或秒时,两灯的光束互相垂直.
17.4
【分析】作EF//AB则AB//CD//EF,根据平行线的性质得出∠MEN=∠BME+∠DME=128°,同理∠ME1N=(∠BME+∠DME) =64°,∠ME2N=(∠BME1+∠DME1) =32°,可归纳规律∠MEnN=(∠BMEn-1+∠DMEn-1) =,依此建立方程=8°求解即可解答.
【解析】解:如图:作EF//AB
∵AB//CD
∴AB//CD//EF
∴∠FEM=∠BME, ∠FEN=∠DNE,
∴∠MEN=∠BME+∠DME=∠FEM +∠FEN =∠MEN= 128°
同理:ME1N=(∠BME+∠DME) =64°,
∠ME2N=(∠BME1+∠DME1) =32°
…
∠MEnN=(∠BMEn-1+∠DMEn-1) =
由题意得:=8°,解得n=4.
故答案为4.
三、解答题
18.(1)解:①如图,直线即为所求作.
②如图,直线即为所求作.
(2)线段的长度是点C到直线的距离,
(3).
理由:垂线段最短.
19.(1)
解:根据题意,利用平行线的性质和判断得,
∵(已知)
∴
∵(已知)
∴FGBC(同位角相等,两直线平行)
∴(两直线平行,内错角相等)
∵(已知)
∴(等量代换)
∴DEBF(同旁内角互补,两直线平行)
∴(两直线平行,同位角相等)
∴(垂直的定义)
故答案是: ; ;两直线平行,内错角相等;;同旁内角互补,两直线平行;两直线平行,同位角相等.
(2)
解:有(1)的结论得,
∵DEBF, , ,
∴ ,
∵
∴,
∴ .
故答案是:.
(3)
解:∵DEBF , ,
∴ , ,
又∵ ,
∴ ,
∴ ,
∴,
故答案是:.
20.解:(1)当∠A、∠C、∠AEC满足条件∠AEC=∠A+∠C时,有ABCD.
理由如下:
过点E作EFAB,如图:
∴∠A=∠1(两直线平行,内错角相等),
∵∠AEC=∠A+∠C,∠AEC=∠1+∠2,
∴∠2=∠C,
∴EFCD(内错角相等,两直线平行),
∵EFAB,
∴ABCD(平行于同一条直线的两条直线互相平行);
故答案为:∠AEC=∠A+∠C;
(2)当ABCD时,∠1,∠2,∠AEC的关系是∠1+∠2-∠AEC=180°,
理由如下:
过点E作EFAB,如图:
∴∠3+∠1=180°(两直线平行,同旁内角互补),
∵ABCD(已知),
∴EFCD(平行于同一条直线的两条直线互相平行),
∴∠FEC=∠2(两直线平行,内错角相等),
即∠AEC+∠3=∠2,
∴∠3=∠2-∠AEC,
∴∠2-∠AEC+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.
故答案为:∠1+∠2-∠AEC=180°.
21.(1)
解:如图①,过点作,
,
(如果一条直线和两条平行线中的一条平行,那么它和另一条也平行).
.
,
.
.
,
.
.
(2)
解:如图②,过点作,
.
,
.
.
,
.
.
.
故答案为:.
(3)
解:如图③,过点作,
,
,
.
,
,
.
.
,
由(2)已得:,
;
平分,
.
平分,
.
,
故答案为:,45.
22.解:(1)过P作PM//AB,过Q作QN//AB,
∵AB//CD,
∴AB//CD//PM,AB//CD//QN,
∴∠BEP=∠MPE,∠DFP=∠MPF,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP=∠MPE+∠MPF=∠EPF=110°,∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=(∠BEP+∠DFP)=×110°=55°;
猜想:∠EPF与∠EQF的数量关系为∠EPF=2∠EQF.理由如下:
∵AB//CD,
∴AB//CD//PM,AB//CD//QN,
∴∠BEP=∠MPE,∠DFP=∠MPF,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP=∠MPE+∠MPF=∠EPF,∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴2(∠BEQ+∠DFQ)=∠BEP+∠DFP=∠EPF,
即∠EPF=2∠EQF;
故答案为:55°;
(2)2∠EQF+∠EPF=360°.理由如下:
如图2,过P作PM//AB,过Q作QN//AB,
∵AB//CD,
∴AB//CD//PM,AB//CD//QN,
∴∠BEP+∠MPE=180°,∠DFP+∠MPF=180°,∠BEQ=∠NQE,∠DFQ=∠FQN,
∴∠BEP+∠DFP+∠MPE+∠MPF=360°,即∠BEP+∠DFP+∠EPF=360°,∠EQF∠BEQ+∠DFQ=∠NQE+∠NQF=∠EQF,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=(∠BEP+∠DFP)=∠EQF,即∠BEP+∠DFP=2∠EQF,
∴2∠EQF+∠EPF=360°;
(3)当点P在EF的左侧,
根据(1)的方法可得∠Q1=(∠BEP+∠DFP)=∠EQF,
∠Q2=(∠BEP+∠DFP)=∠EQF,
…
则∠Qn=()n(∠BEP+∠DFP)=()n∠EQF,
∵2∠EQF+∠EPF=360°,∠BEP+∠DFP=2∠EQF,
∴∠EPF+2n+1 ∠EQnF=360°.
当点P在EF的右侧,同理可求∠EPF=2n+1∠EQnF.
综上,∠EPF+22022 ∠EQ2021F=360°或∠EPF=22022∠EQ2021F.
23.(1)如图1中,
∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴AB∥CD.
(2)结论:如图2中,∠PEQ+2∠PFQ=360°.
理由:作EH∥AB.
∵AB∥CD,EH∥AB,
∴EH∥CD,
∴∠1=∠2,∠3=∠4,
∴∠2+∠3=∠1+∠4,
∴∠PEQ=∠1+∠4,
同法可证:∠PFQ=∠BPF+∠FQD,
∵∠BPE=2∠BPF,∠EQD=2∠FQD,∠1+∠BPE=180°,∠4+∠EQD=180°,
∴∠1+∠4+∠EQD+∠BPE=2×180°,
即∠PEQ+2(∠FQD+∠BPF)=360°,
∴∠PEQ+2∠PFQ=360°.
(3)如图3中,设∠QPF=y,∠PHQ=x.∠EPQ=z,则∠EQF=∠FQH=5y,
∵EQ∥PH,
∴∠EQC=∠PHQ=x,
∴x+10y=180°,
∵AB∥CD,
∴∠BPH=∠PHQ=x,
∵PF平分∠BPE,
∴∠EPQ+∠FPQ=∠FPH+∠BPH,
∴∠FPH=y+z﹣x,
∵PQ平分∠EPH,
∴Z=y+y+z﹣x,
∴x=2y,
∴12y=180°,
∴y=15°,
∴x=30°,
∴∠PHQ=30°.
24.解:(1)∵∠BAM+∠BAN=180°,∠BAM:∠BAN=2:1,
∴∠BAN=180°×=60°,
故答案为:60°;
(2)①由题意可得:,,
故答案为:,;
②设A灯转动t秒,两灯的光束互相平行,
当0<t<90时,如图,
∵PQ∥MN,
∴∠PBD=∠BDA,
∵AC∥BD,
∴∠CAM=∠BDA,
∴∠CAM=∠PBD,
∴2t=1 (30+t),
解得 t=30;
(3)∠BAC和∠BCD关系不会变化.
理由:设灯A射线转动时间为t秒,
∵∠CAN=180°-2t,
∴∠BAC=60°-(180°-2t)=2t-120°,
又∵∠ABC=120°-t,
∴∠BCA=180°-∠ABC-∠BAC=180°-t,而∠ACD=120°,
∴∠BCD=120°-∠BCA=120°-(180°-t)=t-60°,
∴∠BAC:∠BCD=2:1,
即∠BAC=2∠BCD,
∴∠BAC和∠BCD关系不会变化.
25.解:(1)如图1,作CP∥a,
∵,
∴CP∥a∥b,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
∴∠BCP=180°﹣∠CEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+180°﹣∠CEF=90°,
∵∠AOG=46°,
∴∠CEF=136°,
故答案为136°;
(2)∠AOG+∠NEF=90°.
理由如下:如图2,作CP∥a,
则CP∥a∥b,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
而∠NEF+∠CEF=180°,
∴∠BCP=∠NEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+∠NEF=90°;
(3)如图3,当点P在GF上时,过点P作PN∥OG,
∴NP∥OG∥EF,
∴∠GOP=∠OPN,∠PQF=∠NPQ,
∴∠OPQ=∠GOP+∠PQF,
∴∠OPQ=140°﹣∠POQ+∠PQF;
如图4,当点P在线段GF的延长线上时,过点P作PN∥OG,
∴NP∥OG∥EF,
∴∠GOP=∠OPN,∠PQF=∠NPQ,
∵∠OPN=∠OPQ+∠QPN,
∴∠GOP=∠OPQ+∠PQF,
∴140°﹣∠POQ=∠OPQ+∠PQF.
26.(1)
,
;
(2)①分别过点M,N作直线GH,IJ与AB平行,则,如图:
,,,
;
②过点P作AB的平行线,
根据平行线的性质可得:,,
∵EP平分∠AEM,FP平分∠CFN,
∴,
即;
(3)分四种情况进行讨论:
由已知条件可得,
①如图:
②如图:
,
;
③如图:
,
;
④如图:
,
;
综上所述,∠GQH的度数为38°、74°、86°、122°.
27.(1)如图1,过点P作PE∥MN.
∵PB平分∠DBA,
∴∠DBP=∠PBA=40°,
∵PE∥MN,
∴∠BPE=∠DBP=40°,
同理可证:,
∴∠BPC=40°+25°=65°;
(2)如图2,过点P作PE∥MN.
∵∠MBA=80°.
∴∠DBA=180° 80°=100°.
∵BP平分∠DBA.
∴,
∵MN∥PE,
∴∠BPE=180° ∠DBP=130°,
∵PC平分∠DCA.
∴,
∵MN∥PE,MN∥GH,
∴PE∥GH,
∴∠EPC=∠PCA=25°,
∴∠BPC=130°+25°=155°;
(3)如图3,过点P作PE∥MN.
∵BP平分∠DBA.
∴∠DBP=∠PBA=40°,
∵PE∥MN,
∴∠BPE=∠DBP=40°,
∵CP平分∠DCA,∠DCA=180° ∠DCG=130°,
∴,
∵PE∥MN,MN∥GH,
∴PE∥GH,
∴∠CPE=180° ∠PCA=115°,
∴∠BPC=40°+115°=155°.
28.解:(1)过点E作l∥AB,
∵AB∥CD,∴l∥AB∥CD
∴∠1=∠AME,∠2=∠CNE.
∵∠MEN=∠1+∠2,
∴∠MEN=∠AME+∠ENC;
(2)∵EF平分∠MEN,NP平分∠ENC,
∴∠NEF=∠MEN,∠ENP=∠ENC.
∵EQ∥NP,∴∠QEN=∠ENP=∠ENC.
由(1)可得∠MEN=∠AME+∠ENC,∴∠MEN-∠ENC=∠AME=30°.
∴∠FEQ=∠NEF-∠NEQ=(∠MEN-∠ENC)=×30°=15°;
(3)∠BMN+∠GEK-m∠GEH=180°.理由如下:
∵∠AMN=m∠EMN,∠GEK=m∠GEM,
∴∠EMN=∠AMN,∠GEM=∠GEK.
∵EH∥MN,∴∠HEM=∠EMN=∠AMN.
∵∠GEH=∠GEM-∠HEM=∠GEK-∠AMN,
∴m∠GEH=∠GEK-∠AMN.
∵∠BMN+∠AMN=180°,
∴∠BMN+∠GEK-m∠GEH=180°.
29.(1)解: 过P作,如图:
∵,
∴,
∴,,
∴,
即,
∵,,
∴;
(2)解:①,理由如下:
过P作交于E,如图:
∵,
∴,
∴,,
∴ ;
②当P在延长线时,过P作交的延长线于E,如图:
∵,
∴,
∴,,
∴,
此时;
当P在之间时,过P作交的延长线于E,如图:
∵,
∴,
∴,,
∴,
此时.
