第5章 生活中的轴对称(单元测试·基础卷)(含解析)
文档属性
| 名称 | 第5章 生活中的轴对称(单元测试·基础卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 20:40:58 | ||
图片预览


文档简介
第5章 生活中的轴对称(单元测试·基础卷)
【要点回顾】
【知识点1】轴对称图形
(1)如果一个图形沿一条直线折叠后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
(2)线段、角、长方形、正方形、等腰三角形、圆都是轴对称图形;
(3)对称轴是直线而不是线段;
【知识点2】轴对称
轴对称:对于两个图形,如果沿一条直线对折后,它们能互相重合,那么称这两个图形成轴对称,这条直线就是对称轴。可以说成:这两个图形关于某条直线对称。
轴对称与轴对称图形的区别与联系:
轴对称图形 轴对称
区别 是一个图形自身的对称特性 是两个图形之间的对称关系
对称轴可能不止一条 对称轴只有一条
共同点 沿某条直线对折后都能够互相重合
如果轴对称的两个图形看作一个整体,那么它就是一个轴对称图形; 如果把轴对称图形分成两部分(两个图形),那么这两部分关于这条对称轴成轴对称。
【知识点3】角平分线的性质
(1)角平分线所在的直线是该角的对称轴。
(2)性质:角平分线上的点到这个角的两边的距离相等。(距离强调垂直)
【知识点4】线段的垂直平分线
(1)线段的垂直平分线:垂直于一条线段并且平分这条线段的直线叫做这条线段的垂直平分线,又叫线段的中垂线。
(2)性质:线段垂直平分线上的点到这条线段两端点的距离相等。
【知识点5】等腰三角形
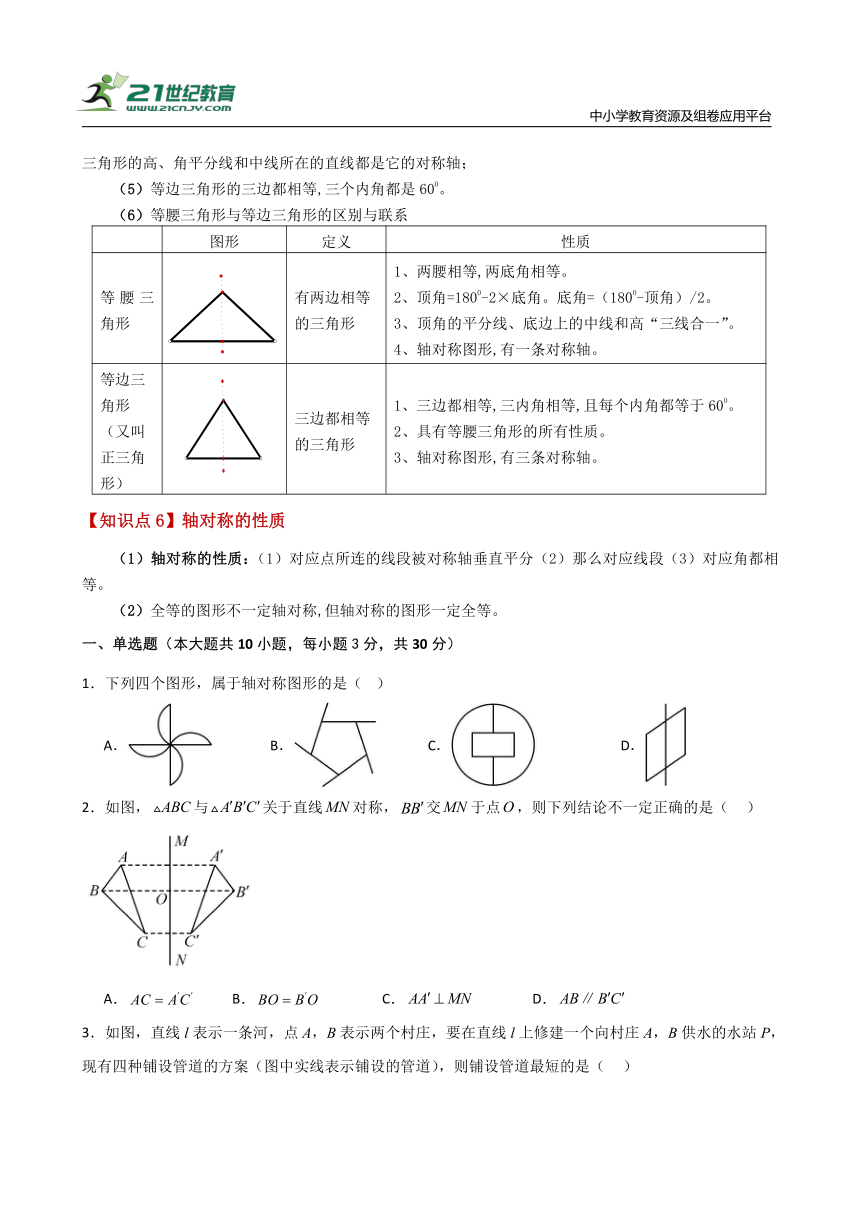
(1)等腰三角形:等腰三角形是轴对称图形,有一条对称轴(等边三角形除外),其底边上的高或顶角的平分线,或底边上的中线所在的直线都是它的对称轴;
(2)三线合一:等腰三角形底边上的高,底边上的中线,顶角的平分线互相重合,简称为“三线合一”;
(3)等腰三角形的两个底角相等,简写成“等边对等角”;
(4)等边三角形:等边三角形是指三边都相等的三角形,又称正三角形,等边三角形有三条对称轴,三角形的高、角平分线和中线所在的直线都是它的对称轴;
(5)等边三角形的三边都相等,三个内角都是600。
(6)等腰三角形与等边三角形的区别与联系
图形 定义 性质
等腰三角形 有两边相等的三角形 1、两腰相等,两底角相等。 2、顶角=1800-2×底角。底角=(1800-顶角)/2。 3、顶角的平分线、底边上的中线和高“三线合一”。 4、轴对称图形,有一条对称轴。
等边三角形(又叫正三角形) 三边都相等的三角形 1、三边都相等,三内角相等,且每个内角都等于600。 2、具有等腰三角形的所有性质。 3、轴对称图形,有三条对称轴。
【知识点6】轴对称的性质
(1)轴对称的性质:(1)对应点所连的线段被对称轴垂直平分(2)那么对应线段(3)对应角都相等。
(2)全等的图形不一定轴对称,但轴对称的图形一定全等。
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列四个图形,属于轴对称图形的是( )
A. B. C. D.
2.如图,与关于直线对称,交于点,则下列结论不一定正确的是( )
A. B. C. D.
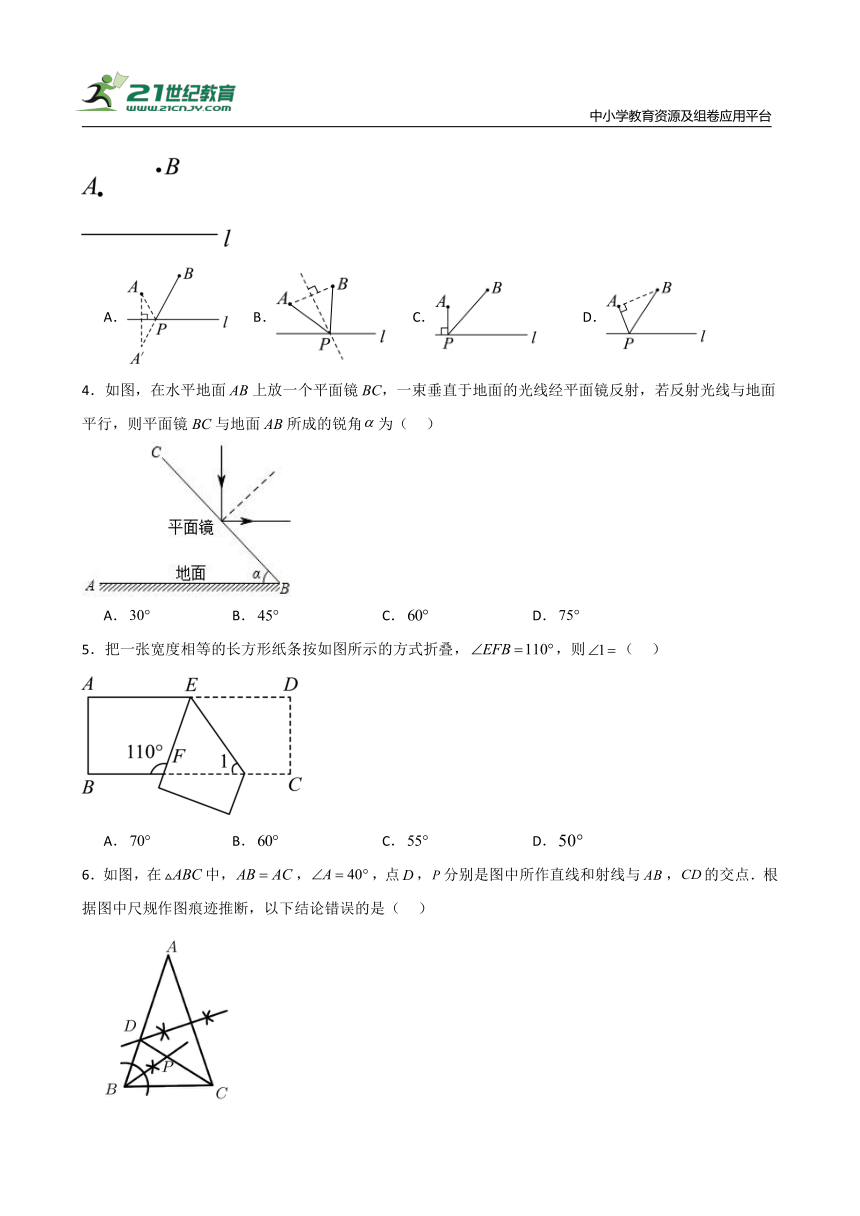
3.如图,直线l表示一条河,点A,B表示两个村庄,要在直线l上修建一个向村庄A,B供水的水站P,现有四种铺设管道的方案(图中实线表示铺设的管道),则铺设管道最短的是( )
A. B. C. D.
4.如图,在水平地面AB上放一个平面镜BC,一束垂直于地面的光线经平面镜反射,若反射光线与地面平行,则平面镜BC与地面AB所成的锐角为( )
A. B. C. D.
5.把一张宽度相等的长方形纸条按如图所示的方式折叠,,则( )
A. B. C. D.
6.如图,在中,,,点,分别是图中所作直线和射线与,的交点.根据图中尺规作图痕迹推断,以下结论错误的是( )
A. B. C. D.
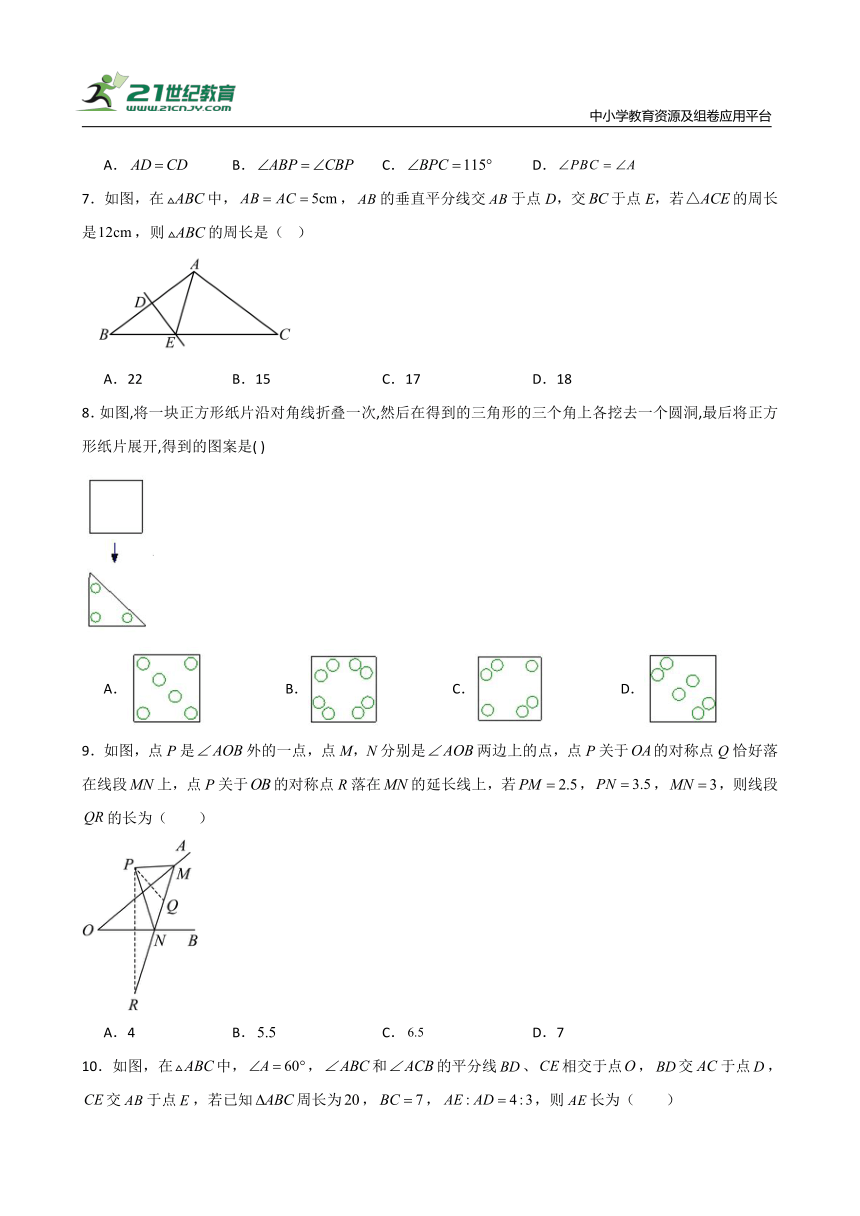
7.如图,在中,,的垂直平分线交于点D,交于点E,若的周长是,则的周长是( )
A.22 B.15 C.17 D.18
8.如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )
A. B. C. D.
9.如图,点P是外的一点,点M,N分别是两边上的点,点P关于的对称点Q恰好落在线段上,点P关于的对称点R落在的延长线上,若,,,则线段的长为( )
A.4 B. C. D.7
10.如图,在中,,和的平分线、相交于点,交于点,交于点,若已知周长为,,,则长为( )
A. B. C. D.4
二、填空题(本大题共8小题,每小题4分,共32分)
11.角是轴对称图形, 是它的对称轴.
12.如图,在中,点D,E分别在边,上,点A与点E关于直线对称.若,,,则的周长为 .
13.如图,将长方形纸片沿直线折叠.若,则 .
14.如图,,点M,N分别是边,上的定点,点P,Q分别是边,上的动点,记,,当的值最小时,的大小_______(度).
15.如图,在中,,,,垂直平分,点D为直线上的任意一点,则周长的最小值是 .
16.如图,在中,平分交于点为上一点,且.若,则 .
17.已知等腰三角形的周长为12,底边长为5,则腰长为 .
18.如图,在五边形中,,在上分别找到一点,使得的周长最小,则的度数为 .
三、解答题(本大题共6小题,共58分)
19.(8分)19.如图,在中,,,点D,E分别是线段和线段上的点,连接,和关于所在直线对称,连接交于点F.求的度数.
20.(8分)如图,已知ABC.
(1)尺规作图:作∠BAC的角平分线交BC于点D,作∠ABC的角平分线交AC于点,且AD、BE交于点O(保留作图痕迹)
(2)连接,若AB=6,BC=4,AC=8,求的比值.
21.(10分)已知:如图,在ABC中,AB=AC,AB的垂直平分线DE交AC于点D,交AB于点E,∠C=75°.
(1) 求∠A的度数; (2) 求∠CBD的度数.
22.(10分)如图,在△ABC中,AB=AC,AC边上的高BD=4, P为BC上一点,PE⊥AC于E.PF⊥AB于F,求PE+PF的值.
23.(10分)如图,和关于直线对称,与的交点在直线上.
(1) 图中点的对应点是点______,的对应边是______;
(2) 若,,求的度数.
24.(12分)阅读并理解下面内容,解答问题.
三角形的内心
定义:三角形的三条内角平分线相交于一点,这个点叫做三角形的内心.
如图1,已知AM,BN,CP是△ABC的三条内角平分线.
求证:AM,BN,CP相交于一点.
证明:如图2,设AM,BN相交于点O,
过点O分别作,,,垂足分别为点D,E,F.
∵点O是∠BAC的平分线AM上的一点,
∴,(依据1)
同理,.
∴.(依据2)
∵CP是∠ACB的平分线,
∴点O在CP上,(依据3)
∴AM,BN,CP相交于一点.
请解答以下问题:
(1)上述证明过程中的“依据1”“依据2”“依据3”分别是指什么?
(2)如果,,,,请直接用a,b,c,r表示△ABC的面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.C
【分析】本题考查轴对称图形,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,由此即可判断.
【详解】解:A.选项中的图形不是轴对称图形,故此选项不符合题意;
B.选项中的图形不是轴对称图形,故此选项不符合题意;
C.图形是轴对称图形.故C符合题意.
D.选项中的图形不是轴对称图形,故此选项不符合题意;
故选:C.
2.D
【分析】本题主要考查轴对称图形的性质,全等三角形的性质,掌握轴对称与图形对应点的连线相互垂直平分是解题的关键.根据轴对称图形的性质即可求解.
【详解】解:与关于直线对称,
∴,
∴,故选项正确,不符合题意;
∵与关于直线对称,交于点,
∴,,
故、选项正确,不符合题意;
与,不一定平行,故选项错误,符合题意;
故选:.
3.A
【分析】本题天考查了轴对称最短路线问题,能正确画出图形是解此题的关键.先作点关于直线的对称点,再连接,即可得出答案.
【详解】解:如图,作关于直线的对称点,连接交直线于点,则此时为所求,
故选:A.
4.B
【分析】利用平行线的性质和光的反射原理计算.
【详解】解:入射光线垂直于水平光线,
它们的夹角为90°,虚线为法线,为入射角,
两水平线平行
故选:B.
【点拨】本题考查平行线的性质、光的反射原理、入射角等于反射角等知识,是基础考点,掌握相关知识是解题关键.
5.C
【分析】本题考查的是折叠的性质,平行线的性质,根据折叠的性质可得,再证明,再结合平行线的性质可得结论.
【详解】如图,
根据折叠得出,
∵纸条是一张宽度相等的纸条,
∴,
∴,,
又,
∴,
故选:C.
6.D
【分析】根据角平分线的定义和垂直平分线的性质判断A、B,再根据等腰三角形的性质和三角形的内角定理判断C、D.
【详解】解:根据图中尺规作图可知,AC的垂直平分线交AB于D,BP平分∠ABC,
∴,;选项A、B正确;
∵,
∴∠ACD=∠A =40°,
∵,,
∴∠ABC=∠ACB =70°,
∴,选项D错误;
∴∠BPC=180°-∠CBP-∠BCP =115°,选项C正确;
故选:D
【点拨】本题考查了基本作图,垂直平分线的性质,角平分线的定义,等腰三角形的性质,熟练掌握相关的知识是解题的关键
7.C
【分析】由的垂直平分线交于点D,交于点E,易得,又由的周长是,可求得,继而求得答案.
【详解】解:∵是的垂直平分线,
∴,
∵的周长是,
∴,
∵,
∴的周长是:.
故选:C.
【点拨】此题考查了线段垂直平分线的性质.此题难度不大,注意转化思想与数形结合思想的应用.
8.C
【详解】此题主要考查学生的动手实践能力和想象能力
由平面图形的折叠的特点结合实际操作解题.
通过自己动手,亲自实践一下,很容易得出正确结果为C.故选C.
9.A
【分析】本题考查了轴对称的性质:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.根据轴对称的性质可求、的长度,然后根据线段的和差求解即可.
【详解】解:∵点关于的对称点恰好落在线段上,,
∴,
同理,
又∵,
∴.
故选:A.
10.B
【分析】本题考查了全等三角形的判定和性质,角平分线的性质,添加恰当辅助线构造全等三角形是解题的关键.
【详解】解:如图,在上截取,连接,
平分,平分,
,,
,
,
,
,
,
在和中,
,
,
,
,
在和中,
,
,
,
,
周长为20,
,
,
,
.
故选:B.
11.角平分线所在的直线
【分析】根据角平分线的定义即可解答.
【详解】解:角的对称轴是“角平分线所在的直线”.
故答案为:角平分线所在的直线.
【点拨】本题主要考查了轴对称图形,理解轴对称图形沿对称轴折叠能够完全重合是解题的关键.
12.11
【分析】本题主要考查了轴对称的性质.根据轴对称的性质可得,,进而得出,再根据三角形的周长公式,即可求解.
【详解】解:∵点A与点E关于直线对称,
∴,,
∵,
∴,
∴的周长.
故答案为:11.
13./100度
【分析】本题主要考查了正方形的性质以及折叠的性质,由正方形的性质得出,由平行的性质得出,由叠的性质可知:,再由平角的定义即可求出.
【详解】解:∵是正方形,
∴,
∴,
由折叠的性质可知:,
∴,
故答案为:.
14.50
【分析】本题主要考查最短路径问题、轴对称的性质,三角形外角的性质,作M关于的对称点,N关于的对称点,连接,交于点P,交于点Q,连接,,可知此时最小,此时,,再根据三角形外角的性质和平角的定义即可得出结论.
【详解】解:作M关于的对称点,N关于的对称点,连接,交于点P,交于点Q,连接,,如图所示.
根据两点之间,线段最短,可知此时最小,即,
∴,,
∵,,
∴,,
∵,,
∴,
∴,
故答案为:50.
15.10
【分析】本题考查了轴对称最短路线问题的应用,垂直平分线的性质,准确找出点D的位置是解答本题的关键.根据垂直平分线的性质可知,点B与点C关于对称,故当点D与点P重合时,的值最小,最小值等于的长,由此即可得到答案.
【详解】垂直平分,
点B与点C关于对称,
如图,设与相较于点P,
当点D与点P重合时,的值最小,最小值等于的长,
,,
周长的最小值是,
故答案为:10.
16.
【分析】过D作DF⊥BC于F,依据角平分线的性质,即可得到AD=FD,再根据S△BCD=26,即可得出DF的长,进而得到AD的长.
【详解】如图,过D作DF⊥BC于F,
∵∠A=90°,CD平分∠ACB,
∴AD=FD,
∵S△BCD=26,BC=13,
∴×13×DF=26,
∴DF=4,AD=4.
故答案为:4.
【点拨】本题主要考查了角平分线的性质以及平行线的判定,角的平分线上的点到角的两边的距离相等.
17.3.5
【分析】根据等腰三角形的性质计算即可;
【详解】设等腰三角形的一条腰为x,
∵腰三角形的周长为12,底边长为5,
∴,
解得;
故答案是3.5.
【点拨】本题主要考查了等腰三角形的性质,准确分析计算是解题的关键.
18.120°
【分析】此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.根据要使的周长最小,即利用点的对称,让三角形的三边在同一直线上,A关于和的对称点,,即可得出,进而得出即可得出答案.
【详解】解:作关于和的对称点,,连接,,交于M,交于N,则即为的周长最小值.作延长线,
∵,
∴,
∴,
∵,,
且,,
∴,
故答案为:.
19.
【分析】本题考查了对称的性质、三角形的外角定理等知识,根据对称有,,从而,,可先求出的度数,然后根据外角,进而求出的度数,从而求解.
【详解】解:∵和关于直线对称,
∴,,
∴,.
∵,
∴.
又∵
∴
∴
20.(1)见解析;(2)3:2:4
【分析】(1)依据题干要求作出图形即可;
(2)根据角平分线的性质可得△ABO中AB边上的高和△ACO中AC边上的高以及△BCO中BC边上的高相等,从而得到的比值等于AB:AC:BC.
【详解】解:(1)如图,即为所作图形;
(2)∵AO平分∠BAC,BE平分∠ABC,
∴OC平分∠ACB,
∴点O到AB、BC和AC的距离相等,
即△ABO中AB边上的高和△ACO中AC边上的高以及△BCO中BC边上的高相等,
∵AB=6,BC=4,AC=8,
∴=AB:AC:BC=6:4:8=3:2:4.
【点拨】本题考查了尺规作图,角平分线的性质,解题的关键是根据角平分线的性质得到三角形的高相等.
21.(1)∠A的度数30°;
(2)∠CBD的度数为45°
【分析】(1)根据等腰三角形的性质、三角形内角和定理即可求出∠A的度数;
(2)根据线段垂直平分线的性质得到DA=DB,得到∠DBA=∠A,再计算即可.
【详解】(1)解:∵AB=AC,∠C=75°,
∴∠ABC=∠C=75°,
∴∠A=180°-75°-75°=30°,
∴∠A的度数30°;
(2)解:∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DBA=∠A=30°,
∴∠CBD=∠ABC-∠ABD=75°-30°=45°,
∴∠CBD的度数为45°.
【点拨】本题考查了线段垂直平分线、等腰三角形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
22.4
【分析】连接AP,根据和AB=AC,即可得.
【详解】解:如图所示,连接AP,
∴,
∵AB=AC,
∴,
∵,
∴,
∴,
【点拨】本题考查了等腰三角形的性质,解题的关键是知道三角形ABC,三角形ABP,三角形ACP面积之间的关系.
23.(1),
(2)
【分析】本题主要考查了轴对称的性质,解题的关键是熟练掌握性质,准确计算.
(1)本题考查轴对称的性质,根据轴对称的性质解答即可.
(2)本题根据轴对称性质推出,从而得出,最后根据即可解题.
【详解】(1)解:由题意可得:图中点的对应点是点,的对应边是,
故答案为:,.
(2)解:,
,
,
.
24.(1)依据1:角平分线上的点到角的两边的距离相等;依据2:等量代换;依据3:角的内部到角的两边距离相等的点在这个角的平分线上;(2)或.
【分析】(1)根据题意可直接进行作答;
(2)由(1)可得OD=OE=OF,然后根据等积法进行求解即可.
【详解】解:(1)由题意得:
依据1:角平分线上的点到角的两边的距离相等.
依据2:等量代换.
依据3:角的内部到角的两边距离相等的点在这个角的平分线上.
(2)由(1)得:
OD=OE=OF=r,
,,,
,
△ABC的面积表示为:.
【点拨】本题主要考查角平分线的性质定理及判定定理,熟练掌握角平分线的性质定理及判定定理是解题的关键.
【要点回顾】
【知识点1】轴对称图形
(1)如果一个图形沿一条直线折叠后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
(2)线段、角、长方形、正方形、等腰三角形、圆都是轴对称图形;
(3)对称轴是直线而不是线段;
【知识点2】轴对称
轴对称:对于两个图形,如果沿一条直线对折后,它们能互相重合,那么称这两个图形成轴对称,这条直线就是对称轴。可以说成:这两个图形关于某条直线对称。
轴对称与轴对称图形的区别与联系:
轴对称图形 轴对称
区别 是一个图形自身的对称特性 是两个图形之间的对称关系
对称轴可能不止一条 对称轴只有一条
共同点 沿某条直线对折后都能够互相重合
如果轴对称的两个图形看作一个整体,那么它就是一个轴对称图形; 如果把轴对称图形分成两部分(两个图形),那么这两部分关于这条对称轴成轴对称。
【知识点3】角平分线的性质
(1)角平分线所在的直线是该角的对称轴。
(2)性质:角平分线上的点到这个角的两边的距离相等。(距离强调垂直)
【知识点4】线段的垂直平分线
(1)线段的垂直平分线:垂直于一条线段并且平分这条线段的直线叫做这条线段的垂直平分线,又叫线段的中垂线。
(2)性质:线段垂直平分线上的点到这条线段两端点的距离相等。
【知识点5】等腰三角形
(1)等腰三角形:等腰三角形是轴对称图形,有一条对称轴(等边三角形除外),其底边上的高或顶角的平分线,或底边上的中线所在的直线都是它的对称轴;
(2)三线合一:等腰三角形底边上的高,底边上的中线,顶角的平分线互相重合,简称为“三线合一”;
(3)等腰三角形的两个底角相等,简写成“等边对等角”;
(4)等边三角形:等边三角形是指三边都相等的三角形,又称正三角形,等边三角形有三条对称轴,三角形的高、角平分线和中线所在的直线都是它的对称轴;
(5)等边三角形的三边都相等,三个内角都是600。
(6)等腰三角形与等边三角形的区别与联系
图形 定义 性质
等腰三角形 有两边相等的三角形 1、两腰相等,两底角相等。 2、顶角=1800-2×底角。底角=(1800-顶角)/2。 3、顶角的平分线、底边上的中线和高“三线合一”。 4、轴对称图形,有一条对称轴。
等边三角形(又叫正三角形) 三边都相等的三角形 1、三边都相等,三内角相等,且每个内角都等于600。 2、具有等腰三角形的所有性质。 3、轴对称图形,有三条对称轴。
【知识点6】轴对称的性质
(1)轴对称的性质:(1)对应点所连的线段被对称轴垂直平分(2)那么对应线段(3)对应角都相等。
(2)全等的图形不一定轴对称,但轴对称的图形一定全等。
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列四个图形,属于轴对称图形的是( )
A. B. C. D.
2.如图,与关于直线对称,交于点,则下列结论不一定正确的是( )
A. B. C. D.
3.如图,直线l表示一条河,点A,B表示两个村庄,要在直线l上修建一个向村庄A,B供水的水站P,现有四种铺设管道的方案(图中实线表示铺设的管道),则铺设管道最短的是( )
A. B. C. D.
4.如图,在水平地面AB上放一个平面镜BC,一束垂直于地面的光线经平面镜反射,若反射光线与地面平行,则平面镜BC与地面AB所成的锐角为( )
A. B. C. D.
5.把一张宽度相等的长方形纸条按如图所示的方式折叠,,则( )
A. B. C. D.
6.如图,在中,,,点,分别是图中所作直线和射线与,的交点.根据图中尺规作图痕迹推断,以下结论错误的是( )
A. B. C. D.
7.如图,在中,,的垂直平分线交于点D,交于点E,若的周长是,则的周长是( )
A.22 B.15 C.17 D.18
8.如图,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )
A. B. C. D.
9.如图,点P是外的一点,点M,N分别是两边上的点,点P关于的对称点Q恰好落在线段上,点P关于的对称点R落在的延长线上,若,,,则线段的长为( )
A.4 B. C. D.7
10.如图,在中,,和的平分线、相交于点,交于点,交于点,若已知周长为,,,则长为( )
A. B. C. D.4
二、填空题(本大题共8小题,每小题4分,共32分)
11.角是轴对称图形, 是它的对称轴.
12.如图,在中,点D,E分别在边,上,点A与点E关于直线对称.若,,,则的周长为 .
13.如图,将长方形纸片沿直线折叠.若,则 .
14.如图,,点M,N分别是边,上的定点,点P,Q分别是边,上的动点,记,,当的值最小时,的大小_______(度).
15.如图,在中,,,,垂直平分,点D为直线上的任意一点,则周长的最小值是 .
16.如图,在中,平分交于点为上一点,且.若,则 .
17.已知等腰三角形的周长为12,底边长为5,则腰长为 .
18.如图,在五边形中,,在上分别找到一点,使得的周长最小,则的度数为 .
三、解答题(本大题共6小题,共58分)
19.(8分)19.如图,在中,,,点D,E分别是线段和线段上的点,连接,和关于所在直线对称,连接交于点F.求的度数.
20.(8分)如图,已知ABC.
(1)尺规作图:作∠BAC的角平分线交BC于点D,作∠ABC的角平分线交AC于点,且AD、BE交于点O(保留作图痕迹)
(2)连接,若AB=6,BC=4,AC=8,求的比值.
21.(10分)已知:如图,在ABC中,AB=AC,AB的垂直平分线DE交AC于点D,交AB于点E,∠C=75°.
(1) 求∠A的度数; (2) 求∠CBD的度数.
22.(10分)如图,在△ABC中,AB=AC,AC边上的高BD=4, P为BC上一点,PE⊥AC于E.PF⊥AB于F,求PE+PF的值.
23.(10分)如图,和关于直线对称,与的交点在直线上.
(1) 图中点的对应点是点______,的对应边是______;
(2) 若,,求的度数.
24.(12分)阅读并理解下面内容,解答问题.
三角形的内心
定义:三角形的三条内角平分线相交于一点,这个点叫做三角形的内心.
如图1,已知AM,BN,CP是△ABC的三条内角平分线.
求证:AM,BN,CP相交于一点.
证明:如图2,设AM,BN相交于点O,
过点O分别作,,,垂足分别为点D,E,F.
∵点O是∠BAC的平分线AM上的一点,
∴,(依据1)
同理,.
∴.(依据2)
∵CP是∠ACB的平分线,
∴点O在CP上,(依据3)
∴AM,BN,CP相交于一点.
请解答以下问题:
(1)上述证明过程中的“依据1”“依据2”“依据3”分别是指什么?
(2)如果,,,,请直接用a,b,c,r表示△ABC的面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.C
【分析】本题考查轴对称图形,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,由此即可判断.
【详解】解:A.选项中的图形不是轴对称图形,故此选项不符合题意;
B.选项中的图形不是轴对称图形,故此选项不符合题意;
C.图形是轴对称图形.故C符合题意.
D.选项中的图形不是轴对称图形,故此选项不符合题意;
故选:C.
2.D
【分析】本题主要考查轴对称图形的性质,全等三角形的性质,掌握轴对称与图形对应点的连线相互垂直平分是解题的关键.根据轴对称图形的性质即可求解.
【详解】解:与关于直线对称,
∴,
∴,故选项正确,不符合题意;
∵与关于直线对称,交于点,
∴,,
故、选项正确,不符合题意;
与,不一定平行,故选项错误,符合题意;
故选:.
3.A
【分析】本题天考查了轴对称最短路线问题,能正确画出图形是解此题的关键.先作点关于直线的对称点,再连接,即可得出答案.
【详解】解:如图,作关于直线的对称点,连接交直线于点,则此时为所求,
故选:A.
4.B
【分析】利用平行线的性质和光的反射原理计算.
【详解】解:入射光线垂直于水平光线,
它们的夹角为90°,虚线为法线,为入射角,
两水平线平行
故选:B.
【点拨】本题考查平行线的性质、光的反射原理、入射角等于反射角等知识,是基础考点,掌握相关知识是解题关键.
5.C
【分析】本题考查的是折叠的性质,平行线的性质,根据折叠的性质可得,再证明,再结合平行线的性质可得结论.
【详解】如图,
根据折叠得出,
∵纸条是一张宽度相等的纸条,
∴,
∴,,
又,
∴,
故选:C.
6.D
【分析】根据角平分线的定义和垂直平分线的性质判断A、B,再根据等腰三角形的性质和三角形的内角定理判断C、D.
【详解】解:根据图中尺规作图可知,AC的垂直平分线交AB于D,BP平分∠ABC,
∴,;选项A、B正确;
∵,
∴∠ACD=∠A =40°,
∵,,
∴∠ABC=∠ACB =70°,
∴,选项D错误;
∴∠BPC=180°-∠CBP-∠BCP =115°,选项C正确;
故选:D
【点拨】本题考查了基本作图,垂直平分线的性质,角平分线的定义,等腰三角形的性质,熟练掌握相关的知识是解题的关键
7.C
【分析】由的垂直平分线交于点D,交于点E,易得,又由的周长是,可求得,继而求得答案.
【详解】解:∵是的垂直平分线,
∴,
∵的周长是,
∴,
∵,
∴的周长是:.
故选:C.
【点拨】此题考查了线段垂直平分线的性质.此题难度不大,注意转化思想与数形结合思想的应用.
8.C
【详解】此题主要考查学生的动手实践能力和想象能力
由平面图形的折叠的特点结合实际操作解题.
通过自己动手,亲自实践一下,很容易得出正确结果为C.故选C.
9.A
【分析】本题考查了轴对称的性质:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.根据轴对称的性质可求、的长度,然后根据线段的和差求解即可.
【详解】解:∵点关于的对称点恰好落在线段上,,
∴,
同理,
又∵,
∴.
故选:A.
10.B
【分析】本题考查了全等三角形的判定和性质,角平分线的性质,添加恰当辅助线构造全等三角形是解题的关键.
【详解】解:如图,在上截取,连接,
平分,平分,
,,
,
,
,
,
,
在和中,
,
,
,
,
在和中,
,
,
,
,
周长为20,
,
,
,
.
故选:B.
11.角平分线所在的直线
【分析】根据角平分线的定义即可解答.
【详解】解:角的对称轴是“角平分线所在的直线”.
故答案为:角平分线所在的直线.
【点拨】本题主要考查了轴对称图形,理解轴对称图形沿对称轴折叠能够完全重合是解题的关键.
12.11
【分析】本题主要考查了轴对称的性质.根据轴对称的性质可得,,进而得出,再根据三角形的周长公式,即可求解.
【详解】解:∵点A与点E关于直线对称,
∴,,
∵,
∴,
∴的周长.
故答案为:11.
13./100度
【分析】本题主要考查了正方形的性质以及折叠的性质,由正方形的性质得出,由平行的性质得出,由叠的性质可知:,再由平角的定义即可求出.
【详解】解:∵是正方形,
∴,
∴,
由折叠的性质可知:,
∴,
故答案为:.
14.50
【分析】本题主要考查最短路径问题、轴对称的性质,三角形外角的性质,作M关于的对称点,N关于的对称点,连接,交于点P,交于点Q,连接,,可知此时最小,此时,,再根据三角形外角的性质和平角的定义即可得出结论.
【详解】解:作M关于的对称点,N关于的对称点,连接,交于点P,交于点Q,连接,,如图所示.
根据两点之间,线段最短,可知此时最小,即,
∴,,
∵,,
∴,,
∵,,
∴,
∴,
故答案为:50.
15.10
【分析】本题考查了轴对称最短路线问题的应用,垂直平分线的性质,准确找出点D的位置是解答本题的关键.根据垂直平分线的性质可知,点B与点C关于对称,故当点D与点P重合时,的值最小,最小值等于的长,由此即可得到答案.
【详解】垂直平分,
点B与点C关于对称,
如图,设与相较于点P,
当点D与点P重合时,的值最小,最小值等于的长,
,,
周长的最小值是,
故答案为:10.
16.
【分析】过D作DF⊥BC于F,依据角平分线的性质,即可得到AD=FD,再根据S△BCD=26,即可得出DF的长,进而得到AD的长.
【详解】如图,过D作DF⊥BC于F,
∵∠A=90°,CD平分∠ACB,
∴AD=FD,
∵S△BCD=26,BC=13,
∴×13×DF=26,
∴DF=4,AD=4.
故答案为:4.
【点拨】本题主要考查了角平分线的性质以及平行线的判定,角的平分线上的点到角的两边的距离相等.
17.3.5
【分析】根据等腰三角形的性质计算即可;
【详解】设等腰三角形的一条腰为x,
∵腰三角形的周长为12,底边长为5,
∴,
解得;
故答案是3.5.
【点拨】本题主要考查了等腰三角形的性质,准确分析计算是解题的关键.
18.120°
【分析】此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.根据要使的周长最小,即利用点的对称,让三角形的三边在同一直线上,A关于和的对称点,,即可得出,进而得出即可得出答案.
【详解】解:作关于和的对称点,,连接,,交于M,交于N,则即为的周长最小值.作延长线,
∵,
∴,
∴,
∵,,
且,,
∴,
故答案为:.
19.
【分析】本题考查了对称的性质、三角形的外角定理等知识,根据对称有,,从而,,可先求出的度数,然后根据外角,进而求出的度数,从而求解.
【详解】解:∵和关于直线对称,
∴,,
∴,.
∵,
∴.
又∵
∴
∴
20.(1)见解析;(2)3:2:4
【分析】(1)依据题干要求作出图形即可;
(2)根据角平分线的性质可得△ABO中AB边上的高和△ACO中AC边上的高以及△BCO中BC边上的高相等,从而得到的比值等于AB:AC:BC.
【详解】解:(1)如图,即为所作图形;
(2)∵AO平分∠BAC,BE平分∠ABC,
∴OC平分∠ACB,
∴点O到AB、BC和AC的距离相等,
即△ABO中AB边上的高和△ACO中AC边上的高以及△BCO中BC边上的高相等,
∵AB=6,BC=4,AC=8,
∴=AB:AC:BC=6:4:8=3:2:4.
【点拨】本题考查了尺规作图,角平分线的性质,解题的关键是根据角平分线的性质得到三角形的高相等.
21.(1)∠A的度数30°;
(2)∠CBD的度数为45°
【分析】(1)根据等腰三角形的性质、三角形内角和定理即可求出∠A的度数;
(2)根据线段垂直平分线的性质得到DA=DB,得到∠DBA=∠A,再计算即可.
【详解】(1)解:∵AB=AC,∠C=75°,
∴∠ABC=∠C=75°,
∴∠A=180°-75°-75°=30°,
∴∠A的度数30°;
(2)解:∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DBA=∠A=30°,
∴∠CBD=∠ABC-∠ABD=75°-30°=45°,
∴∠CBD的度数为45°.
【点拨】本题考查了线段垂直平分线、等腰三角形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
22.4
【分析】连接AP,根据和AB=AC,即可得.
【详解】解:如图所示,连接AP,
∴,
∵AB=AC,
∴,
∵,
∴,
∴,
【点拨】本题考查了等腰三角形的性质,解题的关键是知道三角形ABC,三角形ABP,三角形ACP面积之间的关系.
23.(1),
(2)
【分析】本题主要考查了轴对称的性质,解题的关键是熟练掌握性质,准确计算.
(1)本题考查轴对称的性质,根据轴对称的性质解答即可.
(2)本题根据轴对称性质推出,从而得出,最后根据即可解题.
【详解】(1)解:由题意可得:图中点的对应点是点,的对应边是,
故答案为:,.
(2)解:,
,
,
.
24.(1)依据1:角平分线上的点到角的两边的距离相等;依据2:等量代换;依据3:角的内部到角的两边距离相等的点在这个角的平分线上;(2)或.
【分析】(1)根据题意可直接进行作答;
(2)由(1)可得OD=OE=OF,然后根据等积法进行求解即可.
【详解】解:(1)由题意得:
依据1:角平分线上的点到角的两边的距离相等.
依据2:等量代换.
依据3:角的内部到角的两边距离相等的点在这个角的平分线上.
(2)由(1)得:
OD=OE=OF=r,
,,,
,
△ABC的面积表示为:.
【点拨】本题主要考查角平分线的性质定理及判定定理,熟练掌握角平分线的性质定理及判定定理是解题的关键.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
