人教版数学九年级下册28.2.2 第2课时 与方向角,坡角有关的实际应用 教案
文档属性
| 名称 | 人教版数学九年级下册28.2.2 第2课时 与方向角,坡角有关的实际应用 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 52.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 19:22:02 | ||
图片预览

文档简介
第二十八章 锐角三角函数
28.2.2应用举例
第二课时:与方向角,坡角有关的实际应用
一、教学目标
1.了解方向角的概念,并熟练运用解直角三角形的知识解决与方向角有关的实际问题。
2.理解坡角,坡度等概念,进一步培养应用数学模型思想解决实际问题的能力。
二、教学重难点
重点:了解方向角的概念,并熟练运用解直角三角形的知识解决与方向角有关的实际问题。
难点:理解坡角,坡度等概念,进一步培养应用数学模型思想解决实际问题的能力。
三、教学过程
【新课导入】
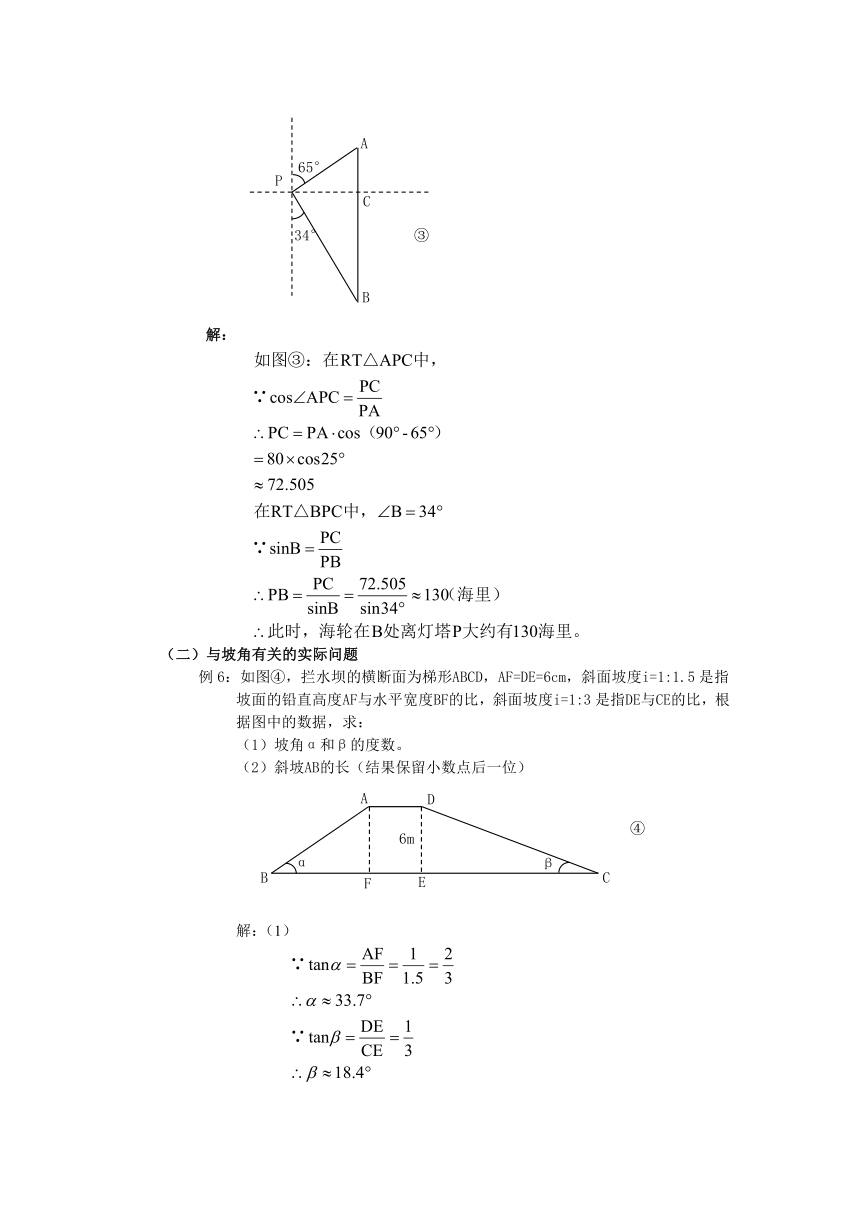
复习方向角:
方向角:指正北或指正南方向线与目标方向线所成的小于90°的角.
(
60°
30°
80°
45°
A
东
B
南
C
北
D
西
O
)如果①,目标方向线OA,OB,OC,OD的方向角分别表示为北偏东30°,南偏东45°(东南方向),南偏西80°,北偏西60°.
(
α
h
②
l
)
(二)认识坡角,坡度
坡度:通常把坡面的垂直高度h和水平宽度l的比叫做坡度(或坡比),
字母i表示,即
坡角:坡角α是坡面与水平面的夹角。
【新知探究】
与方向角有关的实际问题
例5:如图③,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,B处距离灯塔P有多远(结果取整数)。
(
P
A
B
C
34°
65°
③
)
解:
与坡角有关的实际问题
例6:如图④,拦水坝的横断面为梯形ABCD,AF=DE=6cm,斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比,斜面坡度i=1:3是指DE与CE的比,根据图中的数据,求:
坡角α和β的度数。
斜坡AB的长(结果保留小数点后一位)
(
A
B
D
α
F
E
β
C
6m
④
)
解:(1)
(2)
归纳:
利用解直角三角形的知识解决实际问题的一般过程是:
将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题)。
根据问题中的条件,适当选用锐角三角函数等解直角三角形。
得到数学问题的答案。
得到实际问题的答案
【课堂小结】
(一)方向角:
方向角:指正北或指正南方向线与目标方向线所成的小于90°的角.
(二)坡角与坡度:
坡度:通常把坡面的垂直高度h和水平宽度l的比叫做坡度(或坡比),用字母i表示,即
坡角:坡角α是坡面与水平面的夹角。
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题)。
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形。
(3)得到数学问题的答案。
(4)得到实际问题的答案.
【课堂训练】
1.如图⑤,某水库堤坝横断面迎水坡AB的坡比是,堤坝高BC=50 m,则迎水坡面AB的长度是(C)
(
P
A
B
⑥
) A. B. C.100 m D.150 m
(
B
A
C
⑤
)
2.如图⑥,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为(A)
A. B. C.80海里 D.
3.小明沿着坡度为1∶2的山坡向上走了1000m,则他升高了( A )
A. B. 500 C. D. 1000
(
B
45°
60°
A
C
⑦
北
) 4.科技改变生活,手机导航极大方便了人们的出行,如图⑦,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4km到B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地正北方向,求B,C两地的距离.
(
D
)
解:
5.如图⑧,拦水坝的横断面为梯形ABCD,已知上底长CB=5m,迎水面坡度为,背水面坡度为1∶1,坝高为4m,求:
(1)坝底AD的长.
(2)迎水坡CD的长.
(
C
B
D
α
F
E
β
A
⑧
) (3)坡角α,β的度数.
解:
28.2.2应用举例
第二课时:与方向角,坡角有关的实际应用
一、教学目标
1.了解方向角的概念,并熟练运用解直角三角形的知识解决与方向角有关的实际问题。
2.理解坡角,坡度等概念,进一步培养应用数学模型思想解决实际问题的能力。
二、教学重难点
重点:了解方向角的概念,并熟练运用解直角三角形的知识解决与方向角有关的实际问题。
难点:理解坡角,坡度等概念,进一步培养应用数学模型思想解决实际问题的能力。
三、教学过程
【新课导入】
复习方向角:
方向角:指正北或指正南方向线与目标方向线所成的小于90°的角.
(
60°
30°
80°
45°
A
东
B
南
C
北
D
西
O
)如果①,目标方向线OA,OB,OC,OD的方向角分别表示为北偏东30°,南偏东45°(东南方向),南偏西80°,北偏西60°.
(
α
h
②
l
)
(二)认识坡角,坡度
坡度:通常把坡面的垂直高度h和水平宽度l的比叫做坡度(或坡比),
字母i表示,即
坡角:坡角α是坡面与水平面的夹角。
【新知探究】
与方向角有关的实际问题
例5:如图③,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,B处距离灯塔P有多远(结果取整数)。
(
P
A
B
C
34°
65°
③
)
解:
与坡角有关的实际问题
例6:如图④,拦水坝的横断面为梯形ABCD,AF=DE=6cm,斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比,斜面坡度i=1:3是指DE与CE的比,根据图中的数据,求:
坡角α和β的度数。
斜坡AB的长(结果保留小数点后一位)
(
A
B
D
α
F
E
β
C
6m
④
)
解:(1)
(2)
归纳:
利用解直角三角形的知识解决实际问题的一般过程是:
将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题)。
根据问题中的条件,适当选用锐角三角函数等解直角三角形。
得到数学问题的答案。
得到实际问题的答案
【课堂小结】
(一)方向角:
方向角:指正北或指正南方向线与目标方向线所成的小于90°的角.
(二)坡角与坡度:
坡度:通常把坡面的垂直高度h和水平宽度l的比叫做坡度(或坡比),用字母i表示,即
坡角:坡角α是坡面与水平面的夹角。
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题)。
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形。
(3)得到数学问题的答案。
(4)得到实际问题的答案.
【课堂训练】
1.如图⑤,某水库堤坝横断面迎水坡AB的坡比是,堤坝高BC=50 m,则迎水坡面AB的长度是(C)
(
P
A
B
⑥
) A. B. C.100 m D.150 m
(
B
A
C
⑤
)
2.如图⑥,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为(A)
A. B. C.80海里 D.
3.小明沿着坡度为1∶2的山坡向上走了1000m,则他升高了( A )
A. B. 500 C. D. 1000
(
B
45°
60°
A
C
⑦
北
) 4.科技改变生活,手机导航极大方便了人们的出行,如图⑦,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4km到B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地正北方向,求B,C两地的距离.
(
D
)
解:
5.如图⑧,拦水坝的横断面为梯形ABCD,已知上底长CB=5m,迎水面坡度为,背水面坡度为1∶1,坝高为4m,求:
(1)坝底AD的长.
(2)迎水坡CD的长.
(
C
B
D
α
F
E
β
A
⑧
) (3)坡角α,β的度数.
解:
