第11章 反比例函数单元检测卷(含答案)
文档属性
| 名称 | 第11章 反比例函数单元检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 739.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
江苏省南京市外国语学校第11章反比例函数检测卷-2023-2024学年数学八年级下册苏科版
注意事项:
1.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上,答在本试卷上无效.
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.下列各问题情境中都包含一对变量,其中属于反比例函数关系的是( )
A.直角三角形中两锐角之间的关系.
B.匀速行驶的汽车经过的路程与时间的关系.
C.正方形的面积与边长的关系.
D.电压不变的电路中,电流强度与电阻的关系.
2.若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )
A. B.
C. D.
3.已知反比例函数y=﹣ ,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则﹣2<y<0
4. 如果反比例函数 是常数)的图像在第二、四象限,那么a的取值范围是 ( )
A.a<0 B.a>0 C. D.
5.如图,P 是第二象限内的反比例函数图象上的一点,若矩形 PEOF 的面积为 3,则反比例函数的表达式为 ( )
A. B. C. D.
6.若反比例函数 的图像经过点(2,-3),则它的图像也一定经过点 ( )
A.(-2,-3) B.(-2,3) C.(3,2) D.(-3,-2)
二、填空题(本大题共10小题,每小题2分,共20分.请把答案填写在答题卡相应位置上)
7.已知 是反比例函数,那么k的值是 .
8.已知反比例函数 的图像位于第二、四象限,则k的取值范围是 .
9.已知反比例函数,这个函数的自变量的取值范围是 当时,函数的值是 ;当时,自变量的值是 .
10.在平面直角坐标系 xOy中,直线y=x与反比例函数的图像相交于 A,B 两点.若点 A,B的纵坐标分别为 y ,y ,则 y +y 的值为 .
11.点A 在第二象限,且在反比例函数的图象上,则点 A 的坐标可以是 .(只需写出一个符合条件的坐标)
12.如图,在平面直角坐标系中,矩形ABCD的边BC⊥y轴,反比例函数的图象经过点C,且与AD边相交于点E,连结CE.若CE=5,BC=6,AE=2,则k的值为 。
13.若正比例函数 y=kx(k≠0)与反比例函数 y= 的图象相交于A(x ,y ),B(x ,y )两点,则代数式 的值为 .
14.如图,在平面直角坐标系中,一次函数y=-4x+4 的图象与 x轴、y轴分别相交于点A,B.正方形ABCD 的顶点C,D位于第一象限,其中顶点 D 位于反比例函.数 的图象上.若将正方形ABCD 向左平移n个单位后,顶点C恰好落在该反比例函数的图象上,则 n的值是 .
.
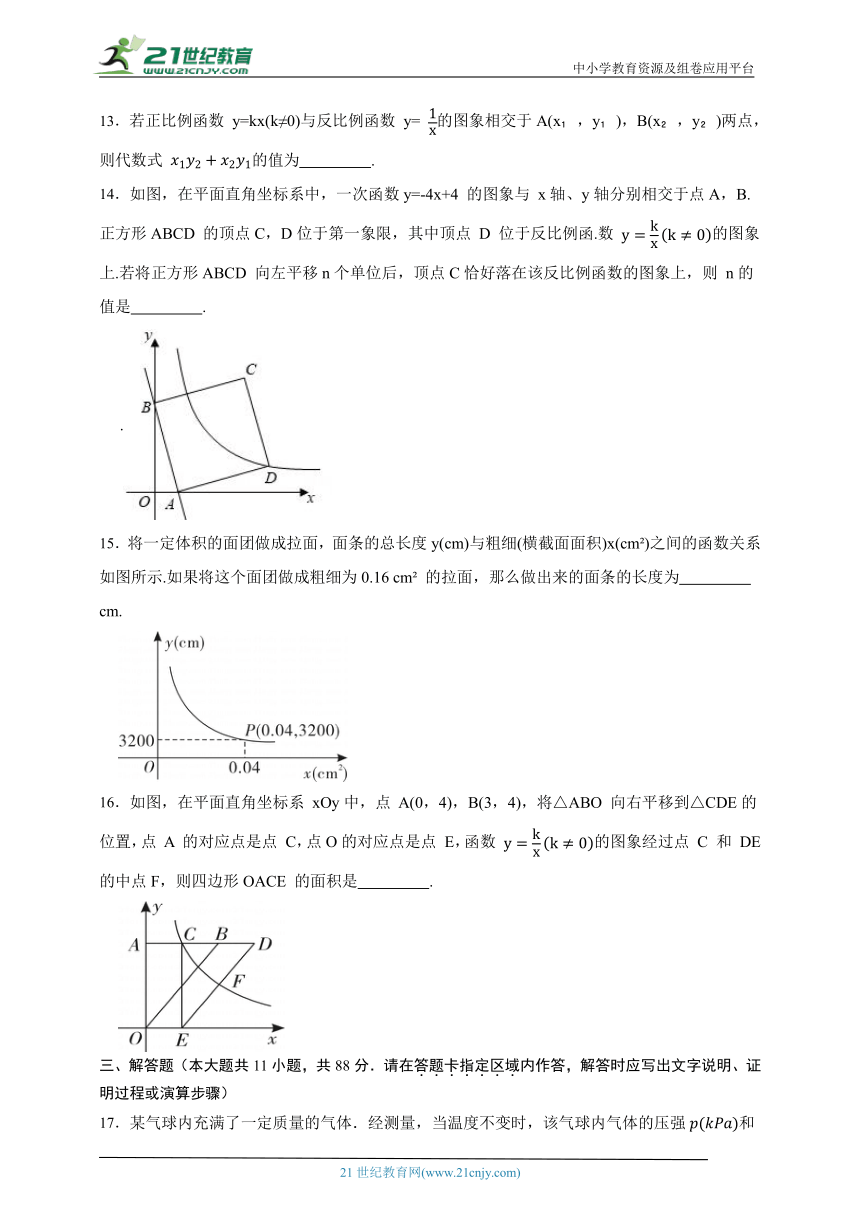
15.将一定体积的面团做成拉面,面条的总长度y(cm)与粗细(横截面面积)x(cm )之间的函数关系如图所示.如果将这个面团做成粗细为0.16 cm 的拉面,那么做出来的面条的长度为 cm.
16.如图,在平面直角坐标系 xOy中,点 A(0,4),B(3,4),将△ABO 向右平移到△CDE的位置,点 A 的对应点是点 C,点O的对应点是点 E,函数 的图象经过点 C 和 DE的中点F,则四边形OACE 的面积是 .
三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17.某气球内充满了一定质量的气体.经测量,当温度不变时,该气球内气体的压强和气体体积的几组对应值如下表:
0.8 1 1.2 1.4 1.6
119 95 79 68 59
(1)根据表中的数据画出函数图象,并求出压强关于体积的函数表达式.
(2)当气体体积为时,气球内气体的压强是多少(精确到)?
(3)当气球内气体的压强大于时,气球将爆炸.为了安全起见,气球的体积应不小于多少(精确到)?
18.要制作一种糖质工艺品,需先把材料加热到才能进行操作.设材料的温度为,从加热开始计算的时间为.该材料在加热时,温度与时间的函数关系图象是一次函数图象的一部分;停止加热后,温度与时间的函数关系图象是反比例函数图象的一部分.已知该材料加热前的温度是,加热时温度达到.
(1)分别求出材料加热过程中及停止加热后,关于的函数表达式.
(2)为节约能源,加工时采用间歇加热法,即把材料加热到后停止加热,等温度降至时,再次加热到后停止加热.那么从第一次加热至可以操作到第二次再需加热,整个过程可操作的时间有多长?
19.如图,的面积为长为上的高DE长为.
(1)写出关于的函数表达式及自变量的取值范围.
(2)若,对角线,求的周长.
20.设面积为的平行四边形的一边长为,这条边上的高线长为.
(1)求关于的函数表达式和自变量的取值范围.
(2)当边长时,求这条边上的高线长.
21.已知x,y满足下表:
… -4 -2 -1 1 2 4 …
… -1 -2 -4 4 2 1 …
(1)求关于的函数表达式.
(2)求当自变量的值是10时函数的值.
(3)若当自变量是-6时,函数值是2m,求的值.
22.已知小聪家与学校相距3000米,他从家里出发骑自行车去学校,设速度为(米/分),到达学校所用的时间为(分).
(1)求关于的函数表达式.这个函数是反比例函数吗?如果是,说出比例系数.
(2)求当时自变量的值,并说明这个值的实际意义.
(3)利用关于的函数表达式说明:若小聪到达学校所用的时间减少到原来的,则他骑车的速度应怎样变化?
23.如图,已知一次函数的图象与反比例函数:的图象相交于点A(1,2)和点B.
(1)求b和k的值.
(2)请求出点B的坐标,并观察图象,直接写出关于x(x<0)的不等式的解.
24.如图,反比例函数与一次函数的图象相交于A,B两点,AE⊥x轴,直线与x轴、y轴分别相交于C,D两点,
(1)求反比例函数与一次函数的表达式.
(2)当y2>y1时,求x的取值范围.
(3)在反比例函数的图象上(除点B外)还存在到点O的距离等于线段OA长的点吗 若不存在,请说明理由;若存在,直接写出该点的坐标.
25.如图,OA=OB,∠AOB=90°,点A(1,4),B分别在反比例函数x>0)x>0)和 的图像上.
(1)求 k ,k 的值.
(2)若点 C,D分别在反比例函数 0)和的图像上,且不与点 A,B 重合,则是否存在点 C,D,使得△COD≌△AOB 若存在,请直接写出点 C,D的坐标;若不存在,请说明理由.
26.如图,一次函数y=x+1的图像与反比例函数 的图象相交,其中一个交点的横坐标是 2.
(1)求反比例函数的表达式。
(2)将一次函数y=x+1的图象向下平移2个单位,求平移后的图像象与反比例函数图象的交点坐标。
(3)直接写出一个一次函数,使其图像经过点(0,5),且与反比例函数 的图象没有公共点。
27.已知直线y=x与反比例函数 的图象在第一象限相交于点 M(2,a).
(1)求反比例函数的表达式.
(2)如图,将直线y=x向上平移b个单位后与的图像相交于点A(1,m)和点 B(n,-1),求b的值.
(3)在(2)的条件下,设直线 AB 与x轴、y轴分别相交于点C,D,求证:△AOD≌△BOC.
答案解析部分
1.D
2.B
3.B
4.C
5.A
6.B
7.-2
8.
9.x≠0;;x=-1
10.0
11.(-3,4)(答案不唯一)
12.9
13.-2
14.3
15.800
16.6
17.(1)解:如图
设函数解析式为,
把(1,95)代入,得:k=95
∴函数解析式为;
(2)解:当时,;
(3)解:当时,
∴ 为了安全起见,气球的体积应不小于.
18.(1)解:加热过程中与时间的函数关系图象是一次函数 ,
设y=kx+b(0≤x≤5)
把(0,30),(5,100)代入得
,解得,
∴函数解析式为y=14x+30;
停止加热后,图象是反比例函数,
设解析式为
把(5,100)代入,可得a=500
∴函数解析式为
综上所述:
(2)解:由(1)得,当y=40时,14x+30=40,解得:
,解得x=12.5,
分钟
从第一次加热至可以操作到第二次再需加热,整个过程操作的时间分钟.
19.(1)解:的面积为,
∴;
(2)解:由题意得:x=4时,,即,
在Rt△BDE中,由勾股定理得:,
∴CE=BE-BC=6-4=2,
在Rt△CDE中,由勾股定理得:,
∴的周长.
20.(1)解:由题意得:ah=12,
∴;
(2)解:把代入,得h=2
当边长时, 这条边上的高线长2cm.
21.(1)解:由表格数据可知:xy=4
∴;
(2)解:当x=10时,;
(3)解:把x=-6,y=2m代入,得,
解得:
22.(1)解:由题意得:,是反比例函数,比例系数为3000;
(2)解:把代入,得,
解得:t=15
实际意义:当速度为 200米/分时,到达学校所用的时间为15分钟
(3)解: ∵小聪到达学校所用的时间减少到原来的,
∴,
即他骑车的速度应变为原来的倍.
23.(1)解:∵一次函数与反比例函数的图象相交于点A(-1,2),
∴2=×(-1)+b,2=,
解得:b=,k=-2;
(2)解:点
24.(1)解:由题意得:,
∴
反比例函数图象位于二、四象限,
∴
故反比例函数的表达式为,
∵AE⊥x轴,,
∴∠ACE=45°,
∴∠OCD=∠ACE=45°,
∴OC=OD,
∴
故一次函数的表达式为;
(2)解:,
得或,
∴A(-2,1),B(1,-2),
由图象可得:时,x<2或0(3)解:存在, 反比例函数图象上到点O的距离等于线段OA长的点 ,这两点与A、B关于y=-x对称,
故该点的坐标为(1,2)和(2,1).
25.(1)解:过点A作AG⊥y轴于G,过点B作BH⊥y轴于H,如图:
∵A(1,4)在反比例函数上,
将(1,4)代入得:,解得:;
则AG=1,OG=4;
∵∠AOB=∠AOG+∠BOH=∠BOH+∠OBH=90°,
∴∠AOG=∠OBH,
∵OA=OB,∠AGO=∠BHO=90°,
∴△AGO≌△OHB(AAS),
∴OH=AG=1,BH=OG=4,
∴B(4,-1),
∵B(4,-1)在反比例函数上,
将(4,-1)代入得:,解得:.
(2)解:存在,理由如下:
如图,
∵△COD≌△AOB,
∴OA=OB=OC=OD,
∴B与C关于x轴对称,A与D关于x轴对称,
∴C(4,1),D(1,-4).
26.(1)解:将x=2代入y=x+1得y=3,
∴ 一次函数y=x+1的图象与反比例函数 的图象的一个交点坐标为(2,3);
将点(2,3)代入得k=6,
∴反比例函数的表达式为: ;
(2)解:∵将一次函数y=x+1的图象向下平移2个单位,
∴平移后的函数解析式为y=x-1,
解,得和,
∴平移后一次函数的图象与反比例函数图象的交点坐标为:(-2,-3)和(3,2);
(3)y=-2x+5(答案不唯一)
27.(1)解:将点M(2,a)代入y=x得a=2,
∴M(2,2),
∵点M在反比例函数 得图象上,
∴k=4,
∴ 反比例函数的表达式为:y= ;
(2)解: ∵点A(1,m)和点B(n,-1)都在反比例函数得图象上,
∴m=4,n=-4,
∴ 点A(1,4)、点 B(-4,-1) ,
∵ 将直线y=x向上平移b个单位,
∴平移后的函数解析式为y=x+b,
将点A(1,4)代入y=x+b得b=3;
(3)证明:由(2)易得直线AB的解析式为y=x+3,
令y=x+3中的x=0,得y=3,
∴点D(0,3);
令y=x+3中的y=0,得x=-3,
∴C(-3,0),
又A(1,4)、B(-4,-1) 、O(0,0),
∴AO=BO=,CO=DO=3,AD=,BC=,
∴AD=BC,
∴△AOD≌△BOC(SSS).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
江苏省南京市外国语学校第11章反比例函数检测卷-2023-2024学年数学八年级下册苏科版
注意事项:
1.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上,答在本试卷上无效.
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.下列各问题情境中都包含一对变量,其中属于反比例函数关系的是( )
A.直角三角形中两锐角之间的关系.
B.匀速行驶的汽车经过的路程与时间的关系.
C.正方形的面积与边长的关系.
D.电压不变的电路中,电流强度与电阻的关系.
2.若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )
A. B.
C. D.
3.已知反比例函数y=﹣ ,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则﹣2<y<0
4. 如果反比例函数 是常数)的图像在第二、四象限,那么a的取值范围是 ( )
A.a<0 B.a>0 C. D.
5.如图,P 是第二象限内的反比例函数图象上的一点,若矩形 PEOF 的面积为 3,则反比例函数的表达式为 ( )
A. B. C. D.
6.若反比例函数 的图像经过点(2,-3),则它的图像也一定经过点 ( )
A.(-2,-3) B.(-2,3) C.(3,2) D.(-3,-2)
二、填空题(本大题共10小题,每小题2分,共20分.请把答案填写在答题卡相应位置上)
7.已知 是反比例函数,那么k的值是 .
8.已知反比例函数 的图像位于第二、四象限,则k的取值范围是 .
9.已知反比例函数,这个函数的自变量的取值范围是 当时,函数的值是 ;当时,自变量的值是 .
10.在平面直角坐标系 xOy中,直线y=x与反比例函数的图像相交于 A,B 两点.若点 A,B的纵坐标分别为 y ,y ,则 y +y 的值为 .
11.点A 在第二象限,且在反比例函数的图象上,则点 A 的坐标可以是 .(只需写出一个符合条件的坐标)
12.如图,在平面直角坐标系中,矩形ABCD的边BC⊥y轴,反比例函数的图象经过点C,且与AD边相交于点E,连结CE.若CE=5,BC=6,AE=2,则k的值为 。
13.若正比例函数 y=kx(k≠0)与反比例函数 y= 的图象相交于A(x ,y ),B(x ,y )两点,则代数式 的值为 .
14.如图,在平面直角坐标系中,一次函数y=-4x+4 的图象与 x轴、y轴分别相交于点A,B.正方形ABCD 的顶点C,D位于第一象限,其中顶点 D 位于反比例函.数 的图象上.若将正方形ABCD 向左平移n个单位后,顶点C恰好落在该反比例函数的图象上,则 n的值是 .
.
15.将一定体积的面团做成拉面,面条的总长度y(cm)与粗细(横截面面积)x(cm )之间的函数关系如图所示.如果将这个面团做成粗细为0.16 cm 的拉面,那么做出来的面条的长度为 cm.
16.如图,在平面直角坐标系 xOy中,点 A(0,4),B(3,4),将△ABO 向右平移到△CDE的位置,点 A 的对应点是点 C,点O的对应点是点 E,函数 的图象经过点 C 和 DE的中点F,则四边形OACE 的面积是 .
三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17.某气球内充满了一定质量的气体.经测量,当温度不变时,该气球内气体的压强和气体体积的几组对应值如下表:
0.8 1 1.2 1.4 1.6
119 95 79 68 59
(1)根据表中的数据画出函数图象,并求出压强关于体积的函数表达式.
(2)当气体体积为时,气球内气体的压强是多少(精确到)?
(3)当气球内气体的压强大于时,气球将爆炸.为了安全起见,气球的体积应不小于多少(精确到)?
18.要制作一种糖质工艺品,需先把材料加热到才能进行操作.设材料的温度为,从加热开始计算的时间为.该材料在加热时,温度与时间的函数关系图象是一次函数图象的一部分;停止加热后,温度与时间的函数关系图象是反比例函数图象的一部分.已知该材料加热前的温度是,加热时温度达到.
(1)分别求出材料加热过程中及停止加热后,关于的函数表达式.
(2)为节约能源,加工时采用间歇加热法,即把材料加热到后停止加热,等温度降至时,再次加热到后停止加热.那么从第一次加热至可以操作到第二次再需加热,整个过程可操作的时间有多长?
19.如图,的面积为长为上的高DE长为.
(1)写出关于的函数表达式及自变量的取值范围.
(2)若,对角线,求的周长.
20.设面积为的平行四边形的一边长为,这条边上的高线长为.
(1)求关于的函数表达式和自变量的取值范围.
(2)当边长时,求这条边上的高线长.
21.已知x,y满足下表:
… -4 -2 -1 1 2 4 …
… -1 -2 -4 4 2 1 …
(1)求关于的函数表达式.
(2)求当自变量的值是10时函数的值.
(3)若当自变量是-6时,函数值是2m,求的值.
22.已知小聪家与学校相距3000米,他从家里出发骑自行车去学校,设速度为(米/分),到达学校所用的时间为(分).
(1)求关于的函数表达式.这个函数是反比例函数吗?如果是,说出比例系数.
(2)求当时自变量的值,并说明这个值的实际意义.
(3)利用关于的函数表达式说明:若小聪到达学校所用的时间减少到原来的,则他骑车的速度应怎样变化?
23.如图,已知一次函数的图象与反比例函数:的图象相交于点A(1,2)和点B.
(1)求b和k的值.
(2)请求出点B的坐标,并观察图象,直接写出关于x(x<0)的不等式的解.
24.如图,反比例函数与一次函数的图象相交于A,B两点,AE⊥x轴,直线与x轴、y轴分别相交于C,D两点,
(1)求反比例函数与一次函数的表达式.
(2)当y2>y1时,求x的取值范围.
(3)在反比例函数的图象上(除点B外)还存在到点O的距离等于线段OA长的点吗 若不存在,请说明理由;若存在,直接写出该点的坐标.
25.如图,OA=OB,∠AOB=90°,点A(1,4),B分别在反比例函数x>0)x>0)和 的图像上.
(1)求 k ,k 的值.
(2)若点 C,D分别在反比例函数 0)和的图像上,且不与点 A,B 重合,则是否存在点 C,D,使得△COD≌△AOB 若存在,请直接写出点 C,D的坐标;若不存在,请说明理由.
26.如图,一次函数y=x+1的图像与反比例函数 的图象相交,其中一个交点的横坐标是 2.
(1)求反比例函数的表达式。
(2)将一次函数y=x+1的图象向下平移2个单位,求平移后的图像象与反比例函数图象的交点坐标。
(3)直接写出一个一次函数,使其图像经过点(0,5),且与反比例函数 的图象没有公共点。
27.已知直线y=x与反比例函数 的图象在第一象限相交于点 M(2,a).
(1)求反比例函数的表达式.
(2)如图,将直线y=x向上平移b个单位后与的图像相交于点A(1,m)和点 B(n,-1),求b的值.
(3)在(2)的条件下,设直线 AB 与x轴、y轴分别相交于点C,D,求证:△AOD≌△BOC.
答案解析部分
1.D
2.B
3.B
4.C
5.A
6.B
7.-2
8.
9.x≠0;;x=-1
10.0
11.(-3,4)(答案不唯一)
12.9
13.-2
14.3
15.800
16.6
17.(1)解:如图
设函数解析式为,
把(1,95)代入,得:k=95
∴函数解析式为;
(2)解:当时,;
(3)解:当时,
∴ 为了安全起见,气球的体积应不小于.
18.(1)解:加热过程中与时间的函数关系图象是一次函数 ,
设y=kx+b(0≤x≤5)
把(0,30),(5,100)代入得
,解得,
∴函数解析式为y=14x+30;
停止加热后,图象是反比例函数,
设解析式为
把(5,100)代入,可得a=500
∴函数解析式为
综上所述:
(2)解:由(1)得,当y=40时,14x+30=40,解得:
,解得x=12.5,
分钟
从第一次加热至可以操作到第二次再需加热,整个过程操作的时间分钟.
19.(1)解:的面积为,
∴;
(2)解:由题意得:x=4时,,即,
在Rt△BDE中,由勾股定理得:,
∴CE=BE-BC=6-4=2,
在Rt△CDE中,由勾股定理得:,
∴的周长.
20.(1)解:由题意得:ah=12,
∴;
(2)解:把代入,得h=2
当边长时, 这条边上的高线长2cm.
21.(1)解:由表格数据可知:xy=4
∴;
(2)解:当x=10时,;
(3)解:把x=-6,y=2m代入,得,
解得:
22.(1)解:由题意得:,是反比例函数,比例系数为3000;
(2)解:把代入,得,
解得:t=15
实际意义:当速度为 200米/分时,到达学校所用的时间为15分钟
(3)解: ∵小聪到达学校所用的时间减少到原来的,
∴,
即他骑车的速度应变为原来的倍.
23.(1)解:∵一次函数与反比例函数的图象相交于点A(-1,2),
∴2=×(-1)+b,2=,
解得:b=,k=-2;
(2)解:点
24.(1)解:由题意得:,
∴
反比例函数图象位于二、四象限,
∴
故反比例函数的表达式为,
∵AE⊥x轴,,
∴∠ACE=45°,
∴∠OCD=∠ACE=45°,
∴OC=OD,
∴
故一次函数的表达式为;
(2)解:,
得或,
∴A(-2,1),B(1,-2),
由图象可得:时,x<2或0
故该点的坐标为(1,2)和(2,1).
25.(1)解:过点A作AG⊥y轴于G,过点B作BH⊥y轴于H,如图:
∵A(1,4)在反比例函数上,
将(1,4)代入得:,解得:;
则AG=1,OG=4;
∵∠AOB=∠AOG+∠BOH=∠BOH+∠OBH=90°,
∴∠AOG=∠OBH,
∵OA=OB,∠AGO=∠BHO=90°,
∴△AGO≌△OHB(AAS),
∴OH=AG=1,BH=OG=4,
∴B(4,-1),
∵B(4,-1)在反比例函数上,
将(4,-1)代入得:,解得:.
(2)解:存在,理由如下:
如图,
∵△COD≌△AOB,
∴OA=OB=OC=OD,
∴B与C关于x轴对称,A与D关于x轴对称,
∴C(4,1),D(1,-4).
26.(1)解:将x=2代入y=x+1得y=3,
∴ 一次函数y=x+1的图象与反比例函数 的图象的一个交点坐标为(2,3);
将点(2,3)代入得k=6,
∴反比例函数的表达式为: ;
(2)解:∵将一次函数y=x+1的图象向下平移2个单位,
∴平移后的函数解析式为y=x-1,
解,得和,
∴平移后一次函数的图象与反比例函数图象的交点坐标为:(-2,-3)和(3,2);
(3)y=-2x+5(答案不唯一)
27.(1)解:将点M(2,a)代入y=x得a=2,
∴M(2,2),
∵点M在反比例函数 得图象上,
∴k=4,
∴ 反比例函数的表达式为:y= ;
(2)解: ∵点A(1,m)和点B(n,-1)都在反比例函数得图象上,
∴m=4,n=-4,
∴ 点A(1,4)、点 B(-4,-1) ,
∵ 将直线y=x向上平移b个单位,
∴平移后的函数解析式为y=x+b,
将点A(1,4)代入y=x+b得b=3;
(3)证明:由(2)易得直线AB的解析式为y=x+3,
令y=x+3中的x=0,得y=3,
∴点D(0,3);
令y=x+3中的y=0,得x=-3,
∴C(-3,0),
又A(1,4)、B(-4,-1) 、O(0,0),
∴AO=BO=,CO=DO=3,AD=,BC=,
∴AD=BC,
∴△AOD≌△BOC(SSS).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
