18.1.1 平行四边形的性质 (1) 课件 (共16张PPT)人教版数学八年级下册
文档属性
| 名称 | 18.1.1 平行四边形的性质 (1) 课件 (共16张PPT)人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
18.1.1 平行四边形的性质(1)
人教版八年级下册
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
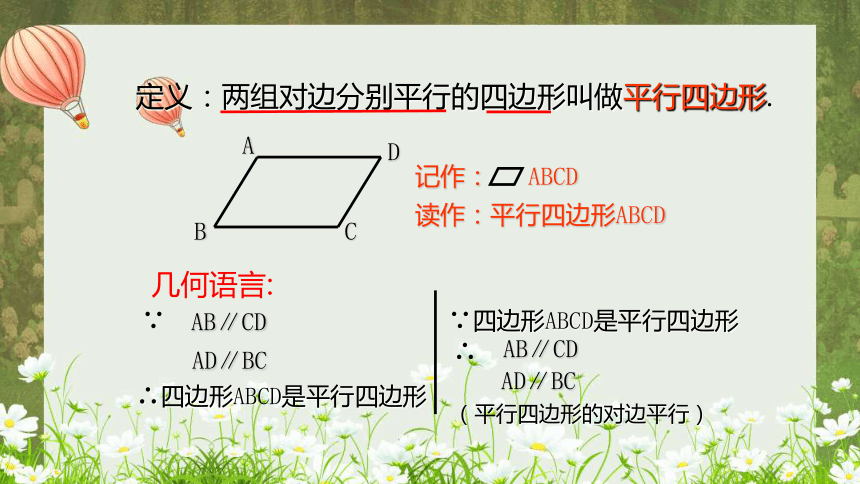
定义:两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
几何语言:
(平行四边形的对边平行)
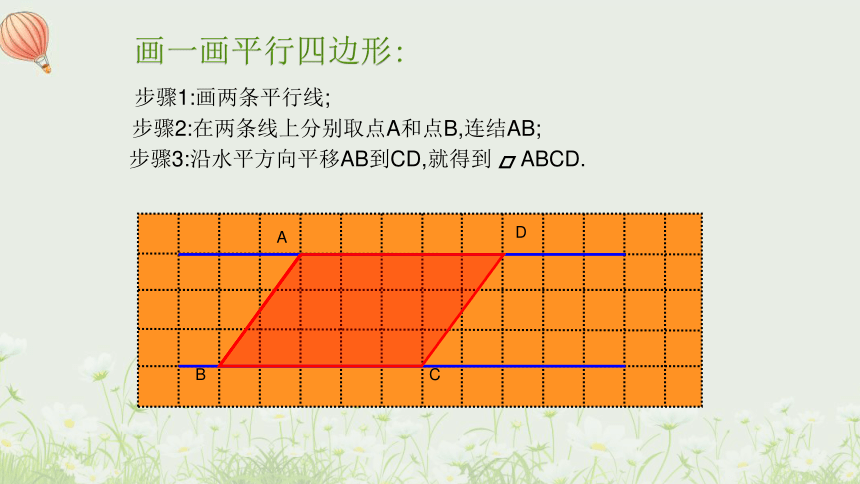
步骤3:沿水平方向平移AB到CD,就得到 ABCD.
A
B
C
D
步骤1:画两条平行线;
步骤2:在两条线上分别取点A和点B,连结AB;
画一画平行四边形:
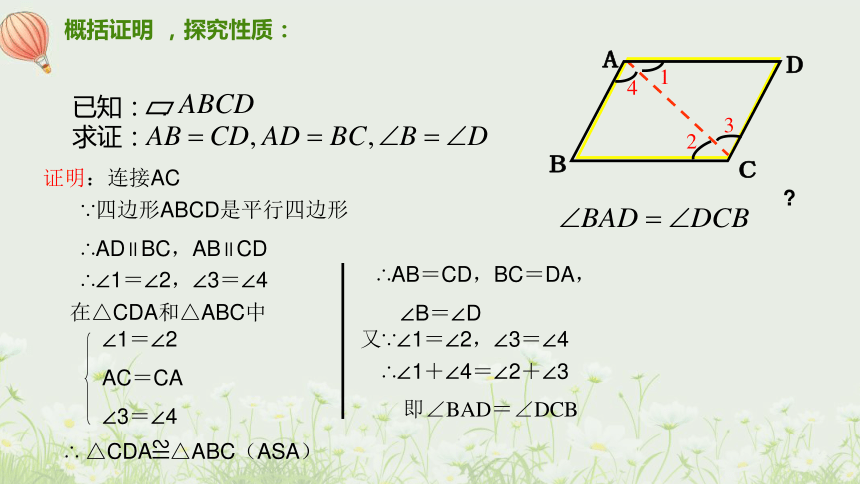
概括证明 ,探究性质:
活动:在几何图纸上任意画一个平行四边形,观察、测量、思考:
1:平行四边形对边有什么数量关系?
2:平行四边形对角有什么数量关系?
猜想:平行四边形对边相等,对角相等.
你能证明这些结论吗?
概括证明 ,探究性质:
已知: .
求证:
ABCD
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △CDA≌△ABC(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△CDA和△ABC中
证明:连接AC
A
B
C
D
C
O
B
D
A
o
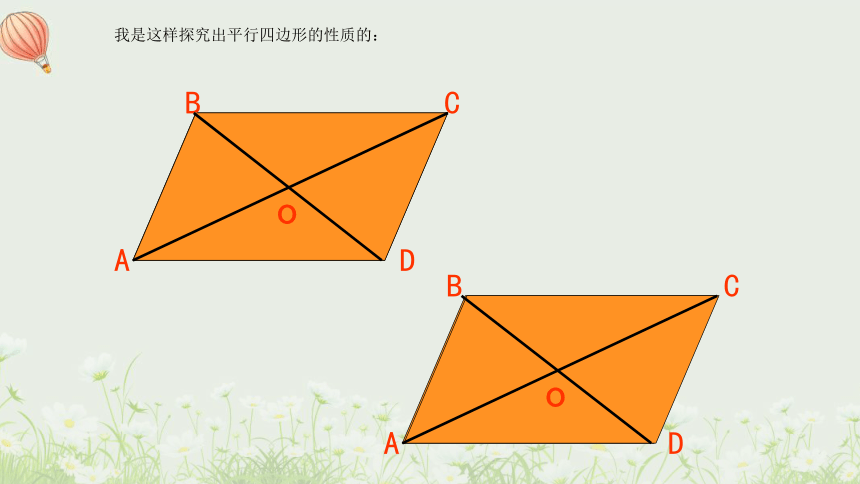
我是这样探究出平行四边形的性质的:
C
O
B
D
A
o
概括证明 ,探究性质:
性质1:平行四边形的对边相等,
性质2:平行四边形的对角相等.
几何语言:
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
几何语言:
∵ 四边形ABCD是平行四边形
∴ ∠A=∠C,∠B=∠D(平行四边形的对角相等)
练习1
1.在 ABCD中, AD=3cm,AB=8cm,
则 ABCD的周长是 cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3. ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
22
10cm,5cm
10
10
练习2
1、在 ABCD中,已知∠A=130°,则∠B=__ ,
∠C=___ ,∠D=___.
A
B
C
D
2、在 ABCD中,若∠A+∠C=200°,则∠A= ;
∠D= 。
50°
50°
130°
80°
100°
应用知识 ,解决问题
例1 如图, ABCD中,DE⊥AB,BF⊥CD,
垂足分别为E、F.
求证:AE=CF.
A
B
C
D
E
F
DE=BF 吗?
┌
┘
练习3:
a
b
c
d
A
B
C
D
已知:a//b,c//d。c,d与a,b分别相交于A,B,C,D四点.
求证:AB=CD
结论1:两条平行线之间的任何两条平行线段都相等。
例2 如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
为什么?
A
B
C
D
b
a
平行线间的距离
结论2:平行线之间的距离处处相等。
┌
┌
应用知识 ,解决问题
例1 如图, ABCD中,DE⊥AB,BF⊥CD,
垂足分别为E、F.
求证:AE=CF.
DE=BF 吗?
A
B
C
D
E
F
┌
┘
提高题:
△ABC是等腰三角形,AB=AC, P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上.
求证:PE+PF=AB.
A
B
C
E
F
P
课堂小结:
通过今天的学习,你知道了平行四边形的哪些性质?
18.1.1 平行四边形的性质(1)
人教版八年级下册
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
定义:两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
几何语言:
(平行四边形的对边平行)
步骤3:沿水平方向平移AB到CD,就得到 ABCD.
A
B
C
D
步骤1:画两条平行线;
步骤2:在两条线上分别取点A和点B,连结AB;
画一画平行四边形:
概括证明 ,探究性质:
活动:在几何图纸上任意画一个平行四边形,观察、测量、思考:
1:平行四边形对边有什么数量关系?
2:平行四边形对角有什么数量关系?
猜想:平行四边形对边相等,对角相等.
你能证明这些结论吗?
概括证明 ,探究性质:
已知: .
求证:
ABCD
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △CDA≌△ABC(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△CDA和△ABC中
证明:连接AC
A
B
C
D
C
O
B
D
A
o
我是这样探究出平行四边形的性质的:
C
O
B
D
A
o
概括证明 ,探究性质:
性质1:平行四边形的对边相等,
性质2:平行四边形的对角相等.
几何语言:
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
几何语言:
∵ 四边形ABCD是平行四边形
∴ ∠A=∠C,∠B=∠D(平行四边形的对角相等)
练习1
1.在 ABCD中, AD=3cm,AB=8cm,
则 ABCD的周长是 cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3. ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
22
10cm,5cm
10
10
练习2
1、在 ABCD中,已知∠A=130°,则∠B=__ ,
∠C=___ ,∠D=___.
A
B
C
D
2、在 ABCD中,若∠A+∠C=200°,则∠A= ;
∠D= 。
50°
50°
130°
80°
100°
应用知识 ,解决问题
例1 如图, ABCD中,DE⊥AB,BF⊥CD,
垂足分别为E、F.
求证:AE=CF.
A
B
C
D
E
F
DE=BF 吗?
┌
┘
练习3:
a
b
c
d
A
B
C
D
已知:a//b,c//d。c,d与a,b分别相交于A,B,C,D四点.
求证:AB=CD
结论1:两条平行线之间的任何两条平行线段都相等。
例2 如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
为什么?
A
B
C
D
b
a
平行线间的距离
结论2:平行线之间的距离处处相等。
┌
┌
应用知识 ,解决问题
例1 如图, ABCD中,DE⊥AB,BF⊥CD,
垂足分别为E、F.
求证:AE=CF.
DE=BF 吗?
A
B
C
D
E
F
┌
┘
提高题:
△ABC是等腰三角形,AB=AC, P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上.
求证:PE+PF=AB.
A
B
C
E
F
P
课堂小结:
通过今天的学习,你知道了平行四边形的哪些性质?
