1.2.2 数 轴 教案 人教版数学七年级上册
文档属性
| 名称 | 1.2.2 数 轴 教案 人教版数学七年级上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 626.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 00:00:00 | ||
图片预览


文档简介
第一章 有理数
1.2 有理数
1.2.2 数轴
一、教学目标
1.掌握数轴的概念,理解数轴上的点和有理数的对应关系.
2.会正确的画出数轴,利用数轴上的点表示有理数.
二、教学重难点
重点:掌握数轴的概念,理解数轴上的点和有理数的对应关系.
难点:会正确的画出数轴,利用数轴上的点表示有理数.
三、教学过程
【新课导入】
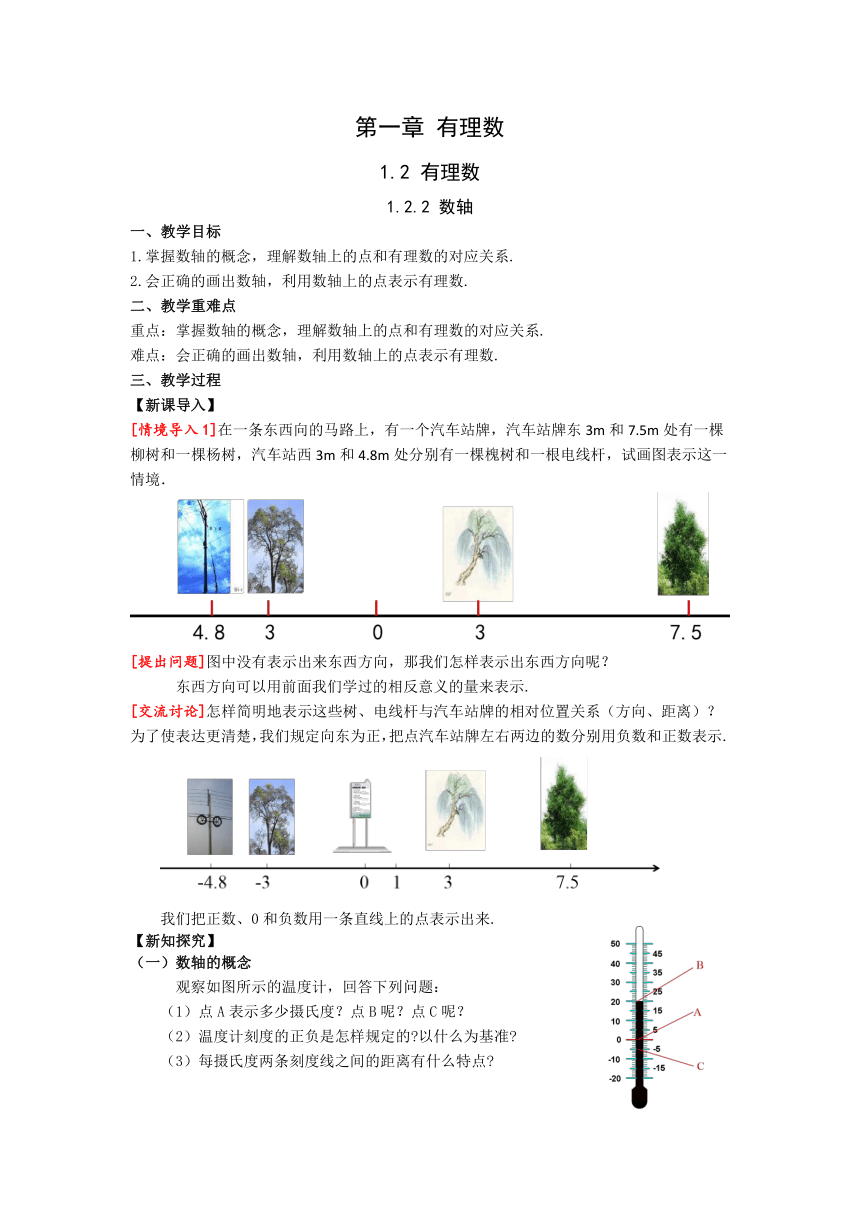
[情境导入1]在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
[提出问题]图中没有表示出来东西方向,那我们怎样表示出东西方向呢?
东西方向可以用前面我们学过的相反意义的量来表示.
[交流讨论]怎样简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
为了使表达更清楚,我们规定向东为正,把点汽车站牌左右两边的数分别用负数和正数表示.
我们把正数、0和负数用一条直线上的点表示出来.
【新知探究】
数轴的概念
观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)温度计刻度的正负是怎样规定的 以什么为基准
(3)每摄氏度两条刻度线之间的距离有什么特点
[交流讨论]把温度计平放,我们能从中发现什么?
思考:你能借鉴温度计,用一条直线上的点表示有理数吗
[归纳总结]画一条水平直线,在直线上取一点表示0,并把这个点叫作原点,选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到下面的数轴.
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
2.规定从原点向右为正方向,那么相反的方向(从原点向左)则为负方向.
3.选择适当的长度为单位长度.
[巩固练习]试一试:判断下面所画数轴是否正确,并说明理由
注意事项:(1)原点、单位长度和正方向三要素缺一不可;(2)直线一般画水平的;
(3)正方向用箭头表示,一般取向右;(4)取单位长度应结合实际需要,但要做到刻度均匀.
[板书]数轴:原点、单位长度和正方向
数轴画法
(二)在数轴上表示有理数
[课件展示]
[提出问题]1.观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,你有什么发现?
2.每个数到原点的距离是多少?由此你又有什么发现?
3.如何用数轴上的点来表示分数或小数?如:1.5,怎样表示.
[典型例题]例1 在所给数轴上画出表示下列各数的点:-5,-2.5, ,0
解:
注意:①把点标在线上;②把数标在点的上方, 以便观看.
[归纳总结]任何一个有理数都可以用数轴上的一个点来表示.
一般地,设a是一个正数,则数轴上表示数a在原点的_右___边,与原点的距离是_a___个单位长度;表示数-a的点在原点的__左__边,与原点的距离是__a__个单位长度.
[典型例题]例2 在下面数轴上,A,B,C,D各点分别表示什么数?
解:(1)A 点表示2;(2) B 点表示0.25;(3)C点表示-0.75;(4) D点表示-1.5
例3 从数轴上表示-1的点出发,向左移动两个单位长度到点B,则点B表示的数是-3 ,再向右移动5个单位长度到达点C,则点C表示的数是 2 .
变式 点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为 ( C )
A.2 B.-6 C.2或-6 D.不同于以上
点A可能向左移,也可能向右移,所以需分情况讨论.
[板书]所有的有理数都可以用数轴上的点来表示.
【课堂小结】
1.数轴的定义:规定了原点、正方向和单位长度的直线叫数轴.
2.数轴的画法.
3.所有的有理数都可以用数轴上的点来表示,原点右边的数是正数,原点左边的数是负数,
0是正负数的分界限.
【课堂训练】
1.下列说法中正确的是( C )
A. 在数轴上的点表示的数不是正数就是负数
B.数轴的长度是有限的
C. 一个有理数总可以在数轴上找到一个表示它的点
D. 所有整数都可以用数轴上的点表示,但分数就不一定能找到表示它的点
2.与原点距离是2.5个单位长度的点所表示的有理数是( C )
A.2.5 B.-2.5 C.±2.5 D.这个数无法确定
3.在数轴上表示数6的点在原点_右___侧,到原点的距离是__6___个单位长度,表示数-8的点在原点的 _左____侧,到原点的距离是__8___个单位长度.表示数6的点到表示数-8的点的距离是__14____个单位长度.
4.在数轴上到表示-2的点相距8个单位长度的点表示的数为____-10或6____.
5.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是0,-2,1,2.5,-3.
6. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5,,,0.
1.2 有理数
1.2.2 数轴
一、教学目标
1.掌握数轴的概念,理解数轴上的点和有理数的对应关系.
2.会正确的画出数轴,利用数轴上的点表示有理数.
二、教学重难点
重点:掌握数轴的概念,理解数轴上的点和有理数的对应关系.
难点:会正确的画出数轴,利用数轴上的点表示有理数.
三、教学过程
【新课导入】
[情境导入1]在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
[提出问题]图中没有表示出来东西方向,那我们怎样表示出东西方向呢?
东西方向可以用前面我们学过的相反意义的量来表示.
[交流讨论]怎样简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
为了使表达更清楚,我们规定向东为正,把点汽车站牌左右两边的数分别用负数和正数表示.
我们把正数、0和负数用一条直线上的点表示出来.
【新知探究】
数轴的概念
观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)温度计刻度的正负是怎样规定的 以什么为基准
(3)每摄氏度两条刻度线之间的距离有什么特点
[交流讨论]把温度计平放,我们能从中发现什么?
思考:你能借鉴温度计,用一条直线上的点表示有理数吗
[归纳总结]画一条水平直线,在直线上取一点表示0,并把这个点叫作原点,选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到下面的数轴.
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
2.规定从原点向右为正方向,那么相反的方向(从原点向左)则为负方向.
3.选择适当的长度为单位长度.
[巩固练习]试一试:判断下面所画数轴是否正确,并说明理由
注意事项:(1)原点、单位长度和正方向三要素缺一不可;(2)直线一般画水平的;
(3)正方向用箭头表示,一般取向右;(4)取单位长度应结合实际需要,但要做到刻度均匀.
[板书]数轴:原点、单位长度和正方向
数轴画法
(二)在数轴上表示有理数
[课件展示]
[提出问题]1.观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,你有什么发现?
2.每个数到原点的距离是多少?由此你又有什么发现?
3.如何用数轴上的点来表示分数或小数?如:1.5,怎样表示.
[典型例题]例1 在所给数轴上画出表示下列各数的点:-5,-2.5, ,0
解:
注意:①把点标在线上;②把数标在点的上方, 以便观看.
[归纳总结]任何一个有理数都可以用数轴上的一个点来表示.
一般地,设a是一个正数,则数轴上表示数a在原点的_右___边,与原点的距离是_a___个单位长度;表示数-a的点在原点的__左__边,与原点的距离是__a__个单位长度.
[典型例题]例2 在下面数轴上,A,B,C,D各点分别表示什么数?
解:(1)A 点表示2;(2) B 点表示0.25;(3)C点表示-0.75;(4) D点表示-1.5
例3 从数轴上表示-1的点出发,向左移动两个单位长度到点B,则点B表示的数是-3 ,再向右移动5个单位长度到达点C,则点C表示的数是 2 .
变式 点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为 ( C )
A.2 B.-6 C.2或-6 D.不同于以上
点A可能向左移,也可能向右移,所以需分情况讨论.
[板书]所有的有理数都可以用数轴上的点来表示.
【课堂小结】
1.数轴的定义:规定了原点、正方向和单位长度的直线叫数轴.
2.数轴的画法.
3.所有的有理数都可以用数轴上的点来表示,原点右边的数是正数,原点左边的数是负数,
0是正负数的分界限.
【课堂训练】
1.下列说法中正确的是( C )
A. 在数轴上的点表示的数不是正数就是负数
B.数轴的长度是有限的
C. 一个有理数总可以在数轴上找到一个表示它的点
D. 所有整数都可以用数轴上的点表示,但分数就不一定能找到表示它的点
2.与原点距离是2.5个单位长度的点所表示的有理数是( C )
A.2.5 B.-2.5 C.±2.5 D.这个数无法确定
3.在数轴上表示数6的点在原点_右___侧,到原点的距离是__6___个单位长度,表示数-8的点在原点的 _左____侧,到原点的距离是__8___个单位长度.表示数6的点到表示数-8的点的距离是__14____个单位长度.
4.在数轴上到表示-2的点相距8个单位长度的点表示的数为____-10或6____.
5.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是0,-2,1,2.5,-3.
6. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5,,,0.
