第2课时《统计与概率—平均数和可能性》-小升初数学第一轮总复习讲练专题讲义课件(共19张PPT)
文档属性
| 名称 | 第2课时《统计与概率—平均数和可能性》-小升初数学第一轮总复习讲练专题讲义课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 760.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 20:20:35 | ||
图片预览






文档简介
(共19张PPT)
小升初第一轮总复习讲练专题
第2课时:平均数和可能性
专题七:统计与概率
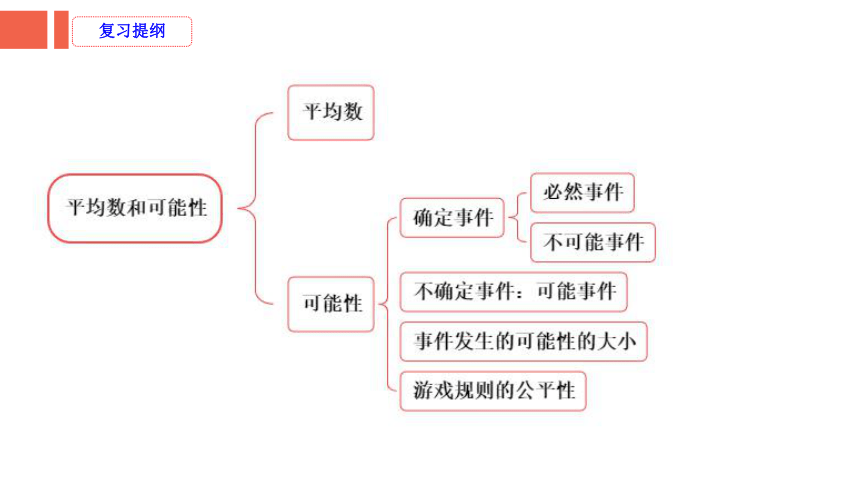
复习提纲
经典案例
考点1:平均数
【例1】某班有40人,期末数学考试有1人缺考,其他同学的平均成绩是87.5分,后来缺考的同学补考后班级的平均成绩提高到87.7分,这个同学的成绩比其他同学的平均成绩高多少分
【解析】本题主要考查平均数的意义以及平均数的求法。因为补考的同学把高出全班平均成绩的部分移补给了其他39人,所以将班级平均成绩从87.5分提高到87.7分,平均成绩提高了87.7-87.5=0.2(分),说明补考的同学共移补给其他同学0.2×39=7.8(分),再加上自己比平均成绩高出的0.2分,则这个同学的成绩比其他同学的平均成绩高7.8+0.2=8(分)。
【解答】(87.7-87.5)×39+(87.7-87.5)=8(分)
答:这个同学的成绩比其他同学的平均成绩高8分。
经典案例
考点1:平均数
强化训练1:
小李参加语文、数学、英语三门科目的测试,语文和英语两科的平均成绩是90分;数学和英语两科的平均成绩是91分;语文和数学两科的平均成绩是95分。小李三门科目的平均成绩是多少分
【解答】
(90×2+91×2+95×2)÷2÷ 3=92(分)
答:小李三门科目的平均成绩是92分。
经典案例
考点2:确定事件和不确定事件
【例2】判断。(对的打“√”,错的打“×”)。
(1)任意抛硬币4次,正面朝上的一定有2次。 ( )
(2)南京的夏天温度可能超过30℃。 ( )
(3)不遵守交通规则,发生事故的可能性很大。 ( )
【解析】(1)抛硬币,正面朝上和反面朝上的可能性是相等的,但发生次数不一定相等。
(2)南京夏天的气温是一个不确定现象,可能超过30℃,也可能不超过30℃。
(3)不遵守交通规则,容易导致交通事故,故发生事故的可能性很大。
【解答】(1)× (2)√ (3)√
经典案例
考点2:确定事件和不确定事件
强化训练2:
【解答】(1)一定 (2)不可能 (3)可能
在( )里填上“一定”“可能”或“不可能”。
(1)三角形的内角和( )是180°。
(2)妹妹的年龄( )比哥哥大。
(3)我们班连续三年运动会获总分第一名今年运动会我们班( )是第一名。
经典案例
考点3:可能性的大小
【例3】盒子里有10个红球、7个白球、3个黄球,球的大小和形状都相同,闭上眼睛从盒子中摸一个球,摸到什么颜色的球的可能性最大
【解析】根据在可能发生的事件中,如果出现该事件的情况较多,则该事件发生的可能性就大的原理,盒子中红球的个数多于白球和黄球的个数,即可作出判断。
【解答】答:摸到红球的可能性最大。
经典案例
考点3:可能性的大小
强化训练3:
【解答】A C
贝贝转动一个转盘20次,指针停在各区域的结果如下表。
贝贝最有可能转动的转盘是( ),
不可能转动的转盘是( )。
经典案例
考点4:游戏规则的公平性
【例4】小明和小强玩摸球游戏,从口袋中任意摸一个球,摸到白球算小明赢,摸到黑球算小强赢。在下面哪些袋子里摸球是公平的 在哪些袋子里摸球是不公平的
【解析】只有当口袋里的两种球的个数相等时,摸到的白球与摸到的黑球的可能性才会相等。所以在D口袋中摸球,游戏才公平,在其他口袋中摸球是不公平的。
【解答】
答:在D口袋中摸球是公平的,在A、B、C口袋中摸球是不公平的。
经典案例
考点4:游戏规则的公平性
强化训练4:
【解答】
(1)不公平,奇数的小球个数较多
(2)不一定
(3)减少一个小球,让奇数和偶数的小球个数一样多
盒子里摆着形状、大小、颜色都相同的9个小球,分别是1~9各数,任意摸一个,摸到偶数小英赢,摸到奇数小明赢。
(1)这个游戏公平吗 为什么
(2)小明一定会赢吗
(3)你能设计一个公平的游戏规则吗
实战演练
重点题型解答
【解答】1.(1)可能 (2)可能 (3)一定 (4) 一定 (5)不可能
2. 2 黑 白 3. 红 黑 4. 84
一、填空
1.用“一定”“可能”或“不可能”填空。
(1)明天( )是晴天。
(2)打开电视,正在播放的( )是《新闻联播》。
(3)两个奇数的和( )是偶数。
(4)明明的哥哥( )比明明大。
(5)袋子里装了8个红球和2个黄球,从中摸出一个,( )摸到白球。
2.盒子里有6个黑球、4个白球,任意摸一个球,有( )种结果,摸到( )球的可能 性大,摸到( )球的可能性小。
3.小红把一个正方体骰子的6个面分别涂上颜色,其中1个面涂黑色,2个面涂白色,其余的面涂红色。把这个骰子掷出后,( )色的面朝上的可能性最大,( )色的面朝上的可能性最小。
4.一次数学测试中,某小组10名学生的成绩分数分别是:100,95,85,80,85,94,66,85,75,75,则这10名学生成绩的平均数是( )分。
实战演练
重点题型解答
5.在右图的口袋中,摸到白球的可能性是( ),
摸到黑球的可能性是( )。要使摸到黑球的可能
性是应再放进( )个( )球。
6.盒子里有两种颜色的乒乓球,小健摸了30次,
每次摸完放回摇匀,情况如下表。盒子里( )
色的乒乓球可能多,( )色的乒乓球可能少。
【解答】5. 3 白 6.黄 白
实战演练
重点题型解答
7.如图,有三个转盘,小月和小亮做转盘游戏,指针停在红色区域算小月赢,停在黄色区域算小亮赢。
(1)想让小月获胜的可能性大,要在( )号转盘上玩。
(2)想让小亮获胜的可能性大,要在( )号转盘上玩。
(3)想让两人获胜的可能性均等,要在( )号转盘上玩。
8.在5个盒子里装了一个糖果,召集全班同学猜一猜糖果在哪个盒子里,猜对的人( ),猜错的人( )。(填“多”或“少”)
【解答】7.(1)③ (2)② (3)① 8.少 多
实战演练
重点题型解答
【解答】 1.× 2.√ 3.√ 4.√ 5.×
二、判断(对的画“√”,错的画“×”)
1.今天下雨,明天一定会出太阳。 ( )
2.太阳一定从东边升起,西边落下。 ( )
3.地球一定绕着太阳转。 ( )
4.任意翻动2022年的台历,翻到星期日的可能性比31号的可能性大。 ( )
5.一次抽奖活动的中奖率是4%,抽100次一定会有4次中奖。 ( )
实战演练
重点题型解答
三、选择(将正确答案的序号填在括号里)
1.做成如右图所示的一个转盘,涂上红、黄、绿三种
颜色,指针转动后落在( )色区域的次数多一些。
A.红 B.黄 C.绿
2.抛一枚硬币,正面朝上的可能性与反面朝上的可能性相比,( )。
A.正面大 B.反面大 C.两面一样大
3.玩游戏时,需要一枚骰子,要使游戏公平进行,应选的骰子是( )。
4.有甲、乙、丙、丁四个数,已知甲、乙、丙三数的平均数是26,丁数是22,四个数的平均数是( )。
A.24 B.25 C.26
5.甲、乙两人做掷骰子游戏,下面( )游戏规则是公平的。
A.小于3的甲赢,否则乙赢 B.质数甲赢,合数乙赢 C.奇数甲赢,偶数乙赢
【解答】1.B 2.C 3.A 4.B 5.C
实战演练
重点题型解答
四、解决问题
1.丁丁、芳芳和冬冬玩游戏,同时将两枚完全相同的硬币上抛一次,落地后如果两枚硬币正面都朝上算丁丁胜,两枚硬币反面都朝上算芳芳胜,一正一反朝上算冬冬胜。谁获胜的可能性大些 为什么
【解答】
答:冬冬获胜的可能性大些。两枚硬币落地可能出现的结果;正正、正反、反正、反反。因为出现一正一反的情况多,有两次,所以冬冬获胜的可能性大些。
实战演练
重点题型解答
2.同学们举办“六一”联欢会,为了活跃气氛在联欢会上要举行抽奖活动。需要把盒子中的红色球设计为一次抽奖摸到的可能性是,黄色球一次抽奖摸到的可能性是;蓝色球一次抽奖摸到的可能性是是。盒子中最少放几个球 每种颜色的球各放几个 请你在下图中画一画并涂上颜色。
【解答】 盒子里至少放10个球。
实战演练
重点题型解答
3.某商人制成了一个如图所示的转盘游戏,取名为“开心大转盘”。游戏规定:参与者自由转动转盘,若指针指向字母“A”,则收费2元;若指 针指向字母“B”,则奖3元;若指针指向字母“C”,则奖1元。一天,前来玩游戏的人转动转盘80次,你认为该商人从中盈利的可能性大还是亏损的可能性大 为什么
【解答】
指向字母A的次数约为:80×50%=40(次)
指向字母B的次数约为:80×12.5%=10(次)
指向字母C 的次数约为:80×37.5%=30(次)
收入:40×2=80(元) 支出:10×3+30×1=60(元)
80>60,所以商人盈利的可能性大
小升初第一轮总复习讲练专题
谢谢观看
小升初第一轮总复习讲练专题
第2课时:平均数和可能性
专题七:统计与概率
复习提纲
经典案例
考点1:平均数
【例1】某班有40人,期末数学考试有1人缺考,其他同学的平均成绩是87.5分,后来缺考的同学补考后班级的平均成绩提高到87.7分,这个同学的成绩比其他同学的平均成绩高多少分
【解析】本题主要考查平均数的意义以及平均数的求法。因为补考的同学把高出全班平均成绩的部分移补给了其他39人,所以将班级平均成绩从87.5分提高到87.7分,平均成绩提高了87.7-87.5=0.2(分),说明补考的同学共移补给其他同学0.2×39=7.8(分),再加上自己比平均成绩高出的0.2分,则这个同学的成绩比其他同学的平均成绩高7.8+0.2=8(分)。
【解答】(87.7-87.5)×39+(87.7-87.5)=8(分)
答:这个同学的成绩比其他同学的平均成绩高8分。
经典案例
考点1:平均数
强化训练1:
小李参加语文、数学、英语三门科目的测试,语文和英语两科的平均成绩是90分;数学和英语两科的平均成绩是91分;语文和数学两科的平均成绩是95分。小李三门科目的平均成绩是多少分
【解答】
(90×2+91×2+95×2)÷2÷ 3=92(分)
答:小李三门科目的平均成绩是92分。
经典案例
考点2:确定事件和不确定事件
【例2】判断。(对的打“√”,错的打“×”)。
(1)任意抛硬币4次,正面朝上的一定有2次。 ( )
(2)南京的夏天温度可能超过30℃。 ( )
(3)不遵守交通规则,发生事故的可能性很大。 ( )
【解析】(1)抛硬币,正面朝上和反面朝上的可能性是相等的,但发生次数不一定相等。
(2)南京夏天的气温是一个不确定现象,可能超过30℃,也可能不超过30℃。
(3)不遵守交通规则,容易导致交通事故,故发生事故的可能性很大。
【解答】(1)× (2)√ (3)√
经典案例
考点2:确定事件和不确定事件
强化训练2:
【解答】(1)一定 (2)不可能 (3)可能
在( )里填上“一定”“可能”或“不可能”。
(1)三角形的内角和( )是180°。
(2)妹妹的年龄( )比哥哥大。
(3)我们班连续三年运动会获总分第一名今年运动会我们班( )是第一名。
经典案例
考点3:可能性的大小
【例3】盒子里有10个红球、7个白球、3个黄球,球的大小和形状都相同,闭上眼睛从盒子中摸一个球,摸到什么颜色的球的可能性最大
【解析】根据在可能发生的事件中,如果出现该事件的情况较多,则该事件发生的可能性就大的原理,盒子中红球的个数多于白球和黄球的个数,即可作出判断。
【解答】答:摸到红球的可能性最大。
经典案例
考点3:可能性的大小
强化训练3:
【解答】A C
贝贝转动一个转盘20次,指针停在各区域的结果如下表。
贝贝最有可能转动的转盘是( ),
不可能转动的转盘是( )。
经典案例
考点4:游戏规则的公平性
【例4】小明和小强玩摸球游戏,从口袋中任意摸一个球,摸到白球算小明赢,摸到黑球算小强赢。在下面哪些袋子里摸球是公平的 在哪些袋子里摸球是不公平的
【解析】只有当口袋里的两种球的个数相等时,摸到的白球与摸到的黑球的可能性才会相等。所以在D口袋中摸球,游戏才公平,在其他口袋中摸球是不公平的。
【解答】
答:在D口袋中摸球是公平的,在A、B、C口袋中摸球是不公平的。
经典案例
考点4:游戏规则的公平性
强化训练4:
【解答】
(1)不公平,奇数的小球个数较多
(2)不一定
(3)减少一个小球,让奇数和偶数的小球个数一样多
盒子里摆着形状、大小、颜色都相同的9个小球,分别是1~9各数,任意摸一个,摸到偶数小英赢,摸到奇数小明赢。
(1)这个游戏公平吗 为什么
(2)小明一定会赢吗
(3)你能设计一个公平的游戏规则吗
实战演练
重点题型解答
【解答】1.(1)可能 (2)可能 (3)一定 (4) 一定 (5)不可能
2. 2 黑 白 3. 红 黑 4. 84
一、填空
1.用“一定”“可能”或“不可能”填空。
(1)明天( )是晴天。
(2)打开电视,正在播放的( )是《新闻联播》。
(3)两个奇数的和( )是偶数。
(4)明明的哥哥( )比明明大。
(5)袋子里装了8个红球和2个黄球,从中摸出一个,( )摸到白球。
2.盒子里有6个黑球、4个白球,任意摸一个球,有( )种结果,摸到( )球的可能 性大,摸到( )球的可能性小。
3.小红把一个正方体骰子的6个面分别涂上颜色,其中1个面涂黑色,2个面涂白色,其余的面涂红色。把这个骰子掷出后,( )色的面朝上的可能性最大,( )色的面朝上的可能性最小。
4.一次数学测试中,某小组10名学生的成绩分数分别是:100,95,85,80,85,94,66,85,75,75,则这10名学生成绩的平均数是( )分。
实战演练
重点题型解答
5.在右图的口袋中,摸到白球的可能性是( ),
摸到黑球的可能性是( )。要使摸到黑球的可能
性是应再放进( )个( )球。
6.盒子里有两种颜色的乒乓球,小健摸了30次,
每次摸完放回摇匀,情况如下表。盒子里( )
色的乒乓球可能多,( )色的乒乓球可能少。
【解答】5. 3 白 6.黄 白
实战演练
重点题型解答
7.如图,有三个转盘,小月和小亮做转盘游戏,指针停在红色区域算小月赢,停在黄色区域算小亮赢。
(1)想让小月获胜的可能性大,要在( )号转盘上玩。
(2)想让小亮获胜的可能性大,要在( )号转盘上玩。
(3)想让两人获胜的可能性均等,要在( )号转盘上玩。
8.在5个盒子里装了一个糖果,召集全班同学猜一猜糖果在哪个盒子里,猜对的人( ),猜错的人( )。(填“多”或“少”)
【解答】7.(1)③ (2)② (3)① 8.少 多
实战演练
重点题型解答
【解答】 1.× 2.√ 3.√ 4.√ 5.×
二、判断(对的画“√”,错的画“×”)
1.今天下雨,明天一定会出太阳。 ( )
2.太阳一定从东边升起,西边落下。 ( )
3.地球一定绕着太阳转。 ( )
4.任意翻动2022年的台历,翻到星期日的可能性比31号的可能性大。 ( )
5.一次抽奖活动的中奖率是4%,抽100次一定会有4次中奖。 ( )
实战演练
重点题型解答
三、选择(将正确答案的序号填在括号里)
1.做成如右图所示的一个转盘,涂上红、黄、绿三种
颜色,指针转动后落在( )色区域的次数多一些。
A.红 B.黄 C.绿
2.抛一枚硬币,正面朝上的可能性与反面朝上的可能性相比,( )。
A.正面大 B.反面大 C.两面一样大
3.玩游戏时,需要一枚骰子,要使游戏公平进行,应选的骰子是( )。
4.有甲、乙、丙、丁四个数,已知甲、乙、丙三数的平均数是26,丁数是22,四个数的平均数是( )。
A.24 B.25 C.26
5.甲、乙两人做掷骰子游戏,下面( )游戏规则是公平的。
A.小于3的甲赢,否则乙赢 B.质数甲赢,合数乙赢 C.奇数甲赢,偶数乙赢
【解答】1.B 2.C 3.A 4.B 5.C
实战演练
重点题型解答
四、解决问题
1.丁丁、芳芳和冬冬玩游戏,同时将两枚完全相同的硬币上抛一次,落地后如果两枚硬币正面都朝上算丁丁胜,两枚硬币反面都朝上算芳芳胜,一正一反朝上算冬冬胜。谁获胜的可能性大些 为什么
【解答】
答:冬冬获胜的可能性大些。两枚硬币落地可能出现的结果;正正、正反、反正、反反。因为出现一正一反的情况多,有两次,所以冬冬获胜的可能性大些。
实战演练
重点题型解答
2.同学们举办“六一”联欢会,为了活跃气氛在联欢会上要举行抽奖活动。需要把盒子中的红色球设计为一次抽奖摸到的可能性是,黄色球一次抽奖摸到的可能性是;蓝色球一次抽奖摸到的可能性是是。盒子中最少放几个球 每种颜色的球各放几个 请你在下图中画一画并涂上颜色。
【解答】 盒子里至少放10个球。
实战演练
重点题型解答
3.某商人制成了一个如图所示的转盘游戏,取名为“开心大转盘”。游戏规定:参与者自由转动转盘,若指针指向字母“A”,则收费2元;若指 针指向字母“B”,则奖3元;若指针指向字母“C”,则奖1元。一天,前来玩游戏的人转动转盘80次,你认为该商人从中盈利的可能性大还是亏损的可能性大 为什么
【解答】
指向字母A的次数约为:80×50%=40(次)
指向字母B的次数约为:80×12.5%=10(次)
指向字母C 的次数约为:80×37.5%=30(次)
收入:40×2=80(元) 支出:10×3+30×1=60(元)
80>60,所以商人盈利的可能性大
小升初第一轮总复习讲练专题
谢谢观看
同课章节目录
