第2课时《图形与几何—平面图形的周长和面积》-小升初数学第一轮总复习讲练专题讲义课件(共18张PPT)
文档属性
| 名称 | 第2课时《图形与几何—平面图形的周长和面积》-小升初数学第一轮总复习讲练专题讲义课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 608.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 20:21:06 | ||
图片预览






文档简介
(共18张PPT)
小升初第一轮总复习讲练专题
第2课时:平面图形的周长
和面积
专题六:图形与几何
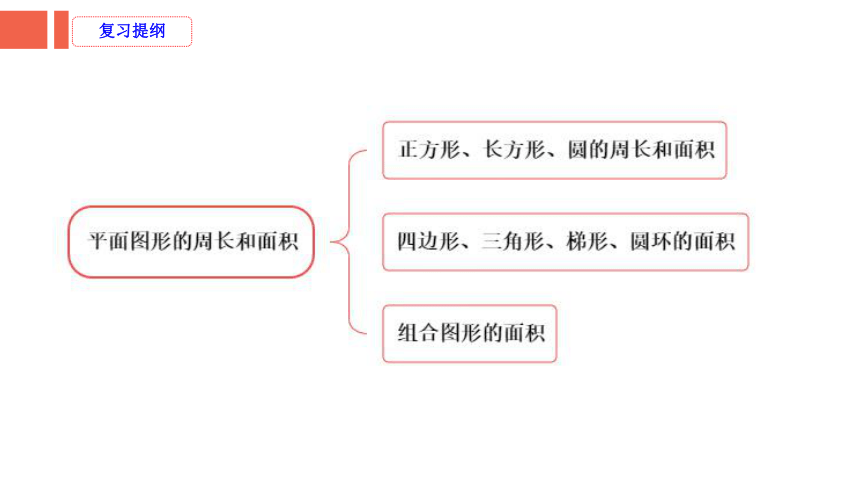
复习提纲
经典案例
考点1:平面图形的周长
【例1】求下图阴影部分的周长。(单位:cm)
【解析】图中阴影部分的周长包括三部分:大圆周长的一半,小圆周长的一半,大圆的半径。图中数据10cm是大圆的半径,又是小圆的直径,先根据π求大圆周长的一半,再根据πd÷2求小圆周长的一半,再把三部分的长度加起来,就是图中阴影部分的周长。
【解答】
3.14×10+3.14×10÷2+10
=31.4+15.7+10
=57.1(cm)
答:阴影部分的周长是57.1cm。
经典案例
考点1:平面图形的周长
强化训练1:
求下列图形的周长。
【解答】
(1)4π÷2+2×2+4=14.28(m)
(2)(2+4+6)π=12π=37.68(cm)
经典案例
考点2:平面图形的面积
【例2】已知下图中阴影部分的面积是24cm ,求梯形的面积。
【解答】
梯形的高:24×2÷12=4(cm)
梯形的面积:(7十12)×4÷2=38(cm )
【解析】此题主要考查三角形和梯形面积公式的灵活运用。阴影部分是一个三角形,已知它的面积是24cm,底是12cm,根据三角形的面积×2÷底=高,可求出三角形的高。三角形的高就是梯形的高,知道梯形上底、下底和高的长度,从而可求出梯形的面积。
经典案例
考点2:平面图形的面积
强化训练2:
李伯伯用100m长的竹篱笆在一块靠墙的空地上围了一个花圃(如图),这个花圃的面积是多少平方米
【解答】(100-30)×30÷2=105(平方米)
答:这个花圃的面积是105平方米。
经典案例
考点3:组合图形的面积
【例3】求图中涂色部分的面积。(单位:cm)
【解析】整个图形的面积,可看作大正方形与右边梯形的面积和,也可看作是两个正方形的面积加上右上角涂色三角形的面积。可通过巧添辅助线把涂色部分拆分成几个三角形的和,或转换位置利用等积变换。
【解答】
连接AK,如图,将涂色部分分为三个三角形。
S三角形EKD=6×(8-6)÷2=6(cm )
S三角形AEK=(8-6)×8÷2=8(cm )
S三角形AKD=6×6÷2=18(cm2)
S涂色部分=6+8+18=32(cm )
经典案例
考点3:组合图形的面积
求阴影部分的面积。(单位:cm)
强化训练3:
【解答】
S阴影=S正方形-S圆
=(2+2)×(2+2)-22π
=16-4π
=16-4×3.14
=16-12.56
=3.44(cm2)
实战演练
重点题型解答
一、填空
1.一个边长是6cm的正方形和一个长是10cm的长方形的周长相等,长方形的宽是( )cm。
2.用3个边长为2cm的正方形拼成一个长方形,这个长方形的周长是( )cm,面积是( )cm。
3.一个三角形的底是20cm,高是6cm,它的面积是( )cm2,与它等底等高的平行四边形的面积是( )cm2。
4.一块梯形广告牌的上底与下底和是40dm,高是12dm,它的面积是( )dm2。
5.一个圆的周长是62.8cm,这个圆的直径是( )cm,面积是( )cm2。
6.在圆形花坛的周围铺一条宽1m的小路。已知花坛的周长是12.56m,则小路的面积是( )m2。
【解答】1. 2 2. 16 12 3. 60 120 4. 240
5. 20 314 6. 15.7
实战演练
重点题型解答
7.下面是贝贝在方格纸上设计的几种图案,每个小方格的面积是1cm,请你写出每种图案的面积。
( ) ( )
8.一个长5cm、宽2.4cm的长方形沿对角线对折后,得
到如图所示的图形,阴影部分的周长是( )cm。
9.一个底边长12cm、面积是48cm2的平行四边形,如果高增加2cm,要使面积不变,底边长应减少( )cm。
【解答】7. 12cm 30.5cm 8. 14.8 9. 4
实战演练
重点题型解答
二、判断(对的画“√”,错的画“×”)
1.周长相等的两个正方形,它们的面积也相等。 ( )
2.等底等高的两个三角形,它们的周长一定相等。 ( )
3.半圆的周长是所在圆周长的一半。 ( )
4.在一个长方形的角上剪去一个小正方形,周长不变。 ( )
5.把一个长方形拉成一个平行四边形后,周长不变,面积变小。 ( )
6.一个三角形的底增加6cm,高增加5cm,则它的面积增加15cm 。 ( )
【解答】1.√ 2.× 3.× 4.√ 5.√ 6.×
实战演练
重点题型解答
【解答】 1.C 2.C 3.A 4.C 5.B
三、选择
1.如图,甲和乙的周长相比,( )。
A.甲长 B.乙长 C.同样长 D.无法比较
2.正方形的边长扩大到原来的3倍,它的面积就扩大到原来的( )倍。
A.3 B.6 C.9 D.不变
3.一个直角三角形的两条直角边分别是8cm和6cm,斜边是10cm。那么斜边上的高是( )。
A.4.8cm B.9.6cm C.2.4cm D.1.2cm
4.如图,甲,乙两个阴影部分的面积相比,( )。
A.甲大 B.乙大 C.同样大 D.无法比较
5.把一张直径4cm的圆形纸片对折两次得到一个扇形,这个扇形的周长是( )cm。
A.4π B.4+π C.π D. π
实战演练
重点题型解答
【解答】
图一:10×11=110(cm2)
图二:100×50÷2+100×36÷2=4300(m2)
四、求下面图形的面积。
实战演练
重点题型解答
五、求下面各图形阴影部分的面积(单位:cm)
【解答】
图一:(20+10)×12÷2-10×12÷2=120(cm )
图二:(5+4)×5÷2=22.5(cm )
图三: ×3.14×(30÷2)2 - ×3.14×(20÷2) =196.25(cm )
实战演练
重点题型解答
六、解决问题。
1.如图是一块长方形草地,长方形的长为16m,宽为10m,中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大
【解答】
(16-2)×(10-2)=112(m)
答:有草部分的面积是112m 。
实战演练
重点题型解答
2.以正方形ABCD的顶点A为圆心,以它的边长为半径画一个圆(如图),已知正方形的面积是12cm2,求涂色部分的面积。
【解答】
3.14×12÷4=9.42(cm ) 12-9.42=2.58(cm2)
答:涂色部分的面积是2.58cm 。
实战演练
重点题型解答
3.如图,有7根半径是6cm的钢管,用一根铁丝把它们捆成一捆,求至少需要多长的铁丝。(接头处忽略不计)
【解答】
3.14×6×2+6×2×6=109.68(cm)
答:至少需要109.68cm长的铁丝。
小升初第一轮总复习讲练专题
谢谢观看
小升初第一轮总复习讲练专题
第2课时:平面图形的周长
和面积
专题六:图形与几何
复习提纲
经典案例
考点1:平面图形的周长
【例1】求下图阴影部分的周长。(单位:cm)
【解析】图中阴影部分的周长包括三部分:大圆周长的一半,小圆周长的一半,大圆的半径。图中数据10cm是大圆的半径,又是小圆的直径,先根据π求大圆周长的一半,再根据πd÷2求小圆周长的一半,再把三部分的长度加起来,就是图中阴影部分的周长。
【解答】
3.14×10+3.14×10÷2+10
=31.4+15.7+10
=57.1(cm)
答:阴影部分的周长是57.1cm。
经典案例
考点1:平面图形的周长
强化训练1:
求下列图形的周长。
【解答】
(1)4π÷2+2×2+4=14.28(m)
(2)(2+4+6)π=12π=37.68(cm)
经典案例
考点2:平面图形的面积
【例2】已知下图中阴影部分的面积是24cm ,求梯形的面积。
【解答】
梯形的高:24×2÷12=4(cm)
梯形的面积:(7十12)×4÷2=38(cm )
【解析】此题主要考查三角形和梯形面积公式的灵活运用。阴影部分是一个三角形,已知它的面积是24cm,底是12cm,根据三角形的面积×2÷底=高,可求出三角形的高。三角形的高就是梯形的高,知道梯形上底、下底和高的长度,从而可求出梯形的面积。
经典案例
考点2:平面图形的面积
强化训练2:
李伯伯用100m长的竹篱笆在一块靠墙的空地上围了一个花圃(如图),这个花圃的面积是多少平方米
【解答】(100-30)×30÷2=105(平方米)
答:这个花圃的面积是105平方米。
经典案例
考点3:组合图形的面积
【例3】求图中涂色部分的面积。(单位:cm)
【解析】整个图形的面积,可看作大正方形与右边梯形的面积和,也可看作是两个正方形的面积加上右上角涂色三角形的面积。可通过巧添辅助线把涂色部分拆分成几个三角形的和,或转换位置利用等积变换。
【解答】
连接AK,如图,将涂色部分分为三个三角形。
S三角形EKD=6×(8-6)÷2=6(cm )
S三角形AEK=(8-6)×8÷2=8(cm )
S三角形AKD=6×6÷2=18(cm2)
S涂色部分=6+8+18=32(cm )
经典案例
考点3:组合图形的面积
求阴影部分的面积。(单位:cm)
强化训练3:
【解答】
S阴影=S正方形-S圆
=(2+2)×(2+2)-22π
=16-4π
=16-4×3.14
=16-12.56
=3.44(cm2)
实战演练
重点题型解答
一、填空
1.一个边长是6cm的正方形和一个长是10cm的长方形的周长相等,长方形的宽是( )cm。
2.用3个边长为2cm的正方形拼成一个长方形,这个长方形的周长是( )cm,面积是( )cm。
3.一个三角形的底是20cm,高是6cm,它的面积是( )cm2,与它等底等高的平行四边形的面积是( )cm2。
4.一块梯形广告牌的上底与下底和是40dm,高是12dm,它的面积是( )dm2。
5.一个圆的周长是62.8cm,这个圆的直径是( )cm,面积是( )cm2。
6.在圆形花坛的周围铺一条宽1m的小路。已知花坛的周长是12.56m,则小路的面积是( )m2。
【解答】1. 2 2. 16 12 3. 60 120 4. 240
5. 20 314 6. 15.7
实战演练
重点题型解答
7.下面是贝贝在方格纸上设计的几种图案,每个小方格的面积是1cm,请你写出每种图案的面积。
( ) ( )
8.一个长5cm、宽2.4cm的长方形沿对角线对折后,得
到如图所示的图形,阴影部分的周长是( )cm。
9.一个底边长12cm、面积是48cm2的平行四边形,如果高增加2cm,要使面积不变,底边长应减少( )cm。
【解答】7. 12cm 30.5cm 8. 14.8 9. 4
实战演练
重点题型解答
二、判断(对的画“√”,错的画“×”)
1.周长相等的两个正方形,它们的面积也相等。 ( )
2.等底等高的两个三角形,它们的周长一定相等。 ( )
3.半圆的周长是所在圆周长的一半。 ( )
4.在一个长方形的角上剪去一个小正方形,周长不变。 ( )
5.把一个长方形拉成一个平行四边形后,周长不变,面积变小。 ( )
6.一个三角形的底增加6cm,高增加5cm,则它的面积增加15cm 。 ( )
【解答】1.√ 2.× 3.× 4.√ 5.√ 6.×
实战演练
重点题型解答
【解答】 1.C 2.C 3.A 4.C 5.B
三、选择
1.如图,甲和乙的周长相比,( )。
A.甲长 B.乙长 C.同样长 D.无法比较
2.正方形的边长扩大到原来的3倍,它的面积就扩大到原来的( )倍。
A.3 B.6 C.9 D.不变
3.一个直角三角形的两条直角边分别是8cm和6cm,斜边是10cm。那么斜边上的高是( )。
A.4.8cm B.9.6cm C.2.4cm D.1.2cm
4.如图,甲,乙两个阴影部分的面积相比,( )。
A.甲大 B.乙大 C.同样大 D.无法比较
5.把一张直径4cm的圆形纸片对折两次得到一个扇形,这个扇形的周长是( )cm。
A.4π B.4+π C.π D. π
实战演练
重点题型解答
【解答】
图一:10×11=110(cm2)
图二:100×50÷2+100×36÷2=4300(m2)
四、求下面图形的面积。
实战演练
重点题型解答
五、求下面各图形阴影部分的面积(单位:cm)
【解答】
图一:(20+10)×12÷2-10×12÷2=120(cm )
图二:(5+4)×5÷2=22.5(cm )
图三: ×3.14×(30÷2)2 - ×3.14×(20÷2) =196.25(cm )
实战演练
重点题型解答
六、解决问题。
1.如图是一块长方形草地,长方形的长为16m,宽为10m,中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大
【解答】
(16-2)×(10-2)=112(m)
答:有草部分的面积是112m 。
实战演练
重点题型解答
2.以正方形ABCD的顶点A为圆心,以它的边长为半径画一个圆(如图),已知正方形的面积是12cm2,求涂色部分的面积。
【解答】
3.14×12÷4=9.42(cm ) 12-9.42=2.58(cm2)
答:涂色部分的面积是2.58cm 。
实战演练
重点题型解答
3.如图,有7根半径是6cm的钢管,用一根铁丝把它们捆成一捆,求至少需要多长的铁丝。(接头处忽略不计)
【解答】
3.14×6×2+6×2×6=109.68(cm)
答:至少需要109.68cm长的铁丝。
小升初第一轮总复习讲练专题
谢谢观看
同课章节目录
