第4课时《数的运算—典型应用题》-小升初数学第一轮总复习讲练专题讲义课件(共31张PPT)
文档属性
| 名称 | 第4课时《数的运算—典型应用题》-小升初数学第一轮总复习讲练专题讲义课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 363.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 20:24:33 | ||
图片预览











文档简介
(共31张PPT)
小升初第一轮总复习讲练专题
第4课时:典型应用题
专题二:数的运算
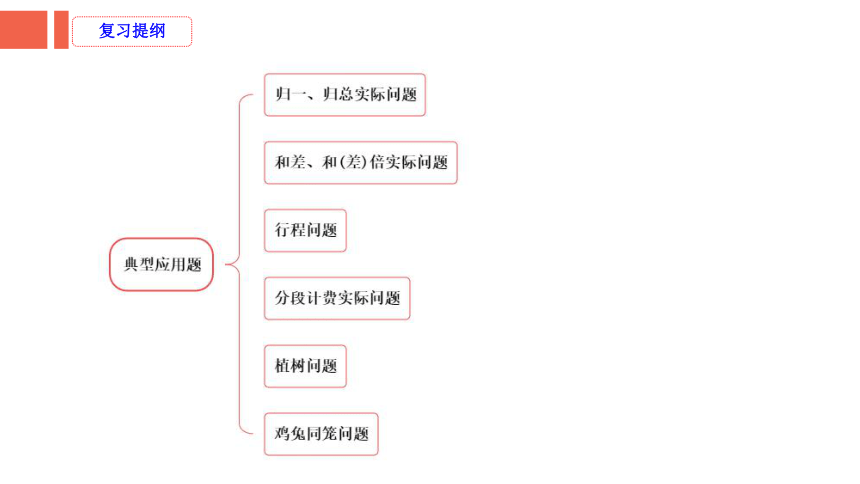
复习提纲
经典案例
考点1:归一问题
【例1】4台织布机8小时织布576m,照这样计算,6台织布机3小时能织完325m布吗
【解答】
576÷4÷8=18(m)
18×6×3=324(m)
324m < 325m
答:6台织布机3小时不能织完325m布。
【解析】这是一道两次归一的应用题(单一量不是一次求出,而是两次求出)。首先根据条件“4台织布机8小时织布576m”可以求出“1台织布机1小时能织布多少米”,再求出6台织布机3小时织布的米数,最后再比较325m与求出的这个数的大小,确定能不能织完。
经典案例
考点1:归一问题
强化训练1:
一辆汽车4小时行了200km,照这样计算,再行2.5小时,一共可行多少千米
【解答】
200+200÷4×2.5
=200+50×2.5
=200+125
=325(千米)
经典案例
考点2:归总问题
【例2】一个工程队要修一条公路,原计划每天修450m,80天完成。现在要求提前20天完成,平均每天应修多少米
【解答】
450×80÷(80-20)
=36000÷60
=600(m)
答:平均每天应修600m。
【解析】这是一道归总应用题。要求平均每天修多少米,首先要求出总量和实际用的天数。总量没有改变,可根据计划求出。实际用的天数比计划提前20天,是比计划少用了20天。
经典案例
考点2:归总问题
强化训练2:
机床厂计划生产75台新机床,每台机床要用3.6t钢材。经过技术革新后,每台机床可节省钢材0.6t。用这批钢材现在可以多生产机床多少台
【解答】
75×3.6÷(3.6-0.6)
=2700÷3
=900(台)
答:剩下的公路平均每天比原来多修筑10米。
经典案例
考点3:和(差)倍问题
【例3】水果店运来苹果的质量是梨的3倍,苹果比梨多160kg,运来梨多少千克
【解答】
160÷(3-1)
=160÷2
=80(kg)
答:运来梨80kg
【解析】根据水果店运来苹果的质量是梨的3倍,把运来梨的质量看作1倍,则运来苹果的质量就是3倍,可知运来革果的质量比梨的质量多3-1=2倍,正好苹果比梨多160kg,用除法求出梨的质量。
经典案例
考点3:和(差)倍问题
妈妈买一套衣服一共用去1650元,上衣的价钱是裤子的2倍。上衣和裤子各是多少元
强化训练3:
【解答】
1 份:1650÷(2+1)=550(元)
裤子:550×1=550(元)
上衣:550×2=1100(元)
答:上衣是1100元,裤子是550元。
经典案例
考点4:行程问题
【例4】甲和乙同时从两地相向而行。甲每分钟行50m,乙每分钟行60m。两人在距离中点50m处相遇,求两地之间的距离。
【解答】
两人的相遇时间:50×2÷(60-50)=10(分)
两地的距离:(60+50)×10=1100(m)
答:两地之间的距离是1100m。
【解析】根据题意,我们可以画线段图如右图:
从图中可以看出,两人相遇时,乙比甲多行了
50×2=100(m)。两人同时出发,为什么乙比甲多行100m呢 因为乙每分钟比甲多行60-50=10(m),100m里有几个10m,就说明两人各行了多少分钟,也就是两人的相遇时间,用两人的速度和乘相遇时间可以求出两地的距离。
经典案例
考点4:行程问题
1.小红从家出发步行去学校,每分钟走60m,走了10分钟后,爸爸从家骑自行车去追小红,结果在距离家900m的地方追上小红。爸爸每分钟行多少米
2.甲、乙两辆汽车同时从A、B两地相对开出,甲车每小时行75km,乙车每小时行65km。甲、乙两车每一次相遇后继续前进,分别到达B、A两地后,立即按原路返回,两车从出发到第二次相遇共行了6小时。A、B两地相距多少千米
强化训练4:
【解答】
(900-60×10)÷60
=(900-600)÷60
=300÷60
=5(分钟)
900÷5=180(米)
答:爸爸每分钟行180米。
【解答】
(75+65)×(6÷3)
=140×2
=280(千米)
答:两地相距280千米.
经典案例
考点5:分段计费问题
【例5】某市出租车计价规则如下:3km以内(包括3km),收费是8元;超过3km的部分,每千米路程收费2.5元。王叔叔去离家6km的某地办事,乘坐出租车需付车费多少元
【解答】
8+(6-3)×2.5
=8+7.5
=15.5(元)
答:乘坐出租车需付车费15.5元。
【解析】本题考查的是分段计算解决费用问题。解题的关键点在于对所行驶的路程进行分段,每段对应不同的收费标准。3km以内(包括3km)共收8元,3km以外的部分共收费(6-3)×2.5=7.5(元)。这两段的费用合起来就是乘坐出租车的总费用。
经典案例
考点5:分段计费问题
东风小学六(3)班48名师生毕业照留念,拍摄费用为14.5元(含5张照片),另外每加印一张1.5元。每人一张照片,一共需要多少元
强化训练5:
【解答】
14.5+1.5×(48-5)
=14.5+1.5×43
=14.5+64.5
=79(元)
答:一共需要79元。
经典案例
考点6:植树问题
【例6】在48m长的河岸一边栽了一排柳树,每两棵树之间的距离都相等,起点和终点都栽了,一共是13棵。相邻的两棵树之间的距离是多少米
【解答】
48÷(13-1)=4(m)
答:相邻的两棵树之间的距离是4m。
【解析】由于两头都栽树,那么间隔数就比棵数少1,因为间隔数=13-1=12(段),由于河岸全长48m,被平均分成12(段),因此每两棵树之间的距离为48÷12=4(m)。
经典案例
考点6:植树问题
1.一座大桥长4500m,在桥的两旁每隔45m安装一块广告牌(两端也要装)。这座桥上一共安装了多少块广告牌
2.公路旁等距离地竖着一排路灯。清晨,王阿姨以一定的速度跑步,她从第1个路灯跑到第7个路灯用了3分钟,如果她以这样 的速度从第1个路灯处向前跑30分钟,那么王阿姨能跑到第几个路灯处
强化训练6:
【解答】
(4500÷45+1)×2
=(100+1)×2
=101×2
=202(块)
答:这座桥上一共安装了202块广告牌。
【解答】
解: 3÷(7-1)=0.5(分钟)
30÷2=15(分钟)
15÷0.5=30(个)
30+1=31(个)
答:王阿姨能跑到第31个路灯处。
经典案例
考点7:鸡兔同笼问题
【例7】鸡免同笼,共有20个头,50条腿,鸡和兔各有多少只
【解答】
假设全是鸡,则共有20×2=40(条)腿。
兔:(50-40)÷(4-2)=5(只)
鸡:20-5=15(只)
答:鸡有15只,兔有5只。
【解析】此题主要考查学生运用“假设法”来解决实际问题的能力。如果把兔看作鸡,则兔子也有2条腿,则20只共有20×2=40(条)腿,比实际的腿少了50-40=10(条),这是因为将兔看作鸡,每只少2条腿,那么多少只兔被看作鸡少10条腿 10÷2=5(只)。这样问题就解决了。
经典案例
考点7:鸡兔同笼问题
1.一名篮球运动员在一场比赛中一共投中9个球,有2分球,也有3分球。已知这名运动员一共得了21分,他投中2分球和3分球各多少个
2.松鼠妈妈采松子,晴天每天可以采20个,雨天每天只能采12个,它一连几天共采了112个松子,平均每天采14个。这几天当中有几天是雨天
强化训练7:
【解答】
假设投中的全部是3分球,
2分球的个数:
(3×9-21)÷(3-2)=6÷1=6(个);
3分球的个数是:9-6=3(个);
答:他投中了6个2分球,3个3分球。
【解答】根据题意可得,它一共采的天数是112÷14=8(天),
根据鸡兔同笼问题中的公式可知,雨天的天数:
(20×8﹣112)÷(20﹣12)
=48÷8,
=6(天);
答:这几天当中有6天有雨.
【解答】 1. 3 2. 12.6 3. 3 4. 945 315 5. 18 12
实战演练
重点题型解答
1.有甲、乙两箱青苹果,甲箱重18kg,乙箱重24kg,从乙箱中拿出( )kg放入甲箱,两箱苹果同样重。
2.买5支铅笔要3.5元钱,买同样的铅笔18支,需要( )元钱。
3.A、B两地相距30km,甲、乙两人同时从A、B两地出发,相向而行,甲每小时行4km,乙每小时行6km,经过( )小时两人相遇。
4.果园里有桃树和梨树一共1260棵,桃树的棵数是梨树的3倍,果园里有桃树( )棵,梨树( )棵。
5.有鸡和兔共30只,共84只脚,鸡有( )只,兔有( )只。
【解答】 1.A 2.B 3.A 4.B
实战演练
重点题型解答
1.小李和小刘在周长为400m的环形跑道上跑步,小李每秒跑5m,小刘每秒跑4m,他们从同一地点同时反向跑,问经过几秒相遇。列式是( )。
A.400÷(5+4) B.400÷(5-4) C.400÷4×5 D.400÷5×4
2.两艘轮船同时从同一港口出发,向相反方向行驶,一艘轮船每小时行24km,另一艘轮船每小时行18km,3小时后两船相距( )km。
A.18 B.126 C.14 D.90
3.一辆汽车从甲地开往乙地,去时每小时行60km,返回时每小时行90km。这辆汽车往返的平均速度是每小时( )km。
A.72 B.75 C.78 D.81
4.小军从一楼走到三楼用6分钟,照这样的速度,他从一楼到九楼要用( )分钟。
A.18 B.24 C.48 D.54
实战演练
重点题型解答
1. 6辆卡车8次可以运输货物576t,照这样计算,10辆同样的卡车12次可以运输货物多少吨
【解答】
576÷6÷8×10×12=1440(t)
答:10辆同样的卡车12次可以运输货物1440t。
实战演练
重点题型解答
2.某毛毯厂原计划30天生产12150条毛毯。由于改进了工艺,结果提前5天完成了任务。实际每天比计划多生产多少条毛毯
【解答】
12150÷(30-5)-12150÷30=81(条)
答:实际每天比计划多生产81条毛毯。
实战演练
重点题型解答
3.一个两层的书架,上层放的书是下层的2.5倍,如果从上层取60本放入下层,则两层书的本数相等,上层原来放书多少本
【解答】
60×2÷(2.5-1)=80(本) 80×2.5=200(本)
答:上层原来放书200本。
实战演练
重点题型解答
4.某市出租车收费标准如下:(不足1km按1km计算),小明乘出租车行驶了4.8km,应付车费多少元
【解答】
6+(5-3)×1.5=9(元)
答:应付车费9元。
实战演练
重点题型解答
5.某广告公司在一条路的一侧每隔50米竖一块广告宣传牌,从起点到终点共竖有10块(头尾各一块),这条道路长多少米
【解答】
50×(10-1)=450(m)
答:这条道路长450 m。
实战演练
重点题型解答
6.小明家离学校880m,他以每分钟80m的速度行走刚好到校上课,但是走了3分钟后,发现自己忘带一本书,必须回家取书,他每分钟走多少米回家取书,再上学不会迟到
【解答】
880÷80=11(分钟) (880+80×3)÷(11-3)=140(m)
答:他每分钟走140m回家取书,再上学才不会迟到。
实战演练
重点题型解答
7.一名篮球运动员在一场比赛中一共投中9个球,有2分球,也有3分球,他一共得了21分,请问他投中2分球和3分球各多少个
【解答】
2分球:(3×9-21)÷(3-2)=6(个)
3分球:9-6=3(个)
答:他投中2分球6个,投中3分球3个。
实战演练
重点题型解答
8.一条笔直的公路一旁原有电线杆46根,它们的间距是12m。现在要改为只架设28根电线杆(两端的杆子不动),间距应设为多少米
【解答】
(46-1)×12÷(28-1)=20(m)
答:间距应设为20m。
实战演练
重点题型解答
9.某城市全面推行阶梯水价,其中居民生活用水的基本水价为每立方米1.8元。具体方案为用水人口为4人及以下用户,月用水量不超过24m ,按基本水价收水费;超过24m 的部分按基本水价的1.3倍收水费。王红家有3口人,5月共交水费73.62元,请你算一算,王红家该月用水多少立方米
【解答】
73.62-24×1.8=30.42(元)
30.42÷(1.8×1.3)+24=37(m)
答:王红家该月用水37m 。
实战演练
重点题型解答
10.育才小学举行一次安全知识竞赛,共20道题,做对一题得10分,做错一题倒扣6分,乐乐得了72分,他做对多少道题
【解答】
做错的题:(20×1072)÷(10+6)=8(道)
做对的题:20-8=12(道)
答:他做对了12道题。
实战演练
重点题型解答
11.甲仓库存粮130t,乙仓库存粮80t。现在又有60t粮食需运入,甲、乙两仓库各运进多少吨才能使甲仓库的存粮吨数是乙仓库的2倍
【解答】
(130+80+60)÷(2+1)=90(t)
甲仓库:90×2-130=50(t)
乙仓库:90-80=10(t)
答:甲仓库运进50t,乙仓库运进10t才能使甲仓库的存粮吨数是乙仓库的2倍。
实战演练
重点题型解答
12.两地相距3km,甲、乙两人同时从两地出发,相向而行。甲每分钟行80m,乙每分钟行70m,如果有只狗与甲同行,狗每分钟跑150m,当狗遇到乙时立即返回,遇到甲后又向乙跑去。这样,狗不停地在甲、乙之间往返跑,直到两人相遇为止。那么狗在两人中间跑的路程是多少米
【解答】
3km=3000m
狗跑的时间:3000÷(80+70)=20(分钟)
狗跑的路程:150×20=3000(m)
答:狗在两人中间跑的路程是3000m。
小升初第一轮总复习讲练专题
谢谢观看
小升初第一轮总复习讲练专题
第4课时:典型应用题
专题二:数的运算
复习提纲
经典案例
考点1:归一问题
【例1】4台织布机8小时织布576m,照这样计算,6台织布机3小时能织完325m布吗
【解答】
576÷4÷8=18(m)
18×6×3=324(m)
324m < 325m
答:6台织布机3小时不能织完325m布。
【解析】这是一道两次归一的应用题(单一量不是一次求出,而是两次求出)。首先根据条件“4台织布机8小时织布576m”可以求出“1台织布机1小时能织布多少米”,再求出6台织布机3小时织布的米数,最后再比较325m与求出的这个数的大小,确定能不能织完。
经典案例
考点1:归一问题
强化训练1:
一辆汽车4小时行了200km,照这样计算,再行2.5小时,一共可行多少千米
【解答】
200+200÷4×2.5
=200+50×2.5
=200+125
=325(千米)
经典案例
考点2:归总问题
【例2】一个工程队要修一条公路,原计划每天修450m,80天完成。现在要求提前20天完成,平均每天应修多少米
【解答】
450×80÷(80-20)
=36000÷60
=600(m)
答:平均每天应修600m。
【解析】这是一道归总应用题。要求平均每天修多少米,首先要求出总量和实际用的天数。总量没有改变,可根据计划求出。实际用的天数比计划提前20天,是比计划少用了20天。
经典案例
考点2:归总问题
强化训练2:
机床厂计划生产75台新机床,每台机床要用3.6t钢材。经过技术革新后,每台机床可节省钢材0.6t。用这批钢材现在可以多生产机床多少台
【解答】
75×3.6÷(3.6-0.6)
=2700÷3
=900(台)
答:剩下的公路平均每天比原来多修筑10米。
经典案例
考点3:和(差)倍问题
【例3】水果店运来苹果的质量是梨的3倍,苹果比梨多160kg,运来梨多少千克
【解答】
160÷(3-1)
=160÷2
=80(kg)
答:运来梨80kg
【解析】根据水果店运来苹果的质量是梨的3倍,把运来梨的质量看作1倍,则运来苹果的质量就是3倍,可知运来革果的质量比梨的质量多3-1=2倍,正好苹果比梨多160kg,用除法求出梨的质量。
经典案例
考点3:和(差)倍问题
妈妈买一套衣服一共用去1650元,上衣的价钱是裤子的2倍。上衣和裤子各是多少元
强化训练3:
【解答】
1 份:1650÷(2+1)=550(元)
裤子:550×1=550(元)
上衣:550×2=1100(元)
答:上衣是1100元,裤子是550元。
经典案例
考点4:行程问题
【例4】甲和乙同时从两地相向而行。甲每分钟行50m,乙每分钟行60m。两人在距离中点50m处相遇,求两地之间的距离。
【解答】
两人的相遇时间:50×2÷(60-50)=10(分)
两地的距离:(60+50)×10=1100(m)
答:两地之间的距离是1100m。
【解析】根据题意,我们可以画线段图如右图:
从图中可以看出,两人相遇时,乙比甲多行了
50×2=100(m)。两人同时出发,为什么乙比甲多行100m呢 因为乙每分钟比甲多行60-50=10(m),100m里有几个10m,就说明两人各行了多少分钟,也就是两人的相遇时间,用两人的速度和乘相遇时间可以求出两地的距离。
经典案例
考点4:行程问题
1.小红从家出发步行去学校,每分钟走60m,走了10分钟后,爸爸从家骑自行车去追小红,结果在距离家900m的地方追上小红。爸爸每分钟行多少米
2.甲、乙两辆汽车同时从A、B两地相对开出,甲车每小时行75km,乙车每小时行65km。甲、乙两车每一次相遇后继续前进,分别到达B、A两地后,立即按原路返回,两车从出发到第二次相遇共行了6小时。A、B两地相距多少千米
强化训练4:
【解答】
(900-60×10)÷60
=(900-600)÷60
=300÷60
=5(分钟)
900÷5=180(米)
答:爸爸每分钟行180米。
【解答】
(75+65)×(6÷3)
=140×2
=280(千米)
答:两地相距280千米.
经典案例
考点5:分段计费问题
【例5】某市出租车计价规则如下:3km以内(包括3km),收费是8元;超过3km的部分,每千米路程收费2.5元。王叔叔去离家6km的某地办事,乘坐出租车需付车费多少元
【解答】
8+(6-3)×2.5
=8+7.5
=15.5(元)
答:乘坐出租车需付车费15.5元。
【解析】本题考查的是分段计算解决费用问题。解题的关键点在于对所行驶的路程进行分段,每段对应不同的收费标准。3km以内(包括3km)共收8元,3km以外的部分共收费(6-3)×2.5=7.5(元)。这两段的费用合起来就是乘坐出租车的总费用。
经典案例
考点5:分段计费问题
东风小学六(3)班48名师生毕业照留念,拍摄费用为14.5元(含5张照片),另外每加印一张1.5元。每人一张照片,一共需要多少元
强化训练5:
【解答】
14.5+1.5×(48-5)
=14.5+1.5×43
=14.5+64.5
=79(元)
答:一共需要79元。
经典案例
考点6:植树问题
【例6】在48m长的河岸一边栽了一排柳树,每两棵树之间的距离都相等,起点和终点都栽了,一共是13棵。相邻的两棵树之间的距离是多少米
【解答】
48÷(13-1)=4(m)
答:相邻的两棵树之间的距离是4m。
【解析】由于两头都栽树,那么间隔数就比棵数少1,因为间隔数=13-1=12(段),由于河岸全长48m,被平均分成12(段),因此每两棵树之间的距离为48÷12=4(m)。
经典案例
考点6:植树问题
1.一座大桥长4500m,在桥的两旁每隔45m安装一块广告牌(两端也要装)。这座桥上一共安装了多少块广告牌
2.公路旁等距离地竖着一排路灯。清晨,王阿姨以一定的速度跑步,她从第1个路灯跑到第7个路灯用了3分钟,如果她以这样 的速度从第1个路灯处向前跑30分钟,那么王阿姨能跑到第几个路灯处
强化训练6:
【解答】
(4500÷45+1)×2
=(100+1)×2
=101×2
=202(块)
答:这座桥上一共安装了202块广告牌。
【解答】
解: 3÷(7-1)=0.5(分钟)
30÷2=15(分钟)
15÷0.5=30(个)
30+1=31(个)
答:王阿姨能跑到第31个路灯处。
经典案例
考点7:鸡兔同笼问题
【例7】鸡免同笼,共有20个头,50条腿,鸡和兔各有多少只
【解答】
假设全是鸡,则共有20×2=40(条)腿。
兔:(50-40)÷(4-2)=5(只)
鸡:20-5=15(只)
答:鸡有15只,兔有5只。
【解析】此题主要考查学生运用“假设法”来解决实际问题的能力。如果把兔看作鸡,则兔子也有2条腿,则20只共有20×2=40(条)腿,比实际的腿少了50-40=10(条),这是因为将兔看作鸡,每只少2条腿,那么多少只兔被看作鸡少10条腿 10÷2=5(只)。这样问题就解决了。
经典案例
考点7:鸡兔同笼问题
1.一名篮球运动员在一场比赛中一共投中9个球,有2分球,也有3分球。已知这名运动员一共得了21分,他投中2分球和3分球各多少个
2.松鼠妈妈采松子,晴天每天可以采20个,雨天每天只能采12个,它一连几天共采了112个松子,平均每天采14个。这几天当中有几天是雨天
强化训练7:
【解答】
假设投中的全部是3分球,
2分球的个数:
(3×9-21)÷(3-2)=6÷1=6(个);
3分球的个数是:9-6=3(个);
答:他投中了6个2分球,3个3分球。
【解答】根据题意可得,它一共采的天数是112÷14=8(天),
根据鸡兔同笼问题中的公式可知,雨天的天数:
(20×8﹣112)÷(20﹣12)
=48÷8,
=6(天);
答:这几天当中有6天有雨.
【解答】 1. 3 2. 12.6 3. 3 4. 945 315 5. 18 12
实战演练
重点题型解答
1.有甲、乙两箱青苹果,甲箱重18kg,乙箱重24kg,从乙箱中拿出( )kg放入甲箱,两箱苹果同样重。
2.买5支铅笔要3.5元钱,买同样的铅笔18支,需要( )元钱。
3.A、B两地相距30km,甲、乙两人同时从A、B两地出发,相向而行,甲每小时行4km,乙每小时行6km,经过( )小时两人相遇。
4.果园里有桃树和梨树一共1260棵,桃树的棵数是梨树的3倍,果园里有桃树( )棵,梨树( )棵。
5.有鸡和兔共30只,共84只脚,鸡有( )只,兔有( )只。
【解答】 1.A 2.B 3.A 4.B
实战演练
重点题型解答
1.小李和小刘在周长为400m的环形跑道上跑步,小李每秒跑5m,小刘每秒跑4m,他们从同一地点同时反向跑,问经过几秒相遇。列式是( )。
A.400÷(5+4) B.400÷(5-4) C.400÷4×5 D.400÷5×4
2.两艘轮船同时从同一港口出发,向相反方向行驶,一艘轮船每小时行24km,另一艘轮船每小时行18km,3小时后两船相距( )km。
A.18 B.126 C.14 D.90
3.一辆汽车从甲地开往乙地,去时每小时行60km,返回时每小时行90km。这辆汽车往返的平均速度是每小时( )km。
A.72 B.75 C.78 D.81
4.小军从一楼走到三楼用6分钟,照这样的速度,他从一楼到九楼要用( )分钟。
A.18 B.24 C.48 D.54
实战演练
重点题型解答
1. 6辆卡车8次可以运输货物576t,照这样计算,10辆同样的卡车12次可以运输货物多少吨
【解答】
576÷6÷8×10×12=1440(t)
答:10辆同样的卡车12次可以运输货物1440t。
实战演练
重点题型解答
2.某毛毯厂原计划30天生产12150条毛毯。由于改进了工艺,结果提前5天完成了任务。实际每天比计划多生产多少条毛毯
【解答】
12150÷(30-5)-12150÷30=81(条)
答:实际每天比计划多生产81条毛毯。
实战演练
重点题型解答
3.一个两层的书架,上层放的书是下层的2.5倍,如果从上层取60本放入下层,则两层书的本数相等,上层原来放书多少本
【解答】
60×2÷(2.5-1)=80(本) 80×2.5=200(本)
答:上层原来放书200本。
实战演练
重点题型解答
4.某市出租车收费标准如下:(不足1km按1km计算),小明乘出租车行驶了4.8km,应付车费多少元
【解答】
6+(5-3)×1.5=9(元)
答:应付车费9元。
实战演练
重点题型解答
5.某广告公司在一条路的一侧每隔50米竖一块广告宣传牌,从起点到终点共竖有10块(头尾各一块),这条道路长多少米
【解答】
50×(10-1)=450(m)
答:这条道路长450 m。
实战演练
重点题型解答
6.小明家离学校880m,他以每分钟80m的速度行走刚好到校上课,但是走了3分钟后,发现自己忘带一本书,必须回家取书,他每分钟走多少米回家取书,再上学不会迟到
【解答】
880÷80=11(分钟) (880+80×3)÷(11-3)=140(m)
答:他每分钟走140m回家取书,再上学才不会迟到。
实战演练
重点题型解答
7.一名篮球运动员在一场比赛中一共投中9个球,有2分球,也有3分球,他一共得了21分,请问他投中2分球和3分球各多少个
【解答】
2分球:(3×9-21)÷(3-2)=6(个)
3分球:9-6=3(个)
答:他投中2分球6个,投中3分球3个。
实战演练
重点题型解答
8.一条笔直的公路一旁原有电线杆46根,它们的间距是12m。现在要改为只架设28根电线杆(两端的杆子不动),间距应设为多少米
【解答】
(46-1)×12÷(28-1)=20(m)
答:间距应设为20m。
实战演练
重点题型解答
9.某城市全面推行阶梯水价,其中居民生活用水的基本水价为每立方米1.8元。具体方案为用水人口为4人及以下用户,月用水量不超过24m ,按基本水价收水费;超过24m 的部分按基本水价的1.3倍收水费。王红家有3口人,5月共交水费73.62元,请你算一算,王红家该月用水多少立方米
【解答】
73.62-24×1.8=30.42(元)
30.42÷(1.8×1.3)+24=37(m)
答:王红家该月用水37m 。
实战演练
重点题型解答
10.育才小学举行一次安全知识竞赛,共20道题,做对一题得10分,做错一题倒扣6分,乐乐得了72分,他做对多少道题
【解答】
做错的题:(20×1072)÷(10+6)=8(道)
做对的题:20-8=12(道)
答:他做对了12道题。
实战演练
重点题型解答
11.甲仓库存粮130t,乙仓库存粮80t。现在又有60t粮食需运入,甲、乙两仓库各运进多少吨才能使甲仓库的存粮吨数是乙仓库的2倍
【解答】
(130+80+60)÷(2+1)=90(t)
甲仓库:90×2-130=50(t)
乙仓库:90-80=10(t)
答:甲仓库运进50t,乙仓库运进10t才能使甲仓库的存粮吨数是乙仓库的2倍。
实战演练
重点题型解答
12.两地相距3km,甲、乙两人同时从两地出发,相向而行。甲每分钟行80m,乙每分钟行70m,如果有只狗与甲同行,狗每分钟跑150m,当狗遇到乙时立即返回,遇到甲后又向乙跑去。这样,狗不停地在甲、乙之间往返跑,直到两人相遇为止。那么狗在两人中间跑的路程是多少米
【解答】
3km=3000m
狗跑的时间:3000÷(80+70)=20(分钟)
狗跑的路程:150×20=3000(m)
答:狗在两人中间跑的路程是3000m。
小升初第一轮总复习讲练专题
谢谢观看
同课章节目录
