第4课时《图形与几何—圆柱和圆锥的认识与测量》-小升初数学第一轮总复习讲练专题讲义课件(共21张PPT)
文档属性
| 名称 | 第4课时《图形与几何—圆柱和圆锥的认识与测量》-小升初数学第一轮总复习讲练专题讲义课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 507.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
小升初第一轮总复习讲练专题
第4课时:圆柱和圆锥的
认识与测量
专题六:图形与几何
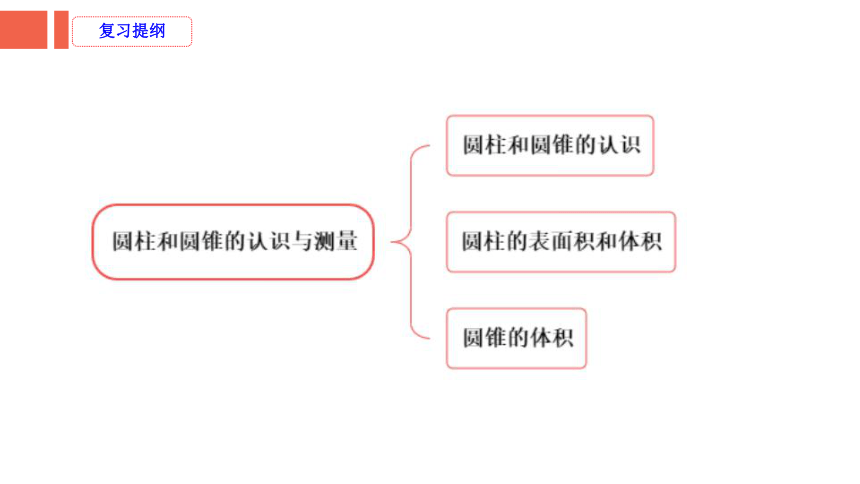
复习提纲
经典案例
考点1:圆柱和圆锥的认识
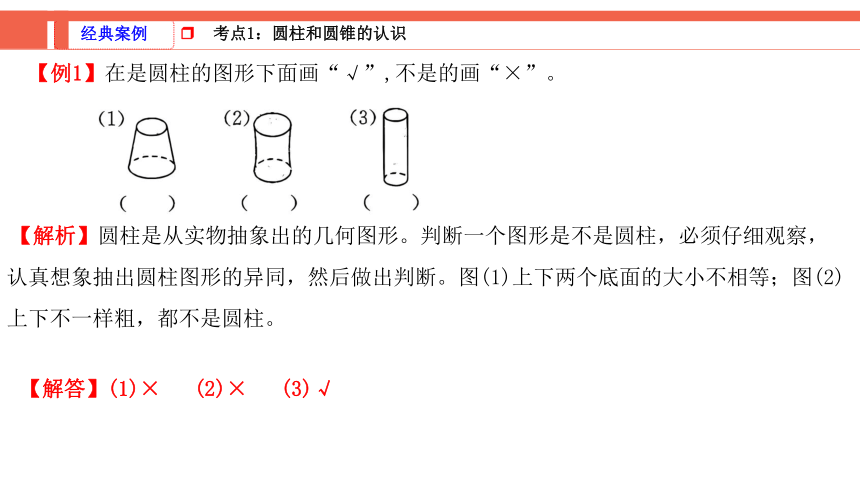
【例1】在是圆柱的图形下面画“√”,不是的画“×”。
【解析】圆柱是从实物抽象出的几何图形。判断一个图形是不是圆柱,必须仔细观察,认真想象抽出圆柱图形的异同,然后做出判断。图(1)上下两个底面的大小不相等;图(2)上下不一样粗,都不是圆柱。
【解答】(1)× (2)× (3)√
经典案例
考点1:圆柱和圆锥的认识
强化训练1:
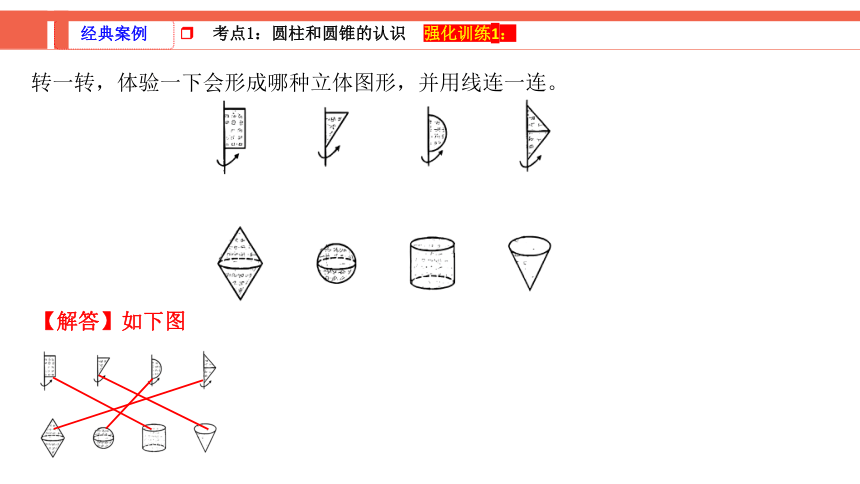
转一转,体验一下会形成哪种立体图形,并用线连一连。
【解答】如下图
经典案例
考点2:圆柱的表面积
【例2】做一个底面半径为20cm、高为50cm的圆柱形铁皮水桶(无盖),需要多少平方厘米的铁皮 (得数保留整百平方厘米)
【解答】
3.14×20 +3.14×2×20×50
=1256+6280
=7536(cm )
≈7600(cm )
答:需要7600cm 的铁皮。
【解析】这是一道已知圆柱底面半径和高,求圆柱表面积的典型例题。首先要明白,求需要多少铁皮,应先求出圆柱形水桶的侧面积,再求一个底面的面积,然后用侧面积加底面积;另外,注意最后的结果取近似值时要用“进一法”
经典案例
考点2:圆柱的表面积
强化训练2:
为了保护环境、节约资源,幸福村倡导使用新能源—沼气。每家每户都砌有一个圆柱形沼气池,底面直径是4m,深是2m。在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米
【解答】
3.14×(4-2)2+3.14×4×2=37.68(m2)
答:抹水泥部分的面积是37.68平方米。
经典案例
考点3:圆柱的体积
【例3】一根圆柱形水泥柱,底面周长是1.884m,高是3m,这根水泥柱的体积是多少立方米
【解析】要求水泥柱的体积,必须求出水泥柱的底面积,可以根据底面周长求出底面半径,进而求出底面积,再用底面积乘高求出体积。
【解答】
3.14×(1.884÷3.14÷2) ×3
=3.14×0.3 ×3
=0.2826×3
=0.8478(m )
答:这根水泥柱的体积是0.8478m 。
经典案例
考点3:圆柱的体积
一个圆柱形柴油桶,它的内直径是4dm,高是6dm,每升柴油重0.86kg,这个油桶能装柴油多少千克 (得数保留一位小数)
强化训练3:
【解答】
4+2=2(分米)
3.14×22×6
=3.14×4 ×6
=3.14 ×24
=75.36(立方分米)
75.36立方分米=75.36升
0.86×75.36≈64.8(千克)
答:这个油桶能装64.8千克柴油.
经典案例
考点4:圆锥的体积
【例4】工地运来的沙堆成一个圆锥形,底面周长是12.56m,高是1.2m,每立方米沙约重1.7t,这堆沙一共约重多少吨 (得数保留整数)
【解析】求这堆沙一共有多重,必须要知道圆锥的体积。根据此题,要想求出圆锥的体积,先要根据圆锥的底面周长求出圆锥的底面半径。
【解答】
×(12.56÷3.14÷2)2×3.14×1.2×1.7
= ×4×3.14×1.2×1.7
=8.5408(t)
≈9t
答:这堆沙一共约重9t。
经典案例
考点4:圆锥的体积
同学们做物体的沉浮实验,将一个底面半径2dm、高3dm的圆锥形铁块浸没在一个盛满水的水桶里,将有多少升的水会溢出桶外
强化训练3:
【解答】
×3.14×22×3
= 12.56(dm3)
=12.56(L)
答:将有12.56升的水会溢出桶外。
实战演练
重点题型解答
一、填空
1.圆柱的侧面沿一条高展开后是一个( )形或( )形,如果展开后是( )形,那么这个圆柱的底面周长和高相等。
2.一个刷油漆的圆柱形滚筒,长是2.5dm,直径是5dm。滚动一周,刷油漆的面积是( )dm 。
3.一个圆柱的底面半径是4cm,高是5cm,这个圆柱的侧面积是( )cm ,表面积是( )cm ,体积是( )cm 。
4.一个圆锥的底面积是12cm ,高是5cm,它的体积是( )cm 。
5.如果一个圆柱的体积是90cm3,那么与它等底等高的圆锥的体积是( )cm ;如果一个圆锥的体积是20cm3,那么与它等底等高的圆柱的体积比它大( )cm 。
【解答】1.长方 正方 正方 2. 39.25 3. 125.6 226.08 251.2
4. 20 5. 30 40
实战演练
重点题型解答
6.把一个底面直径是8cm的圆柱分成若干等份,拼成一个近似的长方体,表面积比原来增加了80cm ,这个圆柱原来的体积是( )cm
7.把一根长14dm的圆柱形钢材切成3个大小相同的小圆柱,表面积比原来增加了24dm ,这根钢材原来的体积是( )dm 。
8.一根自来水管的内直径是2cm,水管内水的流速是10cm/s。一位同学洗完手后忘记关水龙头,5分钟浪费了( )L水。
【解答】6. 502.4 7. 84 8. 9.42
实战演练
重点题型解答
二、判断(对的画“√”,错的画“×”)
1.长方体、正方体和圆柱的体积都可以用底面积乘高来计算。 ( )
2.“做一根圆柱形通风管需要多少铁皮”是求这个圆柱的侧面积。 ( )
3.如果两个圆柱的侧面积相等,那么它们的体积也一定相等。 ( )
4.圆锥体积是圆柱体积。 ( )
5.用一张长方形纸围成一个圆柱(无重叠)无论怎样围,这个圆柱的侧面积都不变。 ( )
6.圆柱的底面积不变,高扩大到原来的3倍,体积也扩大到原来的3倍。 ( )
7.一个圆锥的高不变,底面半径扩大到原来的2倍,这个圆锥的体积也扩大到原来的2倍。( )
【解答】1.√ 2.√ 3.× 4.× 5.√ 6.√ 7.×
实战演练
重点题型解答
【解答】 1.C 2.B 3.A
三、选择
1.下图中,以直线为轴旋转,可以得到的圆锥的是( )。
2.一个圆柱的高扩大到原来的3倍,底面半径缩小到原来的 ,圆柱的体积( )。
A.扩大到原来的3倍 B.缩小到原来
C.扩大到原来的9倍 D.缩小到原来
3.一个圆柱和一个圆锥等底等高,体积相差100dm ,圆锥的体积是( )dm 。
A.50 B.100 C.150 D.
实战演练
重点题型解答
【解答】 4.C 5.B 6.C
三、选择
4.体积和高都相等的圆柱和圆锥,它们的底面积之比是( ).
A.1:1 B.3:1 C.1:3 D.9:1
5.一个圆锥的体积是628dm ,底面直径是20dm,它的高应是( )dm。
A.2 B.6 C.18 D.20
6.有一根半径是4dm的圆柱形木料,把这根木料沿高锯成相等的两部分后,表面积比原来增加了128dm 。原来这根木料的高是( )dm。
A.2 B.3 C.8 D.20
实战演练
重点题型解答
【解答】
表面积:3.14×(4+8)×10+3.14×[(8÷2) -(4÷2) ]×2=452.16(cm )
体积:3.14×[(8÷2) -(4÷2) ]×10=376.8(cm )
四、求下面图形的表面积和体积(单位:cm)
实战演练
重点题型解答
五、计算下面图形的体积。(单位:cm)
【解答】
3.14×(4÷2)2+ ×3.14×(4÷2)2×3=37.68(cm )
实战演练
重点题型解答
六、解决问题。
1.如图所示的圆柱,如果高增加2cm,表面积就增加25.12cm ,你能求出原来圆柱的表面积吗
【解答】
25.12÷2=12.56(cm)
12.56÷3.14÷2=2(cm) 3.14×22×2+12.56×6=100.48(cm )
答:原来圆柱的表面积是100.48cm 。
实战演练
重点题型解答
2.如下图,贝贝用一瓶净含量是600mL的纯净水来测量一个瓶身是圆柱形的玻璃瓶的容积,她先将这瓶纯净水全部倒入瓶中,测得水深15cm。然后把瓶口封好,使瓶口向下,这时测得水面距瓶底8cm。请你根据贝贝获得的数据计算玻璃瓶的容积。
【解答】
600mL=600cm
600÷15=40(cm )
40×(15+8)=920(cm )=920(mL)
答:玻璃瓶的容积是920mL。
实战演练
重点题型解答
3.一个圆柱形玻璃容器,从里面量,底面直径是20cm,容器中水面距杯口3cm。将一个底面积为162cm 的圆锥形铅锤完全浸入水中,水会溢出30mL。这个圆锥形铅锤的高是多少
【解答】
30mL=30cm
3.14×(20÷2) ×3+30=972(cm )
972÷( )=18(cm)
答:这个圆锥形铅锤的高是18cm。
小升初第一轮总复习讲练专题
谢谢观看
小升初第一轮总复习讲练专题
第4课时:圆柱和圆锥的
认识与测量
专题六:图形与几何
复习提纲
经典案例
考点1:圆柱和圆锥的认识
【例1】在是圆柱的图形下面画“√”,不是的画“×”。
【解析】圆柱是从实物抽象出的几何图形。判断一个图形是不是圆柱,必须仔细观察,认真想象抽出圆柱图形的异同,然后做出判断。图(1)上下两个底面的大小不相等;图(2)上下不一样粗,都不是圆柱。
【解答】(1)× (2)× (3)√
经典案例
考点1:圆柱和圆锥的认识
强化训练1:
转一转,体验一下会形成哪种立体图形,并用线连一连。
【解答】如下图
经典案例
考点2:圆柱的表面积
【例2】做一个底面半径为20cm、高为50cm的圆柱形铁皮水桶(无盖),需要多少平方厘米的铁皮 (得数保留整百平方厘米)
【解答】
3.14×20 +3.14×2×20×50
=1256+6280
=7536(cm )
≈7600(cm )
答:需要7600cm 的铁皮。
【解析】这是一道已知圆柱底面半径和高,求圆柱表面积的典型例题。首先要明白,求需要多少铁皮,应先求出圆柱形水桶的侧面积,再求一个底面的面积,然后用侧面积加底面积;另外,注意最后的结果取近似值时要用“进一法”
经典案例
考点2:圆柱的表面积
强化训练2:
为了保护环境、节约资源,幸福村倡导使用新能源—沼气。每家每户都砌有一个圆柱形沼气池,底面直径是4m,深是2m。在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米
【解答】
3.14×(4-2)2+3.14×4×2=37.68(m2)
答:抹水泥部分的面积是37.68平方米。
经典案例
考点3:圆柱的体积
【例3】一根圆柱形水泥柱,底面周长是1.884m,高是3m,这根水泥柱的体积是多少立方米
【解析】要求水泥柱的体积,必须求出水泥柱的底面积,可以根据底面周长求出底面半径,进而求出底面积,再用底面积乘高求出体积。
【解答】
3.14×(1.884÷3.14÷2) ×3
=3.14×0.3 ×3
=0.2826×3
=0.8478(m )
答:这根水泥柱的体积是0.8478m 。
经典案例
考点3:圆柱的体积
一个圆柱形柴油桶,它的内直径是4dm,高是6dm,每升柴油重0.86kg,这个油桶能装柴油多少千克 (得数保留一位小数)
强化训练3:
【解答】
4+2=2(分米)
3.14×22×6
=3.14×4 ×6
=3.14 ×24
=75.36(立方分米)
75.36立方分米=75.36升
0.86×75.36≈64.8(千克)
答:这个油桶能装64.8千克柴油.
经典案例
考点4:圆锥的体积
【例4】工地运来的沙堆成一个圆锥形,底面周长是12.56m,高是1.2m,每立方米沙约重1.7t,这堆沙一共约重多少吨 (得数保留整数)
【解析】求这堆沙一共有多重,必须要知道圆锥的体积。根据此题,要想求出圆锥的体积,先要根据圆锥的底面周长求出圆锥的底面半径。
【解答】
×(12.56÷3.14÷2)2×3.14×1.2×1.7
= ×4×3.14×1.2×1.7
=8.5408(t)
≈9t
答:这堆沙一共约重9t。
经典案例
考点4:圆锥的体积
同学们做物体的沉浮实验,将一个底面半径2dm、高3dm的圆锥形铁块浸没在一个盛满水的水桶里,将有多少升的水会溢出桶外
强化训练3:
【解答】
×3.14×22×3
= 12.56(dm3)
=12.56(L)
答:将有12.56升的水会溢出桶外。
实战演练
重点题型解答
一、填空
1.圆柱的侧面沿一条高展开后是一个( )形或( )形,如果展开后是( )形,那么这个圆柱的底面周长和高相等。
2.一个刷油漆的圆柱形滚筒,长是2.5dm,直径是5dm。滚动一周,刷油漆的面积是( )dm 。
3.一个圆柱的底面半径是4cm,高是5cm,这个圆柱的侧面积是( )cm ,表面积是( )cm ,体积是( )cm 。
4.一个圆锥的底面积是12cm ,高是5cm,它的体积是( )cm 。
5.如果一个圆柱的体积是90cm3,那么与它等底等高的圆锥的体积是( )cm ;如果一个圆锥的体积是20cm3,那么与它等底等高的圆柱的体积比它大( )cm 。
【解答】1.长方 正方 正方 2. 39.25 3. 125.6 226.08 251.2
4. 20 5. 30 40
实战演练
重点题型解答
6.把一个底面直径是8cm的圆柱分成若干等份,拼成一个近似的长方体,表面积比原来增加了80cm ,这个圆柱原来的体积是( )cm
7.把一根长14dm的圆柱形钢材切成3个大小相同的小圆柱,表面积比原来增加了24dm ,这根钢材原来的体积是( )dm 。
8.一根自来水管的内直径是2cm,水管内水的流速是10cm/s。一位同学洗完手后忘记关水龙头,5分钟浪费了( )L水。
【解答】6. 502.4 7. 84 8. 9.42
实战演练
重点题型解答
二、判断(对的画“√”,错的画“×”)
1.长方体、正方体和圆柱的体积都可以用底面积乘高来计算。 ( )
2.“做一根圆柱形通风管需要多少铁皮”是求这个圆柱的侧面积。 ( )
3.如果两个圆柱的侧面积相等,那么它们的体积也一定相等。 ( )
4.圆锥体积是圆柱体积。 ( )
5.用一张长方形纸围成一个圆柱(无重叠)无论怎样围,这个圆柱的侧面积都不变。 ( )
6.圆柱的底面积不变,高扩大到原来的3倍,体积也扩大到原来的3倍。 ( )
7.一个圆锥的高不变,底面半径扩大到原来的2倍,这个圆锥的体积也扩大到原来的2倍。( )
【解答】1.√ 2.√ 3.× 4.× 5.√ 6.√ 7.×
实战演练
重点题型解答
【解答】 1.C 2.B 3.A
三、选择
1.下图中,以直线为轴旋转,可以得到的圆锥的是( )。
2.一个圆柱的高扩大到原来的3倍,底面半径缩小到原来的 ,圆柱的体积( )。
A.扩大到原来的3倍 B.缩小到原来
C.扩大到原来的9倍 D.缩小到原来
3.一个圆柱和一个圆锥等底等高,体积相差100dm ,圆锥的体积是( )dm 。
A.50 B.100 C.150 D.
实战演练
重点题型解答
【解答】 4.C 5.B 6.C
三、选择
4.体积和高都相等的圆柱和圆锥,它们的底面积之比是( ).
A.1:1 B.3:1 C.1:3 D.9:1
5.一个圆锥的体积是628dm ,底面直径是20dm,它的高应是( )dm。
A.2 B.6 C.18 D.20
6.有一根半径是4dm的圆柱形木料,把这根木料沿高锯成相等的两部分后,表面积比原来增加了128dm 。原来这根木料的高是( )dm。
A.2 B.3 C.8 D.20
实战演练
重点题型解答
【解答】
表面积:3.14×(4+8)×10+3.14×[(8÷2) -(4÷2) ]×2=452.16(cm )
体积:3.14×[(8÷2) -(4÷2) ]×10=376.8(cm )
四、求下面图形的表面积和体积(单位:cm)
实战演练
重点题型解答
五、计算下面图形的体积。(单位:cm)
【解答】
3.14×(4÷2)2+ ×3.14×(4÷2)2×3=37.68(cm )
实战演练
重点题型解答
六、解决问题。
1.如图所示的圆柱,如果高增加2cm,表面积就增加25.12cm ,你能求出原来圆柱的表面积吗
【解答】
25.12÷2=12.56(cm)
12.56÷3.14÷2=2(cm) 3.14×22×2+12.56×6=100.48(cm )
答:原来圆柱的表面积是100.48cm 。
实战演练
重点题型解答
2.如下图,贝贝用一瓶净含量是600mL的纯净水来测量一个瓶身是圆柱形的玻璃瓶的容积,她先将这瓶纯净水全部倒入瓶中,测得水深15cm。然后把瓶口封好,使瓶口向下,这时测得水面距瓶底8cm。请你根据贝贝获得的数据计算玻璃瓶的容积。
【解答】
600mL=600cm
600÷15=40(cm )
40×(15+8)=920(cm )=920(mL)
答:玻璃瓶的容积是920mL。
实战演练
重点题型解答
3.一个圆柱形玻璃容器,从里面量,底面直径是20cm,容器中水面距杯口3cm。将一个底面积为162cm 的圆锥形铅锤完全浸入水中,水会溢出30mL。这个圆锥形铅锤的高是多少
【解答】
30mL=30cm
3.14×(20÷2) ×3+30=972(cm )
972÷( )=18(cm)
答:这个圆锥形铅锤的高是18cm。
小升初第一轮总复习讲练专题
谢谢观看
同课章节目录
