第五单元:可能性(单元复习课件)-沪教版五年级数学下册(共27张PPT)
文档属性
| 名称 | 第五单元:可能性(单元复习课件)-沪教版五年级数学下册(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 20:44:03 | ||
图片预览








文档简介
(共27张PPT)
可能性
单元复习
沪教版五年级数学下册
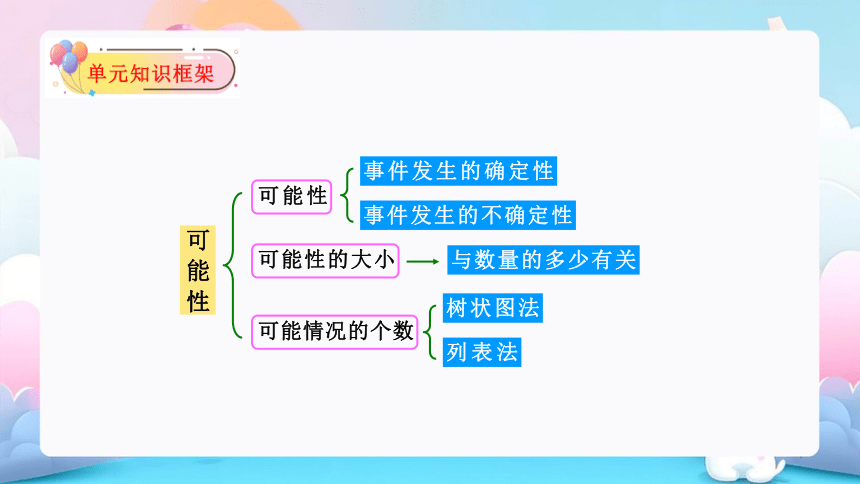
可能性
可能性的大小
可能情况的个数
可能性
事件发生的确定性
与数量的多少有关
可能性
可能性的大小
事件发生的不确定性
可能情况的个数
树状图法
列表法
1、可能性的定义:
在客观事物中,
(1)确定会发生,用“一定”表示;
(2)确定不会发生,用“不可能”表示;
(3)不确定是否发生,用“可能”表示。
这就是事物发生的可能性。
可能性
【例1】在括号里填上“一定”“可能”或“不可能”。
(1)强强比兵兵大3岁,但是强强身高却比兵兵矮2厘米。( )
这句话描述的是两个人年龄和身高的比较情况,是一个客观事实。强强比兵兵大3岁,但是身高却比兵兵矮2厘米,这件事可能发生。
可能
【例1】在括号里填上“一定”“可能”或“不可能”。
(2)在标有1~20的十张卡片中随意摸出2张卡片,两张卡片的和是40。( )
从1到10中,两个最大的数19和20的和是39,不可能出现和为40,所以在标有1~20的十张卡片中随意摸出2张卡片,两张卡片的和不可能是40。
不可能
【例1】在括号里填上“一定”“可能”或“不可能”。
(3)铁和木头都能浮在水面上。( )
铁的密度大于水,通常情况下铁会下沉,而木头有可能浮在水面上,所以这句话是不可能的。
不可能
【例2】把5个红球和3个黄球放在同一个盒子里,任意摸出一个球,( )是白色的。
A.一定 B.可能 C.不可能
因为盒子里只有红球和黄球,根本没有白球,所以不可能摸出白球。
C
【例3】下面的事件一定会发生的是( )。
A. 下个月会下雪
B. 明天太阳会从东方升起
C. 掷骰子掷出7点
A选项下个月是否会下雪具有不确定性,不是一定会发生;
B选项太阳每天都会从东方升起,这是自然规律,是一定会发生的;
C选项骰子只有1到6点,不可能掷出7点。所以一定发生的是B选项。
B
【例4】下面说法正确的是( )。
A. 小王掷骰子,连续5次都是六点,如果再掷一次,那么肯定是六点。
B. 每天都一定有24个小时。
C. 天上出现乌云,意味着肯定要下雨了。
A选项,每次掷骰子的结果都是独立的、随机的,之前连续5次六点,下一次仍有可能是六点,但不是肯定是六点,A选项错误;
B选项,一天就是24个小时,这是确定的,B选项正确;
C选项,天上出现乌云只是有可能下雨,不是肯定要下雨,C选项错误。
B
事件发生的可能性是有大小的。
事件随机出现的可能性的大小与个体数量的多少有关。
个体在总数量中所占数量越多,出现的可能性就越大;
反之,可能性就越小。
可能性的大小
【例5】从1~4四张数字卡片中依次抽出两张,所得数字之和是( )的可能性最大。
从 1、2、3、4中依次抽出两张,所有可能的情况有:1和2、1和3、1和4、2和3、2和4、3和4,它们的和分别是3、4、5、5、6、7其中和为5的情况有2种,出现的次数最多,所以所得数字之和是5的可能性最大。
5
【例6】盒子里有红、白、蓝三种颜色的小球共 25 个,它们除颜色外都相同。任意摸一个球,要使摸到红球的可能性最小,那么盒中最多有( )个红球。
要使摸到红球的可能性最小,红球数量应最少,让白球和蓝球数量尽量多且接近,25÷3=8……1,即平均每种颜色8个还余1个,把余下的1个给白球或蓝球,那么白球和蓝球各9个,红球最多7个。
7
【例7】盒子里有8个球,除颜色外完全相同,在( )条件下,摸出黑球的可能性大。
A.5黑3白 B.2黑6白 C.3黑5白
要摸出黑球可能性大,黑球数量要多于白球数量。
A选项黑球5个多于白球3个,满足条件;
B选项黑球2个少于白球6个,不符合;
C选项黑球3个少于白球5个,不符合。所以答案选A。
A
【例8】从三张分别写有5、7和9数字的纸中任意抽出两张,它们的差是( )的可能性最大。
从 5、7、9 中任意抽出两张,会出现5和7、5和9、7和9三种情况,它们的差分别是:7-5=2,9-5=4,9-7=2,差是2出现了两次,所以差是2的可能性最大。
2
【例9】下面每个盒子里都有 10 个大小相同的球,一定可以摸出蓝球的是( )。
A.8个红球,2个蓝球 B.10个黄球 C.10个蓝球
要想一定摸出某种颜色的球,那么盒子中必须全部都是这种颜色的球。选项A中既有红球又有蓝球,不一定能摸出蓝球;选项B中都是黄球,不可能摸出蓝球;选项C中全是蓝球,所以一定可以摸出蓝球。
C
【例10】从 3,4,5三张数卡中任抽两张,组成一个两位数,如果组成的是质数则兵兵赢,组成的是合数则贝贝赢,这个游戏规则公平吗?
从3,4,5三张数卡中任抽两张组成两位数有34、35、43、45、53、54共6个。其中质数有43,53共2个;合数有34,35,45,54共4个,抽到质数和合数的可能性不同,所以这个游戏规则不公平。
【例11】甲、乙两人轮流掷小正方体,约定红面朝上算甲赢1分,黄面朝上算乙赢1分。用下面( )的小正方体掷是最公平的。
A. 3红3黄 B. 4红2黄 C. 2红4黄 D. 1红5黄
公平的关键在于红面和黄面出现的概率相同,即红面和黄面的数量要相同。
A选项红面和黄面都有3个,数量相等,公平;
B选项红面4个,黄面2个,数量不同,不公平;
C选项红面2个,黄面4个,数量不同,不公平;
D选项红面1个,黄面5个,数量不同,不公平。所以选A。
A
【例12】奇奇和亮亮用摸球游戏来决定谁先开始打篮球,摸到黄球小明先开始,摸到蓝球小亮先开始,在下面( )盒子中摸最公平。A.黄球8个,蓝球2个
B.黄球5个,蓝球5个
C.黄球3个,蓝球7个
要使游戏公平,那么盒子中两种颜色球的数量应该相等。
A选项黄球比蓝球多很多,不公平;
C选项蓝球比黄球多很多,不公平;
只有B选项黄球和蓝球数量相等,是公平的。
B
可能情况的个数
为了不重复、不遗漏地列出所有可能出现的结果,可以借助树状图或列表等方法找出事件所有可能出现的结果;再根据每种结果出现的次数,判断哪种结果出现的可能性最大。
【例13】盒子里有3个红球,2个蓝球(球除颜色外完全相同),一次摸出两个球,可能有( )种结果。
一次摸两个球,可能出现的情况有:两个红球、两个蓝球、一个红球和一个蓝球,共3种情况。
3
【例14】从标有数字1、2、3、4的四张牌中任意抽 2张,可以组成( )个不同两位数。
当抽中1和2时,可以组成12和21;
当抽中1和3时,可以组成13和31;
当抽中1和4时,可以组成14和41;
当抽中2和3时,可以组成23和32;
当抽中2和4时,可以组成24和42;
当抽中3和4时,可以组成34和43,共12个不同的两位数。
12
【例15】从红、黄、蓝、绿、白五种颜色中选出两种,有多少种不同的选法?
从五种颜色中选两种,可以用列举法。
先选红色,那么可以和黄、蓝、绿、白分别组合,有4种选法;
再选黄色,因为和红色已经组合过了,所以可以和蓝、绿、白组合,有3种选法;
接着选蓝色,和绿、白组合,有2种选法;
然后选绿色,和白组合,有1种选法。
将所有选法相加:4+3+2+1=10(种)。
1、甲、乙和小丙三人在玩“石头、剪刀、布”的游戏,下面说法正确的是( )。
A.甲可能赢
B.乙一定赢
C.丙一定输
A
2、盒子中有3张20元和2张50元纸币,从盒子中任意摸出两张,下面说法正确的是( )。
A. 总钱数一定是70元
B. 总钱数可能是40元
C. 总钱数不可能是100元
D. 总钱数可能是120元
B
3、一个盒子装有大小形状完全相同的黑球4个,绿球5个,紫球3个,摸到黑球鸣鸣赢,摸到绿球港港赢,为使游戏公平,盒子中应( )。
A.加入1个黑球
B.加入2个紫球
C.加入1个绿球
D.拿出3个紫球
A
每一份努力,都将在学习中得到最好的回报。加油!
可能性
单元复习
沪教版五年级数学下册
可能性
可能性的大小
可能情况的个数
可能性
事件发生的确定性
与数量的多少有关
可能性
可能性的大小
事件发生的不确定性
可能情况的个数
树状图法
列表法
1、可能性的定义:
在客观事物中,
(1)确定会发生,用“一定”表示;
(2)确定不会发生,用“不可能”表示;
(3)不确定是否发生,用“可能”表示。
这就是事物发生的可能性。
可能性
【例1】在括号里填上“一定”“可能”或“不可能”。
(1)强强比兵兵大3岁,但是强强身高却比兵兵矮2厘米。( )
这句话描述的是两个人年龄和身高的比较情况,是一个客观事实。强强比兵兵大3岁,但是身高却比兵兵矮2厘米,这件事可能发生。
可能
【例1】在括号里填上“一定”“可能”或“不可能”。
(2)在标有1~20的十张卡片中随意摸出2张卡片,两张卡片的和是40。( )
从1到10中,两个最大的数19和20的和是39,不可能出现和为40,所以在标有1~20的十张卡片中随意摸出2张卡片,两张卡片的和不可能是40。
不可能
【例1】在括号里填上“一定”“可能”或“不可能”。
(3)铁和木头都能浮在水面上。( )
铁的密度大于水,通常情况下铁会下沉,而木头有可能浮在水面上,所以这句话是不可能的。
不可能
【例2】把5个红球和3个黄球放在同一个盒子里,任意摸出一个球,( )是白色的。
A.一定 B.可能 C.不可能
因为盒子里只有红球和黄球,根本没有白球,所以不可能摸出白球。
C
【例3】下面的事件一定会发生的是( )。
A. 下个月会下雪
B. 明天太阳会从东方升起
C. 掷骰子掷出7点
A选项下个月是否会下雪具有不确定性,不是一定会发生;
B选项太阳每天都会从东方升起,这是自然规律,是一定会发生的;
C选项骰子只有1到6点,不可能掷出7点。所以一定发生的是B选项。
B
【例4】下面说法正确的是( )。
A. 小王掷骰子,连续5次都是六点,如果再掷一次,那么肯定是六点。
B. 每天都一定有24个小时。
C. 天上出现乌云,意味着肯定要下雨了。
A选项,每次掷骰子的结果都是独立的、随机的,之前连续5次六点,下一次仍有可能是六点,但不是肯定是六点,A选项错误;
B选项,一天就是24个小时,这是确定的,B选项正确;
C选项,天上出现乌云只是有可能下雨,不是肯定要下雨,C选项错误。
B
事件发生的可能性是有大小的。
事件随机出现的可能性的大小与个体数量的多少有关。
个体在总数量中所占数量越多,出现的可能性就越大;
反之,可能性就越小。
可能性的大小
【例5】从1~4四张数字卡片中依次抽出两张,所得数字之和是( )的可能性最大。
从 1、2、3、4中依次抽出两张,所有可能的情况有:1和2、1和3、1和4、2和3、2和4、3和4,它们的和分别是3、4、5、5、6、7其中和为5的情况有2种,出现的次数最多,所以所得数字之和是5的可能性最大。
5
【例6】盒子里有红、白、蓝三种颜色的小球共 25 个,它们除颜色外都相同。任意摸一个球,要使摸到红球的可能性最小,那么盒中最多有( )个红球。
要使摸到红球的可能性最小,红球数量应最少,让白球和蓝球数量尽量多且接近,25÷3=8……1,即平均每种颜色8个还余1个,把余下的1个给白球或蓝球,那么白球和蓝球各9个,红球最多7个。
7
【例7】盒子里有8个球,除颜色外完全相同,在( )条件下,摸出黑球的可能性大。
A.5黑3白 B.2黑6白 C.3黑5白
要摸出黑球可能性大,黑球数量要多于白球数量。
A选项黑球5个多于白球3个,满足条件;
B选项黑球2个少于白球6个,不符合;
C选项黑球3个少于白球5个,不符合。所以答案选A。
A
【例8】从三张分别写有5、7和9数字的纸中任意抽出两张,它们的差是( )的可能性最大。
从 5、7、9 中任意抽出两张,会出现5和7、5和9、7和9三种情况,它们的差分别是:7-5=2,9-5=4,9-7=2,差是2出现了两次,所以差是2的可能性最大。
2
【例9】下面每个盒子里都有 10 个大小相同的球,一定可以摸出蓝球的是( )。
A.8个红球,2个蓝球 B.10个黄球 C.10个蓝球
要想一定摸出某种颜色的球,那么盒子中必须全部都是这种颜色的球。选项A中既有红球又有蓝球,不一定能摸出蓝球;选项B中都是黄球,不可能摸出蓝球;选项C中全是蓝球,所以一定可以摸出蓝球。
C
【例10】从 3,4,5三张数卡中任抽两张,组成一个两位数,如果组成的是质数则兵兵赢,组成的是合数则贝贝赢,这个游戏规则公平吗?
从3,4,5三张数卡中任抽两张组成两位数有34、35、43、45、53、54共6个。其中质数有43,53共2个;合数有34,35,45,54共4个,抽到质数和合数的可能性不同,所以这个游戏规则不公平。
【例11】甲、乙两人轮流掷小正方体,约定红面朝上算甲赢1分,黄面朝上算乙赢1分。用下面( )的小正方体掷是最公平的。
A. 3红3黄 B. 4红2黄 C. 2红4黄 D. 1红5黄
公平的关键在于红面和黄面出现的概率相同,即红面和黄面的数量要相同。
A选项红面和黄面都有3个,数量相等,公平;
B选项红面4个,黄面2个,数量不同,不公平;
C选项红面2个,黄面4个,数量不同,不公平;
D选项红面1个,黄面5个,数量不同,不公平。所以选A。
A
【例12】奇奇和亮亮用摸球游戏来决定谁先开始打篮球,摸到黄球小明先开始,摸到蓝球小亮先开始,在下面( )盒子中摸最公平。A.黄球8个,蓝球2个
B.黄球5个,蓝球5个
C.黄球3个,蓝球7个
要使游戏公平,那么盒子中两种颜色球的数量应该相等。
A选项黄球比蓝球多很多,不公平;
C选项蓝球比黄球多很多,不公平;
只有B选项黄球和蓝球数量相等,是公平的。
B
可能情况的个数
为了不重复、不遗漏地列出所有可能出现的结果,可以借助树状图或列表等方法找出事件所有可能出现的结果;再根据每种结果出现的次数,判断哪种结果出现的可能性最大。
【例13】盒子里有3个红球,2个蓝球(球除颜色外完全相同),一次摸出两个球,可能有( )种结果。
一次摸两个球,可能出现的情况有:两个红球、两个蓝球、一个红球和一个蓝球,共3种情况。
3
【例14】从标有数字1、2、3、4的四张牌中任意抽 2张,可以组成( )个不同两位数。
当抽中1和2时,可以组成12和21;
当抽中1和3时,可以组成13和31;
当抽中1和4时,可以组成14和41;
当抽中2和3时,可以组成23和32;
当抽中2和4时,可以组成24和42;
当抽中3和4时,可以组成34和43,共12个不同的两位数。
12
【例15】从红、黄、蓝、绿、白五种颜色中选出两种,有多少种不同的选法?
从五种颜色中选两种,可以用列举法。
先选红色,那么可以和黄、蓝、绿、白分别组合,有4种选法;
再选黄色,因为和红色已经组合过了,所以可以和蓝、绿、白组合,有3种选法;
接着选蓝色,和绿、白组合,有2种选法;
然后选绿色,和白组合,有1种选法。
将所有选法相加:4+3+2+1=10(种)。
1、甲、乙和小丙三人在玩“石头、剪刀、布”的游戏,下面说法正确的是( )。
A.甲可能赢
B.乙一定赢
C.丙一定输
A
2、盒子中有3张20元和2张50元纸币,从盒子中任意摸出两张,下面说法正确的是( )。
A. 总钱数一定是70元
B. 总钱数可能是40元
C. 总钱数不可能是100元
D. 总钱数可能是120元
B
3、一个盒子装有大小形状完全相同的黑球4个,绿球5个,紫球3个,摸到黑球鸣鸣赢,摸到绿球港港赢,为使游戏公平,盒子中应( )。
A.加入1个黑球
B.加入2个紫球
C.加入1个绿球
D.拿出3个紫球
A
每一份努力,都将在学习中得到最好的回报。加油!
