第六单元_第18课时_ 数学思考(二) (教学课件)-六年级数学下册人教版(共31张PPT)
文档属性
| 名称 | 第六单元_第18课时_ 数学思考(二) (教学课件)-六年级数学下册人教版(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 20:45:21 | ||
图片预览











文档简介
(共31张PPT)
小学数学·六年级(下)·RJ
第18课时 总复习 数学思考(二)
经历用推理解决问题的过程,进一步提升推理能力和解决问题的能力。
掌握运用等量代换和等式的性质进行推理的方法,会用此方法解决一些简单的实际问题。
在教学活动中,学会用数学思想方法解决问题,有条理地表达自己思考的过程,培养合作意识。
掌握运用等量代换和等式的性质进行推理的方法,会用此方法解决一些简单的实际问题。
数学思考(二)
、 、 、 、 各代表一个数。
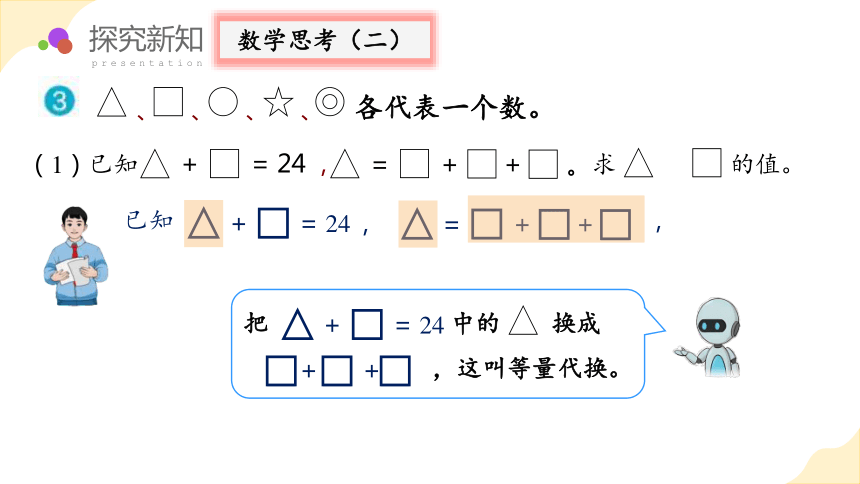
(1)已知
+ = 24 ,
= + + 。求 和 的值。
用自己的方式尝试解决这个问题,做完后在小组内交流,交流时把思路讲清楚,并相互补充。
数学思考(二)
、 、 、 、 各代表一个数。
(1)已知
+ = 24 ,
= + + 。求 和 的值。
= + +
已知 ,
+ = 24 ,
把 中的 换成
,这叫等量代换。
+ = 24
+ +
数学思考(二)
、 、 、 、 各代表一个数。
(1)已知
+ = 24 ,
= + + 。求 和 的值。
= + +
已知 ,
+ = 24 ,
可得 ,
所以
= 6 。
= + + =18。
+ + + =24 即
4× = 24 ,
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
独立思考:①想一想, 是否等于 ?为什么?
②在问题解决的过程中,每一步的依据是什么?
小组交流:在小组内说说自己的结论,把理由说清楚,并相互补充。如果存在意见不统一的地方,在小组内讨论、处理。
+ =160
+ =160
=160 -
-
+
=160 -
+
-
=160 -
=160 -
=
等式的性质
等式的性质
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
=160 - 。
+ =160,
+ =160,
已知
根据等式的性质,等式两边都减去 。
=160 - ,
可以推出
= 。
因为 代表一个数,所以
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
+ =160,
已知
根据等式的性质,等式两边都减去160。
= 。
所以
所以 =160- ,
可得 +160- =160。
可得
- =0。
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
+ =160,
+ =160,
因为
根据等式的性质,等式两边都减去 。
= 。
由此推出
+ =
+ 。
所以
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
等式的性质
等量代换
经历用推理解决问题的过程,进一步提升推理能力和解决问题的能力。
1.不测量,你能说出下面哪些角的度数?
( )
( )
( )
( )
180°
90°
什么是平角?平角与直线有什么区别?
一条射线绕它的端点旋转,当始边和终边在同一条直线上,方向相反时,所构成的角叫平角。平角是一个特殊的角,1平角=180°。
直线没有端点,不可度量;
平角有两条边和一个顶点,可度量。
如图,两条直线相交于点O。
2
1
4
3
O
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
∠1 和∠2
∠1 和∠4
能组成4个平角
∠3 和∠4
∠2 和∠3
(2)你能推出∠1=∠3吗?
什么是平角?平角与直线有什么区别?
如图,两条直线相交于点O。
2
1
4
3
O
你能推出∠1=∠3吗?
2
1
4
3
O
(2)你能推出∠1=∠3吗?
∠1+∠2=180°
∠2+∠3=180°
∠1=∠3
∠1=180°-∠2
∠3=180°-∠2
∠1+∠2-∠2=180°-∠2
∠2+∠3-∠2=180°-∠2
方法一
如图,两条直线相交于点O。
2
1
4
3
O
(2)你能推出∠1=∠3吗?
∠1+∠4=180°
∠3+∠4=180°
∠1=∠3
∠1 =180°-∠4
∠3 =180°-∠4
∠1+∠4-∠4=180°-∠4
∠3+∠4-∠4=180°-∠4
方法二
如图,两条直线相交于点O。
(2)你能推出∠1=∠3吗?
等式的性质
2
1
4
3
O
如图,两条直线相交于点O。
(2)你能推出∠1=∠3吗?
∠1+∠2=180°,
∠2+∠3=180°。
因为180°-∠2=180°-∠2,所以∠1=∠3。
可以得到∠1=180°-∠2,∠3=180°-∠2。
根据等式的性质,等式两边都减去∠2,
方法一
2
1
4
3
O
如图,两条直线相交于点O。
(2)你能推出∠1=∠3吗?
∠1+∠4=180°,
∠3+∠4=180°。
因为180°-∠4=180°-∠4,所以∠1=∠3。
可以得到∠1=180°-∠4,∠3=180°-∠4。
根据等式的性质,等式两边都减去∠4,
方法二
2
1
4
3
O
如图,两条直线相交于点O。
你能用同样的方法推出∠2=∠4吗?
∠2+∠3=180°,
∠4+∠3=180°。
因为180°-∠3=180°-∠3,所以∠2=∠4。
可以得到∠2=180°-∠3,∠4=180°-∠3。
根据等式的性质,等式两边都减去∠3,
方法一
2
1
4
3
O
如图,两条直线相交于点O。
你能用同样的方法推出∠2=∠4吗?
∠2+∠1=180°,
∠4+∠1=180°。
因为180°-∠1=180°-∠1,所以∠2=∠4。
可以得到∠2=180°-∠1,∠4=180°-∠1。
根据等式的性质,等式两边都减去∠1,
方法二
2
1
4
3
O
如图,两条直线相交于点O。
达标练习,巩固成果
○+□=91
△+□=63
△+○=46
1. ○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
△
△
○
○
□
□
根据等式的性质,将三个等式的两边分别相加,
可得,2×○+2×□+2×△=91+63+46,
即2×(○+□+△)=200,求得○+□+△=100。
由④式减①式可得,△=100-91=9。
由④式减②式可得,○=100-63=37。
方法一:
①
②
③
由④式减③式可得,□=100-46=54。
④
○+□=91
△+□=63
△+○=46
1. ○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
□
□
根据等式的性质,由①式减②式可得,
即○-△=28。
根据等式的性质,由③式加④式可得,
方法二:
由①式得,37+□=91,求得□=54。
由③式得,△+37=46,求得△=9。
①
②
△+○+(○-△)=46+28,
④
○+□-(△+□)=91-63,
③
即2×○=74,求得○=37。
2.○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
(1)○ + □ = 91
△ + □ = 63
△ + ○ = 46
(2)□ - ○ =8
□ + ○ =12
△= □ + □ + ○
□=54,○=37,△=9
□=10,○=2,△=22
3.如图,把三角形ABC的边BC延长到点D。
(1) ∠3 和 ∠4 拼成的是什么角?
1
2
3
4
A
B
C
D
(2) 你能说明 ∠1 + ∠2 = ∠4 吗?
答:∠3 与 ∠4 可以拼成一个平角。
如图可得 ∠3 + ∠4 =180°,
∠1 + ∠2 + ∠3 = 180° 。
可得 ∠4 = 180° - ∠3,∠1 + ∠2 = 180° - ∠3 。
因为 180° - ∠3 = 180° - ∠3 。
所以 ∠1 + ∠2 = ∠4 。
4.如图,四边形ABCD是一个平行四边形,图中
S阴影部分和S空白部分相等吗?
S阴影部分=S△AEF+S△DEG
= ×BF×h+ ×FG×h+ ×CG×h
= ×AD×h
∴ ×AD×h= ×BC×h。
= ×AE×h+ ×DE×h
∴S阴影部分=S空白部分。
h
h
h
h
∵AD=BC,
S空白部分=S△ABF+S△EFG+S△CDG
= ×(AE+DE)×h
= ×(BF+FG+CG)×h
= ×BC×h
5.如图所示,已知∠1=∠2,∠3=∠4,求∠5的度数。
【答案】∠1+∠2+∠3+∠4=180°-70°=110°
因为∠1=∠2,∠3=∠4,所以∠2+∠4=110°÷2=55°。
∠2+∠4+∠5=180°
∠5=180°-∠2-∠4=180°-55°=125°
答:∠5的度数是125°。
小学数学·六年级(下)·RJ
第18课时 总复习 数学思考(二)
经历用推理解决问题的过程,进一步提升推理能力和解决问题的能力。
掌握运用等量代换和等式的性质进行推理的方法,会用此方法解决一些简单的实际问题。
在教学活动中,学会用数学思想方法解决问题,有条理地表达自己思考的过程,培养合作意识。
掌握运用等量代换和等式的性质进行推理的方法,会用此方法解决一些简单的实际问题。
数学思考(二)
、 、 、 、 各代表一个数。
(1)已知
+ = 24 ,
= + + 。求 和 的值。
用自己的方式尝试解决这个问题,做完后在小组内交流,交流时把思路讲清楚,并相互补充。
数学思考(二)
、 、 、 、 各代表一个数。
(1)已知
+ = 24 ,
= + + 。求 和 的值。
= + +
已知 ,
+ = 24 ,
把 中的 换成
,这叫等量代换。
+ = 24
+ +
数学思考(二)
、 、 、 、 各代表一个数。
(1)已知
+ = 24 ,
= + + 。求 和 的值。
= + +
已知 ,
+ = 24 ,
可得 ,
所以
= 6 。
= + + =18。
+ + + =24 即
4× = 24 ,
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
独立思考:①想一想, 是否等于 ?为什么?
②在问题解决的过程中,每一步的依据是什么?
小组交流:在小组内说说自己的结论,把理由说清楚,并相互补充。如果存在意见不统一的地方,在小组内讨论、处理。
+ =160
+ =160
=160 -
-
+
=160 -
+
-
=160 -
=160 -
=
等式的性质
等式的性质
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
=160 - 。
+ =160,
+ =160,
已知
根据等式的性质,等式两边都减去 。
=160 - ,
可以推出
= 。
因为 代表一个数,所以
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
+ =160,
已知
根据等式的性质,等式两边都减去160。
= 。
所以
所以 =160- ,
可得 +160- =160。
可得
- =0。
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
+ =160,
+ =160,
因为
根据等式的性质,等式两边都减去 。
= 。
由此推出
+ =
+ 。
所以
、 、 、 、 各代表一个数。
(2)已知 + =160, + =160。 是否等于 ?
等式的性质
等量代换
经历用推理解决问题的过程,进一步提升推理能力和解决问题的能力。
1.不测量,你能说出下面哪些角的度数?
( )
( )
( )
( )
180°
90°
什么是平角?平角与直线有什么区别?
一条射线绕它的端点旋转,当始边和终边在同一条直线上,方向相反时,所构成的角叫平角。平角是一个特殊的角,1平角=180°。
直线没有端点,不可度量;
平角有两条边和一个顶点,可度量。
如图,两条直线相交于点O。
2
1
4
3
O
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
∠1 和∠2
∠1 和∠4
能组成4个平角
∠3 和∠4
∠2 和∠3
(2)你能推出∠1=∠3吗?
什么是平角?平角与直线有什么区别?
如图,两条直线相交于点O。
2
1
4
3
O
你能推出∠1=∠3吗?
2
1
4
3
O
(2)你能推出∠1=∠3吗?
∠1+∠2=180°
∠2+∠3=180°
∠1=∠3
∠1=180°-∠2
∠3=180°-∠2
∠1+∠2-∠2=180°-∠2
∠2+∠3-∠2=180°-∠2
方法一
如图,两条直线相交于点O。
2
1
4
3
O
(2)你能推出∠1=∠3吗?
∠1+∠4=180°
∠3+∠4=180°
∠1=∠3
∠1 =180°-∠4
∠3 =180°-∠4
∠1+∠4-∠4=180°-∠4
∠3+∠4-∠4=180°-∠4
方法二
如图,两条直线相交于点O。
(2)你能推出∠1=∠3吗?
等式的性质
2
1
4
3
O
如图,两条直线相交于点O。
(2)你能推出∠1=∠3吗?
∠1+∠2=180°,
∠2+∠3=180°。
因为180°-∠2=180°-∠2,所以∠1=∠3。
可以得到∠1=180°-∠2,∠3=180°-∠2。
根据等式的性质,等式两边都减去∠2,
方法一
2
1
4
3
O
如图,两条直线相交于点O。
(2)你能推出∠1=∠3吗?
∠1+∠4=180°,
∠3+∠4=180°。
因为180°-∠4=180°-∠4,所以∠1=∠3。
可以得到∠1=180°-∠4,∠3=180°-∠4。
根据等式的性质,等式两边都减去∠4,
方法二
2
1
4
3
O
如图,两条直线相交于点O。
你能用同样的方法推出∠2=∠4吗?
∠2+∠3=180°,
∠4+∠3=180°。
因为180°-∠3=180°-∠3,所以∠2=∠4。
可以得到∠2=180°-∠3,∠4=180°-∠3。
根据等式的性质,等式两边都减去∠3,
方法一
2
1
4
3
O
如图,两条直线相交于点O。
你能用同样的方法推出∠2=∠4吗?
∠2+∠1=180°,
∠4+∠1=180°。
因为180°-∠1=180°-∠1,所以∠2=∠4。
可以得到∠2=180°-∠1,∠4=180°-∠1。
根据等式的性质,等式两边都减去∠1,
方法二
2
1
4
3
O
如图,两条直线相交于点O。
达标练习,巩固成果
○+□=91
△+□=63
△+○=46
1. ○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
△
△
○
○
□
□
根据等式的性质,将三个等式的两边分别相加,
可得,2×○+2×□+2×△=91+63+46,
即2×(○+□+△)=200,求得○+□+△=100。
由④式减①式可得,△=100-91=9。
由④式减②式可得,○=100-63=37。
方法一:
①
②
③
由④式减③式可得,□=100-46=54。
④
○+□=91
△+□=63
△+○=46
1. ○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
□
□
根据等式的性质,由①式减②式可得,
即○-△=28。
根据等式的性质,由③式加④式可得,
方法二:
由①式得,37+□=91,求得□=54。
由③式得,△+37=46,求得△=9。
①
②
△+○+(○-△)=46+28,
④
○+□-(△+□)=91-63,
③
即2×○=74,求得○=37。
2.○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
(1)○ + □ = 91
△ + □ = 63
△ + ○ = 46
(2)□ - ○ =8
□ + ○ =12
△= □ + □ + ○
□=54,○=37,△=9
□=10,○=2,△=22
3.如图,把三角形ABC的边BC延长到点D。
(1) ∠3 和 ∠4 拼成的是什么角?
1
2
3
4
A
B
C
D
(2) 你能说明 ∠1 + ∠2 = ∠4 吗?
答:∠3 与 ∠4 可以拼成一个平角。
如图可得 ∠3 + ∠4 =180°,
∠1 + ∠2 + ∠3 = 180° 。
可得 ∠4 = 180° - ∠3,∠1 + ∠2 = 180° - ∠3 。
因为 180° - ∠3 = 180° - ∠3 。
所以 ∠1 + ∠2 = ∠4 。
4.如图,四边形ABCD是一个平行四边形,图中
S阴影部分和S空白部分相等吗?
S阴影部分=S△AEF+S△DEG
= ×BF×h+ ×FG×h+ ×CG×h
= ×AD×h
∴ ×AD×h= ×BC×h。
= ×AE×h+ ×DE×h
∴S阴影部分=S空白部分。
h
h
h
h
∵AD=BC,
S空白部分=S△ABF+S△EFG+S△CDG
= ×(AE+DE)×h
= ×(BF+FG+CG)×h
= ×BC×h
5.如图所示,已知∠1=∠2,∠3=∠4,求∠5的度数。
【答案】∠1+∠2+∠3+∠4=180°-70°=110°
因为∠1=∠2,∠3=∠4,所以∠2+∠4=110°÷2=55°。
∠2+∠4+∠5=180°
∠5=180°-∠2-∠4=180°-55°=125°
答:∠5的度数是125°。
