18.2.2 菱形的性质和判定 同步练习(无答案)2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 18.2.2 菱形的性质和判定 同步练习(无答案)2023-2024学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 158.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 09:41:36 | ||
图片预览

文档简介
菱形的性质和判定
一、填空题
1.在平面直角坐标系xOy中,菱形ABCD的四个顶点都在坐标轴上.若A(-4,0),B(0,-3),则菱形ABCD的面积是________.
2.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到点E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF=,则BD的长为________(结果保留根号).
3.菱形ABCD的边长为1,面积为,则AC-BD(AC>BD)的值是________.
4.如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是_______________________.(只需写出一个条件即可)
5.如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是______________________.(写出一个即可)
6.如图,在四边形ABCD中,E,F分别是线段AD,BC的中点,G,H分别是线段BD,AC的中点,当四边形ABCD的边满足________时,四边形EGFH是菱形.
二、选择题
1.如图,在菱形ABCD中,对角线AC,BD相交于点O,E为CD的中点.若OE=3,则菱形ABCD的周长为( )
A.6 B.12 C.24 D.48
2.如图,在菱形ABCD中,AB=5,对角线AC=8,则AB边上的高DE等于( )
A.9.6 B.4.8 C.5 D.2.4
3.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,A,B两点的坐标分别是(2,2),(-1,-),点D在第一象限,则点D的坐标是( )
A.(6,2) B.(8,2) C.(6,) D.(8,)
4.如图,在菱形ABCD中,对角线AC,BD相交于点O,E,F分别是AB,AO的中点,连接EF,BF.若AF=1,
AE=,则FB的长为( )
A.3 B.2 C. D.3
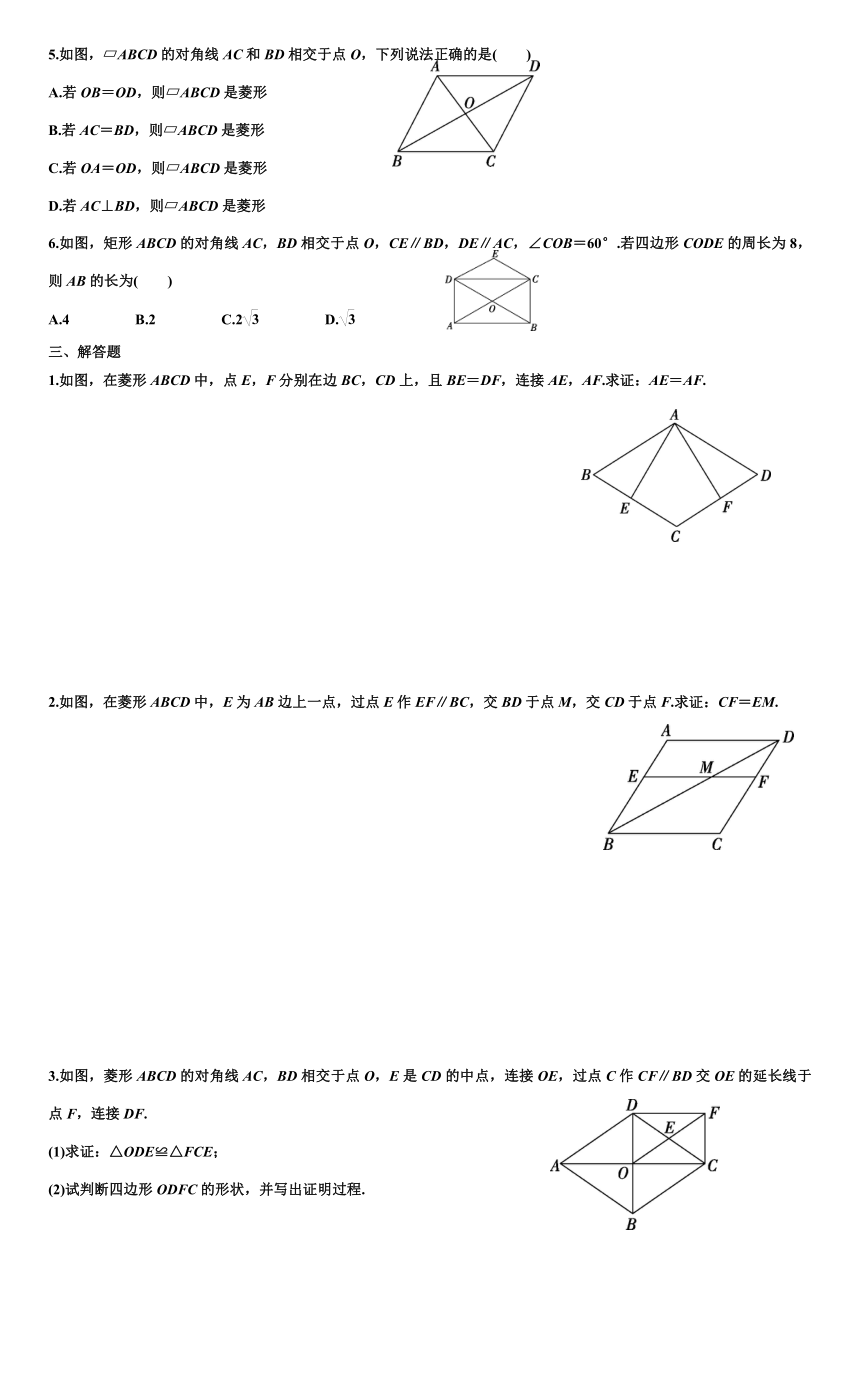
5.如图, ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
A.若OB=OD,则 ABCD是菱形
B.若AC=BD,则 ABCD是菱形
C.若OA=OD,则 ABCD是菱形
D.若AC⊥BD,则 ABCD是菱形
6.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC,∠COB=60°.若四边形CODE的周长为8,则AB的长为( )
A.4 B.2 C.2 D.
解答题
1.如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连接AE,AF.求证:AE=AF.
2.如图,在菱形ABCD中,E为AB边上一点,过点E作EF∥BC,交BD于点M,交CD于点F.求证:CF=EM.
3.如图,菱形ABCD的对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交OE的延长线于点F,连接DF.
(1)求证:△ODE≌△FCE;
(2)试判断四边形ODFC的形状,并写出证明过程.
4.已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与线段CB,DC交于点E,F,且∠EAF=60°.
(1)如图①,当E是线段CB的中点时,写出线段AE,EF,AF之间的数量关系;
(2)如图②,当E是线段CB上任意一点时(不与点B,C重合),求证:BE=CF.
5.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AC=6,BD=8,过点A作AH⊥BC于点H,求AH的长.
6.如图,点E,F分别在 ABCD的边AB,BC上,AE=CF,连接DE,DF.请从以下三个条件:①∠1=∠2;②DE=DF;③∠3=∠4中,选择一个合适的作为已知条件,使 ABCD为菱形.
(1)你添加的条件是________(填序号);
(2)添加了条件后,请证明 ABCD为菱形.
7.如图,△ABC中,D是AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.
(1)求证:AD=CF;
(2)连接AF,CD.如果D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形,证明你的结论.
8.如图,在 ABCD中,AB=2,AD=1,∠ADC=60°,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若P是直线l上的一个动点,请计算PD′+PB的最小值.
一、填空题
1.在平面直角坐标系xOy中,菱形ABCD的四个顶点都在坐标轴上.若A(-4,0),B(0,-3),则菱形ABCD的面积是________.
2.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到点E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF=,则BD的长为________(结果保留根号).
3.菱形ABCD的边长为1,面积为,则AC-BD(AC>BD)的值是________.
4.如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是_______________________.(只需写出一个条件即可)
5.如图,将△ABC沿着BC方向平移得到△DEF,只需添加一个条件即可证明四边形ABED是菱形,这个条件可以是______________________.(写出一个即可)
6.如图,在四边形ABCD中,E,F分别是线段AD,BC的中点,G,H分别是线段BD,AC的中点,当四边形ABCD的边满足________时,四边形EGFH是菱形.
二、选择题
1.如图,在菱形ABCD中,对角线AC,BD相交于点O,E为CD的中点.若OE=3,则菱形ABCD的周长为( )
A.6 B.12 C.24 D.48
2.如图,在菱形ABCD中,AB=5,对角线AC=8,则AB边上的高DE等于( )
A.9.6 B.4.8 C.5 D.2.4
3.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,A,B两点的坐标分别是(2,2),(-1,-),点D在第一象限,则点D的坐标是( )
A.(6,2) B.(8,2) C.(6,) D.(8,)
4.如图,在菱形ABCD中,对角线AC,BD相交于点O,E,F分别是AB,AO的中点,连接EF,BF.若AF=1,
AE=,则FB的长为( )
A.3 B.2 C. D.3
5.如图, ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
A.若OB=OD,则 ABCD是菱形
B.若AC=BD,则 ABCD是菱形
C.若OA=OD,则 ABCD是菱形
D.若AC⊥BD,则 ABCD是菱形
6.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC,∠COB=60°.若四边形CODE的周长为8,则AB的长为( )
A.4 B.2 C.2 D.
解答题
1.如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连接AE,AF.求证:AE=AF.
2.如图,在菱形ABCD中,E为AB边上一点,过点E作EF∥BC,交BD于点M,交CD于点F.求证:CF=EM.
3.如图,菱形ABCD的对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交OE的延长线于点F,连接DF.
(1)求证:△ODE≌△FCE;
(2)试判断四边形ODFC的形状,并写出证明过程.
4.已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与线段CB,DC交于点E,F,且∠EAF=60°.
(1)如图①,当E是线段CB的中点时,写出线段AE,EF,AF之间的数量关系;
(2)如图②,当E是线段CB上任意一点时(不与点B,C重合),求证:BE=CF.
5.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AC=6,BD=8,过点A作AH⊥BC于点H,求AH的长.
6.如图,点E,F分别在 ABCD的边AB,BC上,AE=CF,连接DE,DF.请从以下三个条件:①∠1=∠2;②DE=DF;③∠3=∠4中,选择一个合适的作为已知条件,使 ABCD为菱形.
(1)你添加的条件是________(填序号);
(2)添加了条件后,请证明 ABCD为菱形.
7.如图,△ABC中,D是AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.
(1)求证:AD=CF;
(2)连接AF,CD.如果D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形,证明你的结论.
8.如图,在 ABCD中,AB=2,AD=1,∠ADC=60°,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若P是直线l上的一个动点,请计算PD′+PB的最小值.
