10.1.4 设计轴对称图案 同步练习(含答案)2023—2024学年华东师大版数学七年级下册
文档属性
| 名称 | 10.1.4 设计轴对称图案 同步练习(含答案)2023—2024学年华东师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 161.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 00:00:00 | ||
图片预览

文档简介
10.1.4 设计轴对称图案优选习题
一、单选题
1.如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
A. B. C. D.
2.如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是( )
A. B.6 C.4 D.5
3.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF的长为( )
A.10 B.12 C.13 D.6
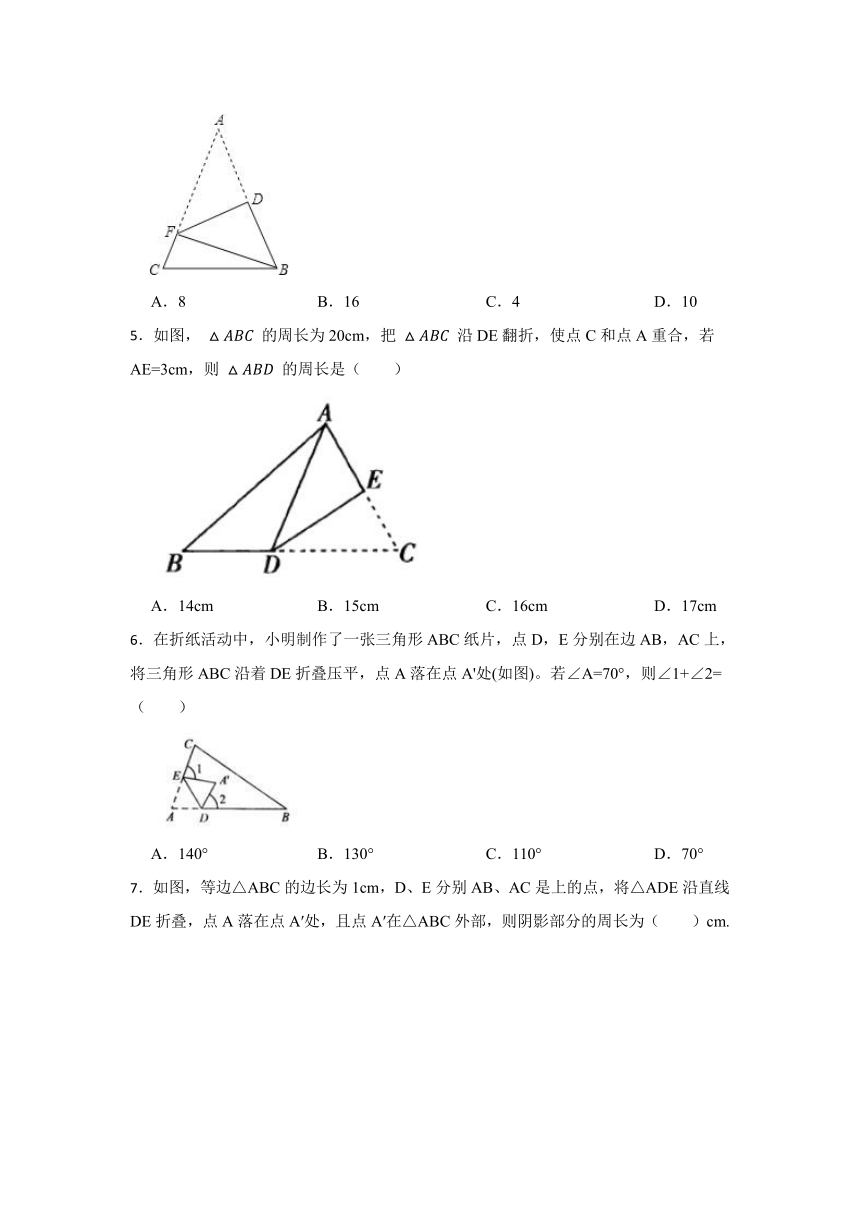
4.如图,在△ABC中,AB=AC,AB+BC=8.将△ABC折叠,使得点A落在点B处,折痕DF分别与AB、AC交于点D、F,连接BF,则△BCF的周长是( )
A.8 B.16 C.4 D.10
5.如图, 的周长为20cm,把 沿DE翻折,使点C和点A重合,若AE=3cm,则 的周长是( )
A.14cm B.15cm C.16cm D.17cm
6.在折纸活动中,小明制作了一张三角形ABC纸片,点D,E分别在边AB,AC上,将三角形ABC沿着DE折叠压平,点A落在点A'处(如图)。若∠A=70°,则∠1+∠2=( )
A.140° B.130° C.110° D.70°
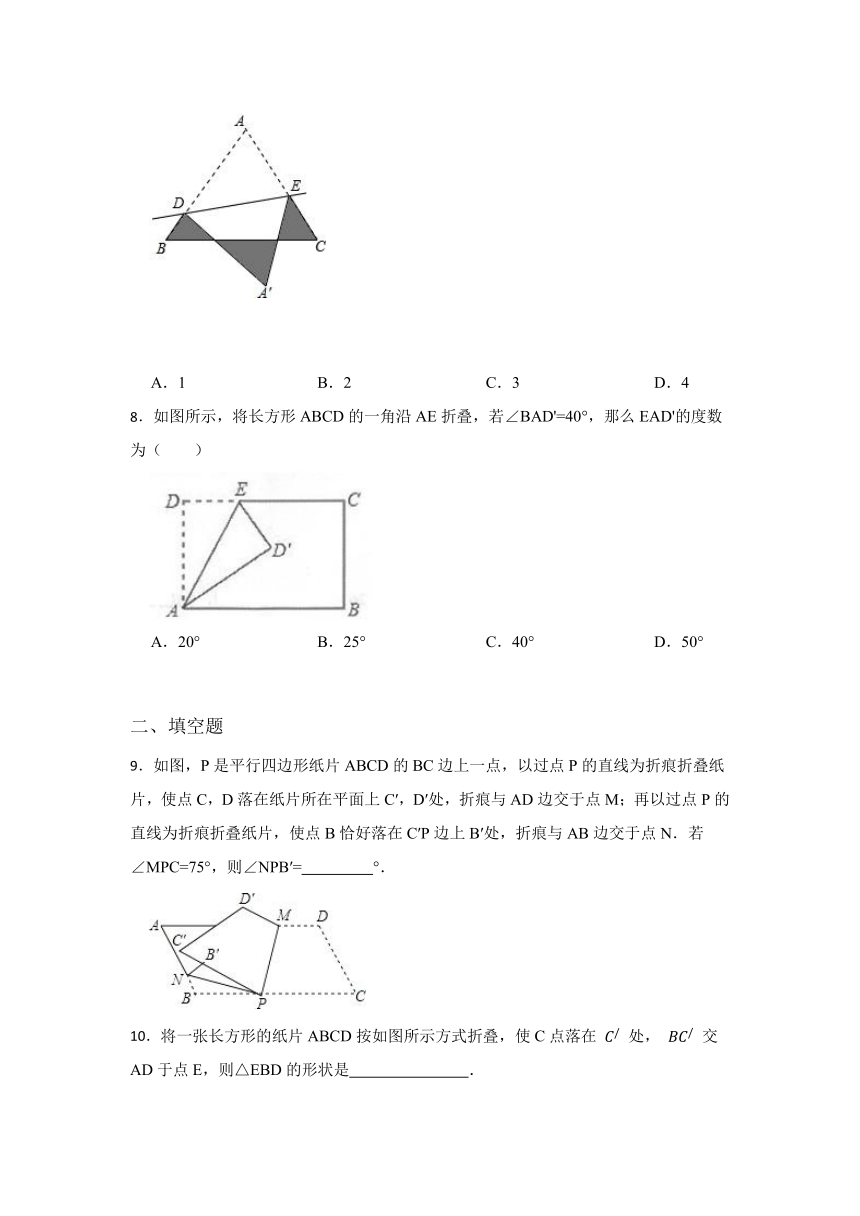
7.如图,等边△ABC的边长为1cm,D、E分别AB、AC是上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )cm.
A.1 B.2 C.3 D.4
8.如图所示,将长方形ABCD的一角沿AE折叠,若∠BAD'=40°,那么EAD'的度数为( )
A.20° B.25° C.40° D.50°
二、填空题
9.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′= °.
10.将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在 处, 交AD于点E,则△EBD的形状是 .
11.如图所示,把一张长方形纸片沿 折叠后,点 分别落在点 的位置.若 ,则 等于 .
12.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
13.如图,把一张宽度相等的纸条按图上所示的方式折叠,则∠1的度数等于 °.
14.如图,D、E、F是正△ABC各边上的点,沿EF折叠后A与D重合,BD<DC,则图中相等的角有 对.
三、解答题
15.如图,在长方形ABCD中,DC=9,在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若OABF的面积是54,求DE的长.
16.如图,将矩形沿EF折叠,使B1点落在边上的B点处;再将矩形沿BG折叠,使D1点落在D点处且BD过F点.
(1)求证:四边形BEFG是平行四边形;
(2)当是多少度时,四边形BEFG为菱形 试说明理由.
17.如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF= +1,求BC的长.
参考答案与试题解析
1.答案:C
2.答案:B
3.答案:D
4.答案:A
5.答案:A
6.答案:A
7.答案:C
8.答案:B
9.答案:15
10.答案:等腰三角形
11.答案:50°
12.答案:3
13.答案:65°
14.答案:7
15.答案:解:因为 AB·BF=54,DC=AB=9,
所以BF= 12.
所以AF2=92+122=225,∴AF=15. .
所以BC=AD=AF=15,
所以CF= BC-BF=15-12=3.
设DE=x,则CE=9-x , EF=DE=x.
则x2=(9-x)2+32,
所以x=5.
所以DE的长为5.
16.答案:解;(1)∵A1D1∥B1C1,
∴∠B1FE=∠FEB.
又∵∠B1FE=∠BFE,
∴∠FEB=∠BFE.
∴BE=BF.
同理可得:FG=BF.
∴BE=FG,
又∵BE∥FG,
∴四边形BEFG是平行四边形;
(2)当∠B1FE=60°时,四边形EFGB为菱形.
理由如下:
∵∠B1FE=60°,
∴∠BFE=∠BEF=60°,
∴△BEF为等边三角形,即BE=EF.
∵四边形BEFG是平行四边形,BE=EF.
∴四边形BEFG是菱形(一组邻边相等的平行四边形是菱形).
17.答案:解:由题意,得:∠3=180°﹣2∠1=45°,∠4=180°﹣2∠2=30°,BE=KE、KF=FC,如图,过点K作KM⊥BC于点M,设KM=x,则EM=x、MF= x,∴x+ x= +1,解得:x=1,∴EK= 、KF=2,∴BC=BE+EF+FC=EK+EF+KF=3+ + ,∴BC的长为3+ +
一、单选题
1.如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
A. B. C. D.
2.如图,在矩形纸片 中, ,点 在边 上,将 沿直线 折叠,点 恰好落在对角线 上的点 处,若 ,则 的长是( )
A. B.6 C.4 D.5
3.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF的长为( )
A.10 B.12 C.13 D.6
4.如图,在△ABC中,AB=AC,AB+BC=8.将△ABC折叠,使得点A落在点B处,折痕DF分别与AB、AC交于点D、F,连接BF,则△BCF的周长是( )
A.8 B.16 C.4 D.10
5.如图, 的周长为20cm,把 沿DE翻折,使点C和点A重合,若AE=3cm,则 的周长是( )
A.14cm B.15cm C.16cm D.17cm
6.在折纸活动中,小明制作了一张三角形ABC纸片,点D,E分别在边AB,AC上,将三角形ABC沿着DE折叠压平,点A落在点A'处(如图)。若∠A=70°,则∠1+∠2=( )
A.140° B.130° C.110° D.70°
7.如图,等边△ABC的边长为1cm,D、E分别AB、AC是上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )cm.
A.1 B.2 C.3 D.4
8.如图所示,将长方形ABCD的一角沿AE折叠,若∠BAD'=40°,那么EAD'的度数为( )
A.20° B.25° C.40° D.50°
二、填空题
9.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′= °.
10.将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在 处, 交AD于点E,则△EBD的形状是 .
11.如图所示,把一张长方形纸片沿 折叠后,点 分别落在点 的位置.若 ,则 等于 .
12.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
13.如图,把一张宽度相等的纸条按图上所示的方式折叠,则∠1的度数等于 °.
14.如图,D、E、F是正△ABC各边上的点,沿EF折叠后A与D重合,BD<DC,则图中相等的角有 对.
三、解答题
15.如图,在长方形ABCD中,DC=9,在DC上找一点E,沿直线AE把△AED折叠,使D点恰好落在BC上,设这一点为F,若OABF的面积是54,求DE的长.
16.如图,将矩形沿EF折叠,使B1点落在边上的B点处;再将矩形沿BG折叠,使D1点落在D点处且BD过F点.
(1)求证:四边形BEFG是平行四边形;
(2)当是多少度时,四边形BEFG为菱形 试说明理由.
17.如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF= +1,求BC的长.
参考答案与试题解析
1.答案:C
2.答案:B
3.答案:D
4.答案:A
5.答案:A
6.答案:A
7.答案:C
8.答案:B
9.答案:15
10.答案:等腰三角形
11.答案:50°
12.答案:3
13.答案:65°
14.答案:7
15.答案:解:因为 AB·BF=54,DC=AB=9,
所以BF= 12.
所以AF2=92+122=225,∴AF=15. .
所以BC=AD=AF=15,
所以CF= BC-BF=15-12=3.
设DE=x,则CE=9-x , EF=DE=x.
则x2=(9-x)2+32,
所以x=5.
所以DE的长为5.
16.答案:解;(1)∵A1D1∥B1C1,
∴∠B1FE=∠FEB.
又∵∠B1FE=∠BFE,
∴∠FEB=∠BFE.
∴BE=BF.
同理可得:FG=BF.
∴BE=FG,
又∵BE∥FG,
∴四边形BEFG是平行四边形;
(2)当∠B1FE=60°时,四边形EFGB为菱形.
理由如下:
∵∠B1FE=60°,
∴∠BFE=∠BEF=60°,
∴△BEF为等边三角形,即BE=EF.
∵四边形BEFG是平行四边形,BE=EF.
∴四边形BEFG是菱形(一组邻边相等的平行四边形是菱形).
17.答案:解:由题意,得:∠3=180°﹣2∠1=45°,∠4=180°﹣2∠2=30°,BE=KE、KF=FC,如图,过点K作KM⊥BC于点M,设KM=x,则EM=x、MF= x,∴x+ x= +1,解得:x=1,∴EK= 、KF=2,∴BC=BE+EF+FC=EK+EF+KF=3+ + ,∴BC的长为3+ +
