10.3.2 旋转的特征 同步练习(含答案)2023—2024学年华东师大版数学七年级下册
文档属性
| 名称 | 10.3.2 旋转的特征 同步练习(含答案)2023—2024学年华东师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 130.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 10:39:36 | ||
图片预览



文档简介
10.3.2 旋转的特征同步练习
一、单选题
1.如图,在△ABC中,∠BAC=55°,∠C=20°,将△ABC绕点A逆时针旋转α角度(0 α 180°)得到△ADE,若DE AB,则α的值为( )
A.65° B.75° C.85° D.130°
2.如图, 绕点 逆时针旋转90°到 的位置,已知 ,则 的度数为( )
A.55° B.35° C.40° D.45°
3.如图,香港特别行政区区徽中的紫荆花图案,该图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )
A.45° B.60° C.72° D.108°
4.对于平面图形上的任意两点P,Q,如果经过某种变换得到的新图形上的对应点P1,Q1,下列变换中不一定保证PQ=P1Q1的是( )
A.平移 B.旋转 C.翻折 D.位似
5.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
A.70° B.65° C.60° D.55°
6.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.逆时针旋转90° B.顺时针旋转90°
C.逆时针旋转45° D.顺时针旋转45°
7.如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是( )
A.∠AOC B.∠AOD C.∠AOB D.∠BOC
8.如图△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A.2 B. C.3 D.2
二、填空题
9.如图,△ABC≌△ADE,∠C与∠AED都是直角,点E在AB上,∠D=30°,那么△ABC绕着点 逆时针方向旋转 度能与△ADE重合.
10.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.
11.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为 .
12.如图,香港特别行政区区徽由五个相同的花瓣组成,它是以一个花瓣为基本图案通过连续四次旋转所组成,这四次旋转中,旋转角度最小是 °.
13.如图,点D是等腰 的底边AB上的点,若 且 ,将 绕点C逆时针旋转,使它与 重合,则 度
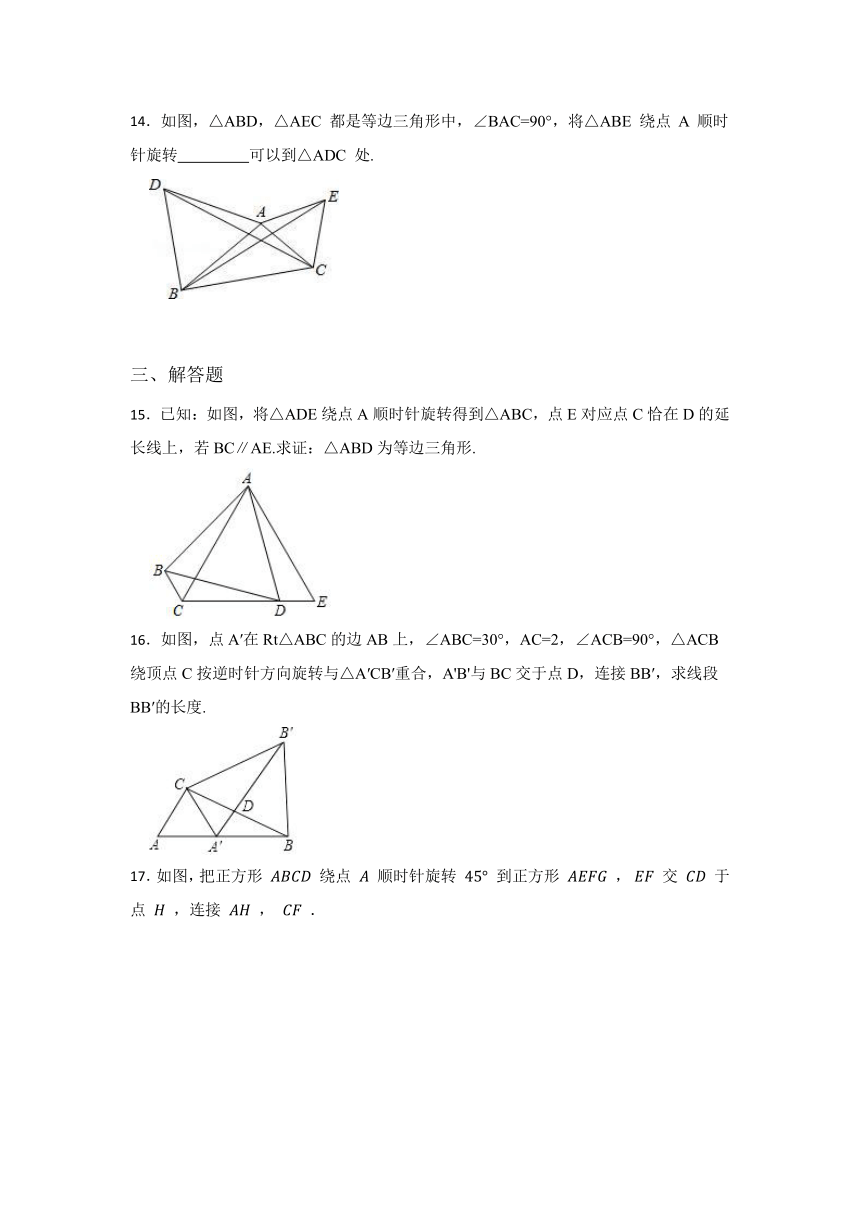
14.如图,△ABD,△AEC 都是等边三角形中,∠BAC=90°,将△ABE 绕点 A 顺时针旋转 可以到△ADC 处.
三、解答题
15.已知:如图,将△ADE绕点A顺时针旋转得到△ABC,点E对应点C恰在D的延长线上,若BC∥AE.求证:△ABD为等边三角形.
16.如图,点A′在Rt△ABC的边AB上,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,A'B'与BC交于点D,连接BB′,求线段BB′的长度.
17.如图,把正方形 绕点 顺时针旋转 到正方形 , 交 于点 ,连接 , .
求证: .
参考答案与试题解析
1.答案:B
2.答案:D
3.答案:C
4.答案:D
5.答案:B
6.答案:A
7.答案:A
8.答案:B
9.答案:A;60
10.答案:70
11.答案:(2,4)
12.答案:72
13.答案:80
14.答案:60°
15.答案:解:由旋转知:△ADE≌△ABC,
∴∠ACB=∠E,AC=AE,
∴∠E=∠ACE,
又BC∥AE,
∴∠BCE+∠E=180°,
即∠ACB+∠ACE+∠E=180°,
∴∠E=60°,
又AC=AE,
∴△ACE 为等边三角形,
∴∠CAE=60°
又∠BAC=∠DAE
∴∠BAD=∠CAE=60°
又AB=AD
∴△ABD为等边三角形.
16.答案:解:∵Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,
∴BC=
=2 ,
∵∠A=60°,
∴△AA′C是等边三角形,
∴AA′= AB=2,
∴A′C=A′B,
∴∠A′CB=∠A′BC=30°,
∵△A′B′C是△ABC旋转而成,
∴∠A′CB′=90°,BC=B′C,
∴∠B′CB=90°﹣30°=60°,
∴△BCB′是等边三角形,
∴BB′=BC=2
17.答案:证明:连接
四边形 是正方形,
, .
根据旋转得: ,
,
四边形 是正方形
, , 三点共线,
, .
,
在 和 中
, , ,
.
一、单选题
1.如图,在△ABC中,∠BAC=55°,∠C=20°,将△ABC绕点A逆时针旋转α角度(0 α 180°)得到△ADE,若DE AB,则α的值为( )
A.65° B.75° C.85° D.130°
2.如图, 绕点 逆时针旋转90°到 的位置,已知 ,则 的度数为( )
A.55° B.35° C.40° D.45°
3.如图,香港特别行政区区徽中的紫荆花图案,该图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )
A.45° B.60° C.72° D.108°
4.对于平面图形上的任意两点P,Q,如果经过某种变换得到的新图形上的对应点P1,Q1,下列变换中不一定保证PQ=P1Q1的是( )
A.平移 B.旋转 C.翻折 D.位似
5.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
A.70° B.65° C.60° D.55°
6.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.逆时针旋转90° B.顺时针旋转90°
C.逆时针旋转45° D.顺时针旋转45°
7.如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是( )
A.∠AOC B.∠AOD C.∠AOB D.∠BOC
8.如图△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A.2 B. C.3 D.2
二、填空题
9.如图,△ABC≌△ADE,∠C与∠AED都是直角,点E在AB上,∠D=30°,那么△ABC绕着点 逆时针方向旋转 度能与△ADE重合.
10.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.
11.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为 .
12.如图,香港特别行政区区徽由五个相同的花瓣组成,它是以一个花瓣为基本图案通过连续四次旋转所组成,这四次旋转中,旋转角度最小是 °.
13.如图,点D是等腰 的底边AB上的点,若 且 ,将 绕点C逆时针旋转,使它与 重合,则 度
14.如图,△ABD,△AEC 都是等边三角形中,∠BAC=90°,将△ABE 绕点 A 顺时针旋转 可以到△ADC 处.
三、解答题
15.已知:如图,将△ADE绕点A顺时针旋转得到△ABC,点E对应点C恰在D的延长线上,若BC∥AE.求证:△ABD为等边三角形.
16.如图,点A′在Rt△ABC的边AB上,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,A'B'与BC交于点D,连接BB′,求线段BB′的长度.
17.如图,把正方形 绕点 顺时针旋转 到正方形 , 交 于点 ,连接 , .
求证: .
参考答案与试题解析
1.答案:B
2.答案:D
3.答案:C
4.答案:D
5.答案:B
6.答案:A
7.答案:A
8.答案:B
9.答案:A;60
10.答案:70
11.答案:(2,4)
12.答案:72
13.答案:80
14.答案:60°
15.答案:解:由旋转知:△ADE≌△ABC,
∴∠ACB=∠E,AC=AE,
∴∠E=∠ACE,
又BC∥AE,
∴∠BCE+∠E=180°,
即∠ACB+∠ACE+∠E=180°,
∴∠E=60°,
又AC=AE,
∴△ACE 为等边三角形,
∴∠CAE=60°
又∠BAC=∠DAE
∴∠BAD=∠CAE=60°
又AB=AD
∴△ABD为等边三角形.
16.答案:解:∵Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,
∴BC=
=2 ,
∵∠A=60°,
∴△AA′C是等边三角形,
∴AA′= AB=2,
∴A′C=A′B,
∴∠A′CB=∠A′BC=30°,
∵△A′B′C是△ABC旋转而成,
∴∠A′CB′=90°,BC=B′C,
∴∠B′CB=90°﹣30°=60°,
∴△BCB′是等边三角形,
∴BB′=BC=2
17.答案:证明:连接
四边形 是正方形,
, .
根据旋转得: ,
,
四边形 是正方形
, , 三点共线,
, .
,
在 和 中
, , ,
.
