第40讲 与圆有关的计算与证明题 课件(共74张ppt) 2024年中考数学总复习专题突破
文档属性
| 名称 | 第40讲 与圆有关的计算与证明题 课件(共74张ppt) 2024年中考数学总复习专题突破 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 23:23:39 | ||
图片预览









文档简介
复习讲义
第二篇 专题突破
第十部分 解答题重难类型
第40讲 与圆有关的计算与证明题
类型一 圆与全等三角形问题
当关于圆的题目中图形较复杂(如含三角形、四边形等),需要
求线段长度或证明线段、角度相等时,通常会出现全等三角形,因此
可得相等的边、相等的角,为解题提供条件.解题时,要注意切线长定
理的应用.
典题精析
图1
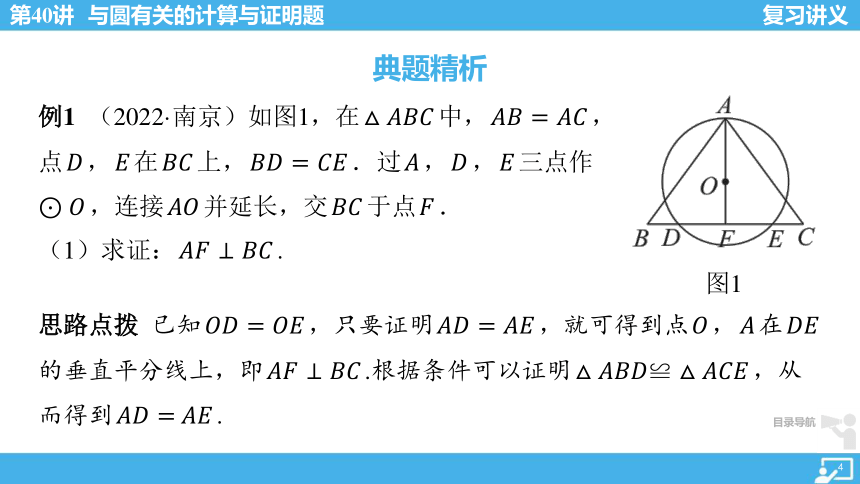
例1 (2022·南京)如图1,在 △???????????? 中, ????????=???????? ,
点 ???? , ???? 在 ???????? 上, ????????=???????? .过 ???? , ???? , ???? 三点作
⊙???? ,连接 ???????? 并延长,交 ???????? 于点 ???? .
?
(1)求证: ????????⊥???????? .
?
思路点拨 已知 ????????=???????? ,只要证明 ????????=???????? ,就可得到点 ???? , ???? 在 ????????
的垂直平分线上,即 ????????⊥???????? .根据条件可以证明 △????????????≌△???????????? ,从
而得到 ????????= ???????? .
?
图128
证明:如图128,连接 ???????? , ???????? , ???????? , ????????.
∵ ????????=???????? , ∴ ∠????=∠???? .
在 △???????????? 和 △???????????? 中, &????????=????????,&∠????=∠????,&??????????=????????,?∴ △????????????≌△????????????SAS.
∴ ????????=???????? .
又 ∵ ????????=???????? , ∴ ???????? 垂直平分 ???????? ,即 ????????⊥???????? .
?
(2)若 ????????=10 , ????????=12 , ????????=2 ,求 ⊙???? 的半径.
?
图1
思路点拨 由(1)知 ????????⊥???????? ,因此可在 Rt△????????????
中利用勾股定理列方程求解.
?
解: ∵ ????????=???????? , ????????⊥???????? , ∴ ????????=????????=12????????=6.
∴ ????????=????????2?????????2=102?62=8.
∵ ????????=2 , ∴ ????????=4 .
设 ????????=????????=???? ,则 ????????=?????????????????=8?????.
∵ ????????2=????????2+????????2 , ∴ ????2=8?????2+42.
∴ ????=5.∴ ⊙???? 的半径为5.
?
针对训练
图2
1.(2022·衡阳)如图2, ???????? 为 ⊙???? 的直径,过圆上一
点 ???? 作 ⊙???? 的切线 ???????? 交 ???????? 的延长线于点 ???? ,过点 ????
作 ????????//???????? 交 ???????? 于点 ???? ,连接 ???????? .
?
(1)直线 ???????? 与 ⊙???? 相切吗?请说明理由.
?
图129
解:直线 ???????? 与 ⊙???? 相切.
理由如下:如图129,连接 ????????.
∵ ???????? 与 ⊙???? 相切于点 ???? , ∴ ∠????????????=90? .
∵ ????????//???????? , ∴ ∠????????????=∠???????????? , ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠???????????? .
又 ∵ ????????=???????? , ????????=???????? , ∴ △????????????≌????????????SAS.
∴ ∠????????????=∠????????????=90? .
∵ ???????? 是 ⊙???? 的半径, ∴ 直线 ???????? 与 ⊙???? 相切.
?
图2
(2)若 ????????=2 , ????????=4 ,求 ???????? 的长.
?
解:设 ⊙???? 的半径为 ???? .
在 Rt△???????????? 中, ????????2+????????2=????????2 , ∴ ????2+42=????+22.
∴ ????=3.
∴ ????????=2????=6.
∴ ????????=????????+????????=2+6=8 .
由(1)得, △????????????≌△???????????? , ∴ ????????=???????? .
在 Rt△???????????? 中, ????????2+????????2=????????2 , ∴ 82+????????2=4+????????2.
∴ 64+????????2=4+????????2.
∴ ????????=6 .
?
图3
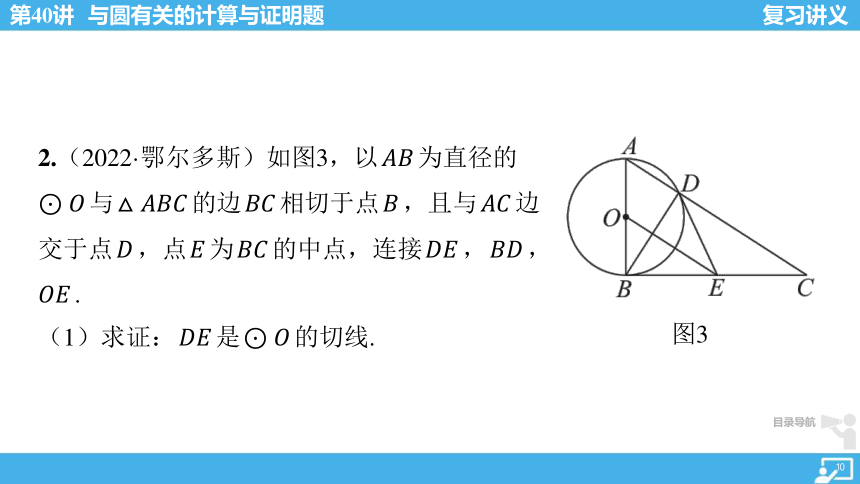
2.(2022·鄂尔多斯)如图3,以 ???????? 为直径的
⊙???? 与 △???????????? 的边 ???????? 相切于点 ???? ,且与 ???????? 边
交于点 ???? ,点 ???? 为 ???????? 的中点,连接 ???????? , ???????? ,
???????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图130
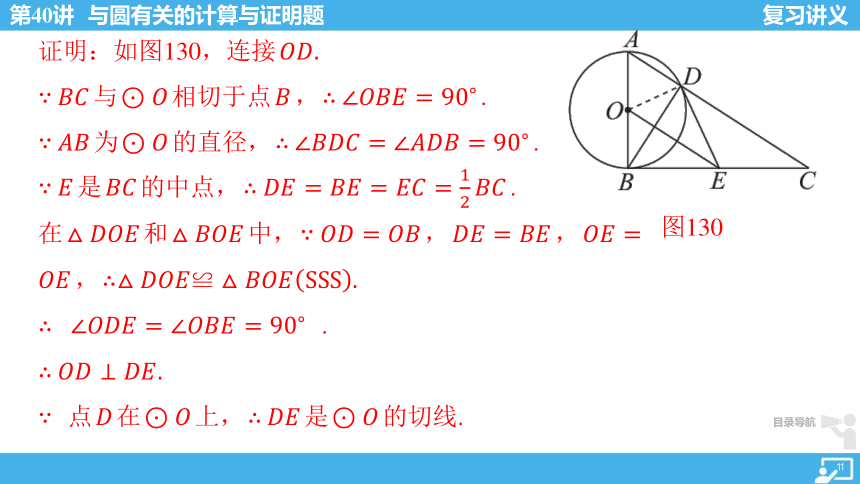
证明:如图130,连接 ????????.
∵ ???????? 与 ⊙???? 相切于点 ???? , ∴ ∠????????????=90? .
∵ ???????? 为 ⊙???? 的直径, ∴ ∠????????????=∠????????????=90? .
∵ ???? 是 ???????? 的中点, ∴ ????????=????????=????????=12???????? .
在 △???????????? 和 △???????????? 中, ∵ ????????=???????? , ????????=???????? , ????????=???????? , ∴ △????????????≌△????????????SSS.
∴ ∠????????????=∠????????????=90? .
∴ ????????⊥????????.
∵ 点 ???? 在 ⊙???? 上, ∴ ???????? 是 ⊙???? 的切线.
?
图3
(2)若 ????????=5 , cos?∠????????????=45 ,求 ???????? 的长.
?
解: ∵ ∠????????????=90? , ∴ ∠????????????+∠????????????=90? .
由(1)知, ????????=2????????=10 , ∠????????????=90? ,
∴ ∠????+∠????????????=90? .
∴ ∠????=∠????????????.
∴ cos??????=cos??∠????????????=45 .
∴ 在 Rt△???????????? 中,????????=????????cos?????=1045=252 .
∵ ????????=???????? , ????????=???????? , ∴ ????????=12????????=254 .
?
类型二 圆与相似三角形问题
由于圆中很容易找到直角或其他相等的角,因此对于圆中判定三
角形相似的问题,通常用证明“两角相等”来解决.利用相似三角形的对
应边成比例和圆的半径相等,可实现线段之间的转化,为解题提供条
件.因此,当题目要求线段的长、线段的比值,或要证明线段间的数量
关系时,通常可以利用圆的性质构造相似三角形解决.
典题精析
图4
例2 (2023·无锡)如图4, ???????? 是 ⊙???? 的直径, ????????
为 ⊙???? 的切线, ???????? 与 ???????? 相交于点 ???? , ????????//???????? ,
交 ???????? 的延长线于点 ???? , ????????=???????? .
?
(1)求 ∠???? 的度数.
?
思路点拨 已知 △???????????? 是等腰三角形,因此求出 ∠???????????? ,就可求出 ∠???? .
已知 ???????? 为 ⊙???? 的切线, ????????//???????? ,则可知 ∠????????????=90? ,因此利用圆
周角定理,可求 ∠???????????? .
?
图131
解:如图131,连接 ????????.
∵ ???????? 为 ⊙???? 的切线, ∴ ∠????????????=90? .
∵ ????????//???????? , ∴ ∠????????????=180??∠????????????=90? .
∴ ∠????????????=12∠????????????=45? .
又 ∵ ????????=???????? , ∴ ∠????=∠????????????=180??45?2=67.5? .
?
图4
(2)若 ?????????????????=8 ,求 ⊙???? 的半径.
?
思路点拨 只要证明 △????????????∽△???????????? ,就可根据对应边成比例和已知等式得出 ????????2 的值.然后在 Rt△???????????? 中利用勾股定理列方程,就可求出 ⊙???? 的半径.
?
图4
解:∵ ????????=???????? , ∠????????????=90? , ∴ ∠????????????=45? .
∵ ∠????????????=45? , ∴ ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? .
∴ ????????2=?????????????????=8 .
又 ∵ ????????>0 , ∴ ????????=22 .
∵ ????????2+????????2=2????????2=????????2=8 , ????????>0 , ∴ ????????=2 ,即 ⊙???? 的半径为2.
?
针对训练
图5
3.如图5, ???????? 是 ⊙???? 的直径,点 ???? 是 ⊙???? 上异于
???? , ???? 的点,连接 ???????? , ???????? ,点 ???? 在 ???????? 的延长线
上,且 ∠????????????=∠???????????? ,点 ???? 在 ???????? 的延长线上,
且 ????????⊥???????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图5
图132
证明:如图132,连接 ????????.
∵ ????????=???????? , ∴ ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ ∠????????????=∠???????????? .
又 ∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? .
∴ ∠????????????+∠????????????=90? .
∴ ∠????????????+∠????????????=90? ,即 ∠????????????=90? .
∴ ????????⊥???????? .
又 ∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
图5
(2)若 ????????????????=23 , ????????=3 ,求 ???????? 的长.
?
解: ∵ ????????????????=23 ,且 ????????=???????? , ∴ 设 ????????=????????=2???? ,则 ????????=3????.
∴ ????????=????????+????????=5????.
∴ ????????????????=35 .
又 ∵ ????????⊥???????? , ????????⊥???????? , ∴ ????????//????????.
∴ △????????????∽△????????????.
∴ ????????????????=????????????????=35 .
又 ∵ ????????=3 , ∴ ????????=95 . ∴ 2????=95 . ∴ ????=910 .
∴ ????????=?????????????????=????=910 ,即 ???????? 的长为 910.
?
图6
4.(2023·营口)如图6,在 △???????????? 中, ????????=???????? ,
以 ???????? 为直径作 ⊙???? 与 ???????? 交于点 ???? ,过点 ???? 作
????????⊥???????? ,交 ???????? 延长线于点 ???? ,垂足为点 ???? .
?
(1)求证: ???????? 为 ⊙???? 的切线.
?
图133
证明:如图133,连接 ???????? , ????????.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? ,即 ????????⊥???????? .
又 ∵ ????????=???????? , ∴ ????????=???????? .
又 ∵ ????????=???????? , ∴ ???????? 是 △???????????? 的中位线.
∴ ????????//????????.∵ ????????⊥???????? , ∴ ????????⊥????????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ????????=3 , cos?????=45 ,求 ???????? 的长.
?
图6
解:在 Rt△???????????? 中, cos?????=????????????????=45 ,可设
????????=4???? ,则 ????????=5???? , ∴ ????????=????????2?????????2=3????.
∵ ????????=???????? , ????????⊥???????? , ∴ ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠????????????=90? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? ,即 33????=3????5???? .
解得 ????=53 .经检验, ????=53 是原方程的解.
∴ ????????=5????=253 .
?
∴ ????????=12????????=256 .
∵ ????????//???????? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? ,即 3256=????????????????+256 .
解得 ????????=757 .
?
图6
类型三 圆与锐角三角函数问题
对于圆与锐角三角函数的压轴题,一般还综合了相似三角形的性
质与判定、勾股定理、圆周角定理、切线的性质与判定等.当求一个角
的三角函数时,需要把这个角转化到直角三角形中求解.注意适当地添
加辅助线是解题的关键.
典题精析
图7
例3 (2023·扬州)如图7,在 △???????????? 中,
∠????????????=90? ,点 ???? 是 ???????? 上一点,且 ∠????????????=12∠???? ,
点 ???? 在 ???????? 上,以点 ???? 为圆心的圆经过 ???? , ???? 两点.
?
(1)试判断直线 ???????? 与 ⊙???? 的位置关系,并说明理由.
?
思路点拨 已知 ???????? 是 ⊙???? 的半径,只要证明 ????????⊥???????? 就可以了.由
∠????????????= 90? ,可知 ∠????+∠????=90? ,因此需要证明 ∠????????????=∠???? .
?
图134
解:直线 ???????? 与 ⊙???? 相切.
理由如下:如图134,连接 ????????.
∵ ∠????????????=12∠???????????? , ∠????????????=12∠???? , ∴ ∠????????????=∠????.
∵ ∠????????????=90? , ∴ ∠????+∠????=90? .
∴ ∠????????????+∠????=90? .
∴ ∠????????????=90? .
∵ ???????? 是 ⊙???? 的半径, ∴ 直线 ???????? 与 ⊙???? 相切.
?
图7
(2)若 sin?????=35 , ⊙???? 的半径为3,求 ???????? 的长.
?
思路点拨 已知 ∠???? 的正弦值,因此分别在 Rt△????????????
和 Rt△???????????? 中,根据锐角三角函数关系列方程求解.
?
解:在 Rt△???????????? 中, sin??????=????????????????=35 , ????????=3 , ∴ ????????=5.
∴ ????????=????????+????????=8 .
在 Rt△???????????? 中, sin??????=????????????????=35 , ∴ 设 ????????=3???? , ????????=5????.
∴ ????????=????????2?????????2=4????=8.
∴ ????=2.
∴ ????????=3????=6 .
?
针对训练
图8
5.(2023·金昌)如图8, △???????????? 内接于 ⊙???? , ???????? 是
⊙???? 的直径, ???? 是 ⊙???? 上的一点, ???????? 平分 ∠???????????? ,
????????⊥???????? ,垂足为点 ???? , ???????? 与 ???????? 相交于点 ???? .
?
图8
(1)求证: ???????? 是 ⊙???? 的切线.
?
证明: ∵ ????????⊥???????? , ∴ ∠????=90? .
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????=∠???????????? .
又 ∠????=∠???? , ∴ ∠????=∠????????????.
∴ ????????//????????.
∴ ∠????????????=180??∠????=90? .
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
图8
(2)当 ⊙???? 的半径为5, sin?????=35 时,求 ???????? 的长.
?
解: ∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? , ????????=2×5=10.
∵ sin??????=????????????????=35 , ∴ ????????=6.
∵ ∠????????????+∠????????????=∠????????????+∠????????????=90? , ∴ ∠????????????=∠????????????=∠????.
∴ sin??∠????????????=sin??????=35 ,即 ????????????????=35 .
解得 ????????=3.6.
∴ ????????=????????2?????????2=4.8 .
?
图9
6.(2023·威海)如图9,在平面直角坐标系中,点 ????
在第一象限内, ⊙???? 与 ???? 轴相切于点 ???? ,与 ???? 轴相交
于点 ????0,8 , ????0,2 .连接 ???????? , ???????? .
?
(1)求点 ???? 的坐标.
?
解: ∵ ????0,8 , ????0,2 , ∴ ????????=6 .
如图135,过点 ???? 作 ????????⊥???????? 于点 ???? , ∴ ????????=????????=3.
∴ ????????=5 .
如图135,连接 ???????? , ????????.
∵ ⊙???? 与 ???? 轴相切于点 ???? , ∴ ????????⊥???? 轴.
∴ ∠????????????=∠????????????=∠????????????=90? .
?
图135
∴ 四边形 ???????????????? 是矩形.
∴ ????????=????????=5.
∴ ????????=????????=5.
∵ ????????=????????2?????????2=4, ∴ 点 ???? 的坐标为 4,5 .
?
图135
(2)求 cos?∠???????????? 的值.
?
图9
图135
解:如图135,连接 ???????? ,并延长交 ⊙???? 于点 ???? ,连接 ???????? ,则 ∠????????????=90? , ????????=2????????=10 , ∴ ????????=????????2?????????2=102?62=8.
∴ cos?∠????????????=cos?∠????????????=????????????????=810=45 .
?
类型四 圆中有关几何图形面积的问题
求圆中几何图形面积的问题,注意运用转化思想.如果所求面积的
图形是规则图形,那么可直接应用相关面积公式计算;如果所求面积
的图形不是规则图形,就要转化为规则图形求解. 在圆中求规则图形的
面积,除了扇形,也会涉及求三角形的面积,有时可以利用圆中的各
种垂直关系直接用面积公式求解,有时可以利用相似三角形的关系求
解.
典题精析
图10
例4 (2023·南通)如图10,等腰三角形 ???????????? 的顶
角 ∠????????????=120? , ⊙???? 与底边 ???????? 相切于点 ???? ,
并与两腰 ???????? , ???????? 分别相交于点 ???? , ???? ,连接
???????? , ???????? .
?
(1)求证:四边形 ???????????????? 是菱形.
?
图10
思路点拨 只要证明 △???????????? 和 △???????????? 都是等边三角形,就可推出四边形 ???????????????? 的四条边相等,从而证得结论.
?
图136
证明:如图136,连接 ????????.
∵ ⊙???? 与底边 ???????? 相切于点 ???? , ∴ ????????⊥????????.
∵ ????????=???????? , ∠????????????=120?, ∴ ∠????????????=∠????????????=12∠????????????=60? .
又 ∵ ????????=???????? , ????????=???????? , ∴ △???????????? 和 △???????????? 都是等边三角形. ∴ ????????=????????=???????? , ????????=????????=????????.
∴ ????????=????????=????????=????????.
∴ 四边形 ???????????????? 是菱形.
?
(2)若 ⊙???? 的半径为2,求图中阴影部分的面积.
?
图10
思路点拨 根据图中阴影部分的面积 = 扇形 ???????????? 的面积-菱形 ???????????????? 的面
积,进行计算即可.
?
图136
解:如图136,连接 ???????? 交 ???????? 于点 ????.
∵ 四边形 ???????????????? 是菱形, ∴ ????????=12????????=1 , ????????=2???????? , ∠????????????=90? .
在 Rt△???????????? 中, ????????=2 , ∴ ????????=????????2?????????2=22?12=3 .
∴ ????????=2????????=23 .
∴ ????阴影=????扇形?????????????????菱形????????????????=120×π×22360?12?????????????????=4π3?12×2×
23?=4π3?23 .
?
针对训练
图11
7.(2022·衢州)如图11, ???? , ???? 是以 ???????? 为直径的
半圆上的两点, ∠????????????=∠???????????? ,连接 ???????? , ???????? .
?
(1)求证: ????????//???????? .
?
证明: ∵ ∠????????????=∠???????????? , ∠????????????=∠???????????? , ∴ ∠????????????=∠????????????.
∴ ????????//???????? .
?
(2)若 ????????=4 , ∠????????????=30? ,求阴影部分的面积.
?
图11
图137
解:如图137,连接 ???????? ,过点 ???? 作 ????????⊥???????? ,垂足为点 ????.
∵ ∠????????????=30? , ∴ ∠????????????=60? .
∴ ∠????????????=180??∠????????????=120? .
∵ ????????=4 , ∴ ????????=????????=2.
∴ ????扇形????????????=120×π×22360=4π3 .
在Rt△???????????? 中, ∵ ????????=??????????sin??60?=2×32=3 , ∴ ????△????????????=12?????????????????=12×2×3=3 .
∴ ????阴影=????扇形?????????????????△????????????=4π3?3 .
?
图12
8.(2023·阜新)如图12, ???????? 是 ⊙???? 的直径, ???? ,
???? 是 ⊙???? 上 ???????? 异侧的两点, ????????⊥???????? ,交 ???????? 的延
长线于点 ???? ,且 ???????? 平分 ∠???????????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图138
证明:如图138,连接 ????????.
∵ ????????⊥???????? , ∴ ∠????=90? .
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠????????????.
∴ ????????//????????.∴ ∠????????????=180??∠????=90? .
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ∠????????????=60? , ????????=4 ,求图中阴影部分的面积.
?
图12
图138
解:如图138,连接 ???????? ,过点 ???? 作 ????????⊥???????? ,垂足
为点 ????.
∵ ∠????????????=60? , ????????=???????? , ∴ △???????????? 是等边三角形.
∴ ????????=????????=????????=12????????=2 , ∠????????????=60? .
在 Rt△???????????? 中, ????????=?????????sin??60?=2×32=3 ,
∴????阴影?=????扇形??????????????????△????????????=60×π×22360?12?????????????????=2π3?12×2×3=2π3?3 .
?
学习至此,请完成备考练习(四十) (第317页)
与圆有关的计算与证明题
类型一 圆与全等三角形问题
图1
1.(2021·百色)如图1, ???????? , ???????? 是 ⊙???? 的切
线,切点分别是 ???? , ???? .过点 ???? 的直线 ????????//???????? ,
交 ⊙???? 于点 ???? , ???? ,交 ???????? 于点 ???? , ???????? 的延长
线交 ???????? 于点 ???? .已知 ????????//???????? .
?
备考练习(四十)
(1)求证: ∠????=45? .
?
图1
图164
证明:如图164,连接 ????????.
∵ ????????//???????? , ????????//???????? , ∴ 四边形 ???????????????? 是平行四边形.
∴ ∠????=∠????.
∵ ???????? 是 ⊙???? 的切线,切点为 ???? , ∴ ????????⊥????????.
∴ ????????⊥???????? .
又 ∵ ????????=???????? , ∴ ∠????=∠????????????=45? .
∴ ∠????=45? .
?
(2)若 ????????=6 ,求 ???????? 的长.
?
图1
图164
解:如图164,连接 ????????.
∵ ???????? , ???????? 是 ⊙???? 的切线,切点分别为 ???? , ???? , ∴ ????????=???????? , ∠????????????=90? .
∵ ???????? 经过圆心 ???? , ∴ ???????? 为 ⊙???? 的直径.
∴ ∠????????????=90? .
∴ ∠????????????=∠????????????.
∴ ∠?????????????∠????????????=∠?????????????∠???????????? ,即∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
?
∴ ∠????????????=∠????????????.
∵ 四边形 ???????????????? 是平行四边形, ∴ ????????=????????.
∴ ????????=????????.
∵ ????????//???????? , ∴ ∠????????????=∠???? .
在 △???????????? 和 △???????????? 中, ∵ ∠????????????=∠???? , ????????=???????? ,∠????????????=∠???????????? , ∴ △????????????≌△????????????ASA.
∴ ????????=????????.
∵ ???????? 是 ⊙???? 的切线, ∴ ????????⊥????????.
∵ ∠????=45? , ????????//???????? , ∴ ∠????????????=∠????=45? .
∴ ????????=????????.
∵ ????????=6 , ∴ ????????=????????=3.
∴ ????????=3.????∴ ????????=3 .
?
图164
图2
2.如图2,四边形 ???????????????? 内接于 ⊙???? , ???????? 是 ⊙???? 的直
径, ???????? 平分 ∠???????????? ,过点 ???? 作 ????????⊥???????? 交 ???????? 的延长
线于点 ???? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图165
证明:如图165,连接 ????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠????????????.
∴ ????????//???????? .
又 ∵ ????????⊥???????? ,即 ????????⊥???????? , ∴ ????????⊥????????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ⊙???? 的半径是5, ????????=8 ,求 ???????? 的长.
?
图2
解:如图165,作 ????????⊥???????? 于点 ????.
∵ ???????? 平分 ∠????????????, ????????⊥???????? , ????????⊥???????? , ∴ ????????=???????? .
在 Rt△???????????? 和 Rt△???????????? 中, &????????=????????,&????????=????????,
∴ Rt△????????????≌Rt△????????????HL.
∴ ????????=????????.
∵ 四边形 ???????????????? 内接于 ⊙????, ∴ ∠????+∠????????????=180? .
又 ∵ ∠????????????+∠????????????=180? , ∴ ∠????=∠???????????? .
?
图165
在 △???????????? 和 △???????????? 中, &∠????????????=∠????????????=90?,&∠????=∠????????????,&??????????=????????,?∴ △????????????≌△????????????AAS.
∴ ????????=????????.
∵ ⊙???? 的半径是5, ∴ ????????=2×5=10 .
设 ????????=????????=???? ,则 ????????=????????+????????=????????+????????=????????+????????+????????=????+8+????=10 .
解得 ????=1.
?
图165
∴ ????????=????????=1.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? .
∴ ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? ,即 ????????1=10???????? .
∴ ????????=10 (负值已舍去).
?
类型二 圆与相似三角形问题
图3
3.(2023·包头)如图3, ???????? 是 ⊙???? 的直径, ???????? 是
弦, ???? 是 ????????? 上一点, ???? 是 ???????? 延长线上一点,连
接 ???????? , ???????? , ???????? .
?
(1)求证: ∠?????????????∠????????????=90? .(请用两种证法解答)
?
图166
证明:(方法一)如图166,连接 ????????.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? .
∵ ∠?????????????∠????????????=∠???????????? , ∠????????????=∠???????????? , ∴ ∠?????????????∠????????????=90? .
(方法二)如图167,连接 ????????.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? . ∵ ∠????????????=∠????????????+∠???????????? ,
∴ ∠?????????????∠????????????=90? .
∵ 四边形 ???????????????? 为⊙???? 的内接四边形,
∴ ∠????????????+∠????????????=180? .
∵ ∠????????????+∠????????????=180? , ∴ ∠????????????=∠????????????.
∴ ∠?????????????∠????????????=90? .
?
(2)若 ∠????????????=∠???????????? , ⊙???? 的半径为3, ????????=4 ,求 ???????? 的长.
?
图3
图167
解:同(1)中方法二知, ∠????????????=∠???????????? ,又∠????????????=∠???????????? , ∴ ∠????????????=∠???????????? ,即 ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ △?????????????△????????????.
∴ ????????????????=???????????????? . ∴ ????????2=?????????????????.
∵ ⊙???? 的半径为3, ∴ ????????=6.
∴ ????????=????????+6 .
又 ∵ ????????=4 , ∴ 42=????????+6????????? .
解得 ????????=2 或 ????????=?8 (舍去) .
∴ ????????=2+6=8 .
?
图4
4.(2023·凉山)如图4, ???????? 是 ⊙???? 的直径,弦????????⊥???????? ,垂足为点 ???? ,点 ???? 是 ???????? 延长线上一点, ????????⊥???????? ,垂足为点 ???? , ∠????????????=∠???????????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图168
证明:如图168,连接 ????????.
∵ ????????⊥???????? , ∴ ∠????????????=90? .
∴ ∠????????????+∠????????????=90? .
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????+∠????????????=90? .
又 ∵ ∠????????????=∠???????????? , ∴ ∠????????????+∠????????????=90? ,即 ∠????????????=90? . ∴ ????????⊥????????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ????????=4 , ????????=2 ,求 ⊙???? 的半径和 ???????? 的长.
?
图4
图168
解:如图168,连接 ????????.
∵ ???????? 是 ⊙???? 的直径,∴ ∠????????????=90? .
∴ ∠????+∠????????????=90? .
又 ∵ ∠????????????+∠????????????=90? , ∴ ∠????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ ∠????=∠???????????? .
又 ∵ ∠????=∠????, ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? .
∵ ???????????=4 , ????????=2 , ∴ 4????????=24 .
?
解得 ????????=8.
∴ ????????=?????????????????=8?2=6.
∴ ⊙???? 的半径为 3.
∴ ????????=????????=3.
∴ ????????=????????+????????=5.
∵ ∠????????????=∠????????????=90? , ∠????=∠???? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? ,即 ????????3=25 .
∴ ????????=65 .
?
图168
类型三 圆与锐角三角函数问题
图5
5.(2023·烟台)如图5,在菱形 ???????????????? 中,对
角线 ???????? , ???????? 相交于点 ???? , ⊙???? 经过 ???? , ???? 两
点,交对角线 ???????? 于点 ???? ,连接 ???????? 交 ???????? 于点
???? ,且 ????????=???????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图169
证明:如图169,连接 ???????? ,则 ????????=???????? , ∴ ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ????????⊥????????.
∴ ∠????????????=90? .
∵ 四边形 ???????????????? 是菱形, ∴ ????????=???????? , ????????⊥???????? ,
∠????????????=∠????????????.
∴ ∠????????????=∠????????????+∠????????????=∠????????????+∠????????????=
180??∠????????????=90? .
∴ ????????⊥???????? .
又 ∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)已知 ⊙???? 的半径与菱形的边长之比为
5:8 ,求 tan?∠???????????? 的值.
?
图5
解: ∵ ????????????????=58 , ????????=2???????? , ∴ ????????2????????=58 .
∴ ????????????????=54 .
设 ????????=4???? ,则 ????????=5???? , ∴ ????????=????????=5????.
∵ ∠????????????=90? , ∴ ????????=????????2?????????2=5????2?4????2=3????.
∴ ????????=?????????????????=5?????3????=2????.
∵ ∠????????????=∠????????????=90? , ∴ ∠????????????=∠????????????=90??∠????????????.
∴ tan?∠????????????=tan?∠????????????=????????????????=4????2????=2 .
?
图6
6.(2023·宁夏)如图6,已知 ???????? 是 ⊙???? 的直径,直
线 ???????? 是 ⊙???? 的切线,切点为 ???? , ????????⊥???????? ,垂足
为点 ???? ,连接 ???????? .
?
(1)求证: ???????? 平分 ∠???????????? .
?
图170
证明:如图170,连接 ???????? .
∵ 直线 ???????? 是 ⊙???? 的切线,切点为 ???? , ∴ ????????⊥???????? .
又 ∵ ????????⊥???????? ,垂足为点 ???? , ∴ ????????//????????.
∴ ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠????????????.
∴ ???????? 平分 ∠???????????? .
?
(2)若 ????????=5 , tan?∠????????????=34 ,求 ⊙???? 的半径.
?
图6
解:如图170,连接 ????????.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? .
又 ∵ ????????⊥???????? ,由(1)得 ∠????????????=∠???????????? , ∴ ∠????????????=
∠???????????? .
在 Rt△???????????? 中, tan?∠????????????=tan?∠????????????=34 , ∴ ????????????????=
5????????=34 .
∴ ????????=203 .
在 Rt△???????????? 中, ????????=????????2+????????2=253 , ∴ ⊙???? 的半径为 256 .
?
图170
类型四 圆中有关几何图形面积的问题
图7
7.(2023·十堰)如图7,在 Rt△???????????? 中,
∠????=90? , ????????=???????? ,点 ???? 在 ???????? 上,以点 ???? 为
圆心, ???????? 长为半径的半圆分别交 ???????? , ???????? , ????????
于点 ???? , ???? , ???? ,且点 ???? 是 ????????? 的中点.
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图7
图171
证明:如图171,连接 ???????? , ????????.
∵ ∠????=90? , ????????=???????? , ∴ ∠????????????=∠????=45? .
∵ ????????=????????, ∴ ∠????????????=∠????????????=45? .
∴ ∠????????????=90? .
∵ 点 ???? 是 ????????? 的中点, ∴ ∠????????????=∠????????????=12∠????????????=45? .
∴ ∠????????????=180??∠?????????????∠????=90? .
∴ ????????⊥????????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
图7
(2)若 ????????=2 ,求图中阴影部分的面积(结
果保留 π ).
?
解: ∵ ????????⊥???????? , ∠????=45? , ∴ △???????????? 是等
腰直角三角形.
设 ????????=????????=???? ,则 ????????=2???? , ∴ ????????=????+2????.
∵ ????????=2???????? , ∴ ????+2????=22+????.
解得 ????=2.
∴ ????阴影=????△?????????????????扇形????????????=12×2×2?45×π×22360=2?π2 .
?
图8
8.(2023·齐齐哈尔)如图8,在 Rt△???????????? 中,
∠????=90? , ???????? 平分 ∠???????????? 交 ???????? 于点 ???? ,点 ???? 是
斜边 ???????? 上一点,以 ???????? 为直径的 ⊙???? 经过点 ???? ,交
???????? 于点 ???? ,连接 ???????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图8
图172
证明:如图172,连接 ????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠????????????.∴ ????????//????????.
∴ ∠????????????=∠????=90? .
∴ ????????⊥???????? 于点 ????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ????????=5 , tan?∠????????????=3 ,求图中阴影部分的面积(结果保留 π ).
?
图8
图172
解:如图172,连接 ???????? , ????????.
∵ ∠????=90? , tan?∠????????????=3 , ∴ ∠????????????=60? .
∴ ∠????????????=90??∠????????????=30? .
又 ∵ ????????=5 , ∴ ????????=2????????=10.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90?.
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????=30?.
?
在 Rt△???????????? 中, ????????=10 ,cos?∠????????????=????????????????=32 , ∴ ????????=2033 .
∴ ????????=12????????=1033 .
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=2∠????????????=60?.
又 ∵ ????????=???????? , ∴ △???????????? 是等边三角形.
∴ ∠????????????=60? .
∵ ????????//???????? , ∴ ????△????????????=????△????????????.
∴ ????阴影=????扇形????????????=60×π×10332360=50π9 .
?
图172
第二篇 专题突破
第十部分 解答题重难类型
第40讲 与圆有关的计算与证明题
类型一 圆与全等三角形问题
当关于圆的题目中图形较复杂(如含三角形、四边形等),需要
求线段长度或证明线段、角度相等时,通常会出现全等三角形,因此
可得相等的边、相等的角,为解题提供条件.解题时,要注意切线长定
理的应用.
典题精析
图1
例1 (2022·南京)如图1,在 △???????????? 中, ????????=???????? ,
点 ???? , ???? 在 ???????? 上, ????????=???????? .过 ???? , ???? , ???? 三点作
⊙???? ,连接 ???????? 并延长,交 ???????? 于点 ???? .
?
(1)求证: ????????⊥???????? .
?
思路点拨 已知 ????????=???????? ,只要证明 ????????=???????? ,就可得到点 ???? , ???? 在 ????????
的垂直平分线上,即 ????????⊥???????? .根据条件可以证明 △????????????≌△???????????? ,从
而得到 ????????= ???????? .
?
图128
证明:如图128,连接 ???????? , ???????? , ???????? , ????????.
∵ ????????=???????? , ∴ ∠????=∠???? .
在 △???????????? 和 △???????????? 中, &????????=????????,&∠????=∠????,&??????????=????????,?∴ △????????????≌△????????????SAS.
∴ ????????=???????? .
又 ∵ ????????=???????? , ∴ ???????? 垂直平分 ???????? ,即 ????????⊥???????? .
?
(2)若 ????????=10 , ????????=12 , ????????=2 ,求 ⊙???? 的半径.
?
图1
思路点拨 由(1)知 ????????⊥???????? ,因此可在 Rt△????????????
中利用勾股定理列方程求解.
?
解: ∵ ????????=???????? , ????????⊥???????? , ∴ ????????=????????=12????????=6.
∴ ????????=????????2?????????2=102?62=8.
∵ ????????=2 , ∴ ????????=4 .
设 ????????=????????=???? ,则 ????????=?????????????????=8?????.
∵ ????????2=????????2+????????2 , ∴ ????2=8?????2+42.
∴ ????=5.∴ ⊙???? 的半径为5.
?
针对训练
图2
1.(2022·衡阳)如图2, ???????? 为 ⊙???? 的直径,过圆上一
点 ???? 作 ⊙???? 的切线 ???????? 交 ???????? 的延长线于点 ???? ,过点 ????
作 ????????//???????? 交 ???????? 于点 ???? ,连接 ???????? .
?
(1)直线 ???????? 与 ⊙???? 相切吗?请说明理由.
?
图129
解:直线 ???????? 与 ⊙???? 相切.
理由如下:如图129,连接 ????????.
∵ ???????? 与 ⊙???? 相切于点 ???? , ∴ ∠????????????=90? .
∵ ????????//???????? , ∴ ∠????????????=∠???????????? , ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠???????????? .
又 ∵ ????????=???????? , ????????=???????? , ∴ △????????????≌????????????SAS.
∴ ∠????????????=∠????????????=90? .
∵ ???????? 是 ⊙???? 的半径, ∴ 直线 ???????? 与 ⊙???? 相切.
?
图2
(2)若 ????????=2 , ????????=4 ,求 ???????? 的长.
?
解:设 ⊙???? 的半径为 ???? .
在 Rt△???????????? 中, ????????2+????????2=????????2 , ∴ ????2+42=????+22.
∴ ????=3.
∴ ????????=2????=6.
∴ ????????=????????+????????=2+6=8 .
由(1)得, △????????????≌△???????????? , ∴ ????????=???????? .
在 Rt△???????????? 中, ????????2+????????2=????????2 , ∴ 82+????????2=4+????????2.
∴ 64+????????2=4+????????2.
∴ ????????=6 .
?
图3
2.(2022·鄂尔多斯)如图3,以 ???????? 为直径的
⊙???? 与 △???????????? 的边 ???????? 相切于点 ???? ,且与 ???????? 边
交于点 ???? ,点 ???? 为 ???????? 的中点,连接 ???????? , ???????? ,
???????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图130
证明:如图130,连接 ????????.
∵ ???????? 与 ⊙???? 相切于点 ???? , ∴ ∠????????????=90? .
∵ ???????? 为 ⊙???? 的直径, ∴ ∠????????????=∠????????????=90? .
∵ ???? 是 ???????? 的中点, ∴ ????????=????????=????????=12???????? .
在 △???????????? 和 △???????????? 中, ∵ ????????=???????? , ????????=???????? , ????????=???????? , ∴ △????????????≌△????????????SSS.
∴ ∠????????????=∠????????????=90? .
∴ ????????⊥????????.
∵ 点 ???? 在 ⊙???? 上, ∴ ???????? 是 ⊙???? 的切线.
?
图3
(2)若 ????????=5 , cos?∠????????????=45 ,求 ???????? 的长.
?
解: ∵ ∠????????????=90? , ∴ ∠????????????+∠????????????=90? .
由(1)知, ????????=2????????=10 , ∠????????????=90? ,
∴ ∠????+∠????????????=90? .
∴ ∠????=∠????????????.
∴ cos??????=cos??∠????????????=45 .
∴ 在 Rt△???????????? 中,????????=????????cos?????=1045=252 .
∵ ????????=???????? , ????????=???????? , ∴ ????????=12????????=254 .
?
类型二 圆与相似三角形问题
由于圆中很容易找到直角或其他相等的角,因此对于圆中判定三
角形相似的问题,通常用证明“两角相等”来解决.利用相似三角形的对
应边成比例和圆的半径相等,可实现线段之间的转化,为解题提供条
件.因此,当题目要求线段的长、线段的比值,或要证明线段间的数量
关系时,通常可以利用圆的性质构造相似三角形解决.
典题精析
图4
例2 (2023·无锡)如图4, ???????? 是 ⊙???? 的直径, ????????
为 ⊙???? 的切线, ???????? 与 ???????? 相交于点 ???? , ????????//???????? ,
交 ???????? 的延长线于点 ???? , ????????=???????? .
?
(1)求 ∠???? 的度数.
?
思路点拨 已知 △???????????? 是等腰三角形,因此求出 ∠???????????? ,就可求出 ∠???? .
已知 ???????? 为 ⊙???? 的切线, ????????//???????? ,则可知 ∠????????????=90? ,因此利用圆
周角定理,可求 ∠???????????? .
?
图131
解:如图131,连接 ????????.
∵ ???????? 为 ⊙???? 的切线, ∴ ∠????????????=90? .
∵ ????????//???????? , ∴ ∠????????????=180??∠????????????=90? .
∴ ∠????????????=12∠????????????=45? .
又 ∵ ????????=???????? , ∴ ∠????=∠????????????=180??45?2=67.5? .
?
图4
(2)若 ?????????????????=8 ,求 ⊙???? 的半径.
?
思路点拨 只要证明 △????????????∽△???????????? ,就可根据对应边成比例和已知等式得出 ????????2 的值.然后在 Rt△???????????? 中利用勾股定理列方程,就可求出 ⊙???? 的半径.
?
图4
解:∵ ????????=???????? , ∠????????????=90? , ∴ ∠????????????=45? .
∵ ∠????????????=45? , ∴ ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? .
∴ ????????2=?????????????????=8 .
又 ∵ ????????>0 , ∴ ????????=22 .
∵ ????????2+????????2=2????????2=????????2=8 , ????????>0 , ∴ ????????=2 ,即 ⊙???? 的半径为2.
?
针对训练
图5
3.如图5, ???????? 是 ⊙???? 的直径,点 ???? 是 ⊙???? 上异于
???? , ???? 的点,连接 ???????? , ???????? ,点 ???? 在 ???????? 的延长线
上,且 ∠????????????=∠???????????? ,点 ???? 在 ???????? 的延长线上,
且 ????????⊥???????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图5
图132
证明:如图132,连接 ????????.
∵ ????????=???????? , ∴ ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ ∠????????????=∠???????????? .
又 ∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? .
∴ ∠????????????+∠????????????=90? .
∴ ∠????????????+∠????????????=90? ,即 ∠????????????=90? .
∴ ????????⊥???????? .
又 ∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
图5
(2)若 ????????????????=23 , ????????=3 ,求 ???????? 的长.
?
解: ∵ ????????????????=23 ,且 ????????=???????? , ∴ 设 ????????=????????=2???? ,则 ????????=3????.
∴ ????????=????????+????????=5????.
∴ ????????????????=35 .
又 ∵ ????????⊥???????? , ????????⊥???????? , ∴ ????????//????????.
∴ △????????????∽△????????????.
∴ ????????????????=????????????????=35 .
又 ∵ ????????=3 , ∴ ????????=95 . ∴ 2????=95 . ∴ ????=910 .
∴ ????????=?????????????????=????=910 ,即 ???????? 的长为 910.
?
图6
4.(2023·营口)如图6,在 △???????????? 中, ????????=???????? ,
以 ???????? 为直径作 ⊙???? 与 ???????? 交于点 ???? ,过点 ???? 作
????????⊥???????? ,交 ???????? 延长线于点 ???? ,垂足为点 ???? .
?
(1)求证: ???????? 为 ⊙???? 的切线.
?
图133
证明:如图133,连接 ???????? , ????????.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? ,即 ????????⊥???????? .
又 ∵ ????????=???????? , ∴ ????????=???????? .
又 ∵ ????????=???????? , ∴ ???????? 是 △???????????? 的中位线.
∴ ????????//????????.∵ ????????⊥???????? , ∴ ????????⊥????????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ????????=3 , cos?????=45 ,求 ???????? 的长.
?
图6
解:在 Rt△???????????? 中, cos?????=????????????????=45 ,可设
????????=4???? ,则 ????????=5???? , ∴ ????????=????????2?????????2=3????.
∵ ????????=???????? , ????????⊥???????? , ∴ ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠????????????=90? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? ,即 33????=3????5???? .
解得 ????=53 .经检验, ????=53 是原方程的解.
∴ ????????=5????=253 .
?
∴ ????????=12????????=256 .
∵ ????????//???????? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? ,即 3256=????????????????+256 .
解得 ????????=757 .
?
图6
类型三 圆与锐角三角函数问题
对于圆与锐角三角函数的压轴题,一般还综合了相似三角形的性
质与判定、勾股定理、圆周角定理、切线的性质与判定等.当求一个角
的三角函数时,需要把这个角转化到直角三角形中求解.注意适当地添
加辅助线是解题的关键.
典题精析
图7
例3 (2023·扬州)如图7,在 △???????????? 中,
∠????????????=90? ,点 ???? 是 ???????? 上一点,且 ∠????????????=12∠???? ,
点 ???? 在 ???????? 上,以点 ???? 为圆心的圆经过 ???? , ???? 两点.
?
(1)试判断直线 ???????? 与 ⊙???? 的位置关系,并说明理由.
?
思路点拨 已知 ???????? 是 ⊙???? 的半径,只要证明 ????????⊥???????? 就可以了.由
∠????????????= 90? ,可知 ∠????+∠????=90? ,因此需要证明 ∠????????????=∠???? .
?
图134
解:直线 ???????? 与 ⊙???? 相切.
理由如下:如图134,连接 ????????.
∵ ∠????????????=12∠???????????? , ∠????????????=12∠???? , ∴ ∠????????????=∠????.
∵ ∠????????????=90? , ∴ ∠????+∠????=90? .
∴ ∠????????????+∠????=90? .
∴ ∠????????????=90? .
∵ ???????? 是 ⊙???? 的半径, ∴ 直线 ???????? 与 ⊙???? 相切.
?
图7
(2)若 sin?????=35 , ⊙???? 的半径为3,求 ???????? 的长.
?
思路点拨 已知 ∠???? 的正弦值,因此分别在 Rt△????????????
和 Rt△???????????? 中,根据锐角三角函数关系列方程求解.
?
解:在 Rt△???????????? 中, sin??????=????????????????=35 , ????????=3 , ∴ ????????=5.
∴ ????????=????????+????????=8 .
在 Rt△???????????? 中, sin??????=????????????????=35 , ∴ 设 ????????=3???? , ????????=5????.
∴ ????????=????????2?????????2=4????=8.
∴ ????=2.
∴ ????????=3????=6 .
?
针对训练
图8
5.(2023·金昌)如图8, △???????????? 内接于 ⊙???? , ???????? 是
⊙???? 的直径, ???? 是 ⊙???? 上的一点, ???????? 平分 ∠???????????? ,
????????⊥???????? ,垂足为点 ???? , ???????? 与 ???????? 相交于点 ???? .
?
图8
(1)求证: ???????? 是 ⊙???? 的切线.
?
证明: ∵ ????????⊥???????? , ∴ ∠????=90? .
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????=∠???????????? .
又 ∠????=∠???? , ∴ ∠????=∠????????????.
∴ ????????//????????.
∴ ∠????????????=180??∠????=90? .
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
图8
(2)当 ⊙???? 的半径为5, sin?????=35 时,求 ???????? 的长.
?
解: ∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? , ????????=2×5=10.
∵ sin??????=????????????????=35 , ∴ ????????=6.
∵ ∠????????????+∠????????????=∠????????????+∠????????????=90? , ∴ ∠????????????=∠????????????=∠????.
∴ sin??∠????????????=sin??????=35 ,即 ????????????????=35 .
解得 ????????=3.6.
∴ ????????=????????2?????????2=4.8 .
?
图9
6.(2023·威海)如图9,在平面直角坐标系中,点 ????
在第一象限内, ⊙???? 与 ???? 轴相切于点 ???? ,与 ???? 轴相交
于点 ????0,8 , ????0,2 .连接 ???????? , ???????? .
?
(1)求点 ???? 的坐标.
?
解: ∵ ????0,8 , ????0,2 , ∴ ????????=6 .
如图135,过点 ???? 作 ????????⊥???????? 于点 ???? , ∴ ????????=????????=3.
∴ ????????=5 .
如图135,连接 ???????? , ????????.
∵ ⊙???? 与 ???? 轴相切于点 ???? , ∴ ????????⊥???? 轴.
∴ ∠????????????=∠????????????=∠????????????=90? .
?
图135
∴ 四边形 ???????????????? 是矩形.
∴ ????????=????????=5.
∴ ????????=????????=5.
∵ ????????=????????2?????????2=4, ∴ 点 ???? 的坐标为 4,5 .
?
图135
(2)求 cos?∠???????????? 的值.
?
图9
图135
解:如图135,连接 ???????? ,并延长交 ⊙???? 于点 ???? ,连接 ???????? ,则 ∠????????????=90? , ????????=2????????=10 , ∴ ????????=????????2?????????2=102?62=8.
∴ cos?∠????????????=cos?∠????????????=????????????????=810=45 .
?
类型四 圆中有关几何图形面积的问题
求圆中几何图形面积的问题,注意运用转化思想.如果所求面积的
图形是规则图形,那么可直接应用相关面积公式计算;如果所求面积
的图形不是规则图形,就要转化为规则图形求解. 在圆中求规则图形的
面积,除了扇形,也会涉及求三角形的面积,有时可以利用圆中的各
种垂直关系直接用面积公式求解,有时可以利用相似三角形的关系求
解.
典题精析
图10
例4 (2023·南通)如图10,等腰三角形 ???????????? 的顶
角 ∠????????????=120? , ⊙???? 与底边 ???????? 相切于点 ???? ,
并与两腰 ???????? , ???????? 分别相交于点 ???? , ???? ,连接
???????? , ???????? .
?
(1)求证:四边形 ???????????????? 是菱形.
?
图10
思路点拨 只要证明 △???????????? 和 △???????????? 都是等边三角形,就可推出四边形 ???????????????? 的四条边相等,从而证得结论.
?
图136
证明:如图136,连接 ????????.
∵ ⊙???? 与底边 ???????? 相切于点 ???? , ∴ ????????⊥????????.
∵ ????????=???????? , ∠????????????=120?, ∴ ∠????????????=∠????????????=12∠????????????=60? .
又 ∵ ????????=???????? , ????????=???????? , ∴ △???????????? 和 △???????????? 都是等边三角形. ∴ ????????=????????=???????? , ????????=????????=????????.
∴ ????????=????????=????????=????????.
∴ 四边形 ???????????????? 是菱形.
?
(2)若 ⊙???? 的半径为2,求图中阴影部分的面积.
?
图10
思路点拨 根据图中阴影部分的面积 = 扇形 ???????????? 的面积-菱形 ???????????????? 的面
积,进行计算即可.
?
图136
解:如图136,连接 ???????? 交 ???????? 于点 ????.
∵ 四边形 ???????????????? 是菱形, ∴ ????????=12????????=1 , ????????=2???????? , ∠????????????=90? .
在 Rt△???????????? 中, ????????=2 , ∴ ????????=????????2?????????2=22?12=3 .
∴ ????????=2????????=23 .
∴ ????阴影=????扇形?????????????????菱形????????????????=120×π×22360?12?????????????????=4π3?12×2×
23?=4π3?23 .
?
针对训练
图11
7.(2022·衢州)如图11, ???? , ???? 是以 ???????? 为直径的
半圆上的两点, ∠????????????=∠???????????? ,连接 ???????? , ???????? .
?
(1)求证: ????????//???????? .
?
证明: ∵ ∠????????????=∠???????????? , ∠????????????=∠???????????? , ∴ ∠????????????=∠????????????.
∴ ????????//???????? .
?
(2)若 ????????=4 , ∠????????????=30? ,求阴影部分的面积.
?
图11
图137
解:如图137,连接 ???????? ,过点 ???? 作 ????????⊥???????? ,垂足为点 ????.
∵ ∠????????????=30? , ∴ ∠????????????=60? .
∴ ∠????????????=180??∠????????????=120? .
∵ ????????=4 , ∴ ????????=????????=2.
∴ ????扇形????????????=120×π×22360=4π3 .
在Rt△???????????? 中, ∵ ????????=??????????sin??60?=2×32=3 , ∴ ????△????????????=12?????????????????=12×2×3=3 .
∴ ????阴影=????扇形?????????????????△????????????=4π3?3 .
?
图12
8.(2023·阜新)如图12, ???????? 是 ⊙???? 的直径, ???? ,
???? 是 ⊙???? 上 ???????? 异侧的两点, ????????⊥???????? ,交 ???????? 的延
长线于点 ???? ,且 ???????? 平分 ∠???????????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图138
证明:如图138,连接 ????????.
∵ ????????⊥???????? , ∴ ∠????=90? .
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠????????????.
∴ ????????//????????.∴ ∠????????????=180??∠????=90? .
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ∠????????????=60? , ????????=4 ,求图中阴影部分的面积.
?
图12
图138
解:如图138,连接 ???????? ,过点 ???? 作 ????????⊥???????? ,垂足
为点 ????.
∵ ∠????????????=60? , ????????=???????? , ∴ △???????????? 是等边三角形.
∴ ????????=????????=????????=12????????=2 , ∠????????????=60? .
在 Rt△???????????? 中, ????????=?????????sin??60?=2×32=3 ,
∴????阴影?=????扇形??????????????????△????????????=60×π×22360?12?????????????????=2π3?12×2×3=2π3?3 .
?
学习至此,请完成备考练习(四十) (第317页)
与圆有关的计算与证明题
类型一 圆与全等三角形问题
图1
1.(2021·百色)如图1, ???????? , ???????? 是 ⊙???? 的切
线,切点分别是 ???? , ???? .过点 ???? 的直线 ????????//???????? ,
交 ⊙???? 于点 ???? , ???? ,交 ???????? 于点 ???? , ???????? 的延长
线交 ???????? 于点 ???? .已知 ????????//???????? .
?
备考练习(四十)
(1)求证: ∠????=45? .
?
图1
图164
证明:如图164,连接 ????????.
∵ ????????//???????? , ????????//???????? , ∴ 四边形 ???????????????? 是平行四边形.
∴ ∠????=∠????.
∵ ???????? 是 ⊙???? 的切线,切点为 ???? , ∴ ????????⊥????????.
∴ ????????⊥???????? .
又 ∵ ????????=???????? , ∴ ∠????=∠????????????=45? .
∴ ∠????=45? .
?
(2)若 ????????=6 ,求 ???????? 的长.
?
图1
图164
解:如图164,连接 ????????.
∵ ???????? , ???????? 是 ⊙???? 的切线,切点分别为 ???? , ???? , ∴ ????????=???????? , ∠????????????=90? .
∵ ???????? 经过圆心 ???? , ∴ ???????? 为 ⊙???? 的直径.
∴ ∠????????????=90? .
∴ ∠????????????=∠????????????.
∴ ∠?????????????∠????????????=∠?????????????∠???????????? ,即∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
?
∴ ∠????????????=∠????????????.
∵ 四边形 ???????????????? 是平行四边形, ∴ ????????=????????.
∴ ????????=????????.
∵ ????????//???????? , ∴ ∠????????????=∠???? .
在 △???????????? 和 △???????????? 中, ∵ ∠????????????=∠???? , ????????=???????? ,∠????????????=∠???????????? , ∴ △????????????≌△????????????ASA.
∴ ????????=????????.
∵ ???????? 是 ⊙???? 的切线, ∴ ????????⊥????????.
∵ ∠????=45? , ????????//???????? , ∴ ∠????????????=∠????=45? .
∴ ????????=????????.
∵ ????????=6 , ∴ ????????=????????=3.
∴ ????????=3.????∴ ????????=3 .
?
图164
图2
2.如图2,四边形 ???????????????? 内接于 ⊙???? , ???????? 是 ⊙???? 的直
径, ???????? 平分 ∠???????????? ,过点 ???? 作 ????????⊥???????? 交 ???????? 的延长
线于点 ???? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图165
证明:如图165,连接 ????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠????????????.
∴ ????????//???????? .
又 ∵ ????????⊥???????? ,即 ????????⊥???????? , ∴ ????????⊥????????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ⊙???? 的半径是5, ????????=8 ,求 ???????? 的长.
?
图2
解:如图165,作 ????????⊥???????? 于点 ????.
∵ ???????? 平分 ∠????????????, ????????⊥???????? , ????????⊥???????? , ∴ ????????=???????? .
在 Rt△???????????? 和 Rt△???????????? 中, &????????=????????,&????????=????????,
∴ Rt△????????????≌Rt△????????????HL.
∴ ????????=????????.
∵ 四边形 ???????????????? 内接于 ⊙????, ∴ ∠????+∠????????????=180? .
又 ∵ ∠????????????+∠????????????=180? , ∴ ∠????=∠???????????? .
?
图165
在 △???????????? 和 △???????????? 中, &∠????????????=∠????????????=90?,&∠????=∠????????????,&??????????=????????,?∴ △????????????≌△????????????AAS.
∴ ????????=????????.
∵ ⊙???? 的半径是5, ∴ ????????=2×5=10 .
设 ????????=????????=???? ,则 ????????=????????+????????=????????+????????=????????+????????+????????=????+8+????=10 .
解得 ????=1.
?
图165
∴ ????????=????????=1.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? .
∴ ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? ,即 ????????1=10???????? .
∴ ????????=10 (负值已舍去).
?
类型二 圆与相似三角形问题
图3
3.(2023·包头)如图3, ???????? 是 ⊙???? 的直径, ???????? 是
弦, ???? 是 ????????? 上一点, ???? 是 ???????? 延长线上一点,连
接 ???????? , ???????? , ???????? .
?
(1)求证: ∠?????????????∠????????????=90? .(请用两种证法解答)
?
图166
证明:(方法一)如图166,连接 ????????.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? .
∵ ∠?????????????∠????????????=∠???????????? , ∠????????????=∠???????????? , ∴ ∠?????????????∠????????????=90? .
(方法二)如图167,连接 ????????.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? . ∵ ∠????????????=∠????????????+∠???????????? ,
∴ ∠?????????????∠????????????=90? .
∵ 四边形 ???????????????? 为⊙???? 的内接四边形,
∴ ∠????????????+∠????????????=180? .
∵ ∠????????????+∠????????????=180? , ∴ ∠????????????=∠????????????.
∴ ∠?????????????∠????????????=90? .
?
(2)若 ∠????????????=∠???????????? , ⊙???? 的半径为3, ????????=4 ,求 ???????? 的长.
?
图3
图167
解:同(1)中方法二知, ∠????????????=∠???????????? ,又∠????????????=∠???????????? , ∴ ∠????????????=∠???????????? ,即 ∠????????????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ △?????????????△????????????.
∴ ????????????????=???????????????? . ∴ ????????2=?????????????????.
∵ ⊙???? 的半径为3, ∴ ????????=6.
∴ ????????=????????+6 .
又 ∵ ????????=4 , ∴ 42=????????+6????????? .
解得 ????????=2 或 ????????=?8 (舍去) .
∴ ????????=2+6=8 .
?
图4
4.(2023·凉山)如图4, ???????? 是 ⊙???? 的直径,弦????????⊥???????? ,垂足为点 ???? ,点 ???? 是 ???????? 延长线上一点, ????????⊥???????? ,垂足为点 ???? , ∠????????????=∠???????????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图168
证明:如图168,连接 ????????.
∵ ????????⊥???????? , ∴ ∠????????????=90? .
∴ ∠????????????+∠????????????=90? .
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????+∠????????????=90? .
又 ∵ ∠????????????=∠???????????? , ∴ ∠????????????+∠????????????=90? ,即 ∠????????????=90? . ∴ ????????⊥????????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ????????=4 , ????????=2 ,求 ⊙???? 的半径和 ???????? 的长.
?
图4
图168
解:如图168,连接 ????????.
∵ ???????? 是 ⊙???? 的直径,∴ ∠????????????=90? .
∴ ∠????+∠????????????=90? .
又 ∵ ∠????????????+∠????????????=90? , ∴ ∠????=∠???????????? .
又 ∵ ∠????????????=∠???????????? , ∴ ∠????=∠???????????? .
又 ∵ ∠????=∠????, ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? .
∵ ???????????=4 , ????????=2 , ∴ 4????????=24 .
?
解得 ????????=8.
∴ ????????=?????????????????=8?2=6.
∴ ⊙???? 的半径为 3.
∴ ????????=????????=3.
∴ ????????=????????+????????=5.
∵ ∠????????????=∠????????????=90? , ∠????=∠???? , ∴ △????????????∽△????????????.
∴ ????????????????=???????????????? ,即 ????????3=25 .
∴ ????????=65 .
?
图168
类型三 圆与锐角三角函数问题
图5
5.(2023·烟台)如图5,在菱形 ???????????????? 中,对
角线 ???????? , ???????? 相交于点 ???? , ⊙???? 经过 ???? , ???? 两
点,交对角线 ???????? 于点 ???? ,连接 ???????? 交 ???????? 于点
???? ,且 ????????=???????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图169
证明:如图169,连接 ???????? ,则 ????????=???????? , ∴ ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ????????⊥????????.
∴ ∠????????????=90? .
∵ 四边形 ???????????????? 是菱形, ∴ ????????=???????? , ????????⊥???????? ,
∠????????????=∠????????????.
∴ ∠????????????=∠????????????+∠????????????=∠????????????+∠????????????=
180??∠????????????=90? .
∴ ????????⊥???????? .
又 ∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)已知 ⊙???? 的半径与菱形的边长之比为
5:8 ,求 tan?∠???????????? 的值.
?
图5
解: ∵ ????????????????=58 , ????????=2???????? , ∴ ????????2????????=58 .
∴ ????????????????=54 .
设 ????????=4???? ,则 ????????=5???? , ∴ ????????=????????=5????.
∵ ∠????????????=90? , ∴ ????????=????????2?????????2=5????2?4????2=3????.
∴ ????????=?????????????????=5?????3????=2????.
∵ ∠????????????=∠????????????=90? , ∴ ∠????????????=∠????????????=90??∠????????????.
∴ tan?∠????????????=tan?∠????????????=????????????????=4????2????=2 .
?
图6
6.(2023·宁夏)如图6,已知 ???????? 是 ⊙???? 的直径,直
线 ???????? 是 ⊙???? 的切线,切点为 ???? , ????????⊥???????? ,垂足
为点 ???? ,连接 ???????? .
?
(1)求证: ???????? 平分 ∠???????????? .
?
图170
证明:如图170,连接 ???????? .
∵ 直线 ???????? 是 ⊙???? 的切线,切点为 ???? , ∴ ????????⊥???????? .
又 ∵ ????????⊥???????? ,垂足为点 ???? , ∴ ????????//????????.
∴ ∠????????????=∠????????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠????????????.
∴ ???????? 平分 ∠???????????? .
?
(2)若 ????????=5 , tan?∠????????????=34 ,求 ⊙???? 的半径.
?
图6
解:如图170,连接 ????????.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90? .
又 ∵ ????????⊥???????? ,由(1)得 ∠????????????=∠???????????? , ∴ ∠????????????=
∠???????????? .
在 Rt△???????????? 中, tan?∠????????????=tan?∠????????????=34 , ∴ ????????????????=
5????????=34 .
∴ ????????=203 .
在 Rt△???????????? 中, ????????=????????2+????????2=253 , ∴ ⊙???? 的半径为 256 .
?
图170
类型四 圆中有关几何图形面积的问题
图7
7.(2023·十堰)如图7,在 Rt△???????????? 中,
∠????=90? , ????????=???????? ,点 ???? 在 ???????? 上,以点 ???? 为
圆心, ???????? 长为半径的半圆分别交 ???????? , ???????? , ????????
于点 ???? , ???? , ???? ,且点 ???? 是 ????????? 的中点.
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图7
图171
证明:如图171,连接 ???????? , ????????.
∵ ∠????=90? , ????????=???????? , ∴ ∠????????????=∠????=45? .
∵ ????????=????????, ∴ ∠????????????=∠????????????=45? .
∴ ∠????????????=90? .
∵ 点 ???? 是 ????????? 的中点, ∴ ∠????????????=∠????????????=12∠????????????=45? .
∴ ∠????????????=180??∠?????????????∠????=90? .
∴ ????????⊥????????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
图7
(2)若 ????????=2 ,求图中阴影部分的面积(结
果保留 π ).
?
解: ∵ ????????⊥???????? , ∠????=45? , ∴ △???????????? 是等
腰直角三角形.
设 ????????=????????=???? ,则 ????????=2???? , ∴ ????????=????+2????.
∵ ????????=2???????? , ∴ ????+2????=22+????.
解得 ????=2.
∴ ????阴影=????△?????????????????扇形????????????=12×2×2?45×π×22360=2?π2 .
?
图8
8.(2023·齐齐哈尔)如图8,在 Rt△???????????? 中,
∠????=90? , ???????? 平分 ∠???????????? 交 ???????? 于点 ???? ,点 ???? 是
斜边 ???????? 上一点,以 ???????? 为直径的 ⊙???? 经过点 ???? ,交
???????? 于点 ???? ,连接 ???????? .
?
(1)求证: ???????? 是 ⊙???? 的切线.
?
图8
图172
证明:如图172,连接 ????????.
∵ ????????=???????? , ∴ ∠????????????=∠????????????.
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????.
∴ ∠????????????=∠????????????.∴ ????????//????????.
∴ ∠????????????=∠????=90? .
∴ ????????⊥???????? 于点 ????.
∵ ???????? 是 ⊙???? 的半径, ∴ ???????? 是 ⊙???? 的切线.
?
(2)若 ????????=5 , tan?∠????????????=3 ,求图中阴影部分的面积(结果保留 π ).
?
图8
图172
解:如图172,连接 ???????? , ????????.
∵ ∠????=90? , tan?∠????????????=3 , ∴ ∠????????????=60? .
∴ ∠????????????=90??∠????????????=30? .
又 ∵ ????????=5 , ∴ ????????=2????????=10.
∵ ???????? 是 ⊙???? 的直径, ∴ ∠????????????=90?.
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=∠????????????=30?.
?
在 Rt△???????????? 中, ????????=10 ,cos?∠????????????=????????????????=32 , ∴ ????????=2033 .
∴ ????????=12????????=1033 .
∵ ???????? 平分 ∠???????????? , ∴ ∠????????????=2∠????????????=60?.
又 ∵ ????????=???????? , ∴ △???????????? 是等边三角形.
∴ ∠????????????=60? .
∵ ????????//???????? , ∴ ????△????????????=????△????????????.
∴ ????阴影=????扇形????????????=60×π×10332360=50π9 .
?
图172
同课章节目录
