5.1.2 垂线 教案 人教版数学七年级下册
文档属性
| 名称 | 5.1.2 垂线 教案 人教版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 104.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 10:42:55 | ||
图片预览

文档简介
5.1.2 垂线
※ 教学目标
1.知道垂直的概念,会用三角尺或量角器过一点画一条直线的垂线.
2.知道垂线的性质“在同一平面内,过一点有且只有一条直线与已知直线垂直”.
3.理解垂线段的概念,知道垂线段最短的性质,体会点到直线的距离的意义,并会度量点到直线的距离.
※ 重点难点
1.重点:两条直线互相垂直的概念、两个性质和画法,点到直线的距离的概念及其简单应用.
2.难点:垂线的性质及点到直线的距离.
※ 课前准备
三角尺、量角器、课件
一、 情境导入
如图,观察图形并填空:
(1)如图①所示,直线AB与直线CD相交于点O,其中对顶角有__2__对,分别为__∠AOD和∠BOC,∠AOC和∠BOD__;邻补角有__4__对,分别为__∠AOD和∠AOC,∠AOC和∠BOC,∠BOC和∠BOD,∠AOD和∠BOD__.
(2)图①中,当直线CD绕点O逆时针旋转到∠AOC=90°时(如图②),你能求出其他角的度数吗?此图形有什么特点?此时两直线有什么关系?
二、探究新知
>> 活动1: 垂直的定义是什么?如何表示垂直?
(1)定义:两条直线相交,所成四个角中有一个角是__90°__时,我们称这两条直线__互相垂直__,其中一条直线是另一条的__垂线__,它们的交点叫做__垂足__.
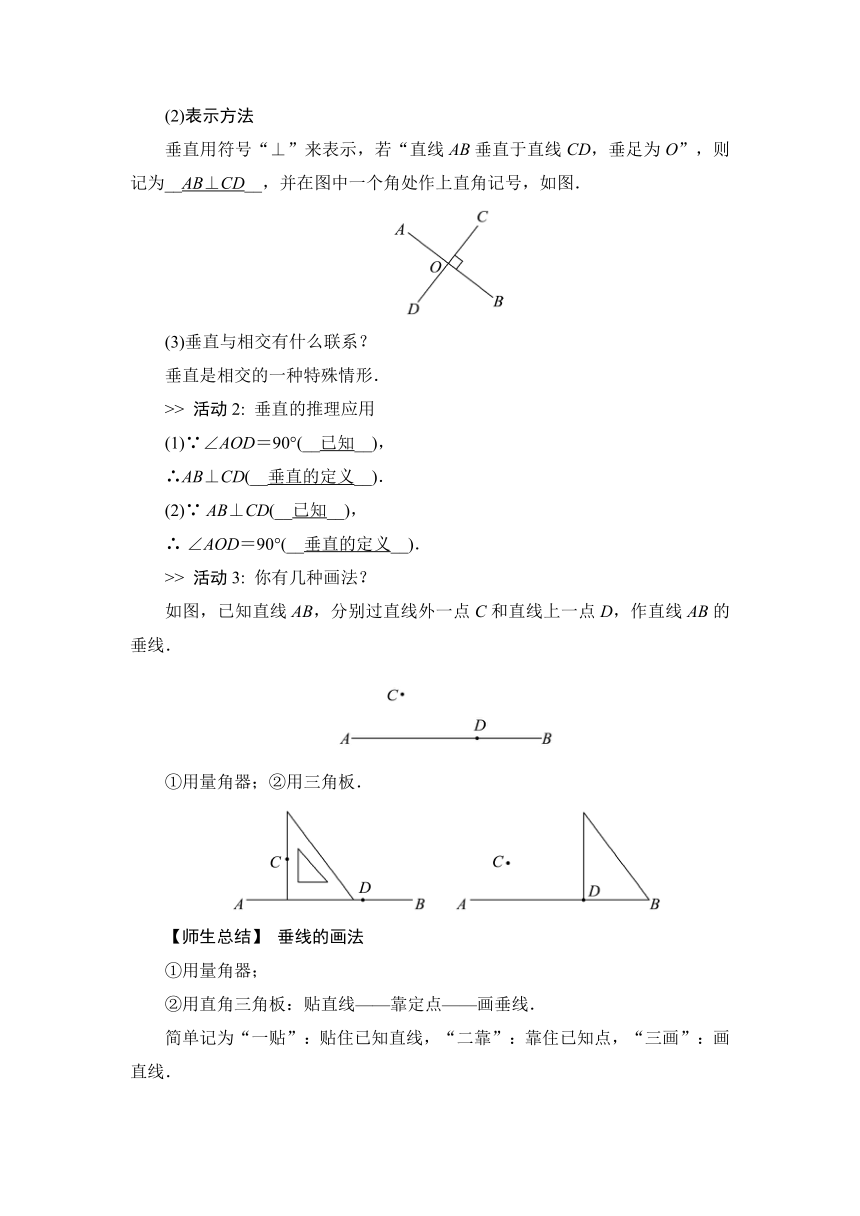
(2)表示方法
垂直用符号“⊥”来表示,若“直线AB垂直于直线CD,垂足为O”,则记为__AB⊥CD__,并在图中一个角处作上直角记号,如图.
(3)垂直与相交有什么联系?
垂直是相交的一种特殊情形.
>> 活动2: 垂直的推理应用
(1)∵∠AOD=90°(__已知__),
∴AB⊥CD(__垂直的定义__).
(2)∵ AB⊥CD(__已知__),
∴ ∠AOD=90°(__垂直的定义__).
>> 活动3: 你有几种画法?
如图,已知直线AB,分别过直线外一点C和直线上一点D,作直线AB的垂线.
①用量角器;②用三角板.
【师生总结】 垂线的画法
①用量角器;
②用直角三角板:贴直线——靠定点——画垂线.
简单记为“一贴”:贴住已知直线,“二靠”:靠住已知点,“三画”:画直线.
>> 活动4: 活动3中的垂线可以作出几条?你发现什么结论?
【师生总结】 在同一平面内,过一点有且只有一条直线与已知直线垂直.
>> 变式小练
画图操作:
①画出直线l及l外一点P;
②过点P作PO⊥l,垂足为O;
③点A1,A2,A3,…在l上,连接PA1,PA2,PA3,….
>> 活动5: 在活动4变式小练的图中,如何比较PO,PA1,PA2,PA3的长短呢?
a.叠合法;b.度量法.
归纳:连接直线外一点与直线上各点的所有线段中,垂线段最短.简称垂线段最短.
结合图形,理解垂线段PO;PO⊥l,∠POA1=90°,O为垂足.
【师生总结】 点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
师生活动:
①明晰学情:关注学生对概念的理解及垂线性质的认识.
②差异指导:巡视全班,及时对学习有困难的学生引导和点拨.
③生生互助:小组交流讨论,相互释疑,形成共识.
三、典例精讲
>> 例: 如图,在给出的图形上,完成下列作图:
(1)作出点A到直线BC的垂线段AD,并量出点A到直线BC的距离;
(2)过点B作AC的垂线,垂足为E,过点C作AB的垂线,垂足为F;
(3)延长DA,BE,CF,你能发现什么有趣的结论?
分析:利用三角板画垂线,“一贴”,即直角三角板的一直角边贴在已知直线上;“二靠”,即三角板的另一直角边经过已知点;“三画”,即过已知点的直角边画垂线.画一条线段的垂线,就是画这条线段所在直线的垂线,垂足可能在线段或线段的延长线上.
解:(1)(2)的作图如图所示.
(3)直线DA,BE,CF相交于同一点.
四、 巩固练习
1.判断题.
(1)两条直线互相垂直,则所有的邻补角都相等.( √ )
(2)一条直线不可能与两条相交直线都垂直.( × )
(3)两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.( × )
(4)两条直线相交有一组对顶角互补,那么这两条直线互相垂直.( √ )
2.如图,点A,B,C在直线l上,PB⊥l,PA=6 cm,PB=5 cm,PC=7 cm,则点P到直线l的距离是__5__ cm.
五、 课堂小结
1.垂线
2.点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
3.垂线的性质
(1)垂线的唯一性;(2)垂线段最短.
【教学反思】
教学时我让学生通过观察两根木条,其中一根固定,另一根转动后交角变化得出垂直的定义,比较直观,当充分理解垂直的定义后,在此基础上我又让学生在纸上随意画一条直线,要求经过直线外任意一点画垂线,他们的问题来了,画成线段?射线?还是直线?而在画的时候又有了很多的麻烦,先画了过要求的点到直线的射线,还要延长,还要作垂直标志.对于不够熟练的学生在画图的过程中就很容易出现错误.
因此我要求学生采用不同的工具(量角器或者三角板)尝试比较,有学生马上就有自己的见解了,让三角板的一条直角边和直线重合,三角板的另一条直角边过已知点,就可一次画好.以前教学时总是强调的问题学生通过自己的尝试效果就好很多,同时还一起验证了画出的直线和已知直线是否垂直.练习中错误也少了,因此几何的教学中,老师多给学生尝试动手、动脑的机会胜过自己的反复说教.
※ 教学目标
1.知道垂直的概念,会用三角尺或量角器过一点画一条直线的垂线.
2.知道垂线的性质“在同一平面内,过一点有且只有一条直线与已知直线垂直”.
3.理解垂线段的概念,知道垂线段最短的性质,体会点到直线的距离的意义,并会度量点到直线的距离.
※ 重点难点
1.重点:两条直线互相垂直的概念、两个性质和画法,点到直线的距离的概念及其简单应用.
2.难点:垂线的性质及点到直线的距离.
※ 课前准备
三角尺、量角器、课件
一、 情境导入
如图,观察图形并填空:
(1)如图①所示,直线AB与直线CD相交于点O,其中对顶角有__2__对,分别为__∠AOD和∠BOC,∠AOC和∠BOD__;邻补角有__4__对,分别为__∠AOD和∠AOC,∠AOC和∠BOC,∠BOC和∠BOD,∠AOD和∠BOD__.
(2)图①中,当直线CD绕点O逆时针旋转到∠AOC=90°时(如图②),你能求出其他角的度数吗?此图形有什么特点?此时两直线有什么关系?
二、探究新知
>> 活动1: 垂直的定义是什么?如何表示垂直?
(1)定义:两条直线相交,所成四个角中有一个角是__90°__时,我们称这两条直线__互相垂直__,其中一条直线是另一条的__垂线__,它们的交点叫做__垂足__.
(2)表示方法
垂直用符号“⊥”来表示,若“直线AB垂直于直线CD,垂足为O”,则记为__AB⊥CD__,并在图中一个角处作上直角记号,如图.
(3)垂直与相交有什么联系?
垂直是相交的一种特殊情形.
>> 活动2: 垂直的推理应用
(1)∵∠AOD=90°(__已知__),
∴AB⊥CD(__垂直的定义__).
(2)∵ AB⊥CD(__已知__),
∴ ∠AOD=90°(__垂直的定义__).
>> 活动3: 你有几种画法?
如图,已知直线AB,分别过直线外一点C和直线上一点D,作直线AB的垂线.
①用量角器;②用三角板.
【师生总结】 垂线的画法
①用量角器;
②用直角三角板:贴直线——靠定点——画垂线.
简单记为“一贴”:贴住已知直线,“二靠”:靠住已知点,“三画”:画直线.
>> 活动4: 活动3中的垂线可以作出几条?你发现什么结论?
【师生总结】 在同一平面内,过一点有且只有一条直线与已知直线垂直.
>> 变式小练
画图操作:
①画出直线l及l外一点P;
②过点P作PO⊥l,垂足为O;
③点A1,A2,A3,…在l上,连接PA1,PA2,PA3,….
>> 活动5: 在活动4变式小练的图中,如何比较PO,PA1,PA2,PA3的长短呢?
a.叠合法;b.度量法.
归纳:连接直线外一点与直线上各点的所有线段中,垂线段最短.简称垂线段最短.
结合图形,理解垂线段PO;PO⊥l,∠POA1=90°,O为垂足.
【师生总结】 点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
师生活动:
①明晰学情:关注学生对概念的理解及垂线性质的认识.
②差异指导:巡视全班,及时对学习有困难的学生引导和点拨.
③生生互助:小组交流讨论,相互释疑,形成共识.
三、典例精讲
>> 例: 如图,在给出的图形上,完成下列作图:
(1)作出点A到直线BC的垂线段AD,并量出点A到直线BC的距离;
(2)过点B作AC的垂线,垂足为E,过点C作AB的垂线,垂足为F;
(3)延长DA,BE,CF,你能发现什么有趣的结论?
分析:利用三角板画垂线,“一贴”,即直角三角板的一直角边贴在已知直线上;“二靠”,即三角板的另一直角边经过已知点;“三画”,即过已知点的直角边画垂线.画一条线段的垂线,就是画这条线段所在直线的垂线,垂足可能在线段或线段的延长线上.
解:(1)(2)的作图如图所示.
(3)直线DA,BE,CF相交于同一点.
四、 巩固练习
1.判断题.
(1)两条直线互相垂直,则所有的邻补角都相等.( √ )
(2)一条直线不可能与两条相交直线都垂直.( × )
(3)两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.( × )
(4)两条直线相交有一组对顶角互补,那么这两条直线互相垂直.( √ )
2.如图,点A,B,C在直线l上,PB⊥l,PA=6 cm,PB=5 cm,PC=7 cm,则点P到直线l的距离是__5__ cm.
五、 课堂小结
1.垂线
2.点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
3.垂线的性质
(1)垂线的唯一性;(2)垂线段最短.
【教学反思】
教学时我让学生通过观察两根木条,其中一根固定,另一根转动后交角变化得出垂直的定义,比较直观,当充分理解垂直的定义后,在此基础上我又让学生在纸上随意画一条直线,要求经过直线外任意一点画垂线,他们的问题来了,画成线段?射线?还是直线?而在画的时候又有了很多的麻烦,先画了过要求的点到直线的射线,还要延长,还要作垂直标志.对于不够熟练的学生在画图的过程中就很容易出现错误.
因此我要求学生采用不同的工具(量角器或者三角板)尝试比较,有学生马上就有自己的见解了,让三角板的一条直角边和直线重合,三角板的另一条直角边过已知点,就可一次画好.以前教学时总是强调的问题学生通过自己的尝试效果就好很多,同时还一起验证了画出的直线和已知直线是否垂直.练习中错误也少了,因此几何的教学中,老师多给学生尝试动手、动脑的机会胜过自己的反复说教.
