第十九章一次函数 单元测试(含答案) 2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 第十九章一次函数 单元测试(含答案) 2023-2024学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 521.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 23:48:34 | ||
图片预览




文档简介
第十九章一次函数(单元测试)2023-2024学年八年级下册数学人教版
一、单选题(共10小题,满分40分)
1.某种水果的购买金额(元)与购买量(千克)之间的函数图象如图所示,当购买该种水果9千克时,需要付款( )
A.120元 B.140元 C.170元 D.180元
2.一次函数的图象与y轴的交点坐标是( )
A.(4,0) B.(0,4) C.(2,0) D.(0,2)
3.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与时间t(h)的函数图象如图所示.根据图象得出下列结论,其中错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.妈妈比小亮提前0.5 h到达姥姥家
C.妈妈在距家12 km处追上小亮
D.9:30妈妈追上小亮
4.学习完“一次函数”,王老师出了一道题:已知,且,则一次函数的图象大致是( )
A. B. C. D.
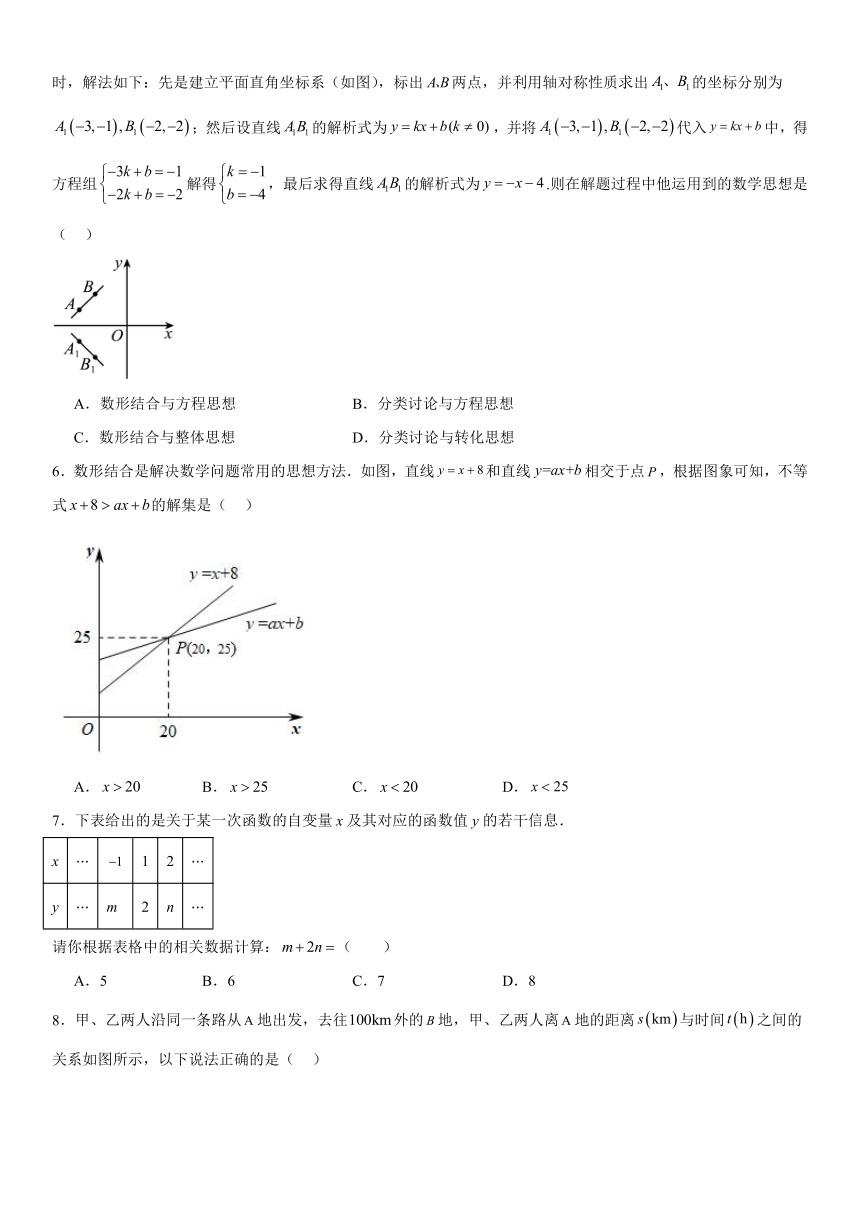
5.开元同学在解决问题“已知两点的坐标为,求直线关于轴的对称直线的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出两点,并利用轴对称性质求出的坐标分别为;然后设直线的解析式为,并将代入中,得方程组解得,最后求得直线的解析式为.则在解题过程中他运用到的数学思想是( )
A.数形结合与方程思想 B.分类讨论与方程思想
C.数形结合与整体思想 D.分类讨论与转化思想
6.数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点,根据图象可知,不等式的解集是( )
A. B. C. D.
7.下表给出的是关于某一次函数的自变量x及其对应的函数值y的若干信息.
x 1 2
y m 2 n
请你根据表格中的相关数据计算:( )
A.5 B.6 C.7 D.8
8.甲、乙两人沿同一条路从地出发,去往外的地,甲、乙两人离地的距离与时间之间的关系如图所示,以下说法正确的是( )
A.甲出发后两人第一次相遇 B.甲的速度是
C.甲、乙同时到达地 D.乙出发或或时,甲、乙两人相距
9.已知直线y1=2x与直线y2=﹣2x+4相交于点A.以下结论:
①点A的坐标为A(1,2);②当x=1时,两个函数值相等:
③当x<1时,y1<y2; ④直线y1=2x与直线y2=﹣2x+4在平面直角坐标系中的位置关系是平行.其中正确的个数有( )个.
A.4 B.3 C.2 D.1
10.甲,乙两车在笔直的公路上行驶,乙车从之间的地出发,到达终点地停止行驶,甲车从起点地与乙车同时出发,到达地休息半小时后,立即以另一速度返回地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车相距的路程(千米)与乙车行驶的时间(小时)之间的关系如图所示,下列说法错误的是( )
A.乙车行驶的速度为每小时40千米 B.甲车到达地的时间为7小时
C.甲车返回地比乙车到地时间晚3小时 D.甲车全程共行驶了840千米
二、填空题(共8小题,满分32分)
11.已知a,b是非零实数,若关于x的不等式,所解得,则一次函数的图像必经过点 .
12.已知直线和图象上部分点的横坐标和纵坐标如下表所示,则关于的方程的解是 .
x 0 1 2
8 5 2 -1
0 1 2 3
13.已知一个长方体的木箱高为80厘米,底面的长比宽多10厘米,则这个长方体的体积(立方厘米)与长方体的宽(厘米)之间的函数解析式是 .
14.火车“动车组”以250千米/时的速度行驶,则行驶的路程s(千米)与行驶时间t(小时)之间的函数关系式是 ,它是 函数.(填“正比例”或“一次”)
15.在平面直角坐标系中,点M(m+2n,-3)和N(-m-n,6),点M与点N关于直线l(直线l上各点的横纵坐标相等)对称,则m与n的数量关系为 .
16.甲、乙两车分别从两地同时相向匀速行驶,当乙车到达地后,继续保持原速向远离地的方向行驶,而甲车到达地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达地,设两车行驶的时间为,两车之间的距离为,与之间的函数关系如图所示,则两地相距 千米.
17.如图,直线与x轴,y轴分别相交于点A和点B,若点P(1,m)使得PA+PB的值最小,点Q(1,n)使得的值最大,则 .
18.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是 米/分钟.
三、解答题(共6小题,每题8分,满分48分)
19.小亮家与学校之间有一商店,小亮骑自行车由家匀速行驶去学校,然后在校学习6小时.最后放学骑车匀速回家(上学与放学均不在商店停留).折线OABC表示小亮离家的距离y(km)与离家的时间x(h)之间的函数关系.根据已上信息,解答下列问题:
(1)小亮上学的速度为 km/h,放学回家的速度为 km/h;
(2)求线段BC所表示的y与x之间的函数关系;
(3)如果小亮两次经过商店的时间间隔为7.2小时,那么商店离小亮家多远?
20.有一科技小组进行机器人行走性能测验,在测验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时同时到达C点,甲机器人前3分钟以的速度行走,乙机器人始终以的速度行走,如图是甲、乙两机器人之间的距离与它们的行走时间之间的函数图象,请结合图象,回答下列问题.
(1)A、B两点之间的距离是_________,A、C两点之间的距离是_________,__________;
(2)求线段所在直线的函数表达式;__________.
(3)设线段轴.
①当时,甲机器人的速度为__________.
②直接写出两机器人出发多长时间相距.
21.2023年2月15日,“二十世纪初中国古文献四大发现展”开幕式在国家典籍博物馆举行,本次展览是迄今为止展品规模最大、等级最高的一次古代文献展.为了透过古文献近距离感受源远流长、博大精深的中华优秀传统文化,某校组织学生从学校出发前往国家典籍博物馆参观,返回途中遇到车辆故障,修好车后按原速度继续行驶,直至到达学校.学生距学校的距离y()与行驶时间x(h)之间的关系如图所示,根据图中信息解答下列问题:
(1)求段所对应的函数表达式;
(2)出发多久后,学生距学校的距离为?
22.如图,直线经过点、和点,且点的横坐标为,点为线段的中点.
(1)求直线的解析式;
(2)若点为线段上的一个动点,当的值最小时,求出点坐标.
23.如图,平面直角坐标系中,线段的端点为,.
(1)求所在直线的解析式;
(2)某同学设计了一个动画:在函数(,)中,分别输入m和n的值,可得到射线,其中.当时,会从C处弹出一个光点P,并沿飞行;当时,只发出射线而无光点弹出,
①若有光点P弹出,试推算m,n应满足的数量关系;
②当有光点P弹出,并击中线段上的整点(横、纵坐标都是整数)时,线段就会发光.直接写出正整数m的值.
24.如图1,在平面直角坐标系中,直线与x轴、y轴分别交于B、C两点,点A为y轴上一点,直线的解析式为.
(1)请直接写出点A、B、C的坐标:A_______、B_______、C_______;
(2)如图2,点P为线段上一点,若,求出点P的坐标;
(3)如图3,点D是直线上的动点,以为边顺时针方向作正方形,连接,若,求点F坐标.
参考答案:
1.B
2.B
3.D
4.D
5.A
6.A
7.B
8.D
9.B
10.D
11.(-2,-1)
12.
13.
14. s=250t 正比例
15.
16.300
17.
18.80
19.(1)5km/h,1km/h;(2)y=﹣x+9.6(6.6≤x≤9.6);(3)商店离家2km
20.(1)70,490,95;(2)y=35x-70;(3)①60;②1.2分钟或2.8分钟或4.6分钟
21.(1)
(2)和
22.(1)
(2)点坐标为
23.(1)
(2)①;②或
24.(1),,
(2)
(3),
一、单选题(共10小题,满分40分)
1.某种水果的购买金额(元)与购买量(千克)之间的函数图象如图所示,当购买该种水果9千克时,需要付款( )
A.120元 B.140元 C.170元 D.180元
2.一次函数的图象与y轴的交点坐标是( )
A.(4,0) B.(0,4) C.(2,0) D.(0,2)
3.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与时间t(h)的函数图象如图所示.根据图象得出下列结论,其中错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.妈妈比小亮提前0.5 h到达姥姥家
C.妈妈在距家12 km处追上小亮
D.9:30妈妈追上小亮
4.学习完“一次函数”,王老师出了一道题:已知,且,则一次函数的图象大致是( )
A. B. C. D.
5.开元同学在解决问题“已知两点的坐标为,求直线关于轴的对称直线的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出两点,并利用轴对称性质求出的坐标分别为;然后设直线的解析式为,并将代入中,得方程组解得,最后求得直线的解析式为.则在解题过程中他运用到的数学思想是( )
A.数形结合与方程思想 B.分类讨论与方程思想
C.数形结合与整体思想 D.分类讨论与转化思想
6.数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点,根据图象可知,不等式的解集是( )
A. B. C. D.
7.下表给出的是关于某一次函数的自变量x及其对应的函数值y的若干信息.
x 1 2
y m 2 n
请你根据表格中的相关数据计算:( )
A.5 B.6 C.7 D.8
8.甲、乙两人沿同一条路从地出发,去往外的地,甲、乙两人离地的距离与时间之间的关系如图所示,以下说法正确的是( )
A.甲出发后两人第一次相遇 B.甲的速度是
C.甲、乙同时到达地 D.乙出发或或时,甲、乙两人相距
9.已知直线y1=2x与直线y2=﹣2x+4相交于点A.以下结论:
①点A的坐标为A(1,2);②当x=1时,两个函数值相等:
③当x<1时,y1<y2; ④直线y1=2x与直线y2=﹣2x+4在平面直角坐标系中的位置关系是平行.其中正确的个数有( )个.
A.4 B.3 C.2 D.1
10.甲,乙两车在笔直的公路上行驶,乙车从之间的地出发,到达终点地停止行驶,甲车从起点地与乙车同时出发,到达地休息半小时后,立即以另一速度返回地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车相距的路程(千米)与乙车行驶的时间(小时)之间的关系如图所示,下列说法错误的是( )
A.乙车行驶的速度为每小时40千米 B.甲车到达地的时间为7小时
C.甲车返回地比乙车到地时间晚3小时 D.甲车全程共行驶了840千米
二、填空题(共8小题,满分32分)
11.已知a,b是非零实数,若关于x的不等式,所解得,则一次函数的图像必经过点 .
12.已知直线和图象上部分点的横坐标和纵坐标如下表所示,则关于的方程的解是 .
x 0 1 2
8 5 2 -1
0 1 2 3
13.已知一个长方体的木箱高为80厘米,底面的长比宽多10厘米,则这个长方体的体积(立方厘米)与长方体的宽(厘米)之间的函数解析式是 .
14.火车“动车组”以250千米/时的速度行驶,则行驶的路程s(千米)与行驶时间t(小时)之间的函数关系式是 ,它是 函数.(填“正比例”或“一次”)
15.在平面直角坐标系中,点M(m+2n,-3)和N(-m-n,6),点M与点N关于直线l(直线l上各点的横纵坐标相等)对称,则m与n的数量关系为 .
16.甲、乙两车分别从两地同时相向匀速行驶,当乙车到达地后,继续保持原速向远离地的方向行驶,而甲车到达地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达地,设两车行驶的时间为,两车之间的距离为,与之间的函数关系如图所示,则两地相距 千米.
17.如图,直线与x轴,y轴分别相交于点A和点B,若点P(1,m)使得PA+PB的值最小,点Q(1,n)使得的值最大,则 .
18.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是 米/分钟.
三、解答题(共6小题,每题8分,满分48分)
19.小亮家与学校之间有一商店,小亮骑自行车由家匀速行驶去学校,然后在校学习6小时.最后放学骑车匀速回家(上学与放学均不在商店停留).折线OABC表示小亮离家的距离y(km)与离家的时间x(h)之间的函数关系.根据已上信息,解答下列问题:
(1)小亮上学的速度为 km/h,放学回家的速度为 km/h;
(2)求线段BC所表示的y与x之间的函数关系;
(3)如果小亮两次经过商店的时间间隔为7.2小时,那么商店离小亮家多远?
20.有一科技小组进行机器人行走性能测验,在测验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时同时到达C点,甲机器人前3分钟以的速度行走,乙机器人始终以的速度行走,如图是甲、乙两机器人之间的距离与它们的行走时间之间的函数图象,请结合图象,回答下列问题.
(1)A、B两点之间的距离是_________,A、C两点之间的距离是_________,__________;
(2)求线段所在直线的函数表达式;__________.
(3)设线段轴.
①当时,甲机器人的速度为__________.
②直接写出两机器人出发多长时间相距.
21.2023年2月15日,“二十世纪初中国古文献四大发现展”开幕式在国家典籍博物馆举行,本次展览是迄今为止展品规模最大、等级最高的一次古代文献展.为了透过古文献近距离感受源远流长、博大精深的中华优秀传统文化,某校组织学生从学校出发前往国家典籍博物馆参观,返回途中遇到车辆故障,修好车后按原速度继续行驶,直至到达学校.学生距学校的距离y()与行驶时间x(h)之间的关系如图所示,根据图中信息解答下列问题:
(1)求段所对应的函数表达式;
(2)出发多久后,学生距学校的距离为?
22.如图,直线经过点、和点,且点的横坐标为,点为线段的中点.
(1)求直线的解析式;
(2)若点为线段上的一个动点,当的值最小时,求出点坐标.
23.如图,平面直角坐标系中,线段的端点为,.
(1)求所在直线的解析式;
(2)某同学设计了一个动画:在函数(,)中,分别输入m和n的值,可得到射线,其中.当时,会从C处弹出一个光点P,并沿飞行;当时,只发出射线而无光点弹出,
①若有光点P弹出,试推算m,n应满足的数量关系;
②当有光点P弹出,并击中线段上的整点(横、纵坐标都是整数)时,线段就会发光.直接写出正整数m的值.
24.如图1,在平面直角坐标系中,直线与x轴、y轴分别交于B、C两点,点A为y轴上一点,直线的解析式为.
(1)请直接写出点A、B、C的坐标:A_______、B_______、C_______;
(2)如图2,点P为线段上一点,若,求出点P的坐标;
(3)如图3,点D是直线上的动点,以为边顺时针方向作正方形,连接,若,求点F坐标.
参考答案:
1.B
2.B
3.D
4.D
5.A
6.A
7.B
8.D
9.B
10.D
11.(-2,-1)
12.
13.
14. s=250t 正比例
15.
16.300
17.
18.80
19.(1)5km/h,1km/h;(2)y=﹣x+9.6(6.6≤x≤9.6);(3)商店离家2km
20.(1)70,490,95;(2)y=35x-70;(3)①60;②1.2分钟或2.8分钟或4.6分钟
21.(1)
(2)和
22.(1)
(2)点坐标为
23.(1)
(2)①;②或
24.(1),,
(2)
(3),
