微专题(九) 判定切线的常见方法 课件(共18张PPT) 2024中考数学总复习专题突破
文档属性
| 名称 | 微专题(九) 判定切线的常见方法 课件(共18张PPT) 2024中考数学总复习专题突破 |  | |
| 格式 | pptx | ||
| 文件大小 | 956.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 23:34:34 | ||
图片预览




文档简介
(共18张PPT)
复习讲义
第一篇 基础过关
第六部分 圆
微专题(九) 判定切线的常见方法
方法一 作半径,证垂直
方法解读
判定一条直线是圆的切线,当已知直线与圆有公共点时,常通过
“证垂直”进行判断.一般辅助线的作法是:连接圆心与公共点,证明所作
半径垂直于已知直线,即“连半径,证垂直,得切线”.
方法应用
图1
1.如图1,线段 是 的直径,延长 至点 ,
使 ,点 是线段 的中点, 交
于点 ,连接 .求证: 是 的切线.
小锦囊 根据切线的判定定理,只要证明 的半径 即
可.利用圆的性质、垂直平分线的性质和线段的等量关系,可证明
是等边三角形,再证明 即可.
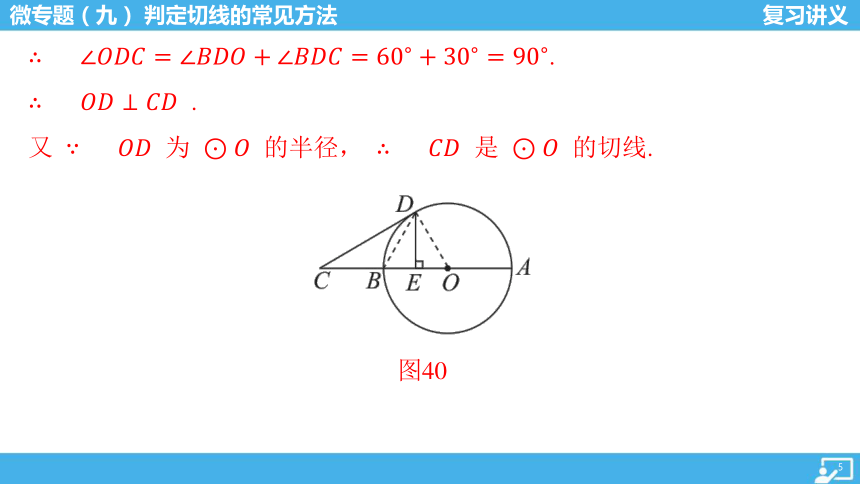
图40
证明:如图40,连接 ,
点 是线段 的中点, 交 于点 , , 是 的垂直平分线.
.
又 ,
是等边三角形.
.
,且 为 的外角,
.
.
.
又 为 的半径, 是 的切线.
图40
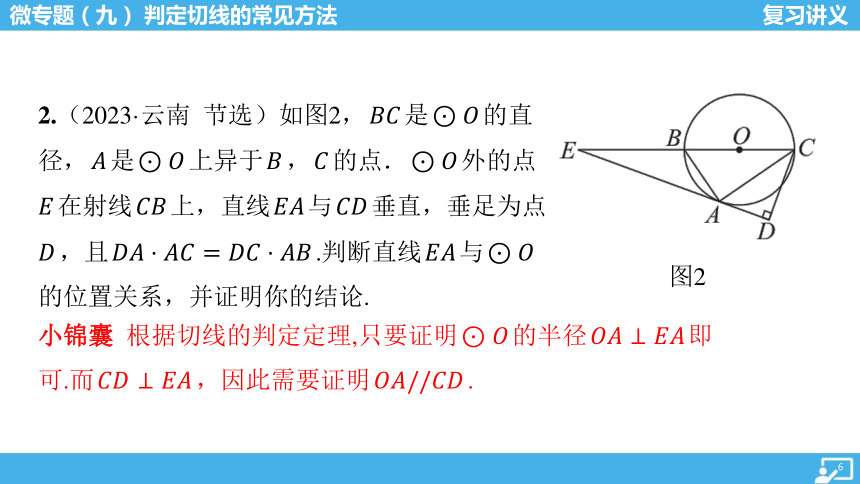
图2
2.(2023·云南 节选)如图2, 是 的直
径, 是 上异于 , 的点. 外的点
在射线 上,直线 与 垂直,垂足为点
,且 .判断直线 与
的位置关系,并证明你的结论.
小锦囊 根据切线的判定定理,只要证明 的半径 即
可.而 ,因此需要证明 .
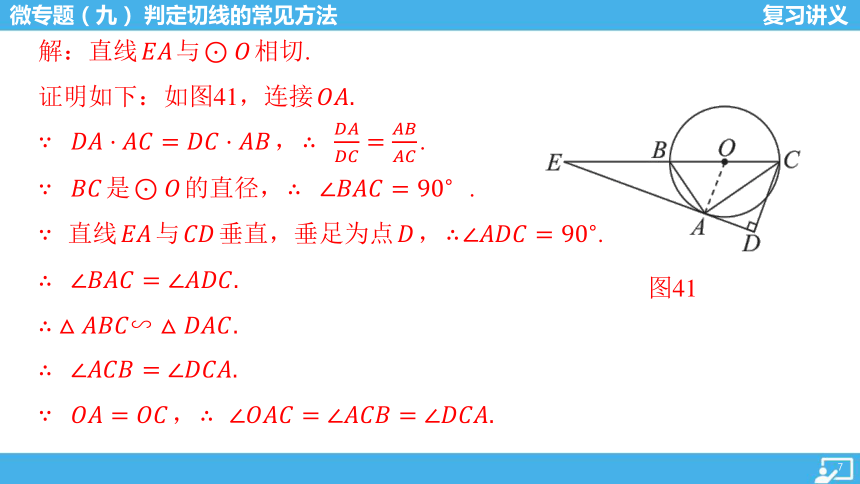
图41
解:直线 与 相切.
证明如下:如图41,连接
, .
是 的直径, .
直线 与 垂直,垂足为点 , .
,
.
.
又 为 的半径, 与 相切.
图41
方法二 作垂直,证半径
方法解读
判定一条直线是圆的切线,当已知条件没有指出直线与圆有公共点
时,常通过“证半径”进行判断.一般辅助线的作法是:过圆心作已知直线
的垂线段,证明垂线段的长等于半径长,即“作垂直,证半径,得切线”.
方法应用
图3
3.如图3,在 中, , 是 边的中
点, 与 相切于点 ,连接 .求证:
是 的切线.
小锦囊 根据切线的判定定理,只要证明由点 向 所作的垂线
段 是 的半径,就可以了.而 是 的半径,因此需要证明
.
图42
证明:如图42,连接 , ,过点 作 ,垂足为点
与 相切于点 , ,即 .
, .
, 是 边的中点, .
又 ,
,即圆心 到直线 的距离 等于 的半径
是 的切线.
学习至此,请完成微专题练习(九) (第282页)
微专题练习(九)
判定切线的常见方法
方法一 作半径,证垂直
图1
1.(2023·江西 改编)如图1,在 中,
.以 为直径的 与 相交于点 ,
为 上一点,且 , .求
证: 是 的切线.
图68
证明:如图68,连接
, .
.
, .
又 , .
.
为 的直径, 是 的切线.
图2
2.(2023·达州 节选)如图2, 内接于 ,
, 是 延长线上的一点, .
求证: 是 的切线.
证明:如图69,连接
,
,
, .
.
图69
图69
.
,即
为 的半径, 是 的切线.
方法二 作垂直,证半径
图3
3.如图3,在 中, , 的平分线交 于点 .以点 为圆心, 长为半径作 .求证:
与 相切.
图70
证明:如图70,过点 作 于点
, .
又 平分 ,
为 的半径.
与 相切.
图4
4.如图4,在 中, , , ,以 为圆心,4为半径作 .求证: 是 的切线.
图71
证明:如图71,作 于点
, .
在 中,
, .
又 的半径为4, 为 的半径.
是 的切线.
复习讲义
第一篇 基础过关
第六部分 圆
微专题(九) 判定切线的常见方法
方法一 作半径,证垂直
方法解读
判定一条直线是圆的切线,当已知直线与圆有公共点时,常通过
“证垂直”进行判断.一般辅助线的作法是:连接圆心与公共点,证明所作
半径垂直于已知直线,即“连半径,证垂直,得切线”.
方法应用
图1
1.如图1,线段 是 的直径,延长 至点 ,
使 ,点 是线段 的中点, 交
于点 ,连接 .求证: 是 的切线.
小锦囊 根据切线的判定定理,只要证明 的半径 即
可.利用圆的性质、垂直平分线的性质和线段的等量关系,可证明
是等边三角形,再证明 即可.
图40
证明:如图40,连接 ,
点 是线段 的中点, 交 于点 , , 是 的垂直平分线.
.
又 ,
是等边三角形.
.
,且 为 的外角,
.
.
.
又 为 的半径, 是 的切线.
图40
图2
2.(2023·云南 节选)如图2, 是 的直
径, 是 上异于 , 的点. 外的点
在射线 上,直线 与 垂直,垂足为点
,且 .判断直线 与
的位置关系,并证明你的结论.
小锦囊 根据切线的判定定理,只要证明 的半径 即
可.而 ,因此需要证明 .
图41
解:直线 与 相切.
证明如下:如图41,连接
, .
是 的直径, .
直线 与 垂直,垂足为点 , .
,
.
.
又 为 的半径, 与 相切.
图41
方法二 作垂直,证半径
方法解读
判定一条直线是圆的切线,当已知条件没有指出直线与圆有公共点
时,常通过“证半径”进行判断.一般辅助线的作法是:过圆心作已知直线
的垂线段,证明垂线段的长等于半径长,即“作垂直,证半径,得切线”.
方法应用
图3
3.如图3,在 中, , 是 边的中
点, 与 相切于点 ,连接 .求证:
是 的切线.
小锦囊 根据切线的判定定理,只要证明由点 向 所作的垂线
段 是 的半径,就可以了.而 是 的半径,因此需要证明
.
图42
证明:如图42,连接 , ,过点 作 ,垂足为点
与 相切于点 , ,即 .
, .
, 是 边的中点, .
又 ,
,即圆心 到直线 的距离 等于 的半径
是 的切线.
学习至此,请完成微专题练习(九) (第282页)
微专题练习(九)
判定切线的常见方法
方法一 作半径,证垂直
图1
1.(2023·江西 改编)如图1,在 中,
.以 为直径的 与 相交于点 ,
为 上一点,且 , .求
证: 是 的切线.
图68
证明:如图68,连接
, .
.
, .
又 , .
.
为 的直径, 是 的切线.
图2
2.(2023·达州 节选)如图2, 内接于 ,
, 是 延长线上的一点, .
求证: 是 的切线.
证明:如图69,连接
,
,
, .
.
图69
图69
.
,即
为 的半径, 是 的切线.
方法二 作垂直,证半径
图3
3.如图3,在 中, , 的平分线交 于点 .以点 为圆心, 长为半径作 .求证:
与 相切.
图70
证明:如图70,过点 作 于点
, .
又 平分 ,
为 的半径.
与 相切.
图4
4.如图4,在 中, , , ,以 为圆心,4为半径作 .求证: 是 的切线.
图71
证明:如图71,作 于点
, .
在 中,
, .
又 的半径为4, 为 的半径.
是 的切线.
同课章节目录
